输入饱和下的AUV水平面轨迹跟踪滑模控制

闫方正,靳华伟,2

(安徽理工大学 1.机械工程学院;2.安徽省矿山智能装备与技术重点实验室,安徽 淮南 232001)

二十一世纪是海洋的世纪,全球海洋面积占地球总面积的71%,世界各国都把目光转向资源丰富的海洋[1]。中国幅员辽阔,管辖海域面积较广,其海洋资源种类丰富,包括生物资源、油气资源、海底固体矿产资源等。要开发海洋资源,水下航行器的应用必不可少[2-3]。

自主水下航行器(Autonomous Underwater Vehicle, AUV),拥有体积小、灵活性高、稳定性强、续航能力强、精确度高的优势,没有线缆的约束,能够在大范围恶劣的水下环境中工作。AUV的轨迹跟踪控制是指预先规划航线,确保AUV从初始位置进入航线,并沿着预先规划的航线到达目的地,在此过程中能够一直保持稳定[4]。

针对AUV的轨迹跟踪问题,杨泽文[5]针对AUV轨迹跟踪的响应速度较慢、系统严重抖振、运动轨迹与期望轨迹误差较大等问题,设计了一种欠驱动AUV水平面轨迹跟踪控制器。Kong Shihan[6]考虑轨迹跟踪任务中的欠驱动特性、速度约束和集总扰动,设计了一种由模型预测调速器的控制器组成的控制方案。Gao ZY[7]提出了一种有限时间和固定时间反推控制方案,AUV可以在所有信号均有界的情况下跟踪给定的航向,并且跟踪误差在稳定时间内收敛到零附近。

针对AUV的轨迹跟踪中出现的扰动问题,Ruikun Xu[8]研究了存在参数不确定性、未知干扰和输入饱和的情况下,AUV的姿态跟踪控制的问题。严浙平[9]在考虑时变外界干扰条件下,设计在出时变干扰下的欠驱动AUV水平面轨迹跟踪控制器;李鑫滨[10]针对欠驱动AUV的水平面轨迹跟踪问题,考虑了外界干扰和输入受限的情况,提出了基于非线性干扰观测器和径向基函数神经网络的滑模控制器;王金强[11]针对欠驱动AUV的三维路径跟踪问题,考虑参数不确定性和外界未知干扰,设计了一种基于神经网络的反步滑模控制器;刘丽萍[12]考虑环境中的海流速度对AUV的影响,设计了海流观测器对其进行估计,并基于自适应理论设计了AUV的反演滑模轨迹跟踪控制器。

针对AUV的轨迹跟踪中出现的输入饱和问题,Jiangshuai Huang[13]考虑输入饱和下欠驱动船舶的全局跟踪控制问题,设计出一种有限时间偏航控制器。Zhu Guibing[14]同时考虑未知参数、未知有界干扰和输入饱和,提出了全局稳定鲁棒自适应轨迹跟踪控制方案。Khoshnam Shojaei[15]通过在控制器的设计中使用饱和函数和神经网络,降低了制动器饱和的风险,补偿饱和非线性、不确定参数、未建模动态和波浪、风和洋流引起的环境干扰。

综上所述,针对AUV控制研究中的执行器输入饱和及不确定性扰动等问题,大多数学者通过较为复杂的算法,例如神经网络、模型预测等,设计了较为复杂的控制器去抵消输入饱和及不确定性扰动带来的影响;而针对抗饱和辅助系统及扰动观测器的研究较少。

基于上述问题,本文的贡献如下。

(1)针对AUV水平面模型存在不确定性扰动的情况,通过设计非线性扰动观测器估计AUV受到的不确定性扰动,从而降低不确定性扰动所带来的影响。

(2)引入指令滤波器,消除了对虚拟控制量求导时的微分爆炸现象。

(3)针对AUV所拥有的输入饱和状况,设计一个抗饱和的辅助系统,从而抵消AUV输入饱和的影响,进而提高AUV水平面轨迹跟踪的稳定性。

1 AUV水平面模型建立

1.1 AUV连续系统水平面模型

对于水下航行器运动,通常需要建立六自由度AUV的动力学和运动学模型。本文研究水下机器人在水平面上的运动空间;忽略水下机器人在竖直方向的运动,考虑AUV在水平面的三个自由度,考虑AUV在水平面上前进速度u、横漂速度v和偏航角度三个自由度,将空间6自由度运动分解为3自由度水平面运动。利用固定坐标系(定系E)和运动体坐标系(动系B)来描述AUV在水平面的运动,建立AUV水下运动学和动力学模型。AUV水平面坐标变换及轨迹跟踪示意图,如图1所示。

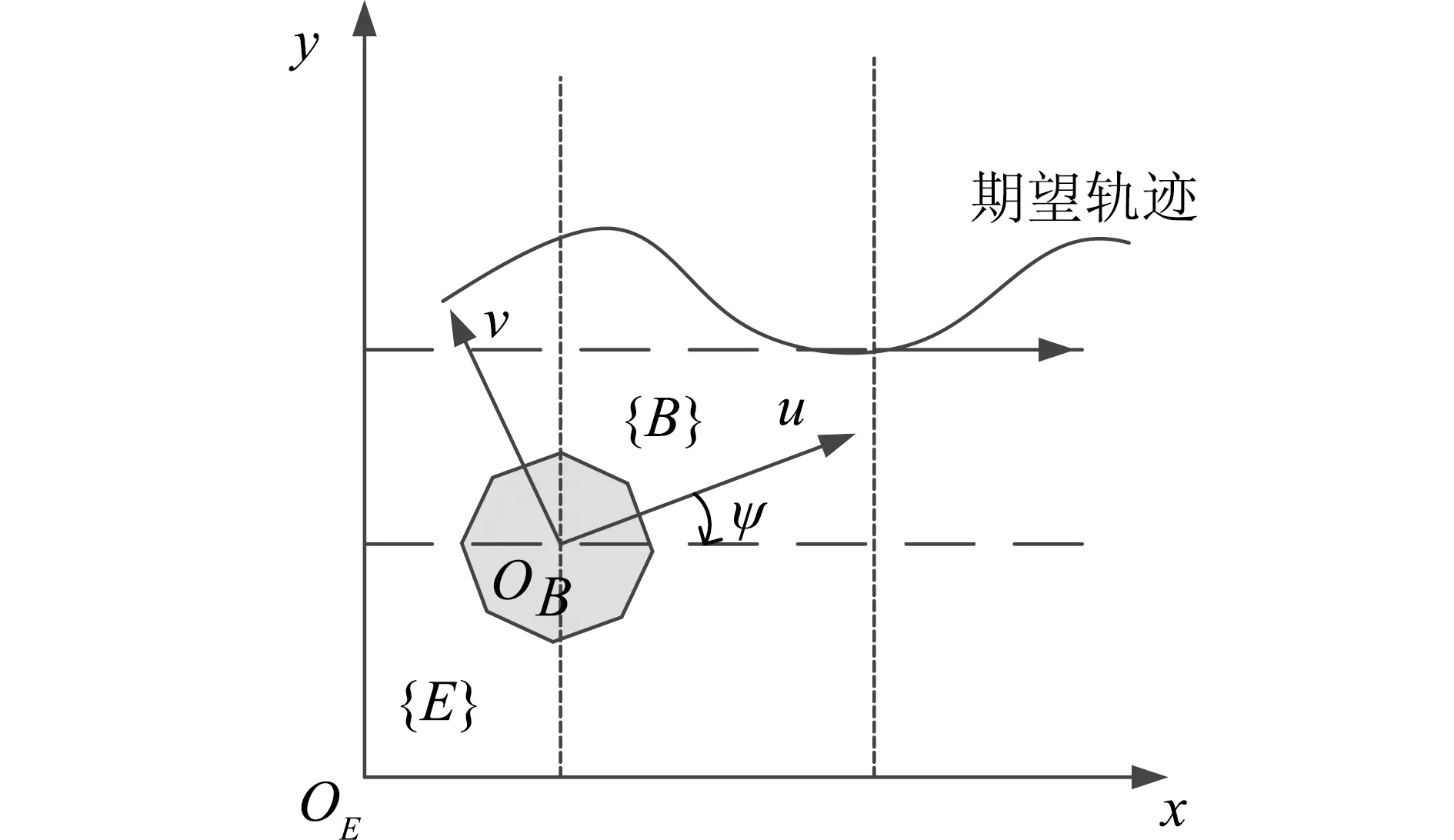
图1 AUV水平面坐标变换及轨迹跟踪示意图

AUV水平面运动学及动力学模型,如式(1)所示。

(1)

式(1)中,η=[x,y,Ψ]表示AUV在固定坐标系{E}下的位置向量,由AUV的实际位置(x,y)及其偏航角Ψ组成,Ψ是AUV的航向与ox轴方向的夹角,取逆时针方向为正;v=[u,v,r]表示在运动坐标系下的AUV速度向量,u为前进速度、v为横漂速度、r为偏航角速度;τ=[τu,τv,τr]T为AUV的控制输入,τu为前进方向控制力、τv为横漂方向控制力、τr为偏航方向控制力矩;Δ=[Δu,Δv,Δr]T∈R3为在运动坐标系下由海流引起的环境干扰,M为可逆的正定对称矩阵,表示包括附加质量的惯性矩阵;C(v)∈R3×3表示科里奥利及向心力矩阵;D(v)∈R3×3是非线性水动力阻尼矩阵;通过旋转矩阵R(Ψ)可将运动体坐标系转换为固定坐标系,且R(Ψ)R-1(Ψ)=I3,即R-1(Ψ)=RT(Ψ),R(Ψ)旋转矩阵表达形式如式(2)所示。

(2)

同时,M、C(v)∈R3×3、D(v)∈R3×3表达形式如式(3)-式(5)所示。

(3)

(4)

(5)

1.2 AUV水平面控制系统设计

本文基于Lyapunov理论和Backstepping理论,为了对AUV进行轨迹跟踪控制,在反步法中结合滑模变结构控制理论,闭环控制系统构建如图2所示。

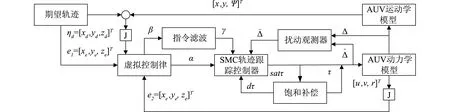
图2 轨迹跟踪控制流程图

在AUV模型存在执行器输入饱和及不确定性扰动的情况下,会使AUV轨迹跟踪的误差较大。为降低输入饱和对AUV轨迹跟踪运动的影响,设计抗饱和辅助系统对其执行器输入饱和进行补偿;设计非线性扰动观测器来估计AUV受到的不确定性扰动,以降低不确定性扰动对AUV控制的影响;为克服对虚拟控制律求导过程中会出现“微分爆炸”现象,在此引入指令滤波来克服此缺点;最后,再根据AUV水平面运动学及动力学模型,结合滑模变结构控制理论,设计AUV轨迹跟踪滑模控制器。

2 AUV水平面轨迹跟踪反步控制

2.1 扰动观测器设计

为观测水平面的不确定性扰动,基于Lyapunov理论和Backstepping理论及AUV水平面运动学及动力学模型,设τ=[τ1,τ2,τ3],定义干扰观测器设计的辅助变量为Ξ,设该辅助变量Ξ如式(6)所示。

Ξ=v-χ

(6)

式(6)中,对χ求导,有:

(7)

式(7)中,λi=R3×3(i=1,2,3)为观测器的辅助状态矩阵,为对角矩阵,且λ2>ρ;

式(6)对时间求导如式(8)所示。

(8)

将扰动观测器设计如式(9)所示。

(9)

为了证明扰动观测器的性能,定义扰动观测器的估计误差如式(10)所示。

(10)

将式(9)代入式(10)可得式(11)。

(11)

由式(11)可知,该扰动观测器的观测值可以保证收敛。

选择Lyapunov函数如式(12)所示。

(12)

对式(12)求导如式(13)所示。

=ΞT(-λ1Ξ+λ2sgn(Ξ)-Δ)

≤λ1(ΞTΞ)

≤0

(13)

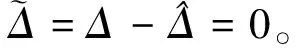
2.2 反步滑模控制器设计

本小节将基于Lyapunov理论和Backstepping理论,由AUV水平面运动学及动力学模型来设计AUV水平面轨迹跟踪滑模闭环控制器,并设计抗饱和辅助系统来补偿执行器输入饱和。

由AUV水平面运动学及动力学模型式(1)可得式(14)。

(14)

第一步,设置AUV水平面运动轨迹期望为ηd,定义AUV轨迹跟踪位置误差向量e1,建立水平面轨迹误差方程如式(15)所示。

e1=η-ηd

(15)

并将式(14)代入式(15)并对其求导,可得式(16)。

(16)

构建李雅普诺夫函数V1如式(17)所示。

(17)

对式(17)求导如式(18)所示。

(18)

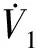
(19)

式(19)中,c1∈R3×3为正定对角矩阵。

为了得到β的导数,解决Backstepping的微分爆炸问题,我们引入指令滤波,指令滤波方程如式(20)所示。

(20)

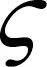
根据式(20),得到的滤波误差向量如式(21)所示。

γ=α-β

(21)

第二步,定义AUV速度跟踪误差向量e2,建立水平面速度误差方程如式(22)所示。

e2=υ-α

(22)

将式(22)代入式(18),如式(23)所示。

=e1(R(Ψ)(e2+γ)-c1e1)

(23)

为使速度跟踪误差向量e2趋于稳定,设计积分滑模面s如式(24)所示。

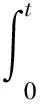
(24)

对式(24)求导可得式(25)。

(25)

为了提高AUV控制系统收敛效率以及动态响,应设计趋近律如式(26)所示。

(26)

式(26)中,k>0,ε>0为待设计参数,0<ξ<1。

结合李雅普诺夫理论和反步法,构建李雅普诺夫函数V2如式(27)所示。

(27)

对式(27)求导,如式(28)所示。

(28)

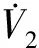
(29)

将式(29)代入式(28),如式(30)所示。

(30)

(31)

AUV运动的过程中通常存在着制动器输入饱和的问题,为了消除该影响,设计如下抗饱和系统来补偿制动器输入饱和如式(32)所示。

(32)

式(32)中,dτ=satτ-τ为输入误差,k>0,κ是一个较小的正参数;

由此在制动器存在输入饱和情况下,可将其控制律设计如式(33)所示。

(33)

2.3 稳定性分析

本小节将基于Lyapunov理论和Backstepping理论,分析滑动面及抗饱和系统的稳定性。

为证明积分面s及抗饱和系统w的稳定性,构建李雅普诺夫函数V3如式(34)所示。

(34)

对式(34)求导可得式(35)。

(35)

考虑在输入饱和的情况时,以下式子成立,如式(36)和式(37)所示。

(36)

(37)

将式(36)和式(37)代入式(35),并整理如式(38)所示。

(38)

又由不等式关系,可得式(39)。

(39)

所以,可将式(39)整理为式(40)。

(40)

(41)

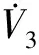
基于上述稳定性分析证明:AUV水平面的轨迹跟踪控制在控制律式(33)的作用下,能够达到控制目标,即该控制系统能够实现稳定运行。

3 AUV水平面仿真研究

3.1 模型参数

为证明控制器的有效性和鲁棒性,对设计的基于扰动观测器的AUV水平面轨迹跟踪滑模控制器进行了仿真分析,在Matlab/Simulink软件上进行运动仿真,仿真中所用到的AUV模型参数如表1所示。

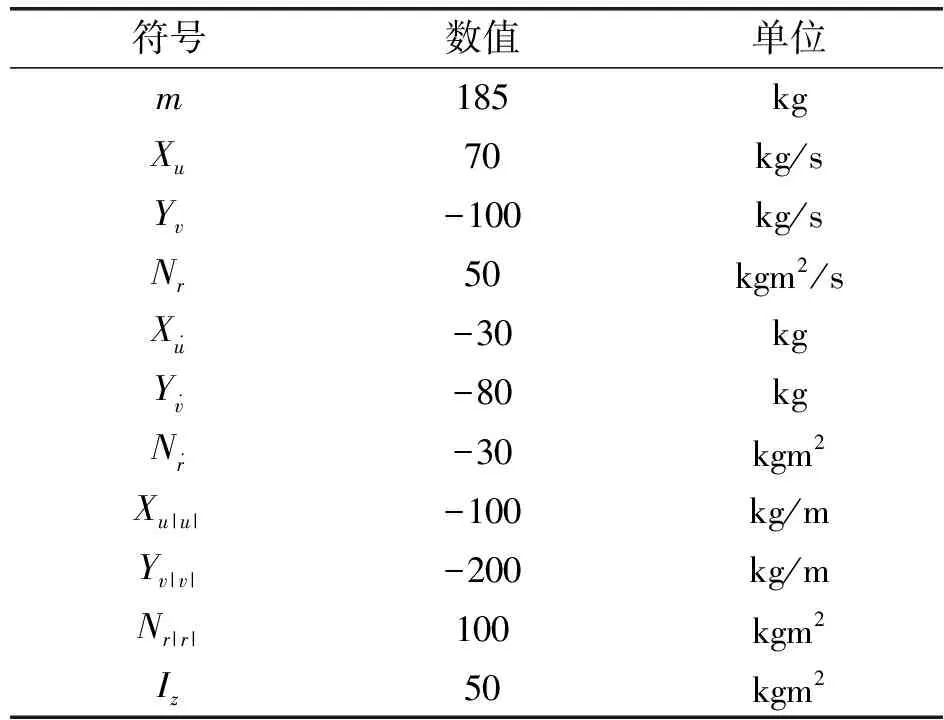
表1 AUV主要模型参数

3.2 仿真结果

为了进一步验证所设计控制器的有效性,故设计一组水平面复合轨迹进行跟踪,设其轨迹方程如式(42)所示。

(42)

在仿真环境的设定中,将外界扰动设定为连续的扰动,即:Δ1=10,Δ2=0.3。所设计的控制器参数为c1=5,c2=2,σ=0.1。滤波器参数为f=25,ζ=0.7。抗饱和辅助系统参数为k=10,κ=0.01。

如图3和图4所示,AUV可以快速跟踪目标轨迹,跟踪误差较小,最终趋于零。如图5所示,AUV可以快速到达期望速度并保持恒定速度进行跟踪。如图6所示,AUV轨迹跟踪控制输入也在控制的范围内,并且相对平缓。

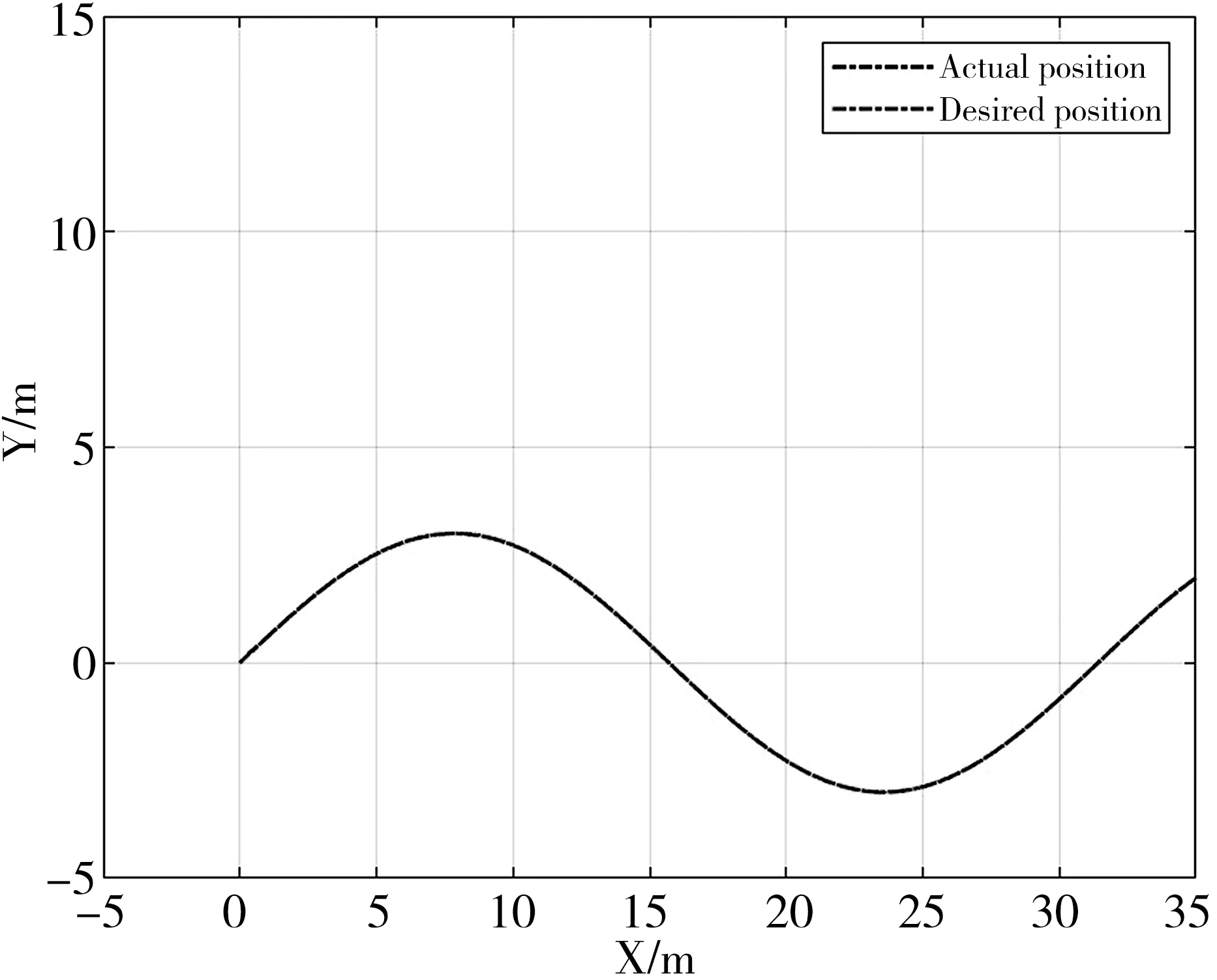
图3 AUV轨迹跟踪曲线

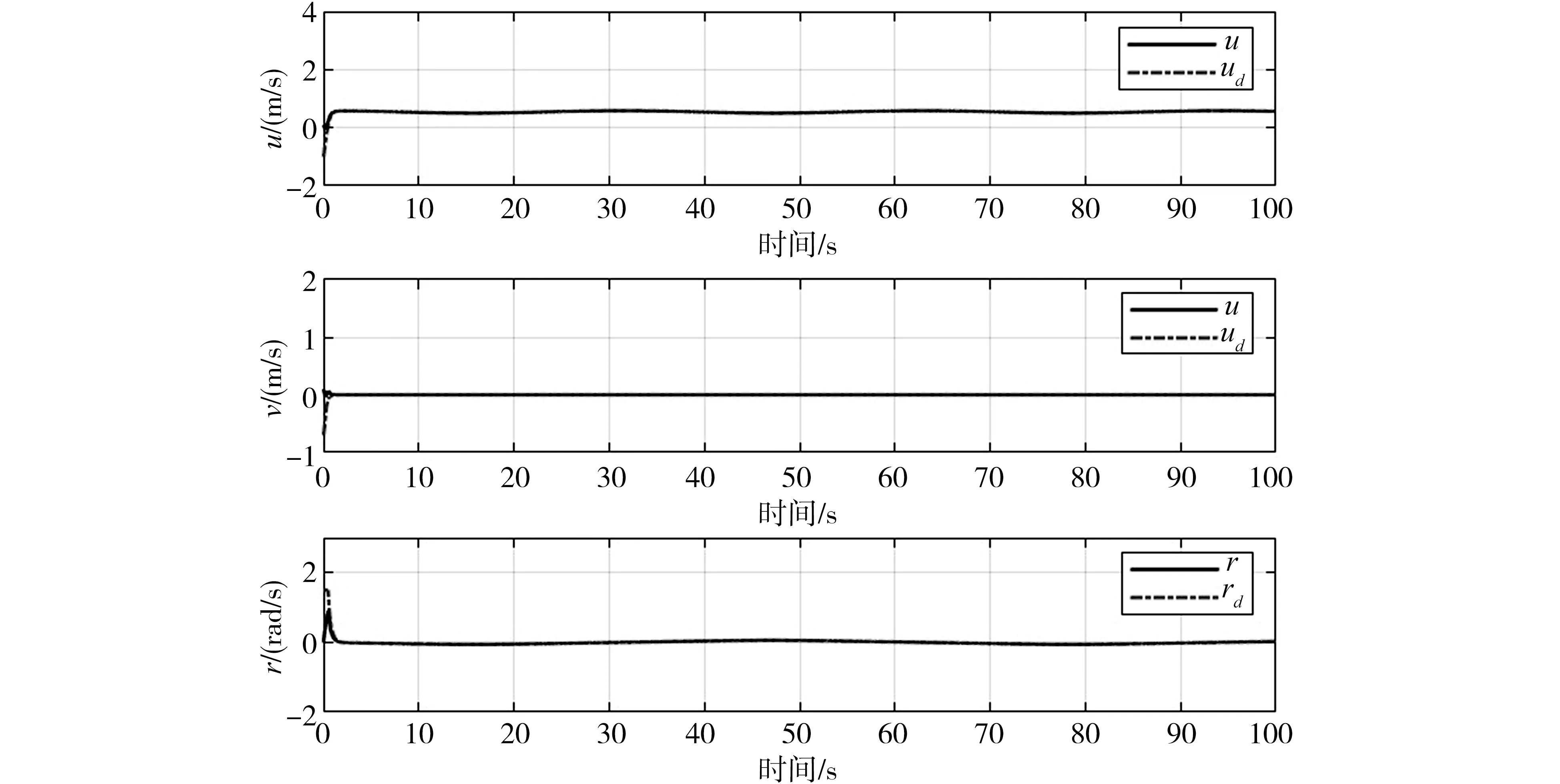
图5 AUV速度跟踪曲线

图6 AUV轨迹跟踪控制输入

4 结论

本文针对AUV在水平面的轨迹跟踪问题,设计扰动观测器观测水中的不确定性扰动;存在执行器输入饱和的情况下,设计抗饱和辅助系统抵消执行器输入饱和;通过Backstepping理论与动态滑模控制理论,设计了AUV水平面轨迹跟踪控制器;其仿真结果表明,本文所设计的控制器可以实现AUV在水平面上轨迹跟踪,并跟踪其速度误差,使AUV能够保持稳定的航速,快速跟踪上期望轨迹,且跟踪误差很小,最终趋向于0;本文设计的抗饱和辅助系统能使AUV输入稳定在一个有限的边界内,从而提高了AUV的控制精度,使AUV的轨迹跟踪达到了理想的效果。