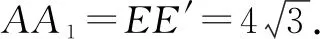高考命题特点分析,合理引导复习备考
江苏省海门中学 汪香丽
近两年的新高考数学试卷坚持“以德为先,能力为重,全面发展”的高考创新命题理念,稳妥推进新旧高考的过渡、改革与发展,走出一条深化基础、加强综合、创设情境、着力创新、注重衔接等具有一定特色的高考之路,在合理引导中学数学教学、全面落实“双减”等方面都发挥着积极有效的作用.
1 深化基础,注重教考衔接
高考命题有效深化基础性,全面落实数学基础知识的考查与应用,这也在很大程度上引导高中数学教学与学习,强调夯实数学知识基础,掌握数学基本方法,积累数学经验活动等.
近两年的新高考数学命题主要从以下三个方面着力:(1)知识考查重理解;(2)技能考查重熟练;(3)方法考查重积累.合理有效地实现深化基础这一基本考查目标.
例1(2022年高考数学新高考Ⅱ卷·13)已知随机变量X服从正态分布N(2,σ2),且P(2
分析:利用随机变量X服从正态分布,结合正态分布曲线的对称性,通过数据的分析与计算来求解.
解析:由随机变量X服从正态分布N(2,σ2),可得P(2
所以P(X>2.5)=0.5-0.36=0.14.
点评:通过数据分析与处理,结合正态分布曲线的对称性来解决正态分布中的基础问题.正确的数据分析与处理,是利用基础知识与基本技能解决数学问题最重要的一个环节,也为一些综合应用问题的深入与拓展打下基础.
2 加强综合,发挥选拔功能
高考命题合理加强综合性,这样就能形成同一知识内容的交汇,不同知识内容的融合,在不同模块、不同章节的数学基础知识之间形成综合性,可以更加有效、全面地考查学生分析问题与解决问题的能力等,能更好地体现选拔与区分功能.
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
分析:根据等差数列的定义与基本性质,并结合充分必要条件的定义与判断方式,从充分性与必要性两个方面加以分类讨论判断即可.

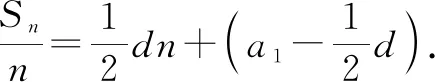

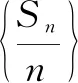
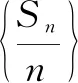

由Sn-Sn-1=an,得an=nan+1-(n-1)an-2nt,整理有an+1-an=2t为常数.
当n=1时,an+1-an=2t也成立.
故{an}为等差数列,则甲是乙的必要条件.
综上分析,可知甲是乙的充要条件.
故选择答案:C.
点评:该题以一道简单的充分必要条件的判断来创设情境,巧妙融入等差数列的概念与基本性质、数列的函数性、充分必要条件的概念等,实现基础知识之间的综合与应用.
3 创设情境,强调学以致用
近两年的新高考数学试题的情境创设各式各样,有以纯数学情境出现的概念、原理、运算等问题,有以探究、数据分析、科学实验等创新情境出现的应用问题,等等.
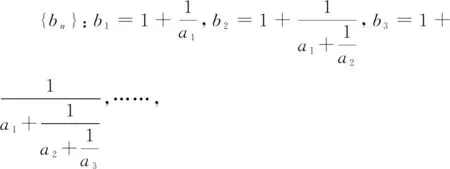
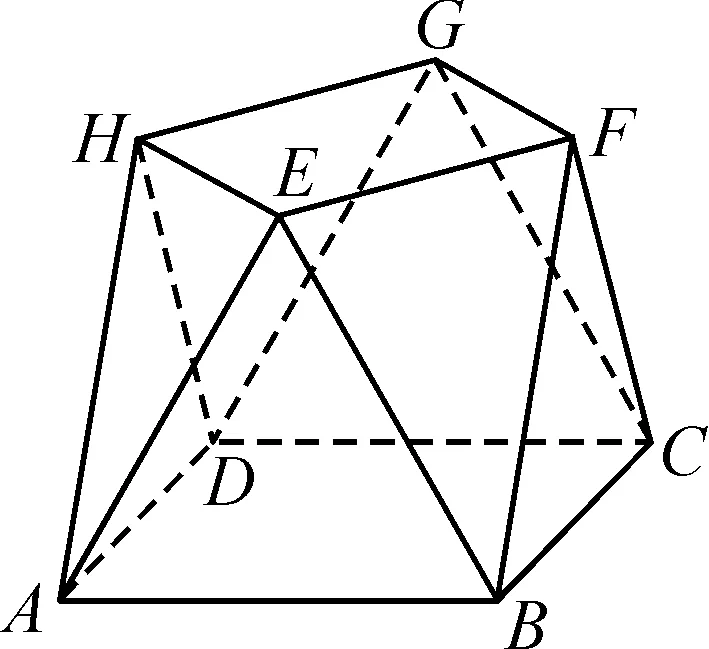
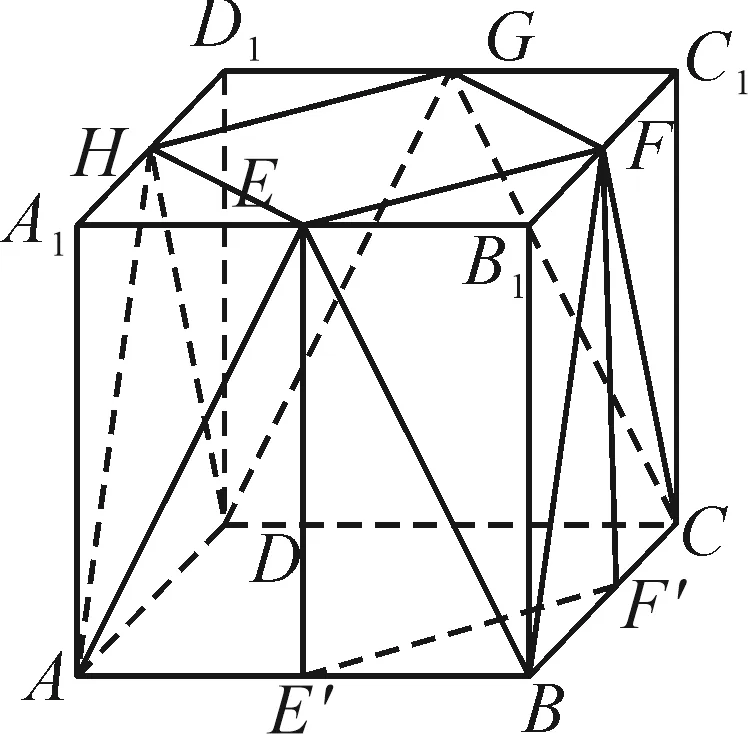
A.b1 分析:根据题设条件,利用数列递推关系式的结构特征以及不等式的性质,依次推导数列前若干项与后面各项之间的大小关系,结合具体选项即可正确分析与处理. 所以只有选项D正确,同样可以借助以上不等式的性质加以判断.故选择答案:D. 高考命题全面着力创新性,这也是2022年高考数学试卷的一大特色,吻合当今时代潮流与对人才选拔的基本要求.借助问题的创新性设置与创新性应用,可以在更大的范围内了解与考查学生的创新意识与创新应用能力,进而合理区分不同层次学生的水平与差异,为高校选拔相应的人才,特别是创新性、应用性方面的人才. 例4(2022年高考数学全国甲卷文科·19)小明同学参加综合实践活动,设计了一个封闭的包装盒.包装盒如图1所示:底面ABCD是边长为8(单位:cm)的正方形,△EAB,△FBC,△GCD,△HDA均为正三角形,且它们所在的平面都与平面ABCD垂直. 图1 (1)证明:EF∥平面ABCD; (2)求该包装盒的容积(不计包装盒材料的厚度). 分析:(1)将几何体补形之后结合直线与平面平行的判断定理即可证得结论;(2)关键是确定几何体的空间特征,然后结合相关的棱长即可计算其体积. 解析:(1)如图2所示,将几何体补形为长方体,作EE′⊥AB于点E′,FF′⊥BC于点F′.因为底面ABCD为正方形,△ABE,△BCF均为等边三角形,所以EE′=FF′. 图2 由两个平面垂直的性质可知,EE′,FF′均与底面ABCD垂直,则EE′∥FF′.所以四边形EE′F′F为平行四边形,则EF∥E′F′. 点评:本题以包装盒设计为背景,以学生很少见到的几何体为研究对象合理创设,新颖别致.解答本题的关键在于正确作出辅助线,将不熟悉的几何体转化成若干个熟悉的几何体.有效考查了直线与平面平行的判定、直线与平面垂直的判定、两个平面垂直的性质、长方体与棱锥的体积公式等知识,以及空间想象、逻辑思维和数学运算等方面的能力. 近两年的高考数学,其基础性有所巩固,创新性有所增强,难度有所提升,充分反映了国家对拔尖人才选拔的需求.这也要求我们在高三数学复习教学与备考过程中,回归教材,巩固基础,因材施教,分层教学,精准把握,提升能力.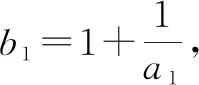
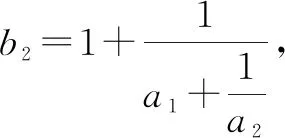
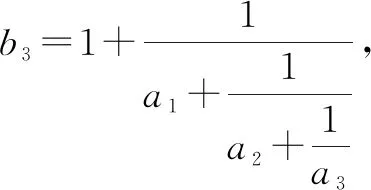
4 着力创新,考查学习潜能