文化情境创设,数列知识应用*

江苏省口岸中学 陈春花

数列作为高中数学的一大主干知识,其与数学文化情境的渗透与融合,有着丰富的应用场景,现选取四个方面的案例与大家分享.

1 数学名著

例1[2022—2023学年辽宁省沈阳四中高三(上)月考数学试题(9月份)]南宋数学家在《详解九章算法》和《算法通变本末》中提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,高阶等差数中前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列.现有高阶等差数列,其前7项分别为1,2,5,10,17,26,37,则该数列的第19项为( ).

A.290 B.325 C.362 D.399

分析：本题选择数学名著中的垛积公式作为文化背景.先由条件判断该高阶等差数列为逐项差数之差成等差数列,得到an+1-an=2n-1,再利用累加法求得数列的通项公式,进而可求得对应项的值.

解析：设该数列为{an},则由a2-a1=2-1=1,a3-a2=5-2=3,a4-a3=10-5=5,a5-a4=17-10=7,……,可知该数列逐项差数之差成等差数列{bn},其首项为1,公差为2,所以bn=1+2(n-1)=2n-1,故an+1-an=bn=2n-1.

于是a2-a1=1,a3-a2=3,a4-a3=5,……,an-an-1=2n-3.

所以an=(n-1)2+a1=(n-1)2+1,则a19=182+1=325.故选择答案:B.

2 历史律法

例2[2022年华大新高考联盟高考数学教学质量测评试卷(3月份)]十二平均律是我国明代音乐理论家和数学家朱载堉发明的.明万历十二年(公元1584年),他写成《律学新说》,提出了十二平均律的理论.十二平均律的数学意义是:在1和2之间插入11个数,使包含1和2的这13个数依次成递增的等比数列,记插入的11个数之和为M,插入11个数后这13个数之和为N,则依此规则,下列说法错误的是( ).

C.M>3

D.N<7

分析：本题选择“十二平均律”作为文化背景,考查了等比数列的通项公式、前n项和公式、比较大小等基本知识.

解析：设递增的等比数列为{an},公比为q.

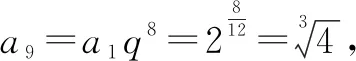
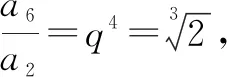
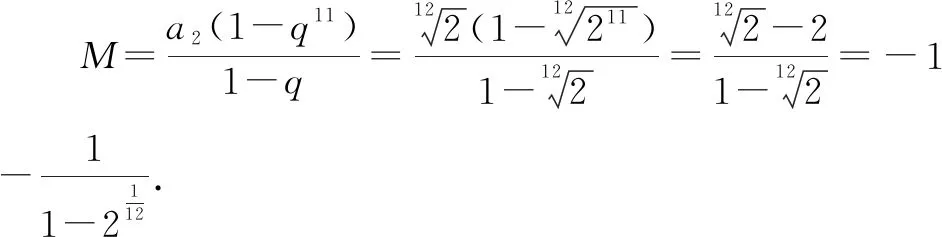
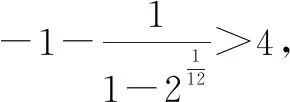
故选择答案:D.

点评：借助历史律法中数学文化情境下的数列问题,通过一些历法、音乐、美术等方面的历史文化遗产来创新设置,融入数列的基本概念等基础知识,结合实际问题以及学科交叉融合进行综合与创新应用.

3 古代建筑

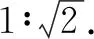
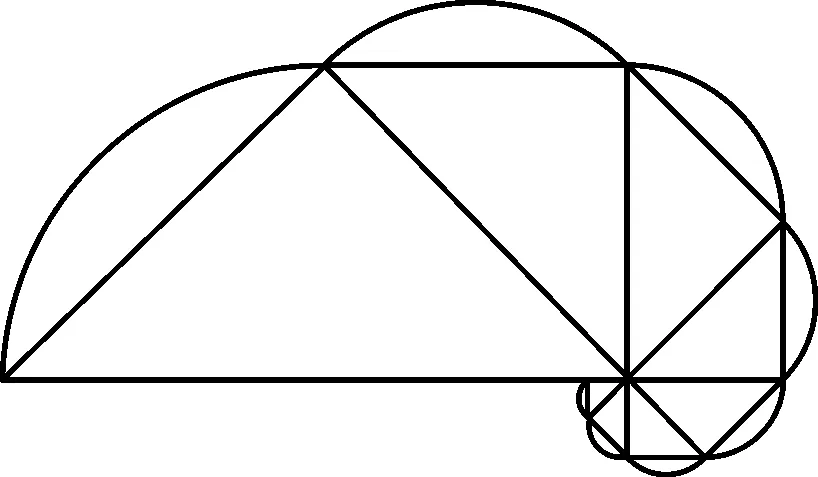
图1

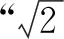
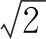
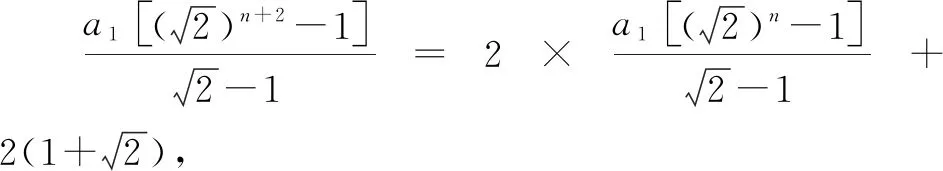
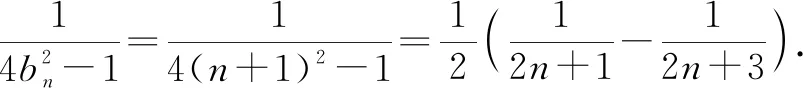
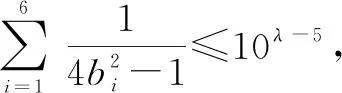
故填答案:5.

点评：巧妙融入建筑、美术、数学等多个相关学科的知识,交汇综合,抓住特色建筑的数学模型合理构建相应的数列模型,利用相关数列的基础知识与基本思想方法来解决问题.

4 经典模型

例4[2022年重庆市巴蜀中学高三(上)适应性数学试卷(四)](多选题)在1261年,我国南宋数学家杨辉所著的《详解九章算法》中提出了如图2所示的三角形数表,这就是著名的“杨辉三角”,它是二项式系数在三角形中的一种几何排列.从第1行开始,第n行从左至右的数字之和记为an,如,a1=1+1=2,a2=1+2+1=4,……,{an}的前n项和记为Sn,依次去掉每一行中所有的1构成的新数列2,3,3,4,6,4,5,10,10,5,……,记为bn,{bn}的前n项和记为Tn,则下列说法正确的是( ).

图2

A.S10=1 022

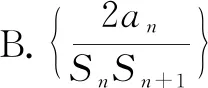
C.b57=66

D.T57=4 150

分析：本题选择“杨辉三角”这个经典模型作为文化模型,构造出两个新数列.

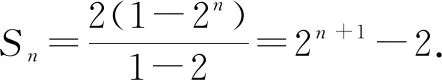
于是S10=211-2≠1 022,故选项A错误.

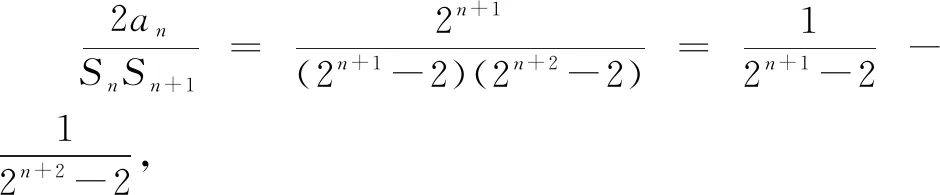
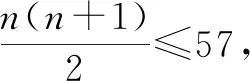
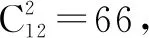
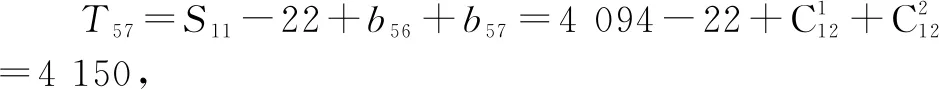
故选择答案:BCD.

点评：结合“杨辉三角”这一经典的数字模型的排列规律,融合数列、二项式定理、排列组合等相关知识,巧妙逻辑推理,合理数学运算,进而得以分析与处理创新文化情境问题.

数学不仅仅是“科学的数学”,而且还是“文化的数学”.而数学文化创新情境下的数列综合应用问题,只是其中的一个典型代表,是国家文化素质教育的重要组成部分,是在实践过程中不断探索形成的数学史、数学精神及其应用等.借助数学文化创新情境的设置,将数学知识、思想方法、数学文化等融为一体,全面检测学生的数学基础知识、思维广度与深度,不断挖掘学生潜能.