大学生数学认知结构发展特点的探析
马艳园
摘 要:数学认知结构是内化了的数学知识结构,“数学理解”是学习者获取数学知识的基本途径,对数学认知结构的发展有着积极的推进作用。从学习者数学理解的心理过程来看,“实变函数”的课程内容高度抽象,理解难度较大,在这个过程中,大学生数学认知结构的发展特点为:个体差异性、机械记忆下的积累、数学认知结构的各个子系统发展步调不一致。在新旧认知结构相互作用下,按照螺旋式的方式不断发展。
关键词:数学认知结构;数学理解;精致;个体差异性;螺旋式的发展
中图分类号:G642 文献标识码:A 文章编号:1673-7164(2023)14-0143-04
“实变函数”的课程内容抽象程度较高,理解难度较大,本校数学专业学生在学习过程中存在诸多问题,譬如数学概念的学习偏重工具性理解,对概念本质属性的认识比较浅显;不重视隐性知识的学习;知识与知识之间的联系比较薄弱等,比如,对黎曼积分与勒贝格积分之间的区别理解不到位。这些问题从不同层面影响了学生数学认知结构的构建。
一、大学生数学认知结构的发展过程
我国著名数学教育学家曹才翰、蔡金法在所著的《数学教育学概论》(1989)中首次明确提出了数学认知结构的概念[1],并对数学认知结构的内涵、特点进行了分析。他们认为,数学认知结构是学生头脑里的数学知识按照自己的理解深度、广度,结合自己的感觉、知觉、记忆、思维、联想等认知特点,组合成的一个具有内部规律的整体结构[1]。
在对“数学理解”的研究中,赫伯特和卡朋特(Hiebert & Carpenter)认为,“一个数学的概念或方法或事实被理解了,如果它成为个人内部网络的一个部分。”[2]李士锜认为,“学习一个数学概念、原理、法则,如果在心理上能组织起适当的有效的认知结构,并使之成为个人内部的知识网络的一部分,那么才说明是理解了。”[2]
不管是对数学认知结构的研究还是对“数学理解”的研究都表明,学生数学认知结构的发展依赖于对数学知识的理解,即学生通过理解数学知识构建自身头脑中知识网络——数学认知结构。因此,“数学理解”能够有效促进数学认知结构的形成,是数学认知结构发展的基本途径。
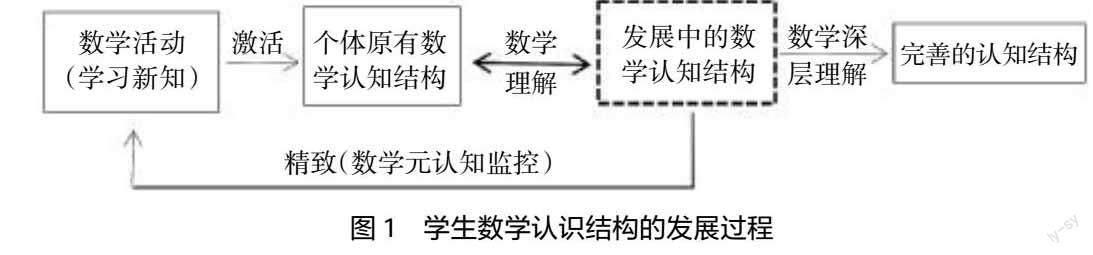
学生数学认知结构的发展过程如图1所示:
学习者对新知识的学习是一个循序渐进,由浅入深的理解过程。通常在初学阶段,对新知识的理解往往一知半解,甚至对新知识有错误认知。这些情况下形成并发展起来的数学认知结构是不完善的,学习者需要对数学认知结构进行精致。精致是对原有认知结构的重组,或者是对原有认知结构缺陷进行补修[3]。对数学认知结构的精致,会出现多次循环,直到学生对数学知识有了深层次的理解,数学认知结构在理解逐渐深刻的进程中变得更加完善。
在对数学认知结构的精致过程中,学习者必须对自身的认知过程进行积极的监控,明确理解上的不足,才能做出有针对性地查缺补漏,及时调整认知策略,对数学认知结构进行有效的精致,从而获得对新知的正确理解。
下面文章将从“數学理解”的角度,在“实变函数”的学习过程中,对本校大学生数学认知结构发展过程中呈现出的一些特点作深入研究。
二、大学生数学认知结构的发展特点
在“数学分析”的基础上,“实变函数”对知识进行了衍生和拓广。无论是数学符号还是数学思想方法,抽象程度更高。例如线段的长度,平面几何图形的面积和立体图形的体积,其本质都是对“点集”的度量,对一般点集的度量即为“实变函数”中的“测度”。对“度量对象”的推广,学生的认知需要打破常规的“几何实体”的限制。在方法上,“实变函数”处理问题的一种重要方法是分析语言与集合语言之间的转换,学生需要明确不同语言在描述同一数学知识时的异同。“实变函数”中的另一个重要思想是利用简单函数列逼近可测函数,学生需要从函数列的点点收敛来理解简单函数列收敛于可测函数的内涵。
“实变函数”中的学习对象以及课程中的数学思维方式都变得更为抽象,对学生的数学理解能力的要求也越来越高。在这种高要求下,学生需理解数学知识的过程中数学认知结构的发展变化具有什么特点?
(一)数学理解的个体差异性
不同学生在面对同一个数学情境时,会有不同信息理解、分析、处理方式[4]。因此,学生通常是按照自己对知识的理解深度,结合自己的认知方式去构建知识体系,这就使得学生头脑中数学认知结构的发展带有明显的个体差异性。
例如勒贝格(Lebesgue)可测集的学习。
定义1[5]:设E?奂Rn,若对于任意点集T?奂Rn,都有
m*(T)=m*(T∩E)+m*(T∩Ec)
则称E为L可测集,这时E的L外测度m*E即称为E的L测度,记为mE,其中T为实验集。
学习过程中,部分学生能够利用定义1证明一个点集是勒贝格可测集,但却不清楚定义1中的实验集T的意义是什么?学生的证明更多的是一种机械性模仿。这部分学生的头脑中,对可测集的理解偏重于工具性理解。工具性理解表现为理解事实性知识是什么,未完全认识,乃是一种机械记忆[6]。他们对可测集的知觉更多是在符号上的形式推导。另一部分学生会去思考实验集T的意义,这部分学生更加注重概念本质属性的学习,在教师的引导下,学生能够从内侧度与外侧度相等的条件下理解T的含义;能够明确在卡式条件下,用外侧度定义的勒贝格测度能够满足测度公理,因此,他们对勒贝格可测集的认知不仅仅是停留在符号的形式推理层面。学生对数学概念的不同认知,体现了个体头脑中构建的数学认知结构具有差异性。
(二)数学认知结构中的各个子系统发展步调不一致
数学知识分为:陈述性知识、程序性知识、过程性知识[7]。喻平教授的研究表明,在数学学习过程中,通过对陈述性知识、程序性知识、过程性知识的理解,学生头脑中分别获得了关于陈述性知识的图式、构建了产生式系统、形成了关系表征和观念表征。这三种知识的学习结果构成了数学认知结构的三个子系统,其中陈述性知识图式的构建是学习的基础,三个子系统相互作用、相互影响。
在学习中把陈述性知识转化为程序性知识往往需要经过大量的练习,而过程性知识则隐性地融会贯通于整个学习过程中,要求学生不断体验、反思才能构建起深刻的关系表征和观念表征。因此,陈述性知识图式的构建相对更快而程序性知识的产生式系统和过程性知识的体验性知识系统的发展则相对滞后。
“实变函数”的学习中,相对于陈述性知识的图式,程序性知识的产生式系统和过程性知识的关系表征和观念表征系统的发展缓慢更为突出。经过一个学期的学习,学生对“实变函数”中的一些基本概念以及相关性质有基本的理解,但是在做题过程中,仍然感觉到很多“实变函数”中的题目难,甚至对此束手无策。
(三)机械记忆学习下的累积
在“实变函数”学习中,学习材料难度系数的逐渐增加,教师通常采用“结果型”的教学方式,直接把定理或性质的结论介绍给学生,再进行证明,把问题的条件、结论以及推导过程都讲述清楚,同时引导学生与原有认知结构中相关知识建立非人为的实质性联系,明确新旧知识之间的异同。但在实际学习过程中,学生的理解力往往达不到教材的难度系数要求的程度。当学生对抽象知识的理解遇到障碍时,容易出现机械性的记忆学习,对相关知识点的学习更多情况下是停留在对结果的记忆这一层面上,即学习的表面化。对知识的本质属性或者是数学符号的意义、知识之间的异同等没有更深入地探索,对知识的构建是一种机械记忆下的积累。前面勒贝格可测集的学习过程中,在学生不理解实验集T含义的情况下,利用定义证明一个集合是否是可测集,就是一种机械性的模仿。
例如可测函数的学习。
定义2[5]:设f(x)是定义在可测集E?奂Rn上的广义实质函数,若对于任意的有限实数t,点集{x∈E ∶ f(x)> t} 是可测集,则称f(x)是E上的可测函数,或称在E上可测。
调查中发现,部分学生能够用定义2证明函数f(x)是E上的可测函数,但是不清楚定义2中的任意有限实数t的意义是什么?与勒贝格可测集的学习相同,学生的证明更多的是一种机械性模仿。
例如,法图(P.Fatou)引理的学习。
定理2[5]:(P.Fatou引理)若{fn(x)} 是在上的非负可测函数列,则
在调查中,大部分学生能够正确叙述法图引理。但是没有足够的反思:法图引理中的结论为什么只考虑函数列的下极限?学生对法图引理的应用也是一种机械性迁移。
通过强行记忆而积累发展起来的数学认知结构中,学生对每个知识点的理解一知半解,知识之间缺乏有机联系,此时的数学认知结构这栋“知识大楼”是被一堆堆“砖头”杂乱无章地堆积起来的。
(四)原有认知结构和新认知结构的相互作用
认知心理学研究表明,在新知学习过程中,学习者通常会在原有数学认知结构中寻找新知识生长的固着点,以此帮助理解新知识。在这种认知心理活动中,若学生能够正确找到固着点,并且正确把握新知识与固着点之间的异同,那么固着点对新知识的学习有积极促进作用,反之则会对新知识的理解产生障碍。比如,新知識与某些旧知识之间建立起主观的而非客观事实的联系;原有的数学思维对新知识理解的局限等。
例如黎曼积分的对象是区间上“基本连续”的函数,勒贝格积分的对象是可测集上的可测函数。黎曼积分的主要思想是分割定义域,而勒贝格积分的主要思路是对函数值域进行划分[5]。事实上,分割函数值域后所得到的点集不一定是一个区间,函数的定义域也不一定是互不相交的有限个区间,而可能是一个分散且杂乱无章的点集以及并集[5]。在此,黎曼积分中“连续的”概念被打破。从黎曼积分的思维方式过渡到勒贝格积分的思维方式,黎曼积分中“连续”的思想往往会对学生理解勒贝格积分的思想产生障碍。需要学生打破原有的思维格局,对新思想、新方法认真揣摩,才有利于勒贝格积分的学习,从而促使新数学认知结构获得更好的发展。
(五)螺旋式的动态发展
斯宾塞等人的APOS理论证实了学习者对数学概念的理解是在一个循环的过程中不断深化。他们的理论里阐述了在数学概念学习中存在一个APOS循环,他们研究假设数学知识是个体在解决所感知到的数学问题过程中获得的,在这个过程中,个体依序建构了心理活动(actions)、程序(processes)、和对象(objects),最终组织成用以理解问题情境的图式结构(schemas)[2]。在“活动”阶段个体对数学概念有初步的了解,并得到初步的“程序”,当个体遇到更为复杂的概念的外延时,又会回到“活动”阶段,开展进一步的学习,完善数学概念的“程序”,经过多个循环后,个体才会形成完整的数学概念即“对象”[2]。
“实变函数”课程中的数学知识体系具有严密的逻辑性,教材按照知识之间严格的逻辑次序进行编排。学生把这套具有严格逻辑性的数学知识结构内化入自身认知结构的过程中,由于学习材料符号化、抽象化,加之学生认知能力的限制、机械记忆的学习等,使得学生对数学知识的理解并非一蹴而就,而是在一个不断“重复”理解的过程中,由浅入深,逐步提高对数学知识的认知。
数学理解的循环动态特性,反映出数学认知结构具有螺旋式动态发展的特点,即个体对数学知识进行循环理解,认知由低层次向高层次发展,随着认知活动的逐步深入和个体理解水平的不断提升,机械记忆的知识点能够重新获得理解,学生变得豁然开朗,知识融会贯通,个体的数学认知结构被不断精致,逐步达到更为精确和完善的程度。
“实变函数”里的许多概念、性质、定理等都需要反复理解,从而促进数学认知结构的不断精致。例如,学生要反复研读教材上关于可测集建立的历史过程,不断反思,才能够渐渐体会到勒贝格可测集定义中实验集T的含义。学生需要在叶果洛夫定理、里斯(Riesz)定理等相关定理和性质的证明过程中,反复理解“分析语言”和“集合语言”之间相互转换的意义。学生需要对《数学分析》和“实变函数”中的相关知识点不断地进行对比学习,才能真正掌握知识的本质属性、知识之间的异同,实现知识的“稳定性”和“可辨别性”,从而形成良好的数学认知结构。
三、结语
“实变函数”尽管课程内容较为抽象,但是作为数学专业的一门基础课,不仅对学生数学思维能力的提升有重要意义,而且是学生后续专业学习的基础。因此,在“实变函数”的学习过程中,良好数学认知结构的形成,有利于提高学生数学抽象的能力、开阔学生的数学视野、提升学生的数学素养。教师对学生数学认知结构的发展特点有科学的认识,就能够帮助教师实施有效的教学方法于“实变函数”教学中,启发学生积极思考,对数学知识有深刻的理解,从而构建良好的数学认知结构。在目前已有的研究中,课题式教学法[8],“三教—教思考、教体验、教表达”[9]的教学方法,以问题驱动为中心的教学方法[10]等,对学生在认知结构构建过程中的知识理解、思维发散、问题解决等方面都有着积极的促进作用。
参考文献:
[1] 喻平,連四清,武锡环. 中国数学教育心理研究30年[M]. 北京:科学出版社,2011:202+204.
[2] 鲍建生,周超. 数学学习的心理基础与过程[M]. 上海:上海教育出版社,2009:116+129.
[3] 喻平. 数学教育心理学[M]. 南宁:广西教育出版社,2004:151-152+162.
[4] 尚亚明,熊斌. 数学问题提出的过程性研究评述[J]. 数学教育学报,2021,30(05):66-71.
[5] 程其襄,张奠宙,魏国强,等. 实变函数与泛函分析(第四版)[M]. 北京:高等教育出版社,2019:43+54.
[6] 李春雷,于凤来. 数学理解水平的划分[J]. 数学教育学报,2022,31(04):68-73.
[7] 曹才翰,章建跃. 数学教育心理学(第三版)[M]. 北京:北京师范大学出版社,2017:95.
[8] 曹广福. 实变函数课题式教学研究[J]. 数学教育学报,2021,30(02):32-37.
[9] 唐海军,严虹,任旭. 数学合作问题解决视野下的“三教”探析[J]. 数学教育学报,2021,30(05):72-79.
[10] 沈威. 问题驱动与思想挖掘:“可积条件”教学示范课的个案研究[J]. 数学教育学报,2021,30(02):38-41.
(荐稿人:余丽,宜春学院副教授)
(责任编辑:淳洁)

