数学文化试题赏析

张圣茹 龚卫东(正高级教师 特级教师)

(1.北京师范大学乐育书院 2.深圳市高级中学)

《普通高中数学课程标准(2017 年版2020 年修订)》中强调要将数学文化融入日常教学中,它明确指出,数学文化不仅包括数学的思想、精神、语言、方法、观点,以及它们的形成与发展,还包括数学在人类生活、科学技术、社会发展中的贡献与意义,以及与数学相关的人文活动.在命题上,以数学文化为背景不仅能拓宽学生的眼界,使学生了解数学与生活的密切联系,也能综合考查与提高学生的阅读理解能力、核心素养.因此,以此为背景的高考题目也越来越多,本文以几道数学文化试题为例,谈谈相关解题策略.

1 立体几何

例1(2020年全国Ⅰ卷理3)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥(如图1).以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底边正方形的边长的比值为( ).

图1

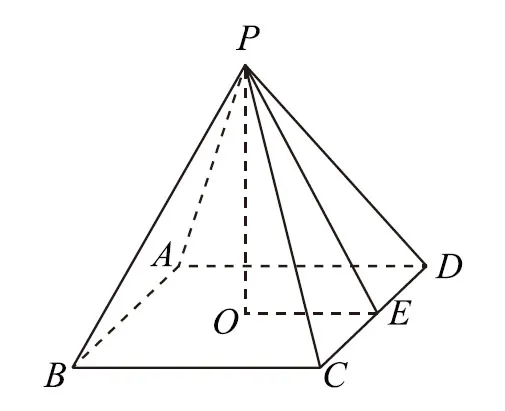
图2

点评

本题将立体几何与代数通过人类智慧结晶——金字塔进行巧妙地结合,考查学生根据题目要求设未知量以及求解运算能力,涉及逻辑推理、数学建模、数学运算以及直观想象核心素养.

2 平面几何

例2(2021年全国乙卷理9)魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作,其中第一题是测量海岛的高.如图3所示,点E,H,G在水平线AC上,DE和FG是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,EG称为“表距”,GC和EH都称为“表目距”,GC与EH的差称为“表目距的差”,则海岛的高AB＝( ).

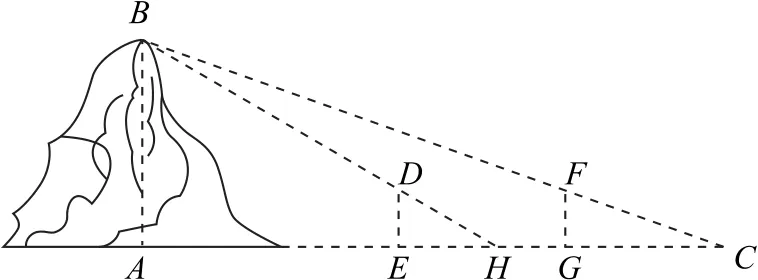
图3

解析

本题将空间中的测量问题转化为平面几何中的长度关系问题.

将图3 抽象成图4,连接FD交AB于M,则AB＝MB＋AM.

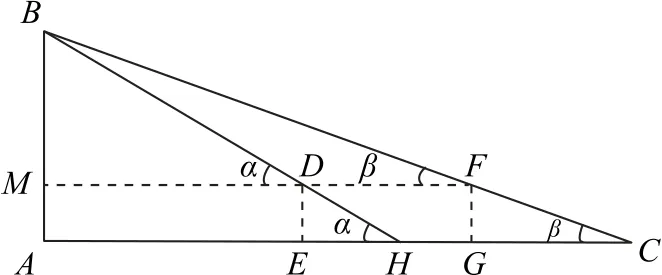
图4

点评

《海岛算经》为数学著作《九章算术注》中的一卷,《九章算术注》共十卷,全都为数学知识在实地测量中的应用.此题以此为背景,考查三角形相似、三角函数以及平面中三角形各边表示及其关系.涉及新课标中数学抽象、逻辑推理、数学建模、数学运算与直观想象核心素养.

3 等差数列

例3(2020年全国Ⅱ卷理4)如图5所示,北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层,上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块,下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块,已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)( ).

图5

A.3699块 B.3474块

C.3402块 D.3339块

解析

根据题意,可知天坛三层由内到外每环的扇面形石板块数构成首项为9、公差为9的等差数列,设第n环的扇面形石板数目为an,Sn为{an}的前n项和,设每层都有n环,则

解得n＝9,从而S3n＝S27＝3402,故选C.

点评

本题以贴近生活的情境为背景,考查学生对等差数列的通项公式等基本知识的掌握情况,反映了我国古代的建筑成就,有利于激发学生对中华优秀传统文化的热爱之情,使学生领悟到数学之美.

4 等差与等比数列结合

例4(2021年全国Ⅰ卷16)某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴把纸对折.规格为20dm×12dm 的长方形纸,对折1次共可以得到10dm×12dm,20dm×6dm 两种规格的图形,它们的面积之和S1＝240dm2,对折2次共可以得到5dm×12dm,10dm×6dm,20dm×3dm三种规格的图形,它们的面积之和S2＝180dm2,以此类推,则对折4次共可以得到不同规格图形的种数为__________;如果对折n 次,那么

解析

本题以剪纸中的图形面积变换为背景,通过构建数列求解.根据题意,对折4次可以得到五种规格的图形,通过数学归纳法,可知对折n次可得到(n＋1)种不同规格的图形,每种规格图形的面积均为dm2,它们的面积之和为因此

点评

中国剪纸作为非物质文化遗产,是中国文化的重要组成部分,剪纸过程中利用到的技法是数学知识的具象化.本题考查数列求和的知识点,使学生更深入了解中华优秀传统文化,体会数学在生活中的应用.

5 变式巩固

练习1如图6所示,唐金筐宝钿团花纹金杯出土于西安,这件金杯整体造型具有玲珑剔透之美,充分体现唐代金银器制作的高超技艺,是唐代金银细工的典范之作.该杯主体部分的轴截面可以近似看作双曲线C的一部分,若C的中心在原点,焦点在x轴上,离心率e＝2,且点在C上,则双曲线C的标准方程为( ).

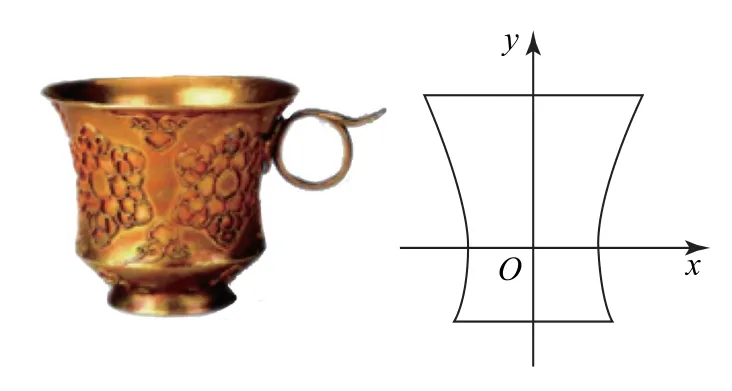
图6

答案B.

练习2《算法统宗》是中国古代数学名著,由明代数学家程大位编著,它对中国民间普及珠算和数学知识起到了很大的作用.在这部著作中,许多数学问题都是以歌诀形式呈现的,如“九儿问甲歌”就是其中一首:一个公公九个儿,若问生年总不知,自长排来差三岁,共年二百又零七,借问长儿多少岁,各儿岁数要详推.在这个问题中,记这位公公的第n个儿子的年龄为an,则a3＝( ).

A.14 B.18 C.29 D.32

答案C.

6 小结

每道题目考查的知识点并不单一,凸显出数学核心素养考查的多元化.以数学文化为命题背景的试题难度多为中下,多出现于选择题或填空题,涉及数学史、数学与科技、数学与人文、数学与艺术、数学与生活等多个方面,具有经典性、时代性、创新性等特点.

就几何和数列而言,中国古代的《张丘建算经》中涉及的等差数列各元素互求,《九章算术注》中出现的众多测量计算以及图形变换,西方欧几里得的《几何原本》中展现出欧氏平面诸多定理的强大,都对学生了解数学思想史,感悟数学的发现过程与现实应用有一定帮助.

无论数学文化题目的背景如何改变,高考数学对学生数学知识与能力以及数学核心素养的考查总目标不变,在实际教学中,教师应注意“情境设定”,让学生经历完整的知识构建以及建模过程,领悟数学的本质,促进学生学科核心素养的发展,将知识与文化、科技等融合,发挥育人作用.

(完)