整体法和隔离法在高中物理解题中的应用思路

王 辉

(安徽省利辛县第一中学,安徽 利辛 236700)

掌握有效的解题方法可以帮助学生攻克学习的难关,但是我们发现在高中物理课的学习中,许多学生并没有掌握有效的问题解决方法,从而导致解题速度慢、正确率低等,影响了考试的成绩,因此,需要高中物理教师指导学生走出机械的解题误区,能够掌握有效的解题技巧与方法,其中整体法与隔离法的掌握是十分必要的,可以为学生架起思想、知识与能力的桥梁,促进学生物理解题能力的提升.

1 整体法和隔离法的基本思想

1.1 选择研究对象

开始物理解题的第一步则是选择适合的研究对象,整体法和隔离法即是根据研究对象的不同自然演变形成的两类解题方法.在高中阶段的众多物理问题中,研究对象选择的差异将会直接影响学生求解问题的繁简度[1].因此,如果同学们能够选择一个正确的对象,采取合适的方法一定会使自己的计算更加简单,反之则会使问题复杂化.因此,在解决对应的物理问题时,同学们要根据具体问题情境合理选择使用整体法或者隔离法.

1.2 整体法

整体法即是对整个系统进行研究分析或对整个物理过程进行研究探讨.简单来说,如果我们求解的物理问题只涉及一个物理过程或这一系统的起始状态和末端状态,则我们可以通过将这一整个过程或整个系统视为一个研究对象,利用整体法求解,但是如果求解的问题属于该过程中间的状态量,则不能使用整体法[2].

1.3 隔离法

隔离法即是将研究对象从其所处的系统或环境中单独拿出来进行研究.这个对象可以是一个物体也可以是某段过程.比如在求解系统的内力时,我们可以将该对象从这一系统中分离出来,再使用隔离法分析求解.同样的,如果求解对象是某一过程中间的一个状态量,我们就可以将一个物理过程从其全过程中单独隔离,并且逐步分析[3].

高中阶段,整体法和隔离法广泛地应用在受力分析、动量定理、机械能守恒这些物理问题中.大部分情况下,在解答一个问题时,需要多次选取研究对象,因此,我们考虑将整体法和隔离法交叉使用,通常先整体后隔离.

2 整体法和隔离法的应用实例分析

2.1 整体法和隔离法在受力分析中的应用

比如以下一个经典模型:如图1,木块质量为m1、m2,三个木块均静止,讨论三角形木块与粗糙水平面之间的摩擦力大小;

图1 整体法与隔离法应用

在此模型中,部分同学会先隔离m1、m2以及该三角形木块,并对这三个木块进行受力分析.根据牛顿第三定律以及物体平衡的条件,再快速确定三角形木块与粗糙水平面之间的摩擦力,以求解原问题;这一思路是可行的,但求解过程以及受力分析较复杂,容易将问题复杂化.因此,我们考虑将m1、m2和三角形木块视作一个不规则的整体,并即将这一整体看作研究对象.显然这一研究对象在竖直平面上只受重力、支持力,水平面上不受其他外力作用,因此,该三角形木块与粗糙水平面间的摩擦力大小为0.

例1如图2在光滑的水平地面上有三个质量相等,且均为M的木块分别为abc,形状相同的a、c两木块之间用轻绳连接.现用水平恒力F作用于木块b上使三者开始一起做匀加速运动.在运动过程中将一块橡皮泥粘在某一个木块上,已知系统仍在做加速运动,且始终没有相对滑动,则在粘上橡皮泥并达到稳定的过程中,则下列说法错误的是( ).

图2 例1题图

A．无论橡皮泥是粘在哪块木块上,系统的加速度一定减小

B．若橡皮泥是粘在a木块上,绳的张力减小,ab间摩擦力不变

C．若橡皮泥是粘在b木块上,绳的张力和ab间摩擦力一定都减小

D．若橡皮泥是粘在c木块上,绳的张力和ab间摩擦力一定都增大

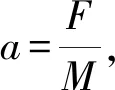
2.2 整体法和隔离法与牛顿第二定律的综合应用

在分析系统内各个物体加速度不相同而又不需要求系统内物体间的相互作用力时,我们可以使用整体法和隔离法来求解有关牛顿第二定律的相关问题,从而大大简化数学计算[4].在使用整体法和隔离法时,要把握题干中关键的两点:一是题目只要求分析系统所受到的外力,二是要求分析系统内各个物体的加速度的大小和方向.

例2如图3,已知物体A和B放在倾斜角度为37度的斜面上,若A和B的质量分别为2 kg和2.5 kg,且A、B之间的动摩擦因数为μ1=0.5,B与斜面之间的动摩擦因数μ2=0.4.将能固定物体A的绳子沿水平方向固定于斜面顶端,用平行于斜面向下的拉力F将物体B匀速拉动.且在此过程中物体A始终保持静止状态,试求:

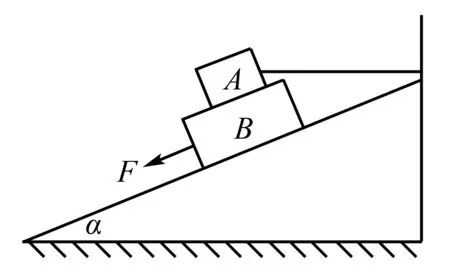
图3 例2题图

(1)物体A和B之间滑动摩擦力的大小;

(2)拉力F的大小.

答案:(1)40 N (2)29 N.

2.3 连接体中的整体法和隔离法

连接体问题是高中物理动力问题中的常见题型.针对连接体问题需要分情况灵活选择使用整体法或者隔离法,如果可以用整体法全局分析,我们应该优先采用整体法,控制研究数量、未知量以及方程数量,从而简化自己的计算[5].例如不需要考虑系统的物体间相互作用的内力时.当然,不是所有的连接体问题都可以使用整体法得到最终结果,大部分情况下,我们考虑使用整体法与隔离法相结合的思路来求解相关问题.

例3如图5所示,质量均为m,且可视为质点的两个木块A、B之间用质量为2m,长为L的水平杆C相连,水平杆与地面平行但不接触地面.该系统以水平速度v沿光滑水平轨道向右做匀速运动,然后进入P点右侧粗糙的水平面,且A、B两木块与P点右侧的动摩擦因数都是μ,C与A、B间作用力的竖直分量相等.求:

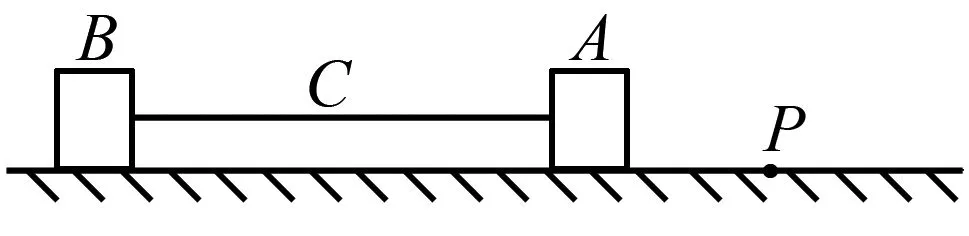
图5 例3题图

(1)在A过P点瞬间,A、C之间和B、C之间弹力的水平分力之比是多少;

(2)B在P点右侧滑行的距离.(设v2>μgL)

A受到的滑动摩擦力大小为f=μFN=2μmg

根据整体法,将A、B、C整体做为研究对象,由牛顿第二定律得f=4ma

可得a=0.5μg

设A、C之间和B、C之间弹力的水平分力大小分别为F1和F2.

再使用隔离法,以A为研究对象,由牛顿第二定律得:f-F1=ma

解得:F1=1.5μmg

同理,以B为研究对象,由牛顿第二定律得:

F2=ma

解得:F2=0.5μmg

则F1∶F2=3∶1

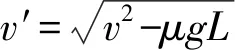
B过P点后,以A、B、C整体为研究对象,由牛顿第二定律得μ(m+m+2m)g=4ma′

可得a′=μg

设B在P点右侧滑行的距离为x,则

0-v′2=-2a′x

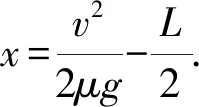
总的来说,整体法和隔离法作为高中物理动力学问题的解题过程中常用到的方法,同学们一定要注意日常积累.在平常的练习过程中,着重对各个知识点的把握和方法的使用,保证自己在考场上游刃有余.