点差法与圆锥曲线第三定义的应用举例

尹伟云

(贵州省仁怀市周林高中,贵州 仁怀 564599)

圆锥曲线中的中点弦和直径问题是高考经常考查的对象．在某些与中点及直径有关的相交弦问题中,利用点差法或圆锥曲线第三定义可快速得到两直线的斜率之积,尤其是在小题中,直接利用结论求解,可大大地节省解题时间．下面就这些问题进行探讨．

1 点差法的原理

1.1 点差法在椭圆中点弦问题中的应用

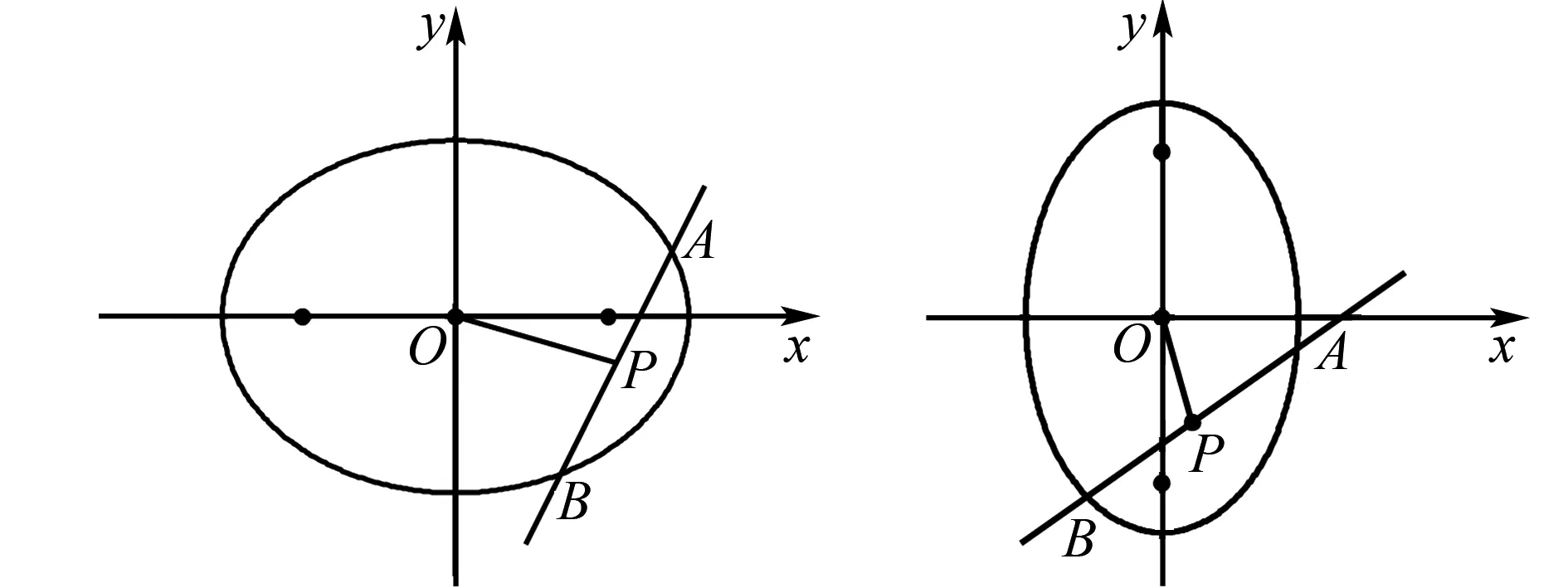
图1 椭圆焦点在x轴 图2 椭圆焦点在y轴

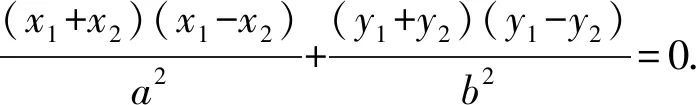
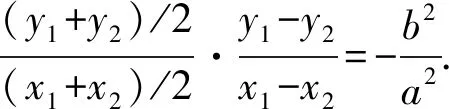
如图2,当椭圆的焦点在y轴上时,同理得

1.2 点差法在双曲线中点弦问题中的应用

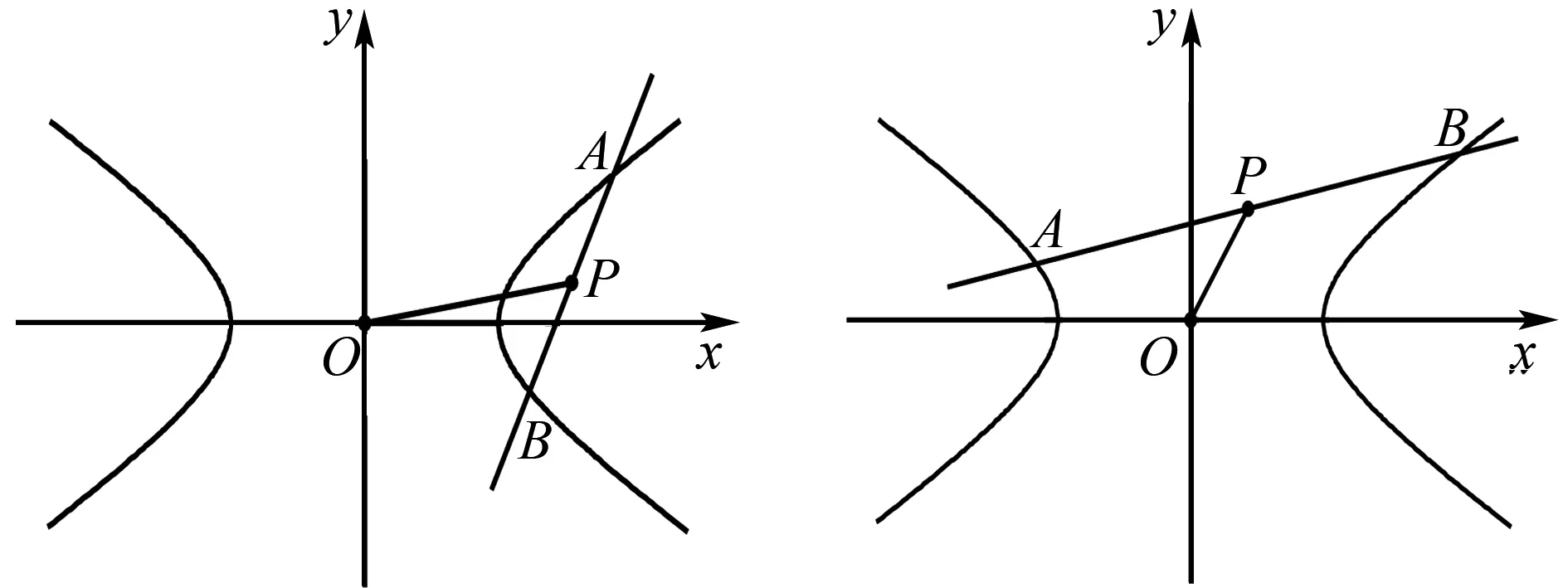
图3 双曲线中点弦问题 图4 双曲线中点弦问题

根据结论1和结论2,容易知道椭圆、双曲线中点差法的统一公式:

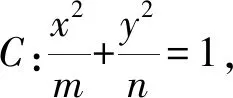
1.3 点差法在抛物线中点弦问题中的应用

图5 抛物线中点弦问题

即得y0·kAB=p．

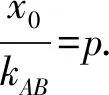
2 圆锥曲线的第三定义

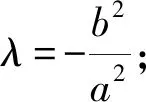
由上知,λ=e2-1,其中e为对应轨迹的离心率．

将圆锥曲线第三定义进行推广,得到如下结论:

图6 结论4图

当椭圆的焦点在y轴上时,有

证法1 设P(x0,y0),A(x1,y1),则B(-x1,-y1),从而直线PA,PB的斜率之积为

证法2取AP的中点M,连接OM,由点差法,得

当椭圆的焦点在y轴上时,同理可证

图7 结论5图

当双曲线的焦点在y轴上时,有

证法1设P(x0,y0),A(x1,y1),则B(-x1,-y1),

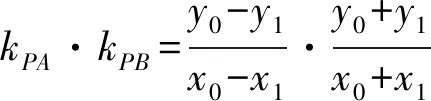
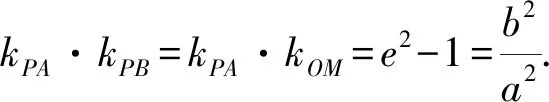
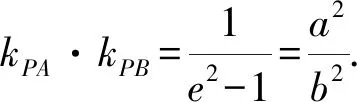
3 实例分析

解析由题意知,直线AB与l互相垂直,所以kAB·kl=-1,得kAB=-m．

设线段AB的中点为M(x0,y0),由点差法,得

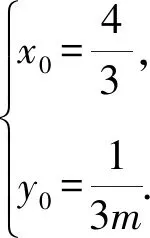
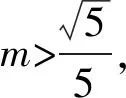
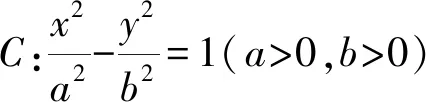
解析设线段MN与其垂直平分线交于点P,连接OP,如图8．

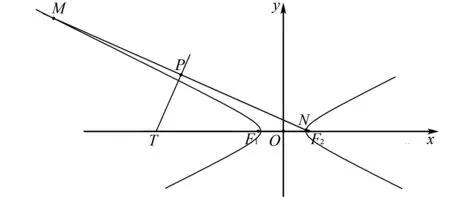
图8 例2解析图

①

②

又由①得

解得y0=5b.

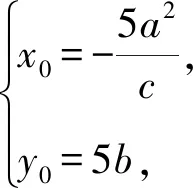
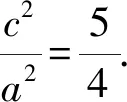
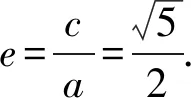
图9 例3解析图

解得x0=4kAB=4.

即得kAB=1,从而y0=4+m.

由垂径定理,得AB⊥MI.

所以kAB·kMI=-1.

x2-8x-20=0.

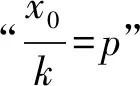
解析在椭圆C中,由椭圆第三定义,得

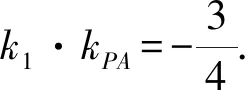
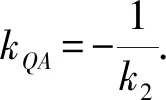
所以kPA=kQA.

又直线PA与QA共点A,所以A,P,Q三点共线．

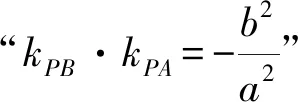
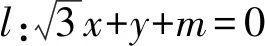
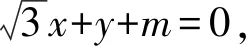
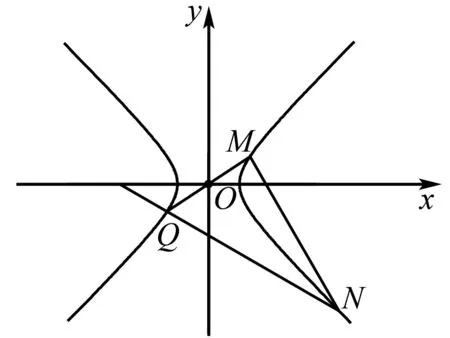
图10 例5解析图

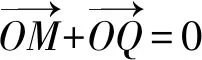
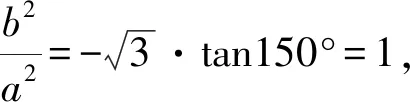
所以双曲线C的渐近线方程为y=±x．

评注本题由双曲线第三定义快速得到关于a,b的齐次分式与kMN,kQN的等量关系,再由直线MN的倾斜角及条件中的已知角求得kQN,从而得到关于a,b的齐次方程,即得双曲线的渐近线方程．利用双曲线第三定义解题,首先要寻找过双曲线中心的相交弦,其次在双曲线上另找一点,向弦两端点引直线,再将这两直线的斜率转化为可求的量．