全叶高合成双射流对大折转角扩压叶栅的影响
朱寅鑫,彭文强,罗振兵,康赢,赵志杰,程盼,刘杰夫
国防科技大学 空天科学学院,长沙 410073
随着航空推进装置的迅猛发展,航空发动机朝着更高推重比的方向发展,这也要求压气机设计技术向高效率、高压比方向发展[1-2]。例如美国现在对航空发动机的研制目标之一就是在高效的基础上实现发动机的大推力和高推重比[3]。大折转角叶型可有效提升叶片载荷,从而提升叶栅单级压比。随着叶片负荷提升,叶栅流动损失加剧,扩压能力减弱。因此,采用合理的流动控制技术抑制流动分离,改善大折转角扩压叶栅的性能是十分必要的[4]。常见的流动控制技术包括涡流发生器[5]、叶表开缝[6]、边界层吹气[7]、射流式涡流 发 生 器[8]、边 界 层 抽 吸[9-10]、等 离 子 体 激励[11-13]等。
其中,合成射流类控制技术相较其他控制技术,能够在不增加额外管路的情况下,仅通过改变输入电参数即可改变射流参数。合成射流激励器具有驱动机构复杂性小、能耗低的特点[14-15]。国内外许多学者开展了关于合成射流在扩压叶栅的应 用 研 究。Zander[16]和Gmelin[17]等 在 来 流 马 赫数为0.07 的扩压叶栅的叶表和端壁上施加合成射流,实验和数值计算结果表明,总压损失系数减少近10%。Zheng 等[18]将合成射流应用于环形叶栅,总压损失系数降低27.5%。秦勇等[19]在来流马赫数为0.67 的高速扩压叶栅表面施加合成射流,数值计算结果表明,总压损失系数可降低19.8%。蔡乐等[20]通过数值计算开展对某低反动度叶栅的合成射流控制研究,发现合成射流可有效改善大尺度分离涡结构,并简要研究各激励参数的影响。Giorgi 等[21]通过大涡模拟得出结论:合成射流控制叶表分离的关键在于射流的非定常特性与掺混效应。Benini 等[22]对合成射流在跨声速环境中对激波/边界层干扰的控制有效性进行探索性研究。合成双射流是由合成射流改进而来,如图1 所示,激励器为单膜双腔结构,通过压电膜片将腔体分为2 个部分[23]。该构型解决了合成射流激励器能量利用率低、易压载失效的问题,从而进一步提升激励器的流场控制能力[24]。在对于控制机翼流动分离的数值计算和实验研究中发现:相比于合成射流,合成双射流的2 个出口交替处于“吹气”和“抽吸”状态,可有效增大失速攻角范围,进一步延迟机翼的流动分离[25-26]。合成双射流环量控制技术已成功应用于无人机中[27],其对外流场的控制能力得到验证。

图1 合成双射流激励器示意图Fig.1 Sketch of dual synthetic jet actuator
上述研究表明,合成射流类控制能改善扩压叶栅性能,减少流动损失。因此,研究合成双射流能否进一步提升控制效果是十分有意义的。此外,在关于大折转角扩压叶栅的研究中,叶栅工作环境多为低速不可压流场,本文将针对来流马赫数为0.3 的工况开展数值研究。本文以大折转角高速扩压叶栅为研究对象,探究合成双射流的射流位置、动量系数、激励频率对叶栅流动损失控制的影响。
1 研究对象与方法
1. 1 叶栅与合成双射流
针对轴流压气机静子平面叶栅,本文开展合成双射流控制叶栅损失的研究。当静子叶型折转角较大时,负荷较高,有必要通过一定的流动控制手段改善性能,减少分离损失。叶型的弦向厚度基于NACA65-010 叶型数据设计,NACA-65 系列叶栅被广泛应用于轴流压气机。叶型沿弦向的厚度分布与NACA65-010 相同,基于特定函数垂直于弦向偏移,函数为
叶栅设计来流马赫数为0.3,表1 给出叶型几何参数,几何折转角为72°。

表1 大折转角叶栅几何参数Table 1 Geometry parameters of high-turning cascade
合成双射流激励器的射流槽布设在叶片吸力面表面。图2 给出合成双射流的参数示意图。本文分别研究了合成双射流位置Δl、动量系数Cμ、频率参数f 的影响。射流位置Δl 是射流槽前缘的轴向相对弦长位置。射流槽宽度H 为其前后缘弦向距离,固定为1 mm。射流角度α 是射流出口方向与该处叶片表面切线的夹角。

图2 合成双射流控制方案示意图Fig.2 Sketch of control scheme by dual synthetic jets
1. 2 数值方法
利用软件Fluent 对可压缩非定常Navier-Stokes 方程进行求解。计算域是一个包含单个叶片的叶栅通道。流场为亚声速环境,叶栅尾迹涡结构复杂,为避免计算域进出口对叶栅前后数据的测量干扰,计算域入口在栅前1.5 倍弦长处,出口在栅后2.5 倍弦长处。为减少边界条件的影响,实际监测进出口参数的截面与计算域进出口边界的距离为10%轴向弦长。采用HOH 型结构化网格,对叶片表面、前后缘和端壁附近的网格进行局部加密,确保y+<1。图3 给出计算域网格。时间离散为二阶后向欧拉法,湍流模型为RNG k-ε模型。进口总压为104 kPa,总温为300 K,进口气流角55°,出口静压100.1 kPa,通过微调出口背压使得进口马赫数为0.3。为提高计算效率,先进行定常计算,将定常解作为非定常计算的初始值。在非定常计算中,时间步为1×10-5s,每个时间步长迭代20 次。通过监测出口压力判定计算是否收敛,收敛后再计算200步作为最终计算结果。

图3 叶片通道计算域网格Fig.3 Computational grid of blade passage
目前高负荷大折转角叶栅的公开数据较少。如图4 所示,通过比较折转角较小的NACA1210叶型表面速度系数的实验结果[28-29]和数值计算结果验证数值计算方法的可靠性。其中,q 为当地动压,q0为来流平均动压。结果表明,数值方法对叶表参数变化趋势预测准确。

图4 数值计算方法验证Fig.4 Validation of numerical calculation method
合成双射流激励器的工作原理是通过腔体内的膜片振动使得腔体内压力发生周期性变换,从而实现对主流工质的吹除与吸入。利用非定常压力入口条件,模拟合成双射流激励器膜片振动效应对流场的影响。假设激励器出口总压为
式中:Pj为一个周期内压力波动幅值;比热比γ 设为1.4;Maj为需要的射流峰值马赫数;f 为激励频率;φ 为初始相位角,上游射流槽设置为0,下游射流槽设置为π;t 为时间。无量纲激励频率f*定义为
式中:V∞为叶栅的来流速度;c 为叶栅弦长。激励幅值通过动量系数表征:
式中:H 为射流槽的宽度;Vjet为射流峰值速度。合成双射流作为零质量射流并不会额外引入工质,且每一时刻2 个射流槽的吹吸状态的相位差为π,即一个射流槽在吹气时另一个射流槽在吸气,故假定瞬时主流流场工质无变化。瞬时叶栅总压损失为
式中:P1*和P2*分别为进出口的总压;P1为进口的静压。本文以一个周期内的总压损失系数时均值作为评判流场损失的参数,定义为
其中:m1(t)是来流质量流量,由于合成双射流的非定常效应会影响进口条件,故需考虑来流质量流量的变化。
选用4 种不同网格数的网格开展网格无关性验 证,网格总数分别为1.07×106、1.45×106、1.97×106、2.65×106。在来流马赫数为0.3,进口气流角为55°的条件下使用这4 个网格进行计算。得到的总压损失分别为22.02%、21.43%、21.18%、20.96%。本文使用非定常计算进行参数研究,计算周期长,结合计算效率,选用网格数为1.45×106的网格。
2 合成双射流对叶栅的影响
2. 1 叶栅特性
对于常规的扩压叶栅,在小冲角时能够保证叶高中部为附着绕流,只有在大冲角时会出现吸力面分离。通过图5 给出的壁面极限流线可发现,在该大折转角叶栅中,叶片后缘吸力面表面无附着流。通过吸力面表面流线可发现,分离结构为明显不对称结构。一侧出现跨度超过半叶高的分离泡,端壁出现回流区,是典型的闭式分离;另一侧端壁无回流区,为开式分离。由于端壁、吸力面均出现回流区,可初步定性判定角区发生失速[30-31]。此外,叶栅的扩散参数D 定义为

图5 原始叶栅的壁面极限流线Fig.5 Limited streamlines of baseline cascade
式中:i 为入射角;ξ 为安装角;θ 为几何折转角;s 为栅距。
经计算发现,该叶栅的扩散参数D>0.405,根据Lei 等[32]提出的轴流压气机角区失速判定准则,该叶型流场中会形成较大尺度的以闭式分离结构为特征的端壁回流,即发生角区失速。观察流线可发现,由于叶栅折转角过大,即便在0°攻角下都处于失速状态,出现全展向的流动分离,甚至由于一侧端壁流动分离发展得较为充分,进而抑制了另一侧的流动分离。Nerger 等[33]在实验中发现类似的现象。可见叶型几何折转角对流场结构有显著影响。
本文通过涡量Ω 和Q 准则识别流场中的旋涡结构[34]。图6 给出叶栅通道内的涡结构,可发现,吸力面表面分离涡尺度大,在下游发生集中脱落。可推测吸力面分离涡对叶栅通道内堵塞影响严重。

图6 原始叶片通道内的涡结构(Q=2×106)Fig.6 Vortex structures in blade passage of baseline cascade (Q=2×106)
图7给出流向涡量分布。结合图6,轴向弦长位置<20%时,马蹄涡沿流向发展,涡量与附面层涡量处于同一量级。在25%轴向弦长处,吸力面分离涡开始发展,虽然涡尺度不大,但是涡量强度较大。在40%轴向弦长处,吸力面分离涡发展较为充分,并向上游抬升,逐渐堵塞通道。随后吸力面分离涡强度衰减。

图7 叶片通道内不同截面处的涡量云图Fig.7 Contours of vorticity magnitude at different cross-sections in blade passage
图8给出流向总压损失系数分布。马蹄涡会在角区附近形成局部高损失区域,由于尺寸较小,对于整个通道影响较小。随着吸力面分离涡的发展,高损失区域从角区发展并沿流向累积,逐渐向整个叶栅通道扩张。高损失区域分布形态与吸力面分离涡形态相近。

图8 叶片通道内不同截面处的总压损失系数云图Fig.8 Contours of total pressure loss coefficient at different cross-sections in blade passage
不对称的流场结构会导致叶片表面的载荷分布不对称,由图9 可看出,不同叶高处的静压分布区别较大,叶栅吸力面表面静压分布差异显著。因此可推断,对于大折转角叶栅而言,若能将流场的非对称流动分离结构改变为对称结构,意味着端壁分离减弱,进而有效改善叶栅性能及其载荷分布。

图9 叶片表面无量纲静压分布Fig.9 Distribution of dimensional static pressure on blade surfaces
2. 2 射流槽位置的影响
本节在相对轴向弦长5%~64.4%范围内共设置8 个不同射流位置合成双射流控制方案。由于叶片尾缘较薄,开设射流槽对叶片强度影响较大,故不作研究。各工况中,进口气流角为55°,射流动量系数Cμ为0.65%,射流角度为30°,无量纲激励频率f*为0.588。图10 给出不同射流位置下的叶栅总压损失系数。可以发现,合成双射流的位置存在明显的有效激励范围。对于特定工况,当射流槽位置为28.8%相对轴向弦长时,叶栅总压损失系数显著下降。可见合成双射流可有效减少大折转角叶栅的流动损失。当射流槽位于36.6%轴向弦长处时,控制效果最好,相比无控制状态,总压损失系数降低54.8%。当合成双射流位置偏离最佳控制位置时,合成双射流对叶栅性能的改善能力减弱。射流槽位置过于靠前时,反而会增大叶栅的损失。

图10 不同合成双射流位置的叶栅总压损失系数Fig.10 Total pressure loss coefficients of cascade with different positions of dual synthetic jets
通过图11 中典型工况的涡结构可发现,合成双射流可显著改变流场结构,在吸力面分离涡充分发展前布置射流槽,合成双射流可有效将非对称流场结构变为对称流场结构。在叶栅的13.1%轴向弦长处,前端流场结构稳定,尚未发生明显分离,若在此处施加控制,合成双射流会在吸力面表面提前形成涡。当激励位置处于有效控制位置时,随着射流槽位置接近最佳控制位置,吸力面分离涡流向尺度缩短,高度降低。当激励位置靠后时,射流槽上游已形成全叶高的流动分离,此时合成双射流已无法改变流场结构,但合成双射流减小了尾迹脱落涡的尺度,叶栅下游流场结构有一定改善。可见,合成双射流对大尺度分离涡有明显的破碎效果,破碎的分离涡结构有序地向下游周期性脱落,并向通道下游传递。图12 为Δl=36.6%时,叶展中部的流线,可发现合成双射流将大尺度的分离涡变为规律脱落的小涡。

图11 不同合成双射流位置叶栅通道内的涡结构(Q=2×106)Fig.11 Vortex structures in blade passage with different positions of dual synthetic jets (Q=2×106)

图12 Δl =36.6%时叶展中部的流线Fig.12 Streamlines in middle of cascades for Δl =36.6%
图13给出各工况叶栅通道内的总压损失系数分布。当射流位置在13.1%轴向弦长时,原始叶栅吸力面分离涡尚未形成,边界层附近流动损失较低。此时施加合成双射流反而会增大边界层内的损失,合成双射流引发的边界层损失会逐渐向下游累积。此外,该位置距离原始叶栅的高损失区较远,对下游流场影响有限。因此在该位置施加控制会增大叶栅损失。然而在前端施加合成双射流能够有效使流场变为对称结构。当射流槽位于有效激励范围时,原本吸力面分离涡引发的流动损失被抑制,射流槽下游吸力边界层损失减少,叶栅通道内高损失区域的高度下降。射流槽位于36.6%轴向弦长处,尾缘附近叶展中部的损失显著下降。当处于有效范围之内时,不同射流槽位置下流场结构相似,均可达到较好的控制效果。当射流槽位置靠后时,射流槽上游非对称吸力面分离涡已经充分发展,此时施加控制已无法改变流场结构,但合成双射流的周期性吹吸效应仍可以影响上游流场,一定程度上减弱射流槽上游的流动损失。

图13 不同合成双射流位置下叶片通道内的总压损失系数云图Fig.13 Contours of total pressure loss coefficient in blade passage with different positions of dual synthetic jets
比对2.1 节图7 中初始叶栅不同弦向的涡量分布,可以发现在吸力面分离涡还没充分发展的位置,流场损失较小,合成双射流对该处的流场无改善能力。随着分离涡向下游发展,其强度和范围都在增大,在该处施加合成双射流能有效减弱吸力面分离涡引发的流动损失,并改善流场结构。在叶栅后段,涡强度衰减,此时合成双射流对强度已经衰减的涡影响有限,且上游非对称流场结构已经形成,吸力面分离涡造成的损失已经累积,合成双射流无法消除上游形成的不利影响。因此可推断,涡充分发展的区域是有效控制区域。
2. 3 动量系数的影响
选取合成双射流的射流槽位于36.6%轴向弦长处,射流角度30°,无量纲激励频率f*为0.588,选取不同的射流动量系数。
图14给出不同动量系数下的叶栅总压损失系数。可以发现,其余参数不变,各动量系数均可降低叶栅流场损失。合成双射流的激励幅值存在有效阈值,约为0.29%。射流动量系数极小时,叶栅损失略微下降,流动控制效果不显著。当射流动量系数达到该阈值,控制效果显著提升。可见合成双射流必须具备足够的动量与边界层低能流体发生动量交换。而射流动量系数进一步增大会导致流场损失缓慢上升。

图14 不同动量系数的叶栅总压损失系数Fig.14 Total pressure loss coefficients of cascade with different momentum coefficients
图15给出典型工况下的总压损失系数分布。可以发现,即使在动量系数较小时,流场结构也会变为对称结构。结合2.2 节对控制位置效果的分析可推断,这是由于射流槽处于最优控制位置,合成双射流微弱的扰动即可促进流场形态的改变。当控制位置在有效范围内时,合成双射流的控制效果对动量系数限制较小。进一步验证流场结构的改变是改善大折转角叶栅性能的关键。当动量系数超过阈值后,叶展中部的损失减小,流场结构进一步改善。比较图13(c)与图15(b),可发现随着动量系数增加,吸力面上方的损失逐渐增加。

图15 不同动量系数的叶栅通道内的总压损失系数分布云图Fig.15 Contours of total pressure loss coefficient in blade passage with different momentum coefficients
图16给出射流槽附近展向涡量分布。可以发现合成双射流激励器形成的射流进入主流流场后发生偏转,在射流槽前缘形成逆向涡,与主流发生剪切作用。随着射流动量系数的增加,射流偏转程度减弱,合成双射流对边界层的射流与抽吸作用增强,剪切作用加强,不可避免地增加黏性耗散,从而引入了额外的损失。

图16 不同动量系数的射流槽附近展向涡量云图Fig.16 Contours of spanwise vorticity near jet slots with different momentum coefficients
图17给出叶片通道内的流向涡量分布。可以发现合成双射流会影响在角区附近的吸力面流向涡。吸力面流向涡与端壁附近的涡旋向相反,影响了原始叶栅端壁附近的涡演化。射流动量系数为0.65%时,旋向相反的2 个涡在端壁附近相互作用,端壁附近的涡量减弱。当射流动量系数为1.30%时,合成双射流吸力面流向涡强度较大,减弱端壁附近的涡强度,同时带动端壁附近的涡向叶栅通道移动,增大堵塞效应。

图17 不同动量系数的叶片通道内的流向涡量云图Fig.17 Contours of streamwise vorticity in blade passage with different momentum coefficients
2. 4 激励频率的影响
本节给出不同激励频率对叶栅流动损失的控制效果(结合目前合成双射流常用的压电陶瓷振子特性,选取激励频率f 分别为200、400、600、800、1 000、1 200 Hz)。各工况中,进口气流角为55°,射流位置为36.6%相对轴向弦长,射流动量系数Cμ为0.65%,射流角度为30°。作为典型非定常流动控制手段,合成双射流激励器的一个优势在于仅通过调节电源频率即可设置不同的合成双射流激励频率,调节范围广,具有较大的灵活性。选取合理的频率能进一步提升控制效果。
图18 给出叶栅总压损失系数随激励频率的变化关系,可发现存在最佳频率范围,约为600~1 000 Hz。当其余参数都处于较优范围内,各激励频率都可保持较好的控制效果。若在最佳频率范围内,合成双射流控制效果得到进一步提升,叶栅损失下降。

图18 不同激励频率的叶栅总压损失系数Fig.18 Total pressure loss coefficients of cascade with different excitation frequencies
图19 给出不同激励频率叶栅通道内瞬态的Q 等值面图,可发现合成双射流的周期性吹吸会影响流场特性。合成双射流能打碎吸力面表面形成的分离涡。随着激励频率的增大,吸力面分离涡的流向尺度缩短,并使得下游的尾迹涡更加细碎。合成双射流改变吸力面表面流场参数的变化,使得其随着激励频率的改变而改变,促进分离涡发生周期性脱落,受迫振荡效应明显。
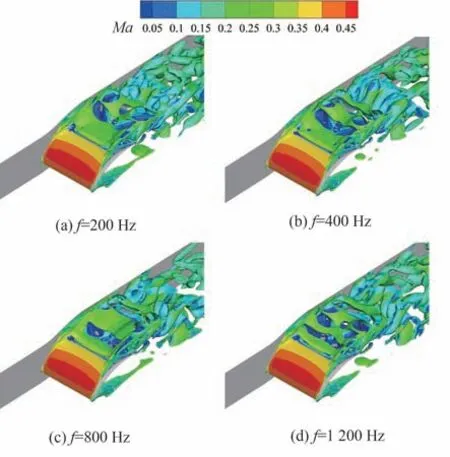
图19 不同激励频率叶栅通道内的涡结构(Q=2×106)Fig.19 Vortex structures in blade passage with different excitation frequencies (Q=2×106)
3 结 论
本文以三维轴流压气机大折转角平面扩压叶栅为研究对象,提出一种利用合成双射流改善叶栅流场损失的控制方法。通过数值计算分析合成双射流位置、动量系数、激励频率的影响,得出如下结论:
1)大折转角叶栅叶片负载大,在0°攻角即处于失速状态,吸力面表面形成非对称分离涡。合成双射流可有效将叶栅流场变为对称结构,从而降低流动损失,总压损失系数最大降低54.8 %。
2)合成双射流的射流槽位置是影响控制效果的关键因素。在原始叶栅的分离涡强度较大且充分发展的位置施加控制,效果最好。过早布置合成双射流会增大流场损失,总压损失系数大于无控制状态。在分离涡已充分发展且强度减弱的位置施加控制效果较差,无法改变非对称流场结构但能改善叶栅下游尾迹涡结构。
3)射流动量系数和激励频率是重要控制参数。射流动量系数存在有效阈值,合成双射流必须具备足够的动量与边界层低能流体发生动量交换。过大的射流动量系数使得合成双射流与主流流场的剪切作用增强,减弱控制效果。当其余控制参数都处于较优范围内时,各激励频率都可保持较好的控制效果。
本文研究吸力面合成双射流参数对叶栅损失控制的影响。吸力面的合成双射流可有效减小叶栅表面的流动损失,但角区损失依旧较大。结合本文结论,可推测在端壁施加合成双射流有可能获得较好的控制效果,且端壁与吸力面的合成双射流组合控制则有可能弥补单个控制方案的不足并进一步提升控制效果。下一步将研究端壁合成双射流参数对控制效果的影响,并尝试开展组合优化控制研究。

