基于多元回归模型的临床工程人员配置方案研究

沈 慧，续大伟

临床工程师是将临床医学基础、工程和管理等知识应用于医疗保健服务中，从而支持和改善患者治疗和护理的专业人员[1]。 随着现代医疗服务对相关医疗设备的依赖程度越来越高，医疗机构对临床工程人员的需求也越来越大[2~4]。 中国医师协会临床工程师协会在2020年发布的《中国临床工程师职业发展规划研究报告》中指出，与其他专业技术人员相比，临床工程人员的配置数量少[5]。 同年，在《三级综合医院评审标准》中对于医学装备的管理，也明确提出了合理配置临床工程人员的要求，但迄今为止中国还没有广泛接受或准确的模型来确定临床工程部门人员的配置数量。医疗机构中临床工程人员配置数量取决于人员职责的范围和深度，最常见的人员配置标准是医院的业务发展，床位数量、医疗设备的数量和价值及工作量等实际情况[6~9]，而没有考虑各配置标准指标共同影响的结果，势必会造成人员配置的不均衡[10]。 笔者采用横断面调查的研究方法，获取医疗机构及其临床工程部门的基本特征，通过多元回归分析探讨临床工程人员配置水平的影响因素，深入了解各决定因素对临床工程人员配置数量的影响程度，得出医疗机构临床工程人员配置数量的预测模型。

1 材料与方法

1.1 实验材料

以J 省三级以上医疗机构临床工程部门为调查对象，综合考虑临床工程人员配置标准[10~13]，结合中国医师协会开展的“中国临床工程师执业情况调研”的基础上[5]，实验重新设计了临床工程部门人员配置需求的调研问卷，包括医疗机构的基本情况（如医院等级、开放床位数、出院病人数、医疗设备固定资产总值、医疗设备数量、年度内部维护成本和年度外部维护成本等），临床工程部门的基本情况（如临床工程人员数量、是否进行外包托管和技术工作时长等）。并于2021年11月至2022年3月采用“问卷星”的方式在线进行横断面调查。

1.2 方法

1.2.1 模型的建立

对调查问卷的基本信息进行梳理和分组，以临床工程人员配置数量为因变量，技术工作时长、开放床位数、设备数量、出院病人数和服务率为自变量，采用逐步向前回归法建立多元回归方程，首先引入开放床位数变量构建模型1，然后通过引入其余变量设备数量和技术工作时长构建模型2。 通过确定当引入或从模型1 中删除新变量时常数项β 是否发生显著变化，从而评估新变量对模型2 的影响。

其中技术工作时长、开放床位数、设备数量、出院病人数、服务率和临床工程人员数量都是不需要特殊运算转换的数值型变量。由于结果变量配置数量相对于设备数量、 出院病人数和技术工作时长数值较小，同时这些变量与结果变量临床工程人员配置数量的离散图呈现持续增加的趋势[14]，为了消除异方差，需对各自变量进行对数转换。

1.2.2 统计学方法

所有的统计分析均使用SPSS 26.0 进行，检验的显著性α 水平为设定P＜0.05（双侧）。

1.2.2.1 相关性分析 各自变量之间的相关性分析采用Spearman 相关分析。 当该自变量与其他自变量之间的Spearman 秩相关系数均高于0.8 且P 值具有统计学意义时，意味着该对自变量之间不是完全独立的，具有共线性，即该自变量不纳入多元回归模型中。

1.2.2.2 模型的检验 检查多元回归方程模型的所有假设（变量之间的共线性，残差的自相关性，残差的正态性） 及模型的预测精度。 通过方差膨胀因子（variance inflation factor，VIF）检验共线性，若VIF ＞5表示共线性，则需将该变量从模型中剔除[14]。 残差的自相关性采用Durbin Watson 检验[15]，在k=3，α=0.01时，Durbin Watson 的临界值du= 1.60。 使用Shapiro Wilk 正态分布检验残差的正态性，以P＞0.05 表示呈正态分布。 采用解释方差（即R2）检验多元回归方程模型的预测精度，当模型的R2＞0.7 时，表明模型具有较强的预测能力。

2 结果

2.1 问卷调查结果

累计给60 家医疗机构发放问卷60 份，回收有效问卷52 份， 问卷的有效回收率为86.67 %。 采用G*Power 3.1.9.7 软件估算样本量[14]，鉴于该领域以往实证研究的稀缺性和有效性，为了保守起见选择中等效应量。在效应量为0.3 时，为了达到0.8 的统计功效（在α=0.05 时），评估得到的样本量为29 个，即至少需要29 个临床工程部门， 说明实验研究的样本量满足调查要求。如表1 所示为J 省三级以上医疗机构和临床工程部门的基本情况，从表中可以看出各变量的标准偏差较大，说明所调研的医疗机构具有多样性和代表性。 其中92.31%以上的记录表明医疗机构采用基于内部模式的临床工程模式，此变量没有统计测量标准差数据，因此多元回归分析模型中没有包括临床工程部门模式变量。

表1 医疗机构和临床工程部门的基本情况Tab.1 Basic information of medical institutions and clinical engineering departments

2.2 相关性分析结果

临床工程人员数量和技术工作时长、开放床位数、设备数量、出院病人数、服务率之间的相关系数矩阵如表2 所示，Spearman 秩相关分析显示临床工程人员数量与技术工作时长、设备数量、开放床位数及出院病人数呈显著相关性， 其相关系数分别为0.840、0.846、0.890、0.940，且P＜0.01。 但出院病人数与技术工作时长、设备数量及开放床位数之间的Spearman 秩相关系数大于临界值0.8，因此未将出院病人数纳入多元回归模型。而临床工程人员数量与服务率无相关性（r=0.212，P=0.131），故也未将服务率纳入多元回归模型。

表2 各自变量之间的Spearman 秩相关分析Tab.2 Spearman rank correlation analysis in independent variables

2.3 多元回归模型的结果

表3 为模型的多元回归分析结果， 与模型1 相比， 模型2 的决定系数 （R2=0.837） 增加了20.2%（△R2=0.202）。 因此采用模型2 来分析临床工程人员配置数量的影响因素。从表3 中进一步看出技术工作时长、开放床位数和设备数量与临床工程人员配置数量在统计学上呈现显著正相关 （β = 12.782，P =0.001；β=3.339，P=0.009；β=2.346，P=0.001）。得到的多元回归方程为：

表3 回归系数及显著性检验Tab.3 Results of regression coefficient and significance test

2.4 多元回归模型的检验

如表3 所示模型2 的ANOVA 检验的F 为82.009，P＜0.001， 表明所建立的多元回归方程模型具有统计学意义。多元回归方程模型的决定系数R2=0.837（＞0.7），说明拟合度较好，即模型的预测精度较高。 Durbin Watson 检验统计量d = 1.711 ＞du=1.60，可知该模型中残差不存在自相关[15]。 表4 共线性统计及共线性诊断结果表明，技术工作时长、设备数量和开放床位数的VIF 均小于5， 条件指数均小于30，表明模型不存在多重共线性，模型回归有效[16]。进一步使用Shapiro Wilk 检验残差的正态性，标准预测值和标准残差的显著性P 值分别为0.314 和0.083，均大于0.05，表明残差近似于正态曲线，满足模型假设。

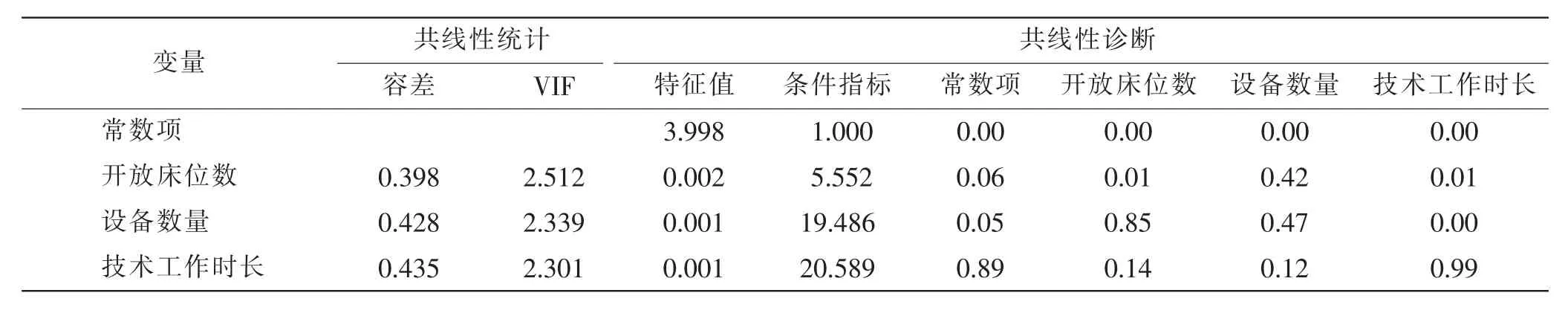
表4 共线性统计及共线性诊断结果Tab.4 Results of collinearity statistics and collinearity diagnosis

3 讨论

笔者研究旨在探讨临床工程人员配置方案，为此在52 家医疗机构的调研结果上建立了预测精度（R2=0.837）很高的多元回归方程模型，这使得医疗机构管理者能够评估需要多少名临床工程人员来执行临床工程部门的主要任务。

进一步分析表3，影响临床工程人员配置数量最重要的因素是技术工作时长。虽然技术工作时长易被工作人员操纵， 但可以通过绩效考核等方法测算[17]，那么技术工作时长就可作为预测临床工程部门人员数量的有效指标[18，19]。 随着临床环境正在从独立的医疗设备向整合的临床系统转变，促进了临床工程部门和信息技术部门之间的任务汇聚，扩展了临床工程人员的工作范围，例如执行信息技术项目，这会导致技术工作时长的增加， 从而需要更多的临床工程人员。而且随着医疗技术的发展， 医疗机构建立了许多分院，形成了临床工程人员网络，这意味着人力资源的共享。临床工程人员往返各分院及总院区之间需花费大量的差旅时间，这进一步解释了临床工程人员数量随着技术工作时长增加而增加的原因。 需要注意的是，为了准确真实测算出临床工程人员的技术工作时长，需要借助信息系统的帮助，首先明确界定临床工程人员的职责范围，其次对各临床工程任务如故障维修、预防性维护、安装验收等进行数据采集，从而测算出临床工程人员的技术工作时长。

既往研究表明开放床位数影响临床工程人员的配备水平[1，20]。 笔者研究结果恰如预期临床工程人员数量随着开放床位数的增加而增加，支持了开放床位数作为临床工程人员配置数量的影响因素。然而需要注意的是，有些医疗机构将长期护理和急诊护理病床混合在一起，而且病例组合指数较高。 重症监护病房内开放的床位数比普通病房内开放的床位数需要配备更多的医疗设备，这就需要配置更多的临床工程人员来进行维护管理。 因此，有必要在后续研究中进一步细化床位数量类型，探讨其对临床工程人员配置数量的影响。

临床工程人员配置数量也随着设备总数量的增加而增加，这一结果支持了David Y 等[8]的研究，因此笔者研究进一步证实了设备总数量是影响临床工程人员数量的重要指标。随着医疗机构配置的医疗设备数量的增加，与技术管理职能相关的工作量也随之增加，那么临床工程部门需要更多的工程人员。 但应考虑到技术管理职能不仅包括医疗设备维护等任务，还应包括其他耗时的任务，比如与医疗器械相关的促进患者安全的任务，而这也是医疗机构的最终目标。

医疗机构的出院病人数未被纳入模型中，因其对多元回归模型产生共线性问题。出院病人数与设备数量之间呈现显著正相关，但一般而言即使减少出院病人数，现有的设备配置仍会保留，因此对临床工程人员的需求保持不变[6，21]。

服务率计算为医疗设备维护总费用/总购置费用[11，12]，以百分比表示，其也未被纳入到多元回归模型中，因为它与人员配置数量不相关。 虽然这一说法仍存在争议[13]，但争议的主要原因是部分被调研医院的信息化程度不高， 以及设备的购置总成本不一致——部分医疗机构记录的是实际支付的价格，而部分医疗机构记录的是合同标价。 此外，零配件成本及是否包含额外维护协议也会影响服务率[22]，因此笔者的结果是不采用服务率作为估算临床工程人员配置水平的测算模型。 随着医疗设备信息化的不断提高，完善的设备操作说明可以帮助临床工程部门确定维持医疗设备平稳有序运行所需的临床工程人员，服务率也会逐渐得到客观数据的支持，未来将被纳入人员配置数量的预测模型中。

临床工程部门所采用的工作模式会影响其工作绩效，更多的任务由内部临床工程人员完成可以帮助医疗机构降低医疗设备维护的总成本。由于目前大多数临床工程部门都使用内部的临床工程人员，无法确定与基于内部模式相比，采用外包模式的临床工程人员数量是否发生变化。因此未来的研究将在分析中加入人员配置模式（内部服务比率及内部服务费用等变量）。

医院复杂性（如是否为教学医院）对临床工程人员配置数量的影响比出院病人数的影响更为直接[8，18]。教学性质的医疗机构拥有的医疗设备比临床治疗诊断型医院需要更多医疗设备，因为它们需要这些医疗设备来教学和培训临床医护人员。由于缺乏有经验的使用人员（实习生、规培生），这些医疗设备可能会产生更多的故障，因此医疗机构需要配备更多的临床工程人员。 因此，教学医院可作为医疗机构出院病人数和临床工程人员数量的调节变量。未来该变量将在调查问卷中体现，确定该变量对临床工程人员数量配置的影响。 此外，为进一步提高模型对医疗机构临床工程人员配置数量的预测能力， 可以纳入更多要素，比如医院的等级及临床工程部门的绩效等。

4 结论

采用笔者提出的多元回归模型对医疗机构临床工程人员配置数量进行预测，相关部门可依此制定相应的临床工程人员配置指标来编制规范要求，作为医疗机构医疗设备安全使用管理规范的保障措施。需要注意的是，该多元回归分析模型反映了医疗机构及其临床工程人员的现状，可能不是最优的，而是局部最优的。例如可能大多数为这种分析提供数据的临床工程部门以一种次优的方式执行临床工程任务，因此使用回归分析作为计划工具只是延续了这种情况，而不是不断地持续改进。 另外，医疗机构临床工程人员的配置水平与医疗机构所在地区的经济发展水平也有一定相关性，笔者研究的调查对象来自特定区域内的某些三级医院，调查对象具有一定的局限性，未来的研究将会在其他地区的医疗机构进行类似的分析，以获得适用面更广泛的预测模型。

（利益冲突：所有作者均声明不存在利益冲突）