一种智能膝关节假肢模型的阻尼参数优化方法

张意彬，吕 杰，喻洪流

根据2006年第二次全国残疾人抽样调查显示，中国各类的残疾人群总数约8 296 万，其中肢体残疾人2 412 万人，占比29.07%，截肢者约186 万人，下肢截肢者占比达85%。 到目前为止，仅有44 万人能够安装下肢假肢[1]。由于经济原因，绝大部分患者仅能穿戴传统机械型假肢（passive prosthesis），只有少数患者能够穿戴智能型假肢（active prosthesis）。 无论是机械型假肢，还是智能型假肢都是由阻尼系统来控制行走支撑相与摆动相的膝关节角度。健康人在行走过程中， 可以利用肌肉的控制完成支撑相和摆动相股骨、胫骨平台的相对转动[2]。与此类似，接受腔所连接的膝关节假肢可以在大腿残肢的带动下完成膝关节的屈曲，在臀部伸肌与阻尼系统的相互配合下，完成健康人的行走步态。臀部伸肌可以部分代偿缺失的膝关节伸肌作用，阻尼系统则可以起到膝关节伸肌和屈肌的调节作用[3，4]。

目前多种膝关节阻尼模型已广泛应用到步态分析中，包括步态模型的建立及不同步速下的膝关节角度预测等，其中大部分研究的重点是利用阻尼系统控制膝关节的运动[5~10]。 阻尼控制系统可分为机械性阻尼控制系统和微处理器阻尼控制系统。机械性阻尼控制系统是利用阻尼调整旋钮的转动来调节阻尼参数，而微处理器阻尼控制系统则是利用内置的软件对阻尼参数进行调节，通过调整阻尼参数，控制阻尼器的能量消耗以维持膝关节在整个步态周期中的屈曲。在步态的支撑相，通过增大阻尼可以提高膝关节的稳定性；在摆动期，通过减小阻尼使膝关节的屈曲变得更加容易[11]。 由此可见，通过适当的调节阻尼参数可以提高膝关节假肢的功能性，让穿戴者得到近乎于健康人的步态， 使其在行走过程中具有更好步态对称性。以往利用人工方法寻找合适的阻尼控制参数不仅效率低，而且准确率也不高，易发生错误。 因此，建构一种有效的膝关节假肢模型来自动寻找合适的阻尼控制参数就显得更为重要。

1 材料与方法

1.1 实验材料

1.1.1 智能膝关节假肢样机

智能膝关节假肢（AiKneeOne）是由上海理工大学康复工程与技术研究所的课题组自行研制的智能型膝关节假肢样机（图1），该样机主要由膝关节假肢与阻尼控制单元两部分组成，通过多组惯性传感器及足底压力传感器获取假肢的运动状态，可对多种行走模式（平路行走、上下坡、上下楼梯等）进行智能识别，并利用微粒群优化的反向传输算法实现了膝关节假肢在平路行走中的摆动相步速跟随控制，详细可参考近期已发表的相关文献[12]。

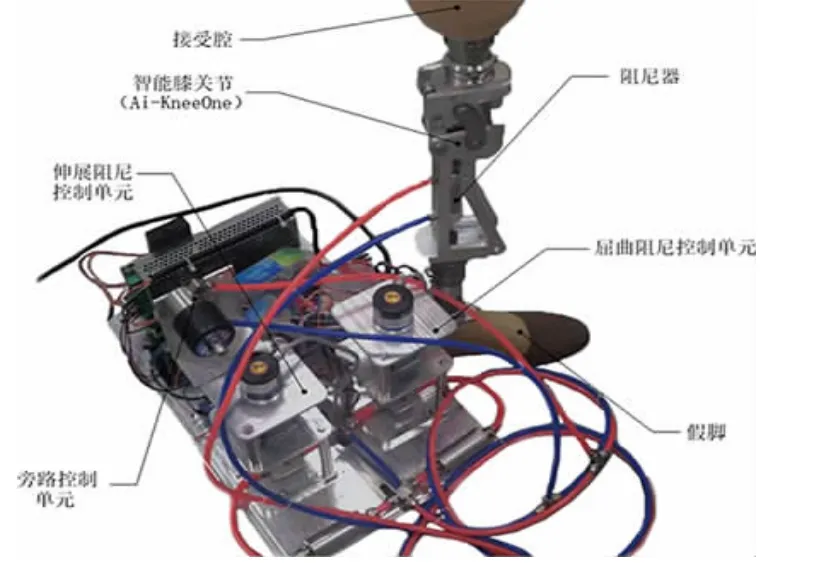
图1 智能膝关节假肢样机（AiKneeOne）Fig. 1 Diagram of intelligent above-knee prosthesis prototype(AiKneeOne)

1.1.2 临床材料

选择测试对象5 例（表1），其中男性3 例，女性2例；年龄29~55 岁，平均年龄44.20 岁（标准差10.45岁）；身高1.52 ~ 1.78 m，平均身高1.650 m（标准差0.098 m）；体质量55~75 kg，平均体质量63.60 kg（标准差8.59 kg）；大腿长0.37~0.44 m，平均大腿长0.404 m（标准差0.027 m）；小腿长0.43~0.51 m，平均小腿长0.470 m（标准差0.029 m）；步幅0.56~0.66 m，平均步幅0.610 m（标准差0.038 m）。且所有测试对象在实验开始前均了解了实验的具体内容，并同意参加实验。

1.2 方法

1.2.1 智能膝关节假肢（AiKneeOne）的模型建构

人体下肢的肌肉、骨骼及韧带等组织在大脑的协调控制下，完成了基本的运动功能，包括站立、坐下、行走、跑步和上下楼梯等基本动作。 骨骼作为中心支架，通过关节连接在一起，肌肉附着于骨头表面，作为动力源，三者共同组成了一个动力系统。 对于下肢而言，髋关节、膝关节及踝关节共同组成了一个多杆刚性系统，下肢可以简化成如图2（a）所示的多连杆的刚性系统（假肢模型model），阻尼单元（阻尼器）既可以作为动力源，在运动过程中提供能量输出，也可以作为能量缓冲器，提供阻尼力，减少和吸收振动，稳定膝关节，其作用相当于肌肉和韧带的功能。 连杆相当于骨骼，连杆之间以铰链形式进行连接，相当于关节。该刚性连杆系统属于平面机构，而人体的骨骼属于空间连杆系统，这里采用简化模型，因为行走步态分析更多的是关注其在矢状面的运动，忽略冠状面和横断面的运动。

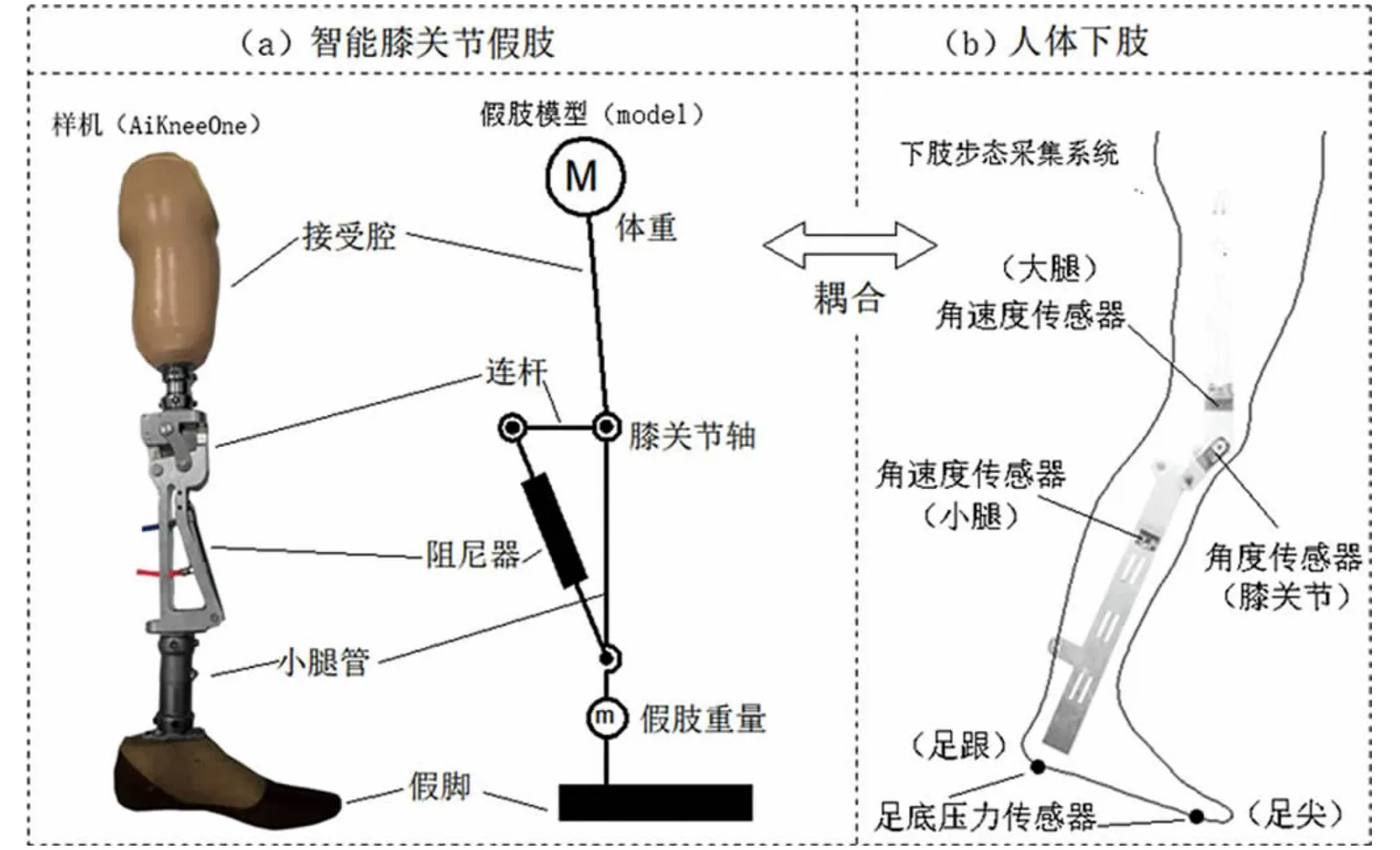
图2 膝关节假肢的耦合建模Fig.2 Diagram of above-knee prosthesis coupled modelling

图2（b）为下肢步态采集装置，大腿段、小腿段所安装的角速度传感器可分别获取大腿、小腿的摆动角速度及角度信息，安装于膝关节的角度传感器可以获取膝关节屈曲、伸展角度信息，足底薄膜压力传感器可以获取足尖处及足跟处的足底压力信息，目前该装置已取得国家发明专利授权[13]。

根据人体行走的步态分析可知，整个行走周期可划分为支撑相与摆动相。 在支撑相，膝关节主要提供扭矩，以保持膝关节在承重时的稳定性，而在摆动相，膝关节更易于屈曲，利用小腿的摆出，为下一次迈步做好准备。 由于两个步态相位的受力状态不同，因此需要对支撑相与摆动相分别建模。 对于支撑相，采用倒立摆模型进行分析（图3a）；而对于摆动相，则直接建立正摆模型（图3b）。 在支撑相，体质量（作用力向下）和足底反力（作用力向上）作用于假肢的阻尼器。在摆动相， 假肢的小腿部分逆重力方向反向转动，没有足底反力的作用，即f=0。

图3 支撑相与摆动相模型Fig.3 Diagrams of stance and swing phase model

图3 中虚线部分是连杆（L2）转动θi角后阻尼器的变化位置。 阻尼器的安装端采用的是曲柄滑块结构，采用该结构方式，可以将阻尼器活塞的直线移动转变成膝关节的转动。 在整个步态周期内，曲柄滑块机构可以根据行走状态提供相应的膝关节转动角度。当连接杆以θi角度发生变化时，则有：

其中：φi代表假肢模型的膝关节角度变化； 其他相关变量及参数详见表2。 表中L1、L2的值取自智能膝关节假肢样机（AiKneeOne）。

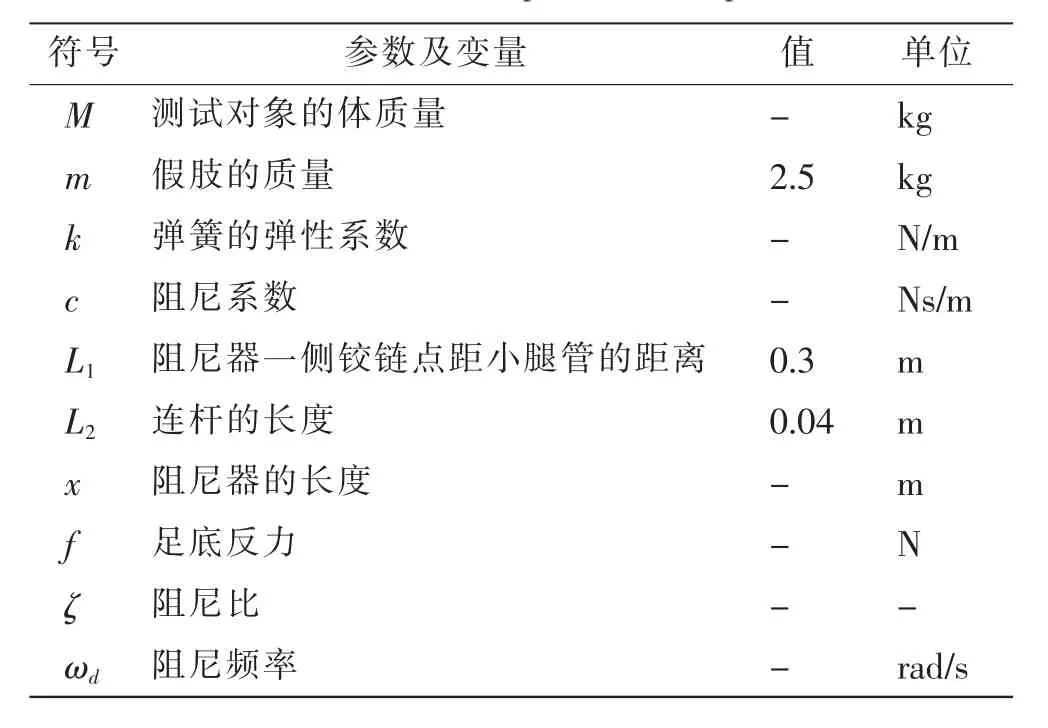
表2 假肢模型的相关变量与参数Tab.2 Related variables and parameters of prosthesis model

1.2.2 阻尼参数预估的优化方法

为了使假肢侧与健肢侧的步态保持一致（步行过程中，双侧下肢的膝关节角度变化相同），在假肢模型（model）中采用Grid Search Optimization 优化法[14]，以假肢模型与真实人体膝关节角度的最小均方根误差为目标，对阻尼参数（ωd，ζ）进行迭代优化：

其中：MMSE 为最小均方误差 （minimum mean square error）；φ 代表假肢模型的膝关节角度；ρ 为真实人体膝关节（knee）的角度。 图4 和图2（b）给出了模型的阻尼参数优化的具体方法。

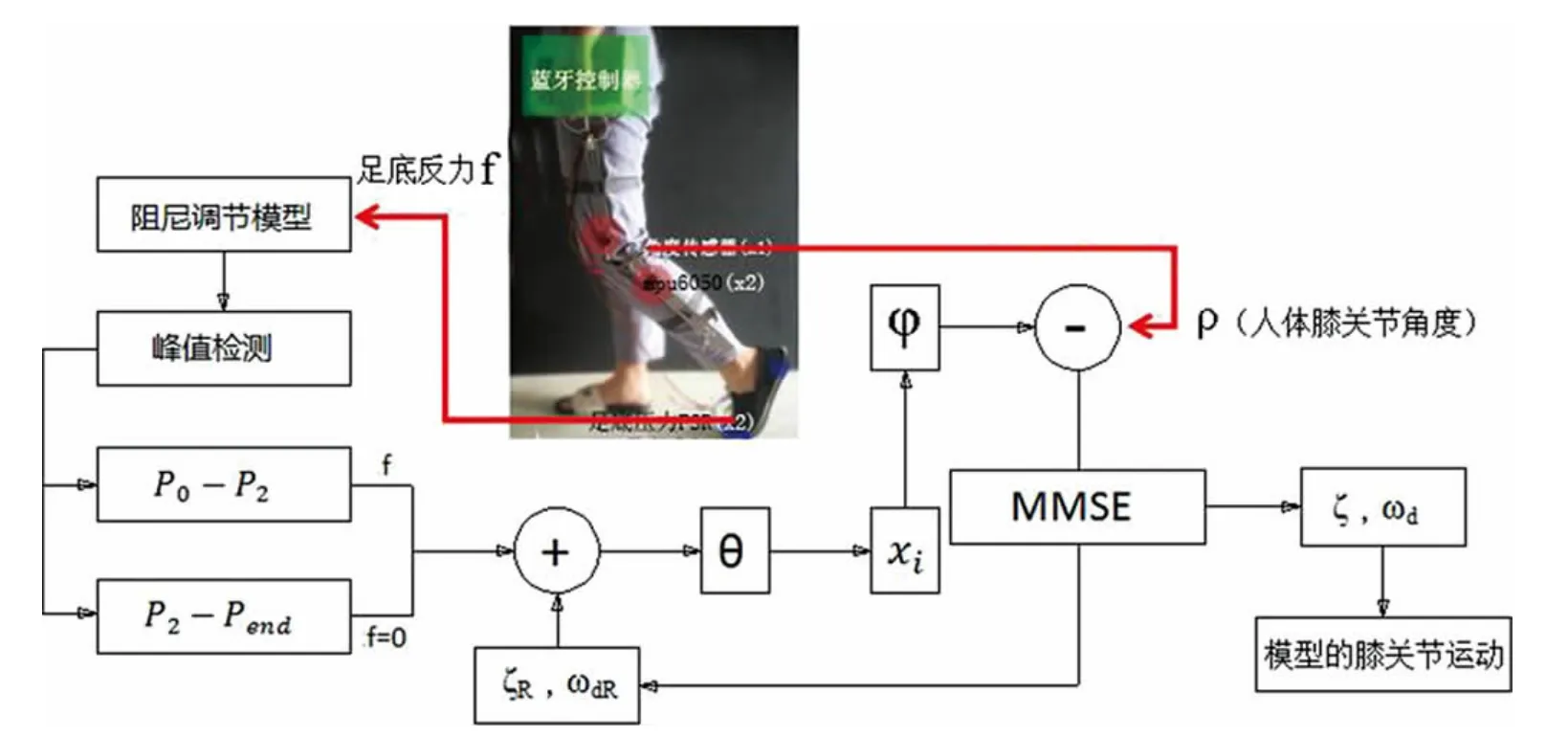
图4 阻尼参数优化方法Fig.4 Diagram of optimization method of damping parameters

图5 中虚线代表足跟处压力传感器获取的压力值， 点线代表足尖处压力传感器测得的压力值，因此叠加两者的测量值，即为整个足底的受力情况（实线）。 利用Matlab 函数库中峰值检测（Peakdet.M），Threshold=50，可以来查找波峰和波谷，从而确定P1与P2点。足底反力的起始点用P0表示，即足跟触地。第一、二次出现的足底反力波峰点分别用P1和P2表示，即足跟最大受力点和足尖最大受力点。 Pend代表摆动相结束。 步态采集频率为100 Hz，即Δt=0.01。在P0-P2（支撑相）之间，定义等时间间隔Δtj（tj-tj-1)内的足底反力增量为Δfj， 增量为正值表示足底压力增加，增量负值表示足底压力减小。 例如，Δf1、Δf2均为正值， 表示t0到t1时刻、t1到t2时刻的足底压力均是增加的；而Δf8为负，表示t7到t8时刻，足底压力减小。

图5 足底反力GRF 的变化曲线Fig.5 Curve of GRF(plantar reaction force)

根据S.S.Rao Mechanical Vibration 的二阶振动理论[15]，即傅里叶级数展开型的阻尼运动，其支撑相（P0- P2），L1与L2之间的角度θ 的变化由如下step函数表示：

其中：i 为采样点；j 为总采样间隔，即i = 1，2，…，j - 1，Δfi=Δfi-Δfi-1；k′弹簧的净弹性系数， 其关系式为：

其中：L 代表膝关节轴至作用于大腿的人体重心距离[16]；k 为弹簧的弹性系数，可表示为：

在摆动相（P2至Pend），L1与L2之间的角度θ 的变化由如下step 函数表示：

其中：A 为P2（摆动初期）时的足底压力最大值；M 为测试者的体质量；ε 为步态相位差别常数，这里ε=0（支撑相与摆动相分别仿真）。

1.2.3 实验测试

测试对象被要求分别以0.8 m/s、1.2 m/s、1.6 m/s的步速平路行走5 min。 利用图1（b）所示的下肢步态采集系统对行走步态的膝关节角度（ρ） 及足底压力（f） 信息进行实时采集， 其中足底压力f 代入公式（4）、（7），可以分别求出支撑相、摆动相的θ 变化，再利用公式（1）、（2）进一步求得φ。根据公式（3）提出的优化函数，结合图4 给出的优化方法，对阻尼参数进行迭代优化。

2 结果

2.1 假肢模型的膝关节角度仿真结果

在P0~ P2区间，需将Δfi、ζ、ωd代入公式（4）对支撑相的膝关节角度（θstance）进行仿真。 而在P0~Pend区间，则仅需将ωd代入公式（7）即可对摆动相的膝关节角度（θswing）进行仿真。 图6 给出了经阻尼参数（ζ，ωd）优化仿真后，不同步速的假肢模型（model）与真实人体膝关节的角度变化曲线。

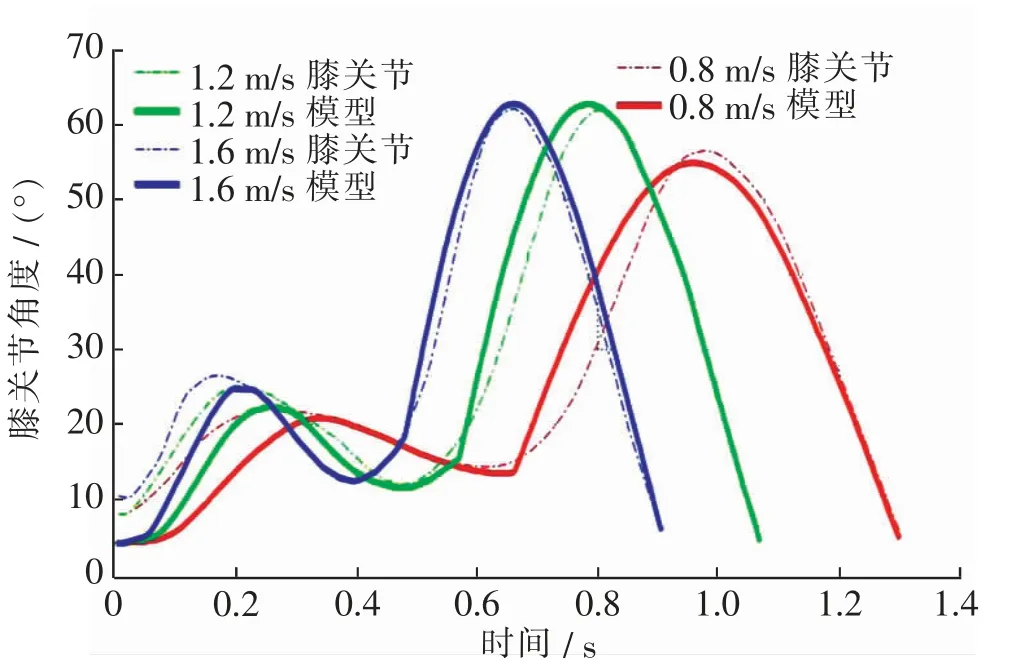
图6 膝关节假肢模型与人体下肢膝关节不同步速的膝关节角度变化比较Fig. 6 Comparison of knee joint angle change curves between knee prosthesis model and human lower limb knee joint at different walking speeds

ζ 和ωd的取值范围分别是：在支撑相，ζR[0，1] =0，0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，1.0；ωdR[1，20] =1，2，3，5，6，7， …，19，20； 在摆动相，ζR[0，0.2]=0，0.001，0.005，0.010，…，0.200；ζR的取值范围取决于考虑阻尼环境下（ζ < 1）的情况，通过减小阻尼器的阻尼力来协助完成摆动相的屈曲态。 鉴于此，在仿真过程中，将阻尼比的范围控制在0~0.2。 ωdR的范围由ωd决定，一个步态周期内，阻尼活塞在支撑期往复1 次，而摆动相则为半次，因此支撑相，摆动相， 其中：T 代表健肢完成一个完整的步态周期所需时间。图6 给出了经阻尼参数（ζ，ωd）优化后的膝关节假肢模型与真实人体下肢膝关节的轨迹曲线对比。

利用均方根误差（root mean squared error，RMSE）及相关系数可以描述真实人体膝关节角度和假肢模型角度之间的相似性，如公式（8）、（9）所示。

其中：Dataknee,i为真实膝关节的角度数据；Datamodel,i经阻尼参数迭代优化的假肢模型角度；n 为总采样点。结果表明：假肢模型与真实膝关节的角度在支撑相的均方根误差为3.8°±0.4°；摆动相相对小些，为1.7°±0.2°。 两者在支撑相的相关性为0.86±0.06，摆动相为0.990±0.005，表现出较好的步态相似性（步态对称性）。

2.2 假肢模型的阻尼参数优化结果

将5 例测试对象的阻尼参数的最终优化值导入Graph pad prism8.4.3，进行数值统计分析（图7、8）。图中可以看出：随着步速的变化，预估参数值的中值也相应发生变化。 支撑相的阻尼频率（ωd）的范围位于5~20，阻尼比ζ 在0.001~0.990；而摆动相的ωd范围则位于3.7~8.6，阻尼比ζ 在0.000 1~0.110 0。 在支撑相，ζ 随着步速的增加而减小， 这是由于阻尼器对增强力的阻力减小造成的， 它与屈曲运动的方向相反。这样有利于维持由于步态增快而导致的支撑相踝关节角度增加。 在摆动相，ζ 值相近，这有利于控制膝关节的胫骨向前运动。 无论是支撑相， 还是摆动相，ωd的值都会随着步速的增加而增加。合适的阻尼参数不仅可以提高支撑相的膝关节稳定，而且还有助于摆动相的假肢小腿前向摆动。

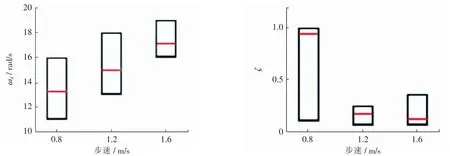
图7 支撑相的阻尼参数（ωd，ζ）优化结果Fig.7 Diagrams of optimized results of damping parameter(ωd，ζ)in stance phase

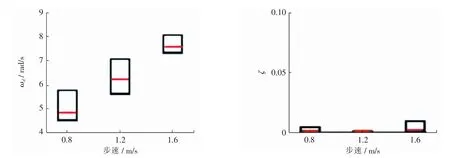
图8 摆动相的阻尼参数（ωd，ζ）优化结果Fig.8 Diagrsms of optimized results of damping parameter(ωd，ζ)in swing phase

3 讨论

笔者研究的目的是寻找一种阻尼参数优化的自动调节方法，提高智能膝关节假肢与健肢侧下肢的步态对称性。利用该方法可以计算出不同步速下的最优阻尼参数预估值。优化的阻尼参数值可以为智能膝关节假肢的穿戴调试提供参考依据，减少大腿截肢者穿戴智能膝关节假肢的适应性训练时间。 另外，没有安装经验的假肢装配师也可以利用此方法快速确定阻尼参数调整参考值。笔者研究中所采用的智能膝关节假肢为研发样机（AiKneeOne），但该假肢模型的应用范围并不局限于此，对于部分结构类似的智能膝关节假肢也可以使用， 只要调整L1、L2、L 等参数的值即可。目前，实验所采集的数据均取自健康人，后续会考虑采集大腿截肢患者的数据。