木-钢组合箱梁抗弯性能试验及有限元对比分析

刘佳桐，雷 云，2，郦 维，陈 领，刘瑞越，王解军

（1.中南林业科技大学 土木工程学院，湖南 长沙 410004；2.广安市广安区交通运输局，四川 广安 638000；3.湖南大学设计研究院有限公司，湖南 长沙 410082）

随着全球经济不断发展，节能、环保、可持续发展理念的不断深入，木结构逐渐发展起来。木材作为一种节能环保的绿色建材，具有轻质高强、保温性能好且美观等优点，但纯木结构受制于木材顺横纹力学性能差异大、抗剪强度低等特点，在高层建筑及大跨度桥梁工程的应用中受到限制[1-3]。钢材具有可塑性好，易加工且污染较小等优点，但钢结构容易发生失稳破坏。将木材和钢材合理地组合成木-钢组合构件能够充分发挥2种材料的优点，克服木材抗剪强度低和钢材稳定性差的缺陷，提升结构的承载能力。

近些年来，对于木-钢组合构件的研究取得了不少成果。陈爱国等[4]将H 形钢和木板进行胶接形成木-钢组合梁，通过试验研究木板及工字钢截面尺寸的变化对组合梁抗弯性能的影响。Wang 等[5]对木-钢组合工字梁和胶合木工字梁的抗弯性能进行了对比试验研究，结果表明组合梁的承载能力远高于胶合木梁。Liu 等[6]设计了3 组等截面高度的木-钢组合工字梁，通过模型试验探究了木板厚度与工字刚度之比参数变化对木-钢组合工字梁弯曲性能的影响。Hassanieh 等[7]研究了不同类型连接件连接的木-钢组合节点荷载-滑移行为和失效模式以及不同类型和间距的剪切连接件（螺栓、自攻螺钉和胶水）、跨度和LVL（Laminated veneer lumber，单板层积木材）板纹理方向（平行和垂直于纹理）对木-钢组合（Steel-timber composite，STC）梁结构性能的影响。Hassanieh 等[8]提出了一种木-钢（交叉层积木材Cross-laminated timber，CLT）组合梁，通过试验及数值模拟分析了不同剪力连接件（四角螺钉、多角螺钉和高强螺栓）进行组合的组合梁的复合效率。张也等[9]研究了集中荷载作用下螺栓间距、剪跨比对H 型木-钢组合工字梁破坏模式、刚度和承载力的影响。Wang 等[10]提出了一种带斜螺钉的木-钢复合材料节点并进行了双剪切面推出试验，研究倾斜角度、专用攻丝机垫圈、螺钉光滑柄长度对钢木组合节点抗剪性能的影响。

综上，国内外学者在木-钢组合工字梁的力学性能及木-钢组合构件连接性能等方面展开了研究，尚未对于木-钢组合箱梁的抗弯性能进行研究。因此，本研究以一种焊接槽钢为骨架，木板作为上、下翼板并通过螺栓连接的木-钢组合箱梁作为对象，通过试验及数值模拟研究组合箱梁的抗弯性能，探明其破坏形态与机理，验证组合箱梁形式的合理性，为木-钢组合箱梁的后续研究提供合理依据。

1 材料与方法

1.1 试件设计

试验共设计1 根纯木箱梁（L0）与3 根木-钢组合箱梁（L1～L3）。纯木梁和组合梁的跨径均为1.8 m，计算跨径均为1.52 m，木箱梁在加载点和支座处胶接了20 mm 厚的木横隔板，组合箱梁在加载点和支座处焊接了3 mm 厚的钢横隔板。组合箱梁的上、下翼板均是由松木锯材加工而成的木板，腹板是由 Q235 钢材加工制作而成的槽钢，由螺栓进行连接。木箱梁由木板胶合而成，试件的设计如图1 所示，其中：ts、bs分别为槽钢的厚度、腿宽，槽钢腿厚与腰厚相同；b1、b2分别为上、下翼缘板宽度；t为木板厚度；bs1、bs2分别为腹板内侧至上、下翼板外侧的距离；bw为腹板内侧之间的距离，槽钢竖立放置，腿端部与下翼板侧边平齐；木箱梁中腹板翼缘木板等厚；hw为箱梁腹板高度；h为箱梁的总高度。

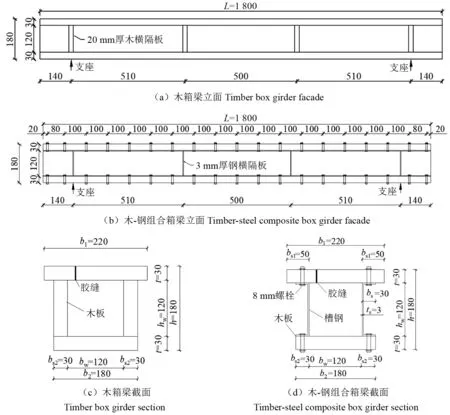
图1 试件设计Fig.1 Design diagram of specimens

1.2 材料属性

1）木板

木材采用兴安落叶松，按照我国木结构试验方法标准[11]中规定的方法加工制作清材小试件进行材性试验，并根据《木结构设计手册》[12]和《木结构设计原理》[13]对试验结果进行折减，其力学性能指标结果如表1 所示。

表1 木材力学性能指标Table 1 Timber mechanical property indexes MPa

2）钢材

槽钢采用Q235 钢材焊接加工而成，钢材的力学性能数据见表2。螺栓采用4.8 级的六角头M8螺栓，螺栓的布置满足我国钢结构设计标准GB 50017—2017[14]和欧洲EN 14545 标准[15]中的要求。

表2 钢材力学性能指标Table 2 Steel mechanical property indexes MPa

1.3 试验方法

试验在中南林业科技大学结构实验室的100 t 级反力架下进行，并用30 t 级荷载传感器进行荷载的测量，采用三等分点分级弯曲加载的方式，加载装置的布置照片见图2a—b。当荷载小于80 kN 时，每级的荷载增量为10 kN；当荷载大于80 kN 时但小于120 kN 时，每级荷载增量为5 kN；当荷载超过120 kN 时，每级荷载增量为2 kN，直至构件不能继续承载为止。

图2 加载装置及应变布置Fig.2 Loading device and strain arrangement diagram

试件加载过程中应变片及位移传感器的读数均由DH3861 静态应变采集系统进行同步采集。测点布置方案为：在每个试件跨中位置的底面布置2 个位移传感器（取平均值）以测量跨中截面的竖向挠度，在组合梁的梁端木材与钢材交界面处布置一个位移传感器用于测量木-钢界面相对滑移，即在加载过程中由于剪力连接件逐步失效而导致木材与钢材产生的相对错位；在每个构件跨中截面的顶面和底面均匀布置5 个应变片，组合梁上翼板的底面布置1 个应变片；组合梁侧面腹板部分均匀布置3 个应变片，侧面上翼板布置1 个，下翼板布置2 个，木箱梁侧面布置6 个应变片，两侧对称布置，测点布置见图2b—d。本次试验主要测量各试件的跨中挠度和跨中截面的应变、极限荷载及木-钢交界面的相对滑移。

1.4 有限元方法

为了更好地研究木-钢组合箱梁的抗弯性能，本研究基于ABAQUS 软件建立了木箱梁和组合箱梁的有限元模型，并将数值模拟结果与试验结果进行对比，验证有限元模型的合理性。

1.4.1 有限元模型的建立

木箱梁和组合箱梁在ABAQUS 软件中均采用3D 建模的方式，采用八结点线性六面体单元（C3D8R）的方式对木板、钢型材和支座进行建模并划分网格。木板以10 mm 的网格进行布种并划分；钢腹板划分为6 mm 的网格；由于支座垫板会对试验结果不产生影响，故将其划分为20 mm的网格。最终木箱梁和组合箱梁的网格划分有限元模型如图3 所示。木箱梁和组合箱梁的支座一边简化为铰支座，一边简化为链杆连接。采用集中力的方式对模型进行加载。

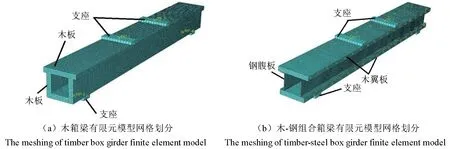
图3 试件有限元模型Fig.3 Finite element model of the specimen

1.4.2 材料和剪力连接件本构关系

在3D 有限元模型中，钢屈服和塑性行为由弹性各向同性硬化塑性本构定律模拟，其弹性模量为206 Gpa，质量密度为7.85 g/cm3，泊松比为0.3，当考虑塑性变形时，真实的应力应变数据应进行输入，其满足如下关系：

真实塑性应变为材料的真实应变减去弹性阶段的应变，即：

式中：ε、σ和εy分别表示材料的真实应变、真实应力和真实塑性应变；ε1、σ1分别表示名义应变和名义应力；E为材料的弹性模量。

木材为正交各向异性材料，木材在拉压应力状态下弹塑性行为分别由工程常数和Hill 屈服准则来实现。木板的物理力学参数如表3 所示。表4给出了木材塑性屈服强度比Rij，由下式定义：

表3 木材物理力学指标Table 3 Timber physical and mechanical indicators

表4 木材屈服强度比Table 4 Timber yield strain ratios

式中：σy为材料塑性参考屈服正应力；τy为参考屈服剪应力，σii和σij为屈服正应力和屈服剪应力。

螺栓采用弹簧单元进行模拟，将翼板内表面与钢腹板对应的两点进行连接，并释放梁纵向自由度，以连接刚度进行模拟。连接刚度满足欧洲木结构规范[16]，由下式进行计算：

式中：u为弹簧的连接刚度；γ为木材的气干密度；d为螺栓连接件的直径。

2 结果与分析

2.1 破坏现象、形态及机理分析

各试件的破坏形态如图4 所示。加载初期，木箱梁并无任何明显的破坏现象，随着荷载增加至极限荷载的80%时，木箱梁开始发出清脆的木纤维撕裂声，在加载点的下方，腹板中部出现细微的纵向裂缝；随着荷载继续增大，纵向裂缝迅速向梁端延伸，同时不断发出撕裂的响声，随着一声巨响，纵向裂缝延伸到了梁端，木箱梁破坏。3 根组合箱梁在加载初期并无明显的破坏现象，当荷载达到极限荷载的60%左右时，组合梁的木板开始发出响声；当荷载超过极限荷载的80%时，组合箱梁不断发出沙沙的木材撕裂声，木翼板出现了较大的局部裂缝，梁的弯曲程度迅速增加；到达极限荷载时，3 根组合箱梁上翼缘钢材均局部受压屈服，底板的木材均拉裂断开而破坏。

图4 试件的破坏形态Fig.4 Failure patterns of the specimen

2.1.1 木箱梁破坏模式与机理分析

木箱梁为腹板中部木材产生剪切裂缝的脆性破坏模式（图4a）。由于木材具有较高的顺纹抗拉和抗压强度，剪切强度较低，木翼板的拉压应力还未达到木材的抗拉压强度，腹板中部的剪切应力就已超过木材的顺纹抗剪强度，随即发生剪切破坏，并形成一条通长的剪切裂缝，因此木箱梁丧失承载能力而被破坏。在木箱梁上翼板顶面出现了纵向的局部裂缝（图4b），这是由于木材存在木节、斜纹等缺陷，在木节处会产生应力集中，从而导致在木节等缺陷处出现局部裂缝并逐渐延伸，最终发生脆性剪切破坏。

2.1.2 组合箱梁破坏模式与机理分析

组合箱梁为典型的下翼缘木板受拉断裂的破坏模式。在破坏时，底板木材的拉应力已超过木板的极限抗拉强度，因此底部木板纤维被拉断而破坏（图4d、g、j）；在接近极限荷载时，上翼缘加载点附近的螺栓处出现木板局部劈裂现象（图4e、h、k），这是由于螺栓受到木板的挤压而使木板产生了较大的横纹拉应力，并伴随着剪力滞效应；钢腹板上翼缘出现局部屈曲的现象（图4f、i、l），这是由于槽钢翼板较短，在加载点处钢腹板上翼缘受到了较大的压应力。

2.2 荷载-跨中挠度曲线

木箱梁和组合箱梁的荷载-跨中挠度曲线如图5 所示。随着荷载的增加，木箱梁的荷载-挠度曲线基本保持线性增长，这表明木箱梁始终处于弹性变形阶段；木-钢组合箱梁则表现出了理想的弹塑性行为，加载初期，荷载-挠度曲线呈线性增长，后期挠度的发展速度显著增加，表明相比于木箱梁，木-钢组合箱梁具有更好的延性。本研究基于Yasumura[17]提出的方法将组合箱梁初始刚度k定义为荷载-挠度曲线在极限荷载的0.1 倍与0.4 倍两点之间连线的斜率，即：

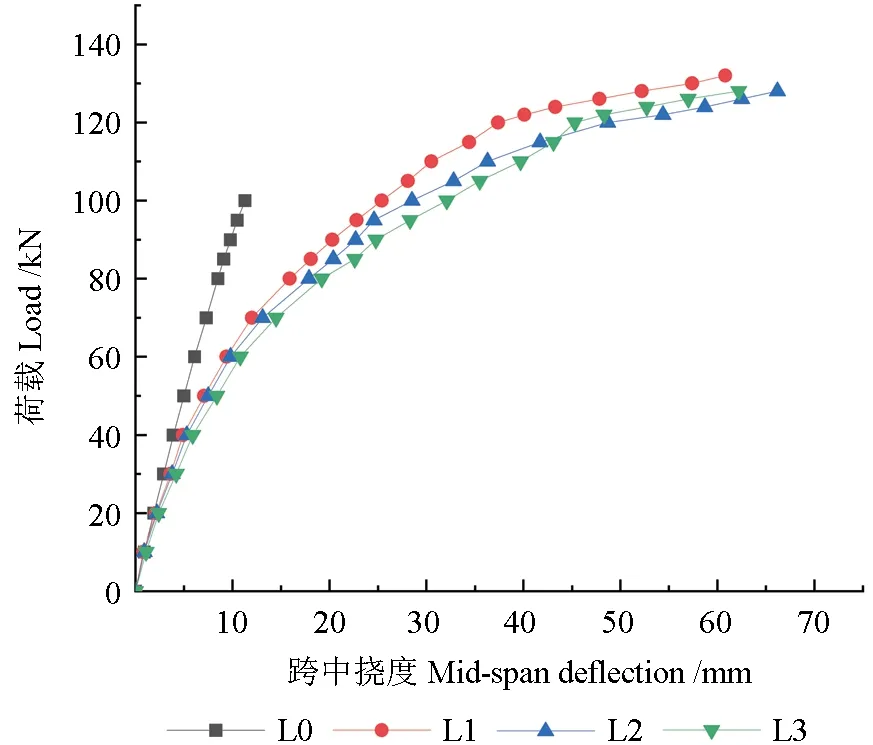
图5 荷载-跨中挠度曲线Fig.5 Load-midspan deflection curves

式中：Pu0.4和Pu0.1分别为0.4 倍极限荷载和0.1 倍极限荷载；Δd为荷载-挠度曲线上0.4 倍极限荷载Pu0.4和0.1 倍极限荷载Pu0.1之间的位移差。

屈服点的定义采用等效弹塑性屈服法。如图6所示，屈服位移取荷载-挠度曲线具有相同初始刚度和极限强度的弹塑性系统的屈服位移，则试件的延性系数和屈服位移Δy的计算式为：

图6 等效弹塑性屈曲Fig.6 Equivalent elasto-plastic buckling

式中：Py、Δy、Pu、Δu和β分别代表试件的屈服荷载、屈服位移、极限荷载、极限位移和延性系数。

木箱梁和组合箱梁的主要力学性能指标如表5所示。相比于木箱梁，木-钢组合箱梁的承载能力得到显著提升，组合箱梁的极限承载力平均提高了30.33%，表明木材和钢材的力学特性得到了充分的发挥。初始刚度平均下降了34.42%，这是由于木箱梁腹板与翼板之间采用胶合的方式进行连接，其整体性较好，组合箱梁由于采用螺栓进行连接，木翼板与钢腹板之间会产生相对滑移，从而导致组合箱梁的初始刚度下降。

表5 试件的力学性能指标†Table 5 Mechanical properties of the specimen indexes

2.3 跨中截面正应变沿高度变化

图7 为木箱梁（图7a）和组合箱梁（图7b—d）跨中截面应变的分布情况，木箱梁在加载过程中截面应变沿高度方向保持线性分布，说明其始终满足平截面假定。组合箱梁由于采用螺栓连接，木板与槽钢交界面处会产生剪切应力，而木板与槽钢之间的接触面积较小，组合梁在加载初期交界面处剪切应力超过了界面摩擦力，交界面处开始产生滑移，因此组合箱梁截面整体不再满足平截面假定，但木板与槽钢各自满足平截面假定。

图7 跨中截面正应变Fig.7 Normal strain in the cross-section

木材受压会经历弹性阶段和塑性阶段[18-19]，受拉表现为脆性破坏，基于上述研究及表1 中的木材材性指标，经计算可得本研究中木板的屈服压应变为2 301 με，极限拉应变为1 701 με。由图7 可以看出，在加载极限荷载时，组合箱梁实测的木材最大压应变均已超过了3 000 με，超过了木板的屈服压应变，此时，上翼缘顶面的木材已失效，中性轴下移。下翼缘木材的最大拉应变均超过了3 500 με，远远超过了木板的极限拉应变，因此组合箱梁底板木材被拉断而失效。钢材在受力过程中会经历明显的流幅阶段，由表2 可知，本研究中的钢材屈服应变为1 140 με，试验测得钢材的最大拉应变分别为 5 492、5 210 和5 598 με，均已超过了钢材的屈服应变，说明组合梁在接近破坏时部分钢材已经进入屈服阶段，因此钢腹板发生了局部屈曲的现象。综上所述，钢材弥补了木材抗剪性能较低的缺陷，发挥了木材抗拉压性能较高的优点，表明本研究提出的木-钢组合箱梁科学合理。

2.4 组合箱梁荷载-端部滑移响应

由于试验中木-钢组合箱梁采用螺栓进行组合连接，螺栓在组合梁受弯过程中会产生变形，组合梁上、下翼板与钢腹板之间产生相对滑移，引起组合梁的刚度降低和抗弯承载力下降。图8 为木-钢组合箱梁端部的滑移示意图，由图8 可知，木-钢组合箱梁为钢腹板上翼缘相对木板内缩，钢腹板下翼缘相对木板外伸的滑移模式，这是由于钢材的弹性模量远高于木材的弹性模量。本研究以钢腹板相对木板内缩为正，外伸为负，得出荷载-端部相对滑移曲线如图9 所示。3 根组合箱梁上、下翼缘的相对滑移均超过了6 mm，上、下翼缘的滑移变化趋势基本保持对称变化。在70%极限荷载之前，相对滑移随荷载的增加基本保持线性变化，且相对滑移较小，基本保持在2.5 mm 以内，这是由于此时螺栓处于传力的弹性阶段；当荷载超过极限荷载的70%后，其滑移量的增长急剧增加，这是由于螺栓进入了传力的弹塑性阶段，剪切变形迅速增大，螺栓的抗剪刚度大幅下降。

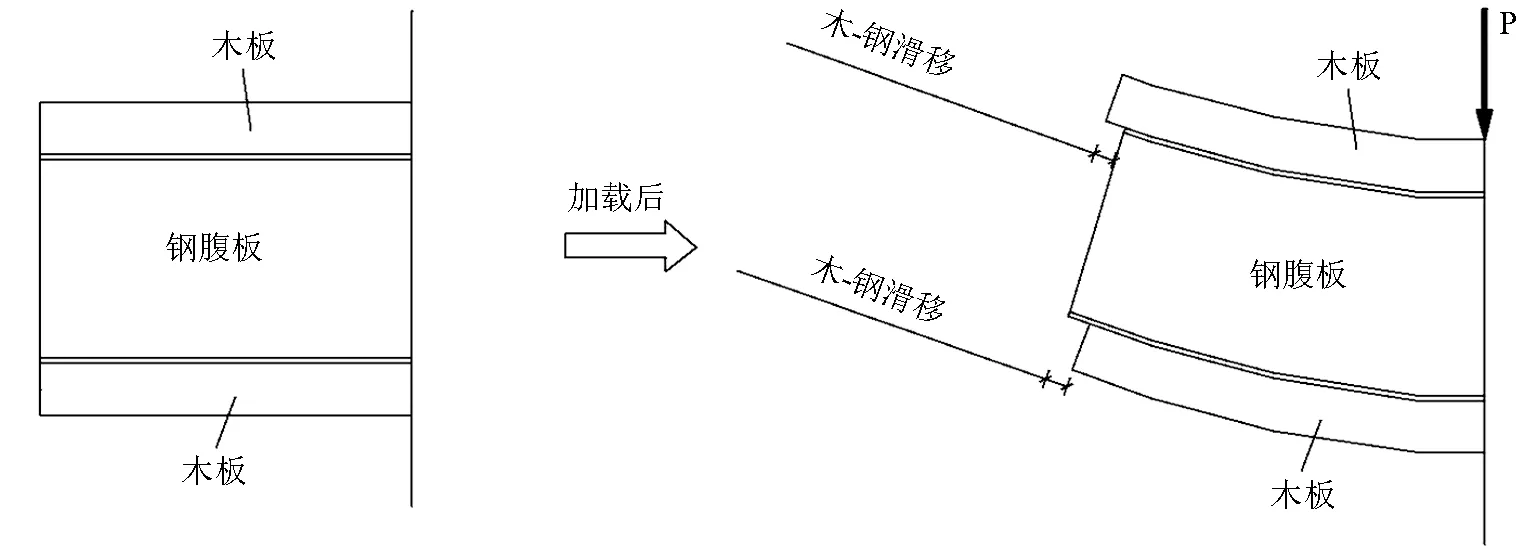
图8 木-钢组合箱梁滑移模式Fig.8 The sliding mode of timber-steel composite box beams

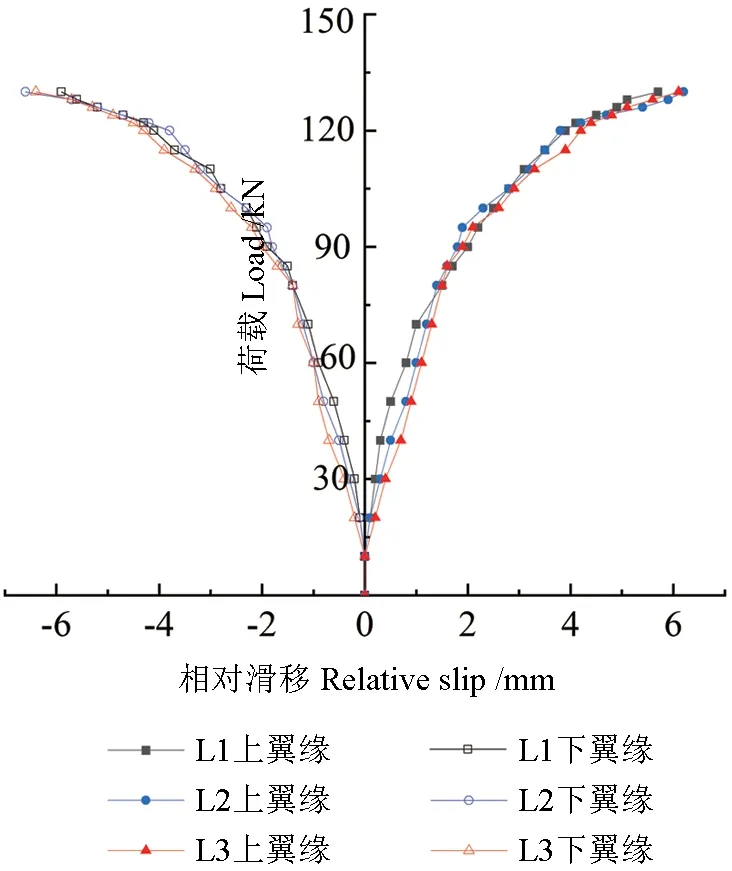
图9 组合梁荷载-端部滑移曲线Fig.9 The load-end-slip curve of composite beams

2.5 上翼缘板正应变的横向分布

箱梁通过肋板传递给翼板的剪应力是不均匀的，在肋板交接处最大，远离肋板开始逐渐减小。因此，本次试验在4 根试件上翼缘板顶面的中部沿横向均匀布置了5 个纵向应变片（图2c—d）用于测量上翼板正应变沿横向的分布情况。图10 显示了上翼板顶面在各级荷载下的应变横向分布情况，由图10 可以看出，加载初期其正应变沿横向基本保持均匀分布；当超过极限荷载的40%时，腹板位置的翼板正应变开始大于远离腹板位置的正应变，随着荷载的增加，正应变沿横向分布不均匀程度逐渐增大，这是由于腹板的剪切应力逐渐增加，剪力滞后效应逐渐增大所致。本研究基于徐果[20]、李平等[21]的研究对各试件有效宽be进行了简化计算，确定了木箱梁和组合箱梁的翼板有效宽度，计算公式如下：

图10 跨中上翼板顶面正应变横向分布Fig.10 Transverse distribution of normal strain on the top surface of mid-span upper flanges

式中：b为各箱梁试件翼板的实际宽度；λ为剪力滞系数；σmax是翼板处的最大正应力；σ0为按初等梁理论求得的翼板截面平均正应力。

表6 给出了木箱梁和各组合箱梁跨中位置上翼板的剪力滞系数和翼板有效宽度，由表6 可知，木箱梁的剪力滞系数小于组合箱梁，这是由于木箱梁的腹板较宽，其肋板的剪切应力传递相对较为均匀，因此受剪力滞后效应的影响相对较小，组合箱梁的腹板较薄的钢材剪力滞后效应更明显，因此木箱梁的翼板有效宽度也大于组合箱梁。

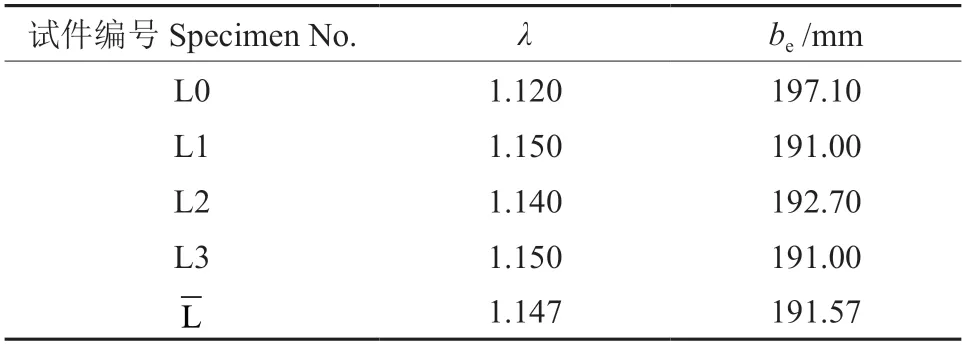
表6 跨中截面上翼板剪力滞系数及有效宽度†Table 6 The shear lag coefficient and effective width of flange plates on the mid-span cross section

2.6 有限元与试验结果对比

有限元模拟结果与试验结果对比分别如图11～12 所示，图11 显示了有限元模拟结果与试验获得的荷载-跨中曲线对比结果。由曲线可以看出，木箱梁和组合箱梁有限元模拟的曲线与试验结果拟合较好，木箱梁的跨中挠度最大值为11.89 mm，这与试验测得的挠度值11.30 mm 较为接近；木-钢组合箱梁的跨中挠度最大值为59.09 mm，与试验中3 根组合箱梁试件实测的跨中挠度位平均值62.70 mm 也非常接近，这说明有限元数值模拟分析的结果与实际情况是比较符合的。图12 显示了有限元模拟的梁跨中上翼缘板正应变的横向分布与试验结果的对比情况（木-钢组合箱梁的试验结果取3 根试件的平均值），有限元模拟的结果应变值略小于试验值且对称性较好，这是由于有限元模拟时忽略了木材木节、开孔等因素。表7 给出了有限元模拟得出的剪力滞系数、上翼板有效宽度与试验值的对比结果，其相对误差基本在5%以内。综上所述，有限元模拟的结果能够很好地反映木箱梁与组合箱梁的弯曲性能。

表7 剪力滞系数和有效分布宽度的试验结果与有限元结果对比†Table 7 The experimental results of shear lag coefficient and effective distribution width with the finite element

图11 跨中挠度曲线试验结果与有限元结果对比Fig.11 Test results of deflection curves in mid-span with the finite element

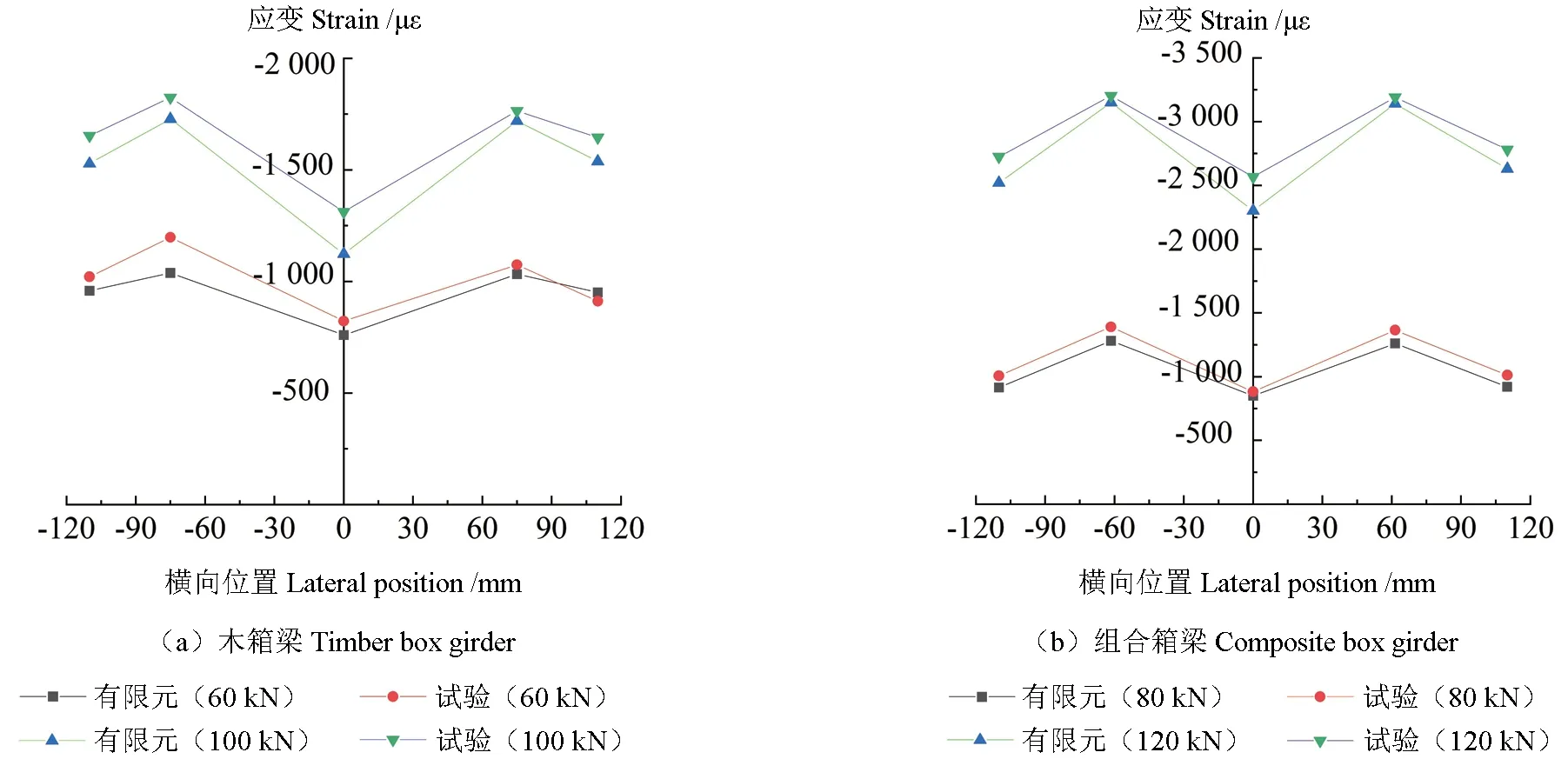
图12 跨中上翼板顶面正应变横向分布试验结果与有限元结果对比Fig.12 Test results and finite element results for normal strain transverse distribution at the top surface of the mid-span upper flange

3 结论与讨论

3.1 结 论

通过对木-钢组合箱梁和胶合木箱梁的弯曲加载试验与分析，得出以下结论：

1）组合箱梁为底板木材受拉断裂的破坏模式，同时伴随着顶板木材受压产生局部劈裂破坏和钢材上缘的屈曲，其为延性破坏；木箱梁为腹板中部产生贯通裂缝的剪切破坏，其为脆性破坏。组合箱梁的腹板采用了强度较高的钢材，克服了木材顺纹抗剪能力较差的缺点，充分发挥了木材拉压强度较高的优点，表明该组合形式是合理的。

2）组合梁的极限抗弯承载力较相木箱梁平均提高了30.33%，且其延性远高于木箱梁；由于组合箱梁采用螺栓连接，其界面会产生滑移，因此导致组合梁的初始刚度低于木箱梁；通过分析翼板应变的横向分布情况发现2 类梁均有明显的剪力滞效应。

3）基于ABAQUS 软件建立的有限元模型的模拟结果较为准确，木箱梁与组合箱梁模拟的挠度值、剪力滞系数及翼板有效分布宽度与试验值吻合较好，误差基本在5%以内，能够很好地用于实际工程的模拟预测。

3.2 讨 论

木-钢组合箱形截面梁是一种新型组合结构，其研究理论体系尚不完善，对于其受力性能的研究还有待深入，在此提出以下讨论：

1）采用螺栓连接的木-钢组合梁其交界面产生滑移，从而影响组合梁的抗弯性能，因此，采用剪力连接件进行结合的木-钢组合箱梁的连接性能需要进一步研究。

2）本研究中并未对木-钢组合箱梁承载能力的影响因素进行研究，比如截面几何特性参数和跨度等，尚需开展承载力影响因素的相关研究。

3）只针对木-钢组合箱梁的抗弯性能进行了研究，抗剪性能在实际过程中亦不可忽略，尚需对其抗剪性能开展研究。