湖南省杉木二元立木材积模型的检验与调整

陈 静，周根苗，易 烜，许冰冰，吕 勇

（1.中南林业科技大学 林学院，湖南 长沙 410004；2.湖南省农林工业勘察设计研究总院，湖南 长沙 410007；3.湖南省青羊湖国有林场，湖南 宁乡 410600；4.福建省林业勘察设计院，福建 福州 350001）

森林蓄积量是指一定森林面积上存在着的林木树干部分的总材积，是反映森林生长情况和森林生态活力的指标，一般可以通过构建立木材积模型编制立木材积表进行森林蓄积量预估。我国常用的立木材积表包括一元材积表和二元材积表[1-3]，分别为基于胸径或树高和胸径的立木材积模型[4-6]。由我国农林部颁布的二元立木材积表[7]至今已有40 多年，与编表时相比，现全国森林资源结构已发生很大的变化，当前的森林资源情况可能不再适用于原颁布的二元立木材积表[6]。

随着统计学与计算机科学的快速发展，考虑到生境复杂性对树木生长的影响，越来越多的学者采用更复杂的模型来预估活立木材积，以期提高模型的精度与适用性。近年来，学者们在生产实践中普遍认为山本材积式适用性好、精度高、应用广[8]。有学者以山本式为基础模型，考虑到胸径和树高的变化率，如黄四南等[9]、陈怡[10]构建的可变参数动态模型提升了原模型精度。此外，哑变量模型和混合效应模型在林业中都有成功的应用[11-13]，如曾伟生等[14]将树种和区域作为随机效应变量、哑变量，构建线性混合模型和哑变量模型比总体平均模型的精度要高；赵浩彦等[15]运用多元非线性混合模型构建南京地区马尾松材积模型，与山本式二元材积模型相较拟合精度更高。陈振雄等[16]考虑分枝数、区域、品系为随机变量，构建海南省橡胶树立木材积混合效应模型，明显优于常规模型。可以看出，基于不同的改进方法的山本式二元材积模型与其常规模型相比较，改进模型的拟合效果更好，精度更高。

杉木Cunninghamialanceolata是我国南方人工造林的重要树种，水平分布在我国整个亚热带、热带北缘等气候区的19 个省（区、市），垂直分布在海拔130～2 900 m 的丘陵山地[17]，较喜光，喜温暖湿润，是湖南省的主要造林树种之一。根据第九次全国森林资源清查显示，按优势树种分，杉木人工林面积和蓄积量位居前10 位，相较于第八次森林资源清查，杉木面积名次有所上升[18]。为精确估算湖南省杉木的材积量，针对现有湖南省杉木二元立木材积模型存在误差的问题，本研究以湖南省杉木为对象采集数据，以山本材积式为基础模型构建可变参数模型；以区域因素为随机变量、哑变量构建哑变量模型和混合效应模型，为找到适用于湖南省杉木的二元立木材积模型提供理论依据。

1 研究区概况

湖南省位于长江中游（24°38＇～30°08＇N，108°47＇～114°15＇E），总面积约21.18×104km2。湖南属亚热带季风气候，大陆性亚热带季风湿润气候带，主要为山地和丘陵，以红壤和黄壤为主。湖南省森林资源丰富，森林覆盖率为59.7%，林业用地面积为129.98×105hm2，约占全省国土总面积的61.4%，活立木总蓄积量5.05 亿m3。境内现有高等植物5 000 多种，其中木本植物1 900 多种，主要树种包括马尾松Pinusmassoniana、杉木、樟树Cinnamomumcamphora、檫树Sassafrastsumu、栲Castanopsisfargesii等[19]。杉木人工林面积占全国人工乔木林总面积的1/4 和总蓄积量的1/3。其中，湖南省杉木人工林面积和蓄积量分别占全省的33%和41%[20]。

2 材料与方法

2.1 数据来源

数据来源于湖南省杉木人工林的调查数据，样地大小约为667 m2，数据采集于湖南省常德、郴州、衡阳、永州、邵阳、湘西州和益阳，共1 002 个样地，采用3 倍标准差法剔除异常数据，剔除异常数据后为973 株杉木标准木，按3∶1 比例选取729 株标准木数据为建模数据，244 株标准木数据作为检验数据，数据分布情况如表1 所示，解析木按径阶与树高级大小的分配情况如图1 和图2 所示。

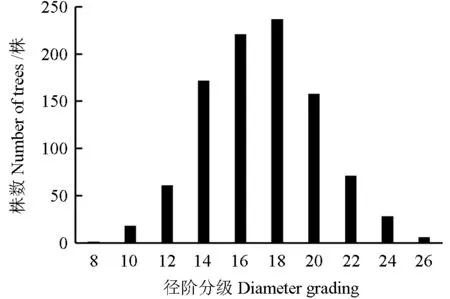
图1 解析木株数按胸径大小的分配情况Fig.1 The distribution of trees by DBH

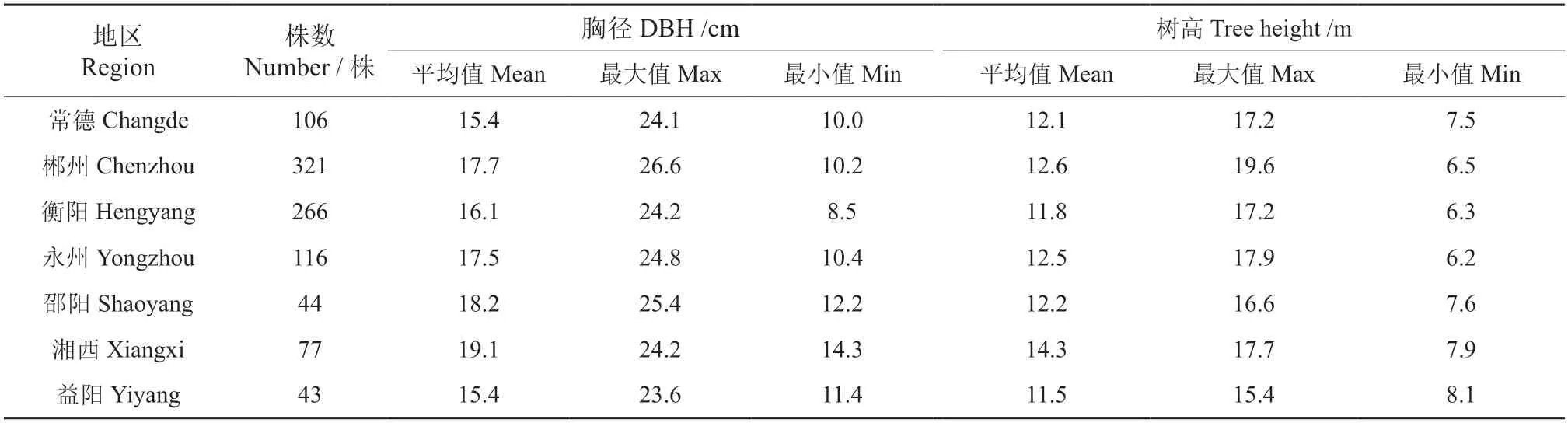
表1 样木基本情况Table 1 Basic information of the sample woods

2.2 标准木材积计算

1）中央断面积区分求积法：

将树干按一定长度（通常1 m 或2 m）分段，量出每段中央直径和最后不足一个区分段梢头底端直径。

当把树干区分为n个分段，利用中央断面近似求积式求算各分段的材积，其总材积为：

式中：gi为第i区分段中央面积；g＇为梢头底端断面积；l为各区分段的长度；l＇为梢头长度；n为区分段个数。

2）现有湖南省杉木立木材积模型[9]

式中：c0、c1、c2为参数，其中c0=0.000 058 777 042，c1=1.969 983 1，c2=0.896 461 57。

2.3 研究方法

2.3.1 配对t 检验法

采用配对t检验来比较原二元立木材积与实际材积的2 组数据是否存在差异性。采用SPSS 23.0软件对2 组数据进行比较。

2.3.2 固定参数模型

对于主干材积而言，山本材积式最适合湖南省杉木材积的计算，能较好地反映干性、胸径和树高对材积的影响，因此，选山本式为基础模型，模型的结构式为[8]：

式中：V为材积，D为胸径，c0、c1、c2为模型参数。

2.3.3 可变参数模型

树干的材积不仅与胸径和树高这2 个变量有关，还与胸径和树高的表现形式有关，也与模型中的参数是否可变有关。因此，为了提高二元立木材积模型的预估精度，将山本式中的参数设计成胸径和树高相关的函数式，得到可变参数模型结构如下[10]：

根据不同胸径级与树高级分别进行拟合分析，将可变参数动态模型设计如下：

式（5）中：V为材积，D为胸径，H为树高，c0、c1、c2、c3、c4为模型参数。

2.3.4 混合效应模型

材积模型的建立可以采用混合模型的方法[14]，利用湖南省7 个地区的实测数据直接建立木材积模型存在一定的偏差，立木材积模型的误差大小可能与地区的气候和温度等因子有关。将区域作为随机效应变量构建混合效应模型。混合效应模型有2 种形式，一是线性混合效应模型（Linear mixed effects model，LME），二是非线性混合效应模型（Nonlinear mixed effects model，NLMES）[12]。

混合效应的表达式如下：

式中；yi为第i个因变量向量；a为固定效应参数向量；δi为随机参数向量；xi为第i个自变量向量。

2.3.5 哑变量模型

材积模型的建立也可以采用哑变量模型的方法[14]。哑变量也称虚拟变量，通常取值为0、1 或-1。将区域因子作为哑变量引入到湖南杉木立木材积再参数化模型中，处理时，将变量赋值来表示定性或分类变量[21]，即：

本研究将区域这个分类变量作为哑变量，郴州地区划分为1 则其他地区划分为0，构建含区域哑变量的杉木立木材积模型。

2.3.6 异方差处理

由于立木材等数据存在异方差，在对模型参数求解时必须消除异方差的影响。通常采用加权回归或者对数回归法消除，本研究采用R 语言，运用非线性回归分析加权最小二乘法拟合二元材积方程。

2.4 模型精度评价

采用SPSS 23.0 等软件对数据进行分析，得到模型参数，本研究采用确定系数（R2）、总相对偏差（TRB）、平均系统偏差（MSB）、均方根误差（RMSE）、赤池信息准则（AIC）及贝叶斯信息准则（BIC）等指标对模型进行检验，计算公式如下：

式中：yi为第i样本实测值，是第i样本预估值，为平均实测值，p为模型中参数的个数，n为样本数，l表示模型极大似然函数值。

3 结果与分析

3.1 配对t 检验

采用SPSS 23.0 软件对湖南省当前使用的二元立木材积模型计算的材积值与中央断面积计算的实测材积值进行配对t检验，具体的检验结果如表2 所示。

表2 配对t 检验结果Table 2 The paired t-test results

由表2 可以看出，P值（即Sig.）小于0.05，所以可以推翻原假设，即现有的湖南杉木材积模型计算值与实际材积计算值存在显著差异。

3.2 湖南省现有杉木二元立木材积模型的调整

3.2.1 固定参数模型与可变参数模型的拟合结果

利用加权回归分析法，以模型的倒数为权函数，使用R 语言的nls 函数对材积方程进行拟合，得到固定参数模型与可变参数模型的拟合结果并对其进行检验，具体结果如表3～4 所示。如表3所示，模型的拟合结果良好，确定系数（R2）都在0.95以上，固定参数模型与可变参数模型的均方根误差（RMSE）无显著差异，总相对偏差（TRB）与平均系统偏差（MSB）均在±3%范围内，可变参数模型的总相对偏差与平均系统偏差趋近于0，相对来说，可变参数模型相较于固定参数模型，拟合效果更好。通过分径阶对模型进一步检验，结果如表4 所示，从整体上看，固定参数模型和可变参数模型的总相对偏差和平均系统偏差都在±3%范围内；在24 cm 径阶固定参数模型的总相对偏差和平均系统偏差高达±7%，而可变参数模型径阶的偏差相对较小，在大径阶和小径阶的效果更为明显，基本都优于固定参数模型。

表3 固定参数模型与可变参数模型拟合结果Table 3 Fitting results of the fixed parameter model and variable parameter model

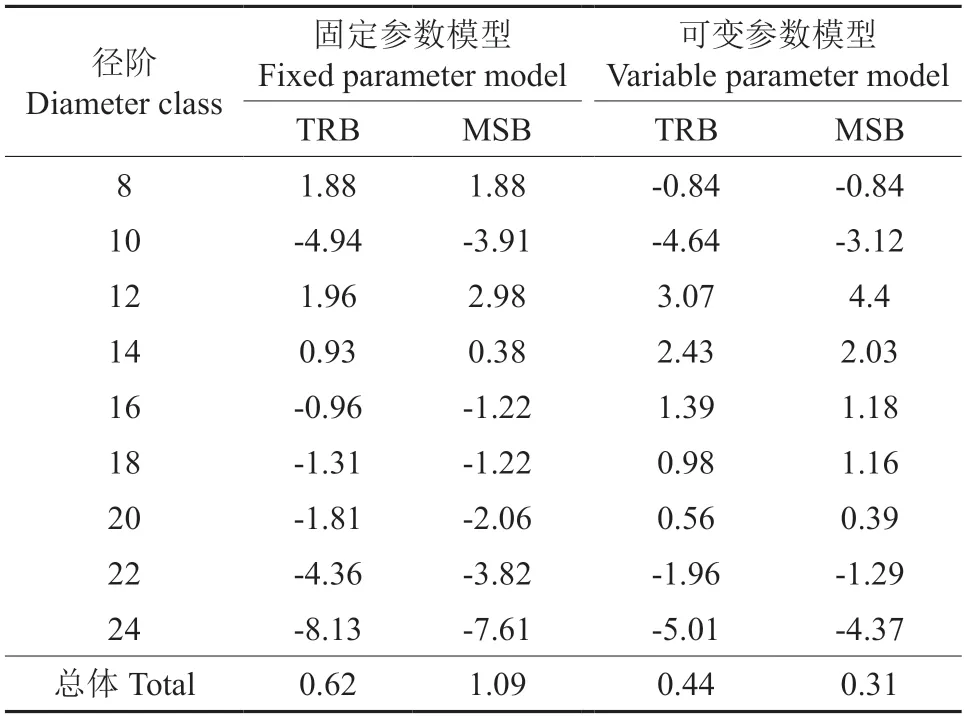
表4 固定参数模型与可变参数模型分径阶检验结果Table 4 Diameter order test results of fixed parameter model and variable parameter model

为了进一步了解固定参数模型与可变参数模型的差异，分别建立了比较图与残差图，如图3～6所示。

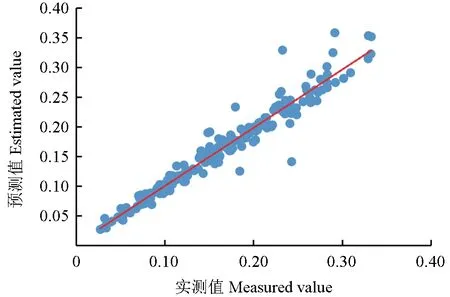
图3 实测值与固定参数模型预测值比较Fig.3 Comparison between the measured value and predicted value of the fixed parameter model

从图3 和图5 可以看出拟合精度较好，可变参数模型的拟合精度比固定参数模型更优，从图4和图6 可以看出残差值较均匀的分布在横轴两侧，没有明显的喇叭状，个别点偏离横轴，存在少量异常数据，残差近似服从正态分布。

图4 固定参数模型残差Fig.4 Residual diagram of the fixed parameter model

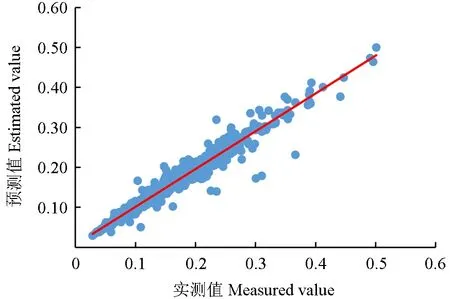
图5 实测值与可变参数模型预测值比较Fig.5 Comparison of the measured value and the predicted value of variable parameter model

图6 可变参数模型残差Fig.6 Residual diagram of the variable parameter model

3.2.2 混合效应模型与哑变量模型的拟合结果

运用R 语言对混合效应模型及哑变量模型进行拟合，拟合结果如表5 所示。混合效应与哑变量模型的拟合精度均高达0.958，混合效应模型与哑变量模型的均方根误差（RMSE）相差不大，但哑变量模型的赤池信息准则（AIC）与贝叶斯信息准则（BIC）均小于混合效应模型，哑变量模型总相对偏差（TRB）和平均系统偏差（MSB）趋向于0，偏差较小，说明哑变量模型较好。采用分径阶的方法对混合效应模型和可变参数模型进行检验，结果如表6 所示，从整体上看，哑变量模型的总相对偏差和平均系统偏差比混合效应模型小，尤其中小径阶效果明显，但在24 cm 径阶中效果不明显，偏差较大。

表5 混合效应模型与哑变量模型的拟合结果Table 5 Fitting results of the mixed effect model and dummy variable model

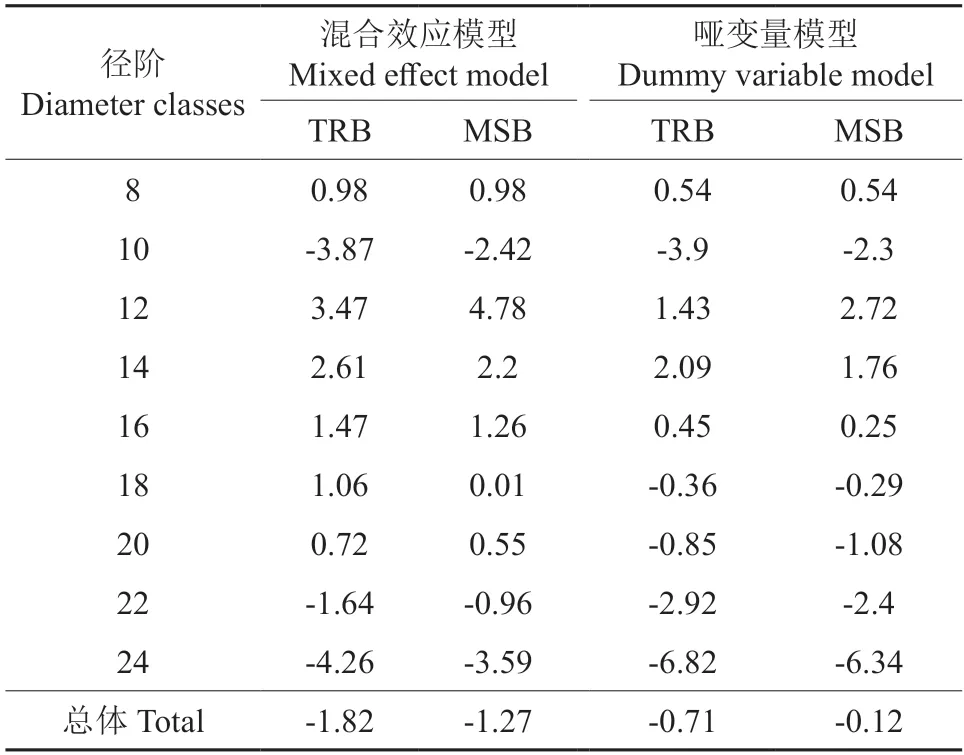
表6 混合效应模型与哑变量模型分径阶检验结果Table 6 Test results of the binary tree volume model by diameter classes

混合效应模型在参数效应和随机效应的方差协方差结构确定后，有2 个问题必须要考虑：一是模型的异方差，二是模型的自相关性[12]。由于本研究的数据不是重复观察的杉木材积数据，所以不需要考虑自相关性。

为了进一步验证混合效应模型与哑变量模型的拟合精度，分别建立了比较图与残差图（图7～10）。

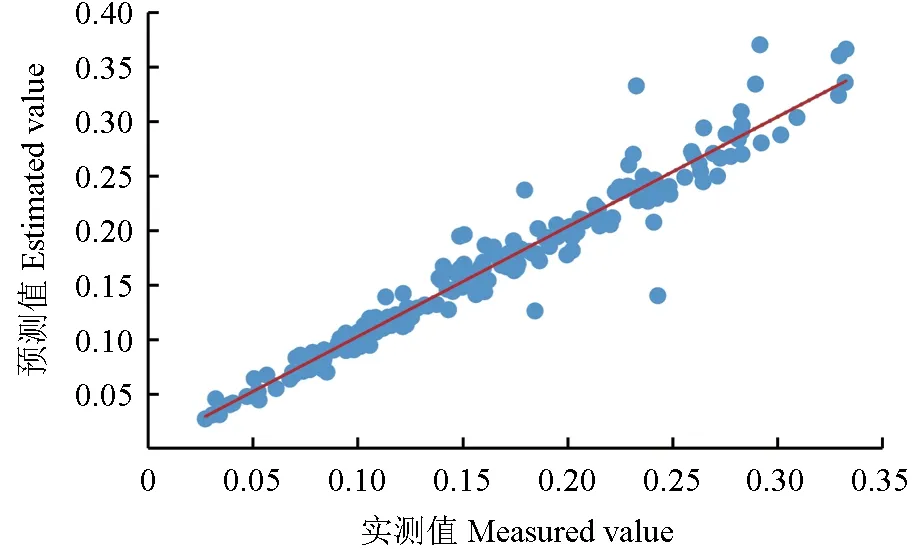
图7 实测值与混合效应模型预测值比较Fig.7 Comparison of the measured value and predicted value of the mixed effect model

由图7 和图9 可以看出，实测值与预测值比较图中离群点较少，拟合精度较好；由图8 和图10 可以看出，混合效应模型与哑变量的残差图没有呈现明显的喇叭状，不需要消除异方差性。

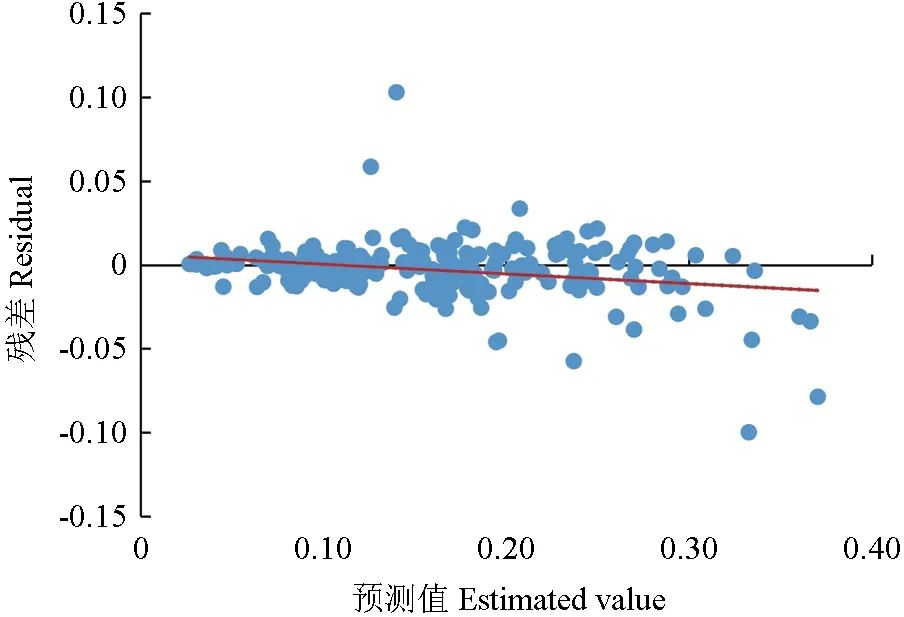
图8 混合效应模型残差Fig.8 Residual diagram of the mixed effect model

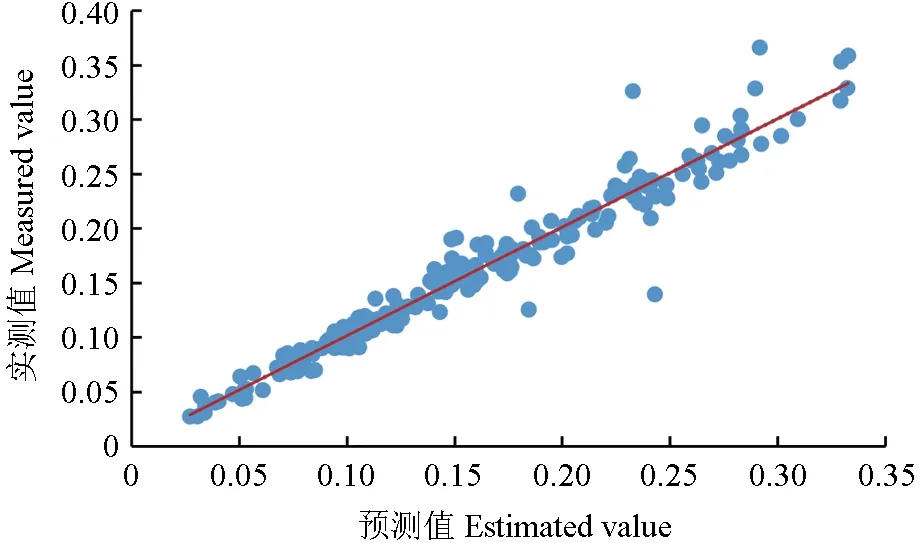
图9 实测值与哑变量模型预测值比较Fig.9 Comparison of the measured value and predicted value of the dummy variable model

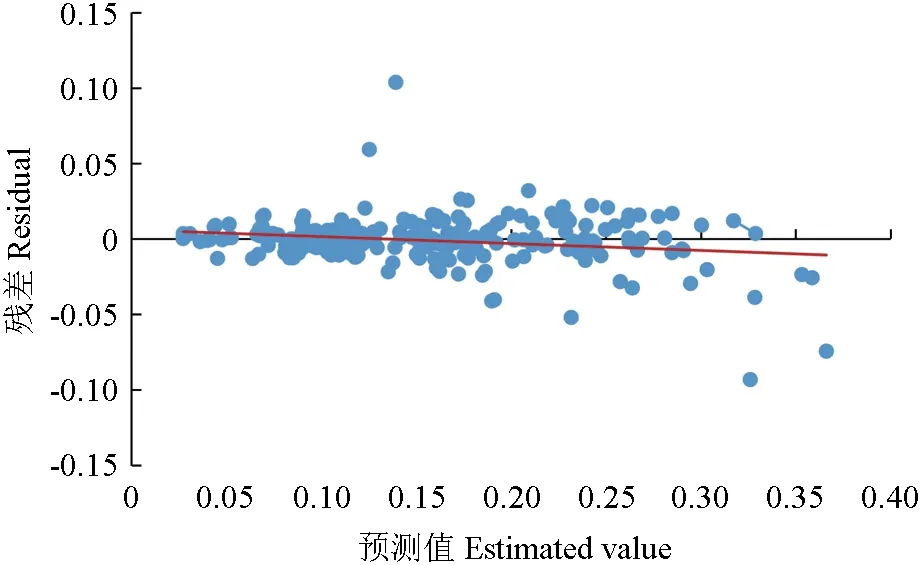
图10 哑变量模型残差Fig.10 Residual diagram of the dummy variable model

4 结论与讨论

4.1 讨 论

无论是编制林业数表，还是估算森林蓄积量，二元立木材积模型都是重要依据，而山本材积式是常用的单木材积计算模型。本研究以山本式为基础模型建立固定参数模型，通过对基础模型的再参数化构建可变参数模型。因立木材积模型受树高和胸径2 个因子影响，存在异方差现象，故对参数估计时采用加权最小二乘法消除异方差性，以对比分析胸径和树高对材积的影响。结果表明，相较于固定参数模型，可变参数模型的拟合精度更高，误差更小。这与诸多学者结论一致，如陈怡[10]、贺鹏等[22]以山本式为基础模型构建可变参数模型，结果表明可变参数模型明显优于固定参数模型，具有更高的预估精度，这是由于树干材积与树高和胸径2 个变量的变化率有关。

考虑到湖南地处丘陵地带，地形地貌复杂，局部区域气候有差异，用常规的回归方法拟合模型的结果存在偏差。本研究以区域作为随机变量和哑变量，分别构建了混合效应模型和哑变量模型，能较好地提高模型精度。如张珍等[23]以不同气象因子为主要预测变量，构建混合效应模型，与Logistic 基础模型相比，拟合精度更高，预测更优。罗洪斌等[24]运用哑变量方法更好地提高了蓄积量的估测精度。Li 等[25]、Ou 等[26]以龄组和冠层密度等为哑变量对生物量进行估测研究，结果表明哑变量的引入可以有效提高估测精度。上述研究表明，混合效应和哑变量模型的引入对提升模型预估精度有效。

本研究通过确定系数、总相对偏差、平均系统偏差、均方根误差、赤池信息准则和贝叶斯信息准则对各模型进行检验与评价，并通过分径阶的方法对各模型进行检验，为选取最优模型提供了较客观的判断依据。在分径阶对各模型进行检验中发现，在24 cm 径阶的总相对偏差（TRB）和平均系统偏差（MSB）均超出±3%的范围，存在一定的偏差。可能因为样本平均径阶样木多，两头的样木比较少，在今后的材积模型中可以考虑通过高径比、径阶或者树高级进行分段建模。

4.2 结 论

本研究以湖南省常德、郴州、衡阳、永州、邵阳、湘西以及益阳地区的采集杉木样本数据为基础，利用固定参数、可变参数、混合效应以及哑变量的方法研建二元立木材积模型，并与现有材积模型进行对比分析，主要结论如下：

1）现有的湖南杉木立木材积模型已沿用40多年，通过配对t检验法对原二元立木材积模型进行检验，经查表后发现与现有的立木材积模型存在显著差异。

2）以山本材积式为模型基础，建立了固定参数模型和可变参数模型，2 个模型的拟合精度均在0.95 以上。从整体上看，总相对误差和平均系统误差均在±3%范围内，可变参数模型的误差趋于0，均方根误差为0.016～0. 017；10 cm 和22 cm 径阶固定参数模型的总相对偏差和平均系统偏差均超出±3%范围；在24 cm 径阶中，总相对偏差高达-8.13%。从整体上看，固定参数模型和可变参数模型的均有较高的拟合精度，可变参数模型的总相对偏差和平均系统偏差较小，明显优于固定参数模型。

3）混合效应模型和哑变量模型的拟合精度均高达0.958，均方根误差都在0.016～0.017，总相对偏差和平均系统偏差均在±3%范围内，哑变量模型的赤池信息准则和贝叶斯信息准则相较于混合效应模型较小；在10、12 和24 cm 径阶混合效应模型的总相对偏差均超出±3%范围，存在一定偏差，而哑变量模型的总相对偏差和平均系统偏差趋于0，模型更优。