“结构化”认知呈现,“后建构”课堂提升
——“锐角三角函数”复习课教学设计及反思
■刘 玉 周同全
一、教学目标
复习三角函数知识点,建构知识网络;利用三角函数解决实际问题。
二、教学重点
判断一个三角形是否可解。
三、教学片段
1.情境再创设,促进认知结构化
师:同学们每天到教室都要爬楼梯,我们前面学过,可以用数学中的什么量来表示楼梯的陡峭程度?
生1:可以用斜坡与水平面的夹角来表示。角度越大,楼梯越陡。
师:最近我们还学过哪个量可以用来表示坡的陡峭程度?
生2:三角函数。
师:具体是哪一个三角函数?
生3:正切。正切值越大,角度就越大,坡也就越陡。
师:说得非常正确。今天,我们一起来回顾三角函数的相关内容。
设计意图:让学生感悟数学与实际生活的紧密联系,培养学生用数学的眼光看世界。
2.概念再梳理,促进知识结构化
问题1:沿着一条上山直道行走,每前进100m,上升的高度为50m。(1)这条直道的坡度为;(2)求坡角的正弦、余弦;(3)坡角度数为。
师:解决这个问题,我们首先要做什么准备工作?
生4:画图,求出另一条直角边的长度。
师:请同学们画好图,并由第一小组同学来回答。
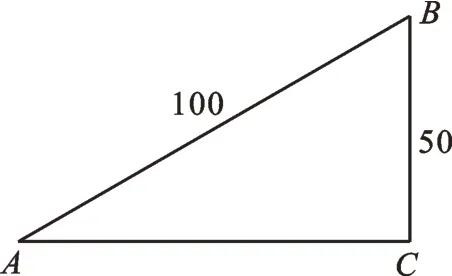
图1
生8:坡角是指斜坡与水平面的夹角,因为坡角的正弦为
师:很好,我们来看第二题。
问题2:如图2,在△ABC中,∠ACB=,过点C作CD⊥AB于点D。

图2
师:BC的长度怎么求呢?
生9:直接利用三角函数来求。因为在Rt△ABC中,所以BC=12。
师:借助直角三角形,我们可以用三角函数求线段长。tan∠ACD该如何求呢?
生10:借助Rt△ACD,求出AD、CD即可。
师:AD、CD分别如何求?
生11:可以利用勾股定理先求出AC,然后用等积法求出CD,再用勾股定理求出AD即可。
师:有没有同学有其他想法?
生12:因为∠B和∠ACD相等,所以可以求∠B的正切,这样只要求出AC就可以了。
师:两位同学给出了两种不同的方法,也就是说我们求一个角的三角函数值,可以直接求,也可以找一个与其角度相等的角替换。比如本题,我们用的是同角的余角相等。那么,两种方法分别在什么时候用呢?
生13:我觉得当一个角的三角函数不易求时,可以将其转化成相等的角来求。
师:那你能想到的转化方式有哪些?
生14:同角的补角相等;由平行线得角相等;同弧所对的圆周角相等。
师:还有补充的吗?
生15:全等、相似中,对应角相等。
师:同学们考虑得非常全面,这都得益于你们平时的积累和反思。现在,我们再来看第三个问题。
问题3:如图3,为测量建筑物AB的高,现在地平面上取一点C,测得A点的仰角为45°,再向前走20m,取一点D,D在BC延长线上,测得A的仰角为30°,已知测量仪高1.5m,求AB的高。

图3
师:哪个角是45°?哪个角是30°?
生16:∠AEG=45°,∠AFG=30°。
师:能直接求出AB吗?
生17:不能,要分成两段,即AG和BG。
师:AG能直接求出吗?
生18:不能。我们可以设AG为x,通过三角函数表示出EG和FG,进而表示出EF,这样就能构建关于x的方程,从而求出AG。
设计意图:从简单问题入手,让学生体会解决三角函数问题必须借助直角三角形;利用不同方法求解,提高学生的解题技巧,发展学生的逻辑推理和直观想象力;回顾一些基本图形、解决策略,利用观察、画图、计算等,使核心素养的培养真正在课堂中发生。
3.方法再运用,促进技能结构化
师:以上问题我们都是借助现成的直角三角形来解决的。如果在非直角三角形中,我们又该如何解决呢?请大家看题。
问题4:如图4,在△ABC中,∠C=150°,,求BC。

图4
师:BC不在直角三角形中,如何求呢?
生19:可以构造直角三角形。
师:如何构造?
生20:过点C作AB的垂线CH,把BC放在直角三角形BCH中求。
师:能求吗?我们讲过,解直角三角形要知道除直角外的两个元素,而且至少要有一条是边,条件告诉了我们,那BH或CH能求吗?
生21:不能。可以过点A作AH⊥BC。
师:能说说你的理由吗?
生21:这样可以把∠B放在Rt△ABH中,∠C的补角是30°,在Rt△ACH中,我们可以先求AH、CH,再求出BH,从而求出BC。
师:那请同学们顺着他的思路求BC。通过分析、求解这题,你对于求非直角三角形中的线段,得到了哪些经验?
生22:要把非直角三角形转化成直角三角形。
师:怎么转化?
生23:过顶点作对边的高。
师:任何顶点都可以吗?
生24:不能破坏题中的特殊角。
师:怎么才能做到不破坏?
生25:过非特殊角的顶点作高。
师:你认为哪些角是特殊角?
生26:30°、45°、60°。
师:还有吗?
生27:还有已知三角函数的角和一些钝角,如120°、135°、150°。
师:这些角怎么用呢?
生28:我们可以用它们的补角。
师:刚才同学们分析得非常到位。对于非直角三角形,我们有了处理的策略,那在四边形中又该如何求线段的长度呢?
生29:转化成三角形……
设计意图:教师通过提出问题串,提升学生的解题技能,让学生明确解斜三角形需要知道三角形的三个元素(至少有一条是边),培养学生的模型思想和转化思想。
四、教学反思
课堂是师生共同完成的一项劳动,而这项劳动成功与否,师生关系是关键。体验式学习是以“后建构主义”理论为指导的,其成效尤其显著。但是,在实践中,教师常常不能很好地把握课堂教学时间,不能让学生自由地表达意见。因此,教师需要运用各种教学手段构建一个高效的数学课堂,充分发挥学生的主观能动性,激发学生的学习热情,从而提高课堂效率。此外,在课堂上,教师应积极引导学生进行思维分析,剖析典型问题,使学生积累经验,以解决问题。教师在选择“材料”,创设体验场景时,要注重学生思维的深度生长。
教育是一个长期奋斗、不断优化的认知过程。因此,在今后的教学发展中,教师要不断地寻求有效的教学策略,主动建构学生的主体意识,促进学生核心素养的发展。

