基于单片机的纸张计数显示装置的设计与实现

吕美萱, 孙志刚,2, 张 敏 , 兰国强, 王国涛,2

(1.黑龙江大学 电子工程学院, 哈尔滨 150080;2.哈尔滨工业大学 电器与电子可靠性研究所, 哈尔滨 150001)

0 引 言

在21世纪工业大规模生产背景下,纸张计数显示装置可运用于机器设备和公司数纸器中的计数模式中,在印刷以及包装行业应用十分广泛。如工业生产纸张进行售卖,应用纸张计数器即可对固定要求的纸张数目进行包装,不仅大大节省了人力,而且能保证计数的准确性,同时对相关检测机器的设计提供了一定的参考价值。传统的纸张计数形式主要有人工计数、直接侧面拍照法以及机器视觉间接计数等方法,但都存在不准确的问题。如传统的机械直接查数或人工计数方法受主观因素影响较大,需测量纸张堆叠后总厚度除以单张纸厚度,测量方式不便捷且效率低下[1-2]。直接侧面拍照法通过对所测纸张的侧面进行拍照,再依据页与页的边缘线数量来计算纸张数量。不仅对所选摄像头的像素有很高的要求,而且图像处理技术也需要满足一定的条件,最终所得纸张的测量准确度并不高[3]。基于机器视觉的间接计数法对纸张厚度和边缘质量要求较高,且需要对图像特征进行分割,存在分割阈值选取不易及计算慢的特点[4]。因此传统的纸张计数设计方法已无法满足现代社会对纸张计数测量的要求。

近年来,有学者利用更加新颖的方式实现纸张计数。目前,国内产生的软硬件结合设计的方法相对较多,如王建卫等设计的基于LM331电路的纸张计数系统[5],选用NE555模块形成振荡电路,利用LM331频率电压转换电路将频率变化转换为电压变化,再经ADC0809实现数模转换,计数最多可达到89张。李红等设计的基于STC89C52的单片机纸张计数系统,利用单片机定时功能及一次回归来实现频率计数1～10张纸张的测量,利用二次回归函数实现了测量大于15张纸的计算公式[6]。本设计与其部分思想相似,即只用一次回归并使用分段拟合方式进行估算,且利用卡尔曼滤波算法对系统进行优化处理。王瑞琦等设计的基于FDC2214模块的纸张计数系统[7-8],通过测量LC谐振回路直接将电容量转化为数字量,并以0～3.3 V的电压值传送给单片机AD模块,使单片机读取到容值。通过电容传感器公式直接计算出总体纸张厚度,模块精度高,测量准确。陶冶博等设计的基于555芯片及等精度法测频的纸张计数装置,引入自校准功能减小误差,通过最小二乘拟合获得最终换算公式,可实现1～50张纸的精确测量[9]。Qin等设计了一款基于STM32的纸张计数显示系统,具有显示纸张数量并通过语音宣布的功能,利用统计原理减小线性误差,提高了区分纸张数的准确性[10]。Zhou等以STM32H743处理器为核心,采用无桥轴的方法测量纸板之间的阻抗,通过16位高精度AD精确采样被测阻抗及两端电压的相移和幅值,计算出板间对应容值,再根据电容值与纸张厚度的反比关系,实现了对纸张的精确测量[11]。Li等同样以STM32为核心板,通过FDC2214模块采集两板间电容值,通过IIC串行总线传输给MCU控制器,实现纸张计数功能[12]。Wang等为了提高纸张包装精度,设计了一种基于STC12LE5A60S2和电容传感器芯片FDC2214的纸张计数显示装置,利用回归算法进行线性拟合,最大测量范围可达到0～70张A4纸[13]。

一些实现纸张计数功能的算法也逐渐涌现出。龙永红等设计出一种基于空间和灰度特征的粗精二级算法,可用来测量纸张数量[14]。Chen等基于Gabor滤波器设计的纸张计数算法,通过对纸张条纹进行提取,建立不同频率的滤波器,采用灰度差分法计算纸张数量[15]。随着信息技术的快速发展,逐渐又出现了用图像、超声波、电磁、红外和射线等方法进行纸张计数,但大多数生产成本较高,且设备的功能结构复杂[16]。因此,设计一套性价比高且适用范围较广的纸张计数系统或装置显得尤为重要。

在总结现有研究基础上,寻求一种新方法来完成对纸张进行简便高效测量的任务,并由此设计了一款基于单片机的纸张计数显示装置。以STM32单片机为核心,采用555定时器与RC电路组成多谐振荡电路,对两块平行极板间给定纸张数实现测量及显示被测纸张数量的功能。规模简单且性价比高,能保证纸张在未被损坏的前提下自动快速对纸张进行安全计数,并将纸张数量显示在OLED显示屏上,具有无污染、无噪声和效率高等特性。

1 硬件设计

系统以STM32F407为主控制器,利用RC电路电容充放电原理,使555定时器振荡从而产生一定频率的方波,将两极板间所需求得的电容值C当作输出一定大小频率的方波所需要的电容值,即可将极板间电容与555定时器建立一定函数关系。由于纸张数量与频率呈线性关系,经过线性拟合找到满足两者成立线性函数关系式的未知数,通过找到频率对应纸张数量的拟合关系式,即可通过频率大小间接测量纸张数目。通过编写程序控制主控芯片,完成输入捕获、IIC通讯协议、串口通信、卡尔曼滤波和测量显示任务。显示模块使用OLED显示屏,可显示汉字、字母、字符串和特定图片等内容。时钟电路给单片机提供时钟信号,复位电路可以实现对系统实现复位以保证单片机正常工作。由于555定时器输出波形不理想,为尽量克服吉伯斯现象,本设计在电路输出端接入施密特触发电路,使得输出波形尽可能接近于理想方波。

1.1 微处理器的论证与选择

1.1.1 8051单片机

传统的51单片机为8位机,价格便宜,控制简单,但算力不够,容易造成计算缓慢、代码过长内存不够放等问题,片内资源较少,难以存储大体积程序和实现快速的反应控制,受时钟限制精度不高,外围电路也增加了系统不可靠性,且在调试中容易出现界面卡顿和未响应的情况。

1.1.2 STM32单片机

STM32开发板是ARM公司在Cortex内核基础上进行开发的一款芯片,主频高达168 MHz,支持浮点运算和DSP指令,具有成本功耗低、性能高的优点,内置1 M字节的Flash,256 kB的RAM且提供多个外部存储控制器接口。为保证系统的测量精度,微处理器选用STM32F4ZGT6开发板。

1.2 纸张计数系统检测方案选择

1.2.1 运用NE555测量RC电路充电时间求电容

定时器由NE555及其外围电路构成完整的应用电路。555定时器接通电源后有两个暂稳态,此方法同样运用电容充放电原理。因此电容充放电速度与R、C值相关。由于待测电容远小于分布电容值,即分布电容对被测电路电容值无影响,因此放电时间不对装置造成影响,故只需要对其充电时间进行测量,即可知道容值大小[17]。但当电容值较小时,充电时间会很短,导致难以测量准确,故不采取。

1.2.2 运用AD/DA转换测量容抗求电容

容抗Xc和容值C的函数关系式为:

(1)

首先,让DA转换器产生正弦波,频率自控,将正弦波输入至电容极板,由于电容具有通交隔直的功能,于是此时通过电容的正弦波只剩下交流电,其次通过AD转换器对交流电流进行采样。由于交流电流和交流电压具有不稳定性,此处将电机思想运用至电容测量过程中,运用帕克变换可将交流电压和交流电流全部变为直流,利用欧姆定律,此时的电阻R就等于回路中的容抗值。求出容抗值后即可求出电容值。此方法虽原理可行,但实践过程中难度较大,变量不好控制,故不采取。

1.2.3 运用NE555测量方波频率求电容

使用RC电路和555定时器组成的多谐振荡电路,多谐振荡器是矩形波发生器,利用电容充放电原理,使电路振荡产生一定频率的方波,频率大小与电路中的R和C值密切相关。若将两极板间所需求得的电容值C当作定时器输出一定大小频率的方波所需要的电容值,就可以将极板间电容值与555定时器建立一定函数关系。再利用线性回归分析对频率与纸张厚度进行拟合,最终可测得纸张数量。

综上分析,利用方波频率特性,找到拟合函数,确定纸张数量,故选择用NE555测量方波频率求电容。

1.3 纸张计数检测单元

纸张计数是整个系统中最重要的环节,其中数据的及时性和准确性直接影响着整个系统的效率和准确度[3]。装置所依靠的开发环境为Keil5,使用C语言进行程序的编写。程序编写模块为输入捕获程序、IIC通讯协议、PL2303HX串口模块通信及OLED显示程序。

1.3.1 纸张计数系统结构工作原理

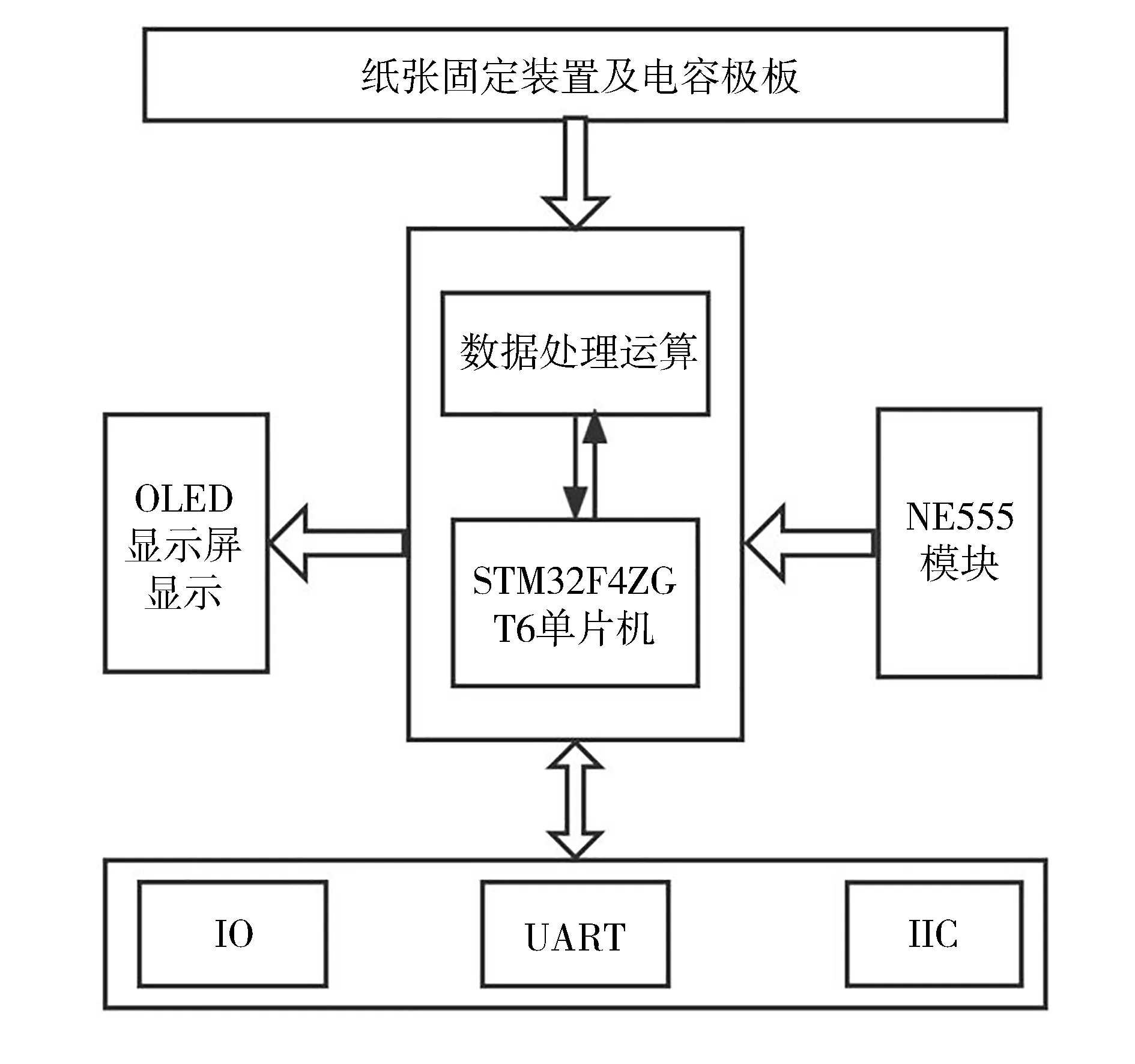
图1 纸张计数器系统硬件框图

图2 纸张计数器系统框图

1.3.2 NE555模块及系统参数选取

多谐振荡器是一种自激振荡器,在接通电源后不需要外加触发信号,便能自行产生具有一定频率和一定脉宽的矩形波发生器[19]。矩形波中包含丰富的高次谐波分量,多谐振荡器没有稳定状态,只有两个暂稳态[20]。利用RC电路和555定时器组成的多谐振荡电路,不需要外接触发信号,通过两个比较器C1、C2的输入端分别与1/3Vcc和2/3Vcc进行比较,实现电源经R1、R2向电容C充电,以及C通过R2和放电管放电,使电路产生振荡。方波从555定时器出来以后经过波形整形电路后直接送入单片机,由输入捕获测出两个上升沿之间的距离,即读出方波一个周期的值,进而能够知道方波的频率大小,通过这样方式不断增加纸张数量进行若干次重复测量。

具体作法为:第一步进行数据处理,将纸张数量进行分段拟合,计算张数,将拟合函数关系式确定好写入程序,放入纸张到两极板间后,单片机就会按照公式计算当前频率下对应的纸张数量,再通过OLED显示屏进行显示。

在关键参数的选取方面:

首先,在输出方波频率范围选择方面,输出方波的频率范围是由R1、R2的值和极板间电容确定的。纸张增加引起的电容改变在电路可辨识的范围内。由理论计算和实际测量得到最低振荡频率在 2kΩ 以上,所以在振荡器接一个高通滤波器,然后经过比较电路整形[21]。其次,在R1、R2固定电阻值与电容C的选取方面,经过多次深入实验,所发现的规律为R1与R2越大,相同的电容值测出的频率就会变小,而电容C若过大可能导致无法测量,所以将C设定为0.01 μF。对于电阻的选取,既要满足让实验及时看到变化,又不能变化太大,所以分别选取了160、180和200kΩ电阻作为回路电阻值,经实验发现三者都满足实验要求,最终选定160 kΩ作为R1和R2的电阻值。最后,在电容极板的选取方面,采用导电效果好,廉价实惠的双面覆铜板作为极板,信号传输效果好,易操作。本实验选用两片覆铜板作为电容平行极板。

1.3.3 多谐振荡器振荡周期估算

由工作原理分析可知,电容充电时间tw1如式(2)所示,即电容电压V从1/3Vcc上升到2/3Vcc所需时间。电容放电时间tw2如式(3)所示,即电容电压V从2/3Vcc下降到1/3Vcc所需时间,电路稳定工作后,电路的振荡周期T如式(4)所示。

(2)

(3)

T=tw1+tw2≈0.7(R1+2R2)C

(4)

1.3.4 纸张计数系统测量电路

基于单片机的纸张计数器电路如图3所示。施密特触发电路:多谐振荡器理论上的充放电时间是理想的,但在实际中,由于电源波动、电容充放电误差以及电阻值误差等因素,输出波形的频率准确度和稳定度会受到较大影响。因此为减小误差,提高频率稳定度,要选用精度高的元器件,电源电压波动尽量小。为尽量克服示波器中的吉伯斯现象,使得方波输出较为理想,本设计将在输出端接入一个型号为SN74LVC2G17DBVR的施密特触发电路,能把变化缓慢的波形变换成矩形脉冲,这样输出波形比较接近理想的方波。

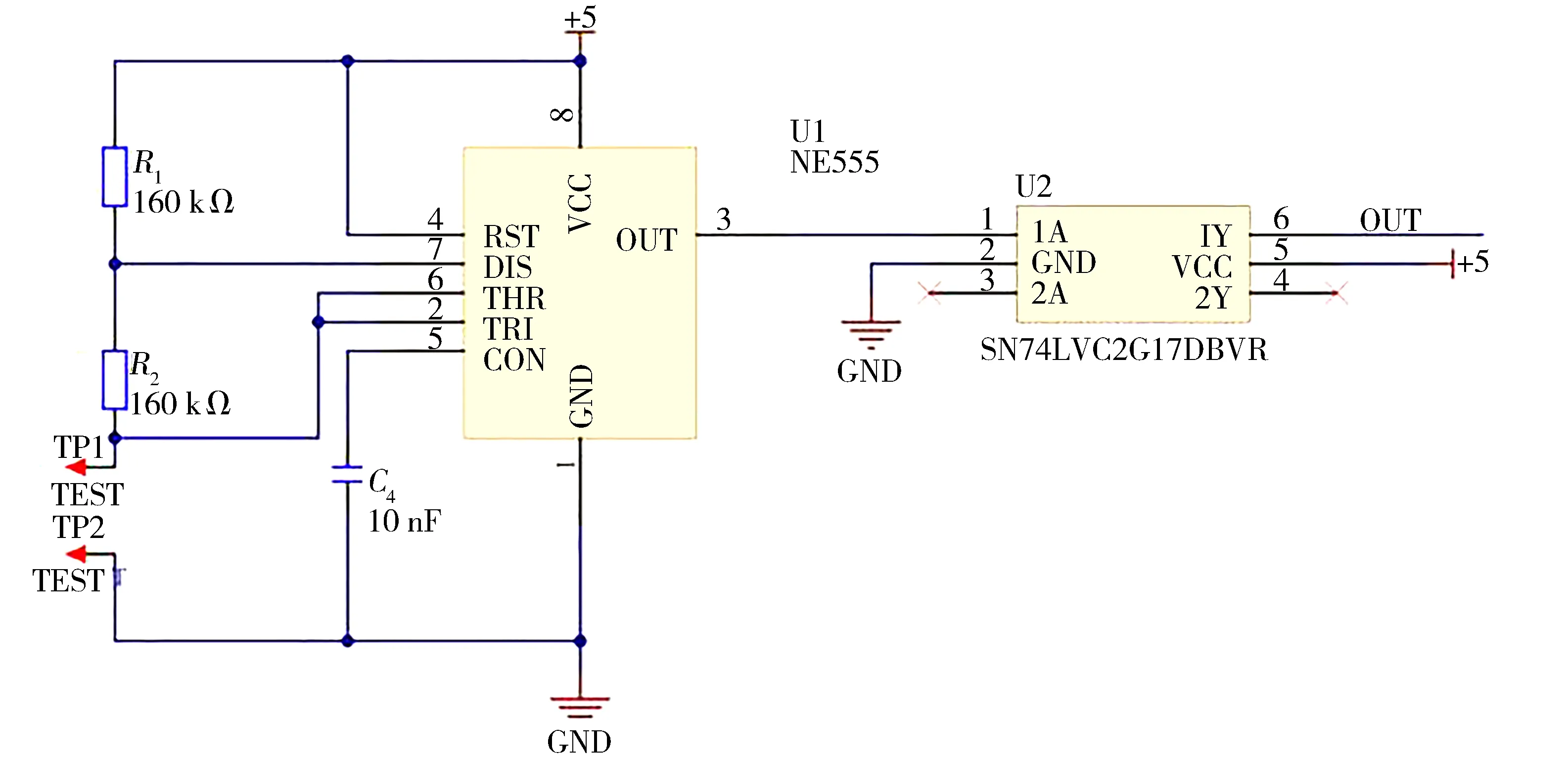
图3 基于单片机的纸张计数器电路图

若输入信号是一个顶部和前后沿受干扰而发生畸变的不规则波形,可以适当调节施密特触发电路的回差电压,得到整齐的矩形脉冲[22]。在实验过程发现,将施密特触发电路作为整形运用时,需要适当提高回差电压才能得到较好的整形效果。如果回差电压较小,则整形效果较差,而且可能产生错误输出。回差电压过大,会降低触发灵敏度,因此折中选取。

1.3.5 纸张计数极板及固定装置

由于电容的特性,面积、间距、介质都会对系统参数造成影响,测量时两极板必须能压紧或夹紧被测纸张,且纸张不能移动或松动。纸张是微弹物质,压紧与不压紧是有一定区别的,因此为保证两极板相对面积保持不变,本设计自行采用仿机械固定,选用箱子搭建出一个U型底座,箱子两边固定一对长约20 cm的对称滑轨,选用两块亚克力板分别粘贴两片电容极板,将一块亚克力板置于箱子底部,另一块亚克力板上方粘贴一段长约20 cm的木条,选用两个木条分别被固定于一对滑轨之间的上下处,用于上下滑动,每次拉住上方木条就可提起上电容极板,此设计方法一定程度上可以保证每次取放有很高的相似度。为确保纸张被夹紧,将木条上方固定一个重物块,选用锤头作为此重物。至此装置搭建完毕,可确保每一次加入纸张都可实现两极板间面积不变且纸张被夹紧的任务。

2 软件设计

纸张计数系统运行流程具体为:首先,对系统进行变量初始化。开启单片机输入捕获功能。然后,开始放入纸张,当单片机第一次检测到方波的上升沿时,定时器开始计时,直到第二次检测到上升沿为止,定时器停止计时并结束中断。其次,将得到的周期值T利用数学公式转换为频率,上位机将实时显示频率波动范围。接着,对系统进行卡尔曼滤波,使频率波动范围降到最小。最后,OLED显示屏结合拟合函数显示被测纸张数量。通过此流程可进行若干次重复测量。

2.1 程序功能描述

程序中主要包括数据处理控制程序和显示程序。数据处理控制程序包括输入捕获程序、IIC通讯协议、串口通信。首先由单片机对555电路方波进行输入捕获测得两个上升沿之间的距离,即一个周期T的时间,然后换算为频率,下载程序至单片机后,可连接串口模块通过上位机实时接受纸张频率数据显示波形信息,最终使用IIC通信协议使单片机与OLED显示屏进行关联。

显示程序包括OLED文字显示和上位机波形显示。装置可精准测得给定的纸张数目,通过OLED显示屏显示出所测纸张的数目,屏幕显示文字为“共计数:xx张纸”,通过使用取字模软件实现此项功能。在测量系统频率时利用串口接收数据并通过上位机显示波形频率数据,通过增加纸张数目,可观测到1～30张纸张的频率变化。

上位机显示的三个波形分别为原始波形、经加权平均滤波后波形和经卡尔曼滤波后波形,通过横向对比卡尔曼滤波及加权平均滤波后的波形结果,选出最合适系统测量的滤波算法,评价指标为频率浮动范围,范围越小代表滤波效果越好,测量准确度越高。

2.2 纸张计数系统误差分析

在测量过程中,由于外部环境干扰或系统自身引起的零点漂移都会造成一定的测量误差,人体自身所带的磁场也会影响极板间电荷分布,由于所测数据的要求精度较高,将有面积、间距、温度和介质等因素的影响,以下3项因素对装置影响最大:

(1) 面积影响: 极板间的电容值受到电荷分布的影响,当两极板间发生上下错位、互不平行时测量数据一定不准确,因此要做到使板子固定且相对面积保持不变,又能塞入纸张,在固定铜片位置时一定要认真。

(2) 间距影响: 纸张为微弹性物质,随着纸张数量增加,纸与纸之间的间隙也在逐渐增大,压紧与不压紧是会影响到测量结果的,国际标准A4纸纸张厚度为0.104 mm。除去铜板夹紧的部分,其他部分间隙会更大,最终导致测量的厚度不再是一张纸的厚度,这就会造成电容值发生跳变,进而导致电路中频率跳变,因此硬件设施上减少误差的方法为在极板上放置一些重物。

(3) 介质影响: 纸张新旧程度、周围环境温湿度、纸张材料、极板吸附杂质和通电情况下加速氧化等都有一定的影响。新纸比较平滑,外表面积小。旧纸比较粗糙,外表面积比新纸大。环境温湿度会造成电容产生温漂,极板在被触摸后会吸附手上的杂质,这也会造成偏差,往往这点最容易被忽视。

2.3 滤波优化算法的论证与选择

纸张计数器原始频率波形如图4所示,可发现频率波动范围为34.5～35.7 kHz,波形上下浮动范围较大。

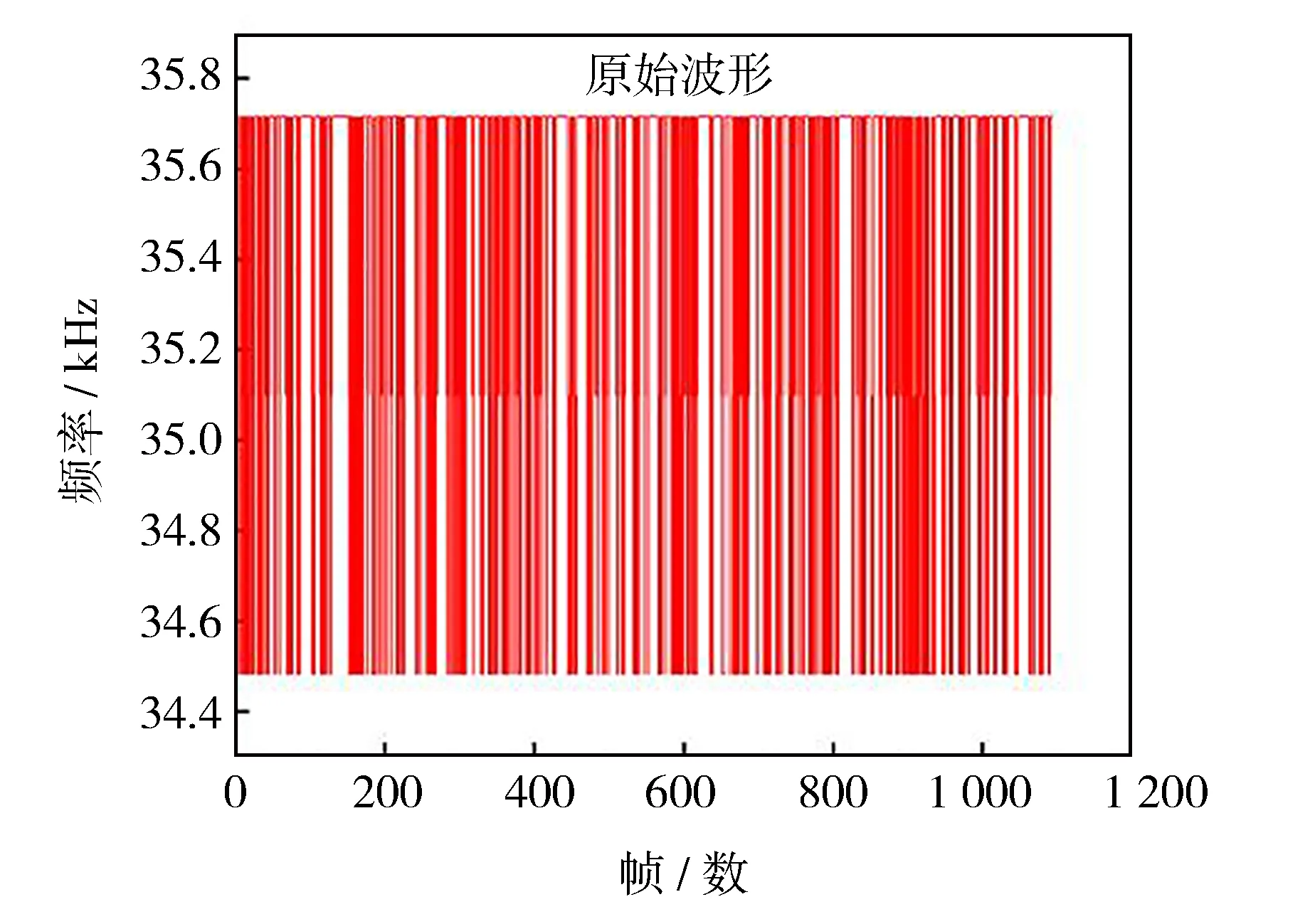
图4 纸张计数器原始频率波形

2.3.1 加权平均滤波

在间距的处理上,需使用一定的滤波算法进行数据优化。加权平均为利用过去若干个按照时间顺序排列起来的同一变量的观测值并以时间顺序变量出现的次数为权数,计算出观测值的加权算术平均数如图5所示。在使用加权平均滤波算法时,根据观察频率波形可知,在仅考虑间距的状态下,下一秒的频率值永远比上一秒的频率值更准确,即下一秒被压的纸张状态肯定比上一秒被压的状态更真实,数据应是更可信的,因此采用分配权重的方式给不同时间,使得下一秒权重更大,上一秒的权重更小。此算法的优点为不会直接提取5个数据总和求平均,而是根据数据的权重来综合判断。上位机中显示的系统经加权平均滤波后的波形如图5所示。在此种算法中设定为1 s,共采集5个数据,5个数据有着不同的权重值分别为:第一秒,0.1;第二秒,0.1;第三秒,0.2;第四秒,0.3;第五秒,0.3。权重总和为1,新数据一定是这5个数据的加权平均值。

图5 纸张计数器经加权平均滤波输出频率波形

2.3.2 卡尔曼滤波

由于系统扰动不可控、很难建模,不存在完美的数学模型且测量传感器存在误差,卡尔曼滤波器递归算法能够很好的推断出实际发生状况,它不仅轻量化,消耗极少的内存,而且速度非常快,适合对实时问题和嵌入式系统的处理。对于卡尔曼系统而言,只要是存在不确定信息的动态系统,它就可以对系统下一步的动作做出有根据的推测,因此,系统采用卡尔曼滤波对噪声进行滤波,计算步骤为:先估计某一时刻的状态,再将测量中发现的含噪声变量进行反馈,因此它分为时间更新和测量更新两部分。上位机中显示的系统经卡尔曼滤波后输出波形如图6所示。通过对比可得出结论:加权平均滤波适用于较大纯滞后时间常数的对象,缺点为不能迅速反应系统当前所受干扰的严重程度,滤波效果差。卡尔曼滤波的优点在于能够巧妙融合观测数据与估计数据,对误差进行闭环管控,将误差限定在一定范围。所以最终选用卡尔曼滤波器进行滤波。通过3个波形综合观察可以看出,卡尔曼滤波非常平滑,误差最小。

图6 纸张计数器经卡尔曼滤波输出频率波形Fig.6 Paper counter output frequency waveform by Kalman filtering

2.3.3 关于卡尔曼滤波参数Q、R和P的取值

Q和R是历史测量值与当前测量值的加权,稳态时可以分析系统的频域特性。Q为过程噪声协方差,越小系统越容易收敛。R为观测噪声协方差,太大或太小都不一定合适。可选搭配包括:R固定,Q越大,代表越信任测量值,Q无穷代表只用测量值。反之,Q越小代表越信任模型预测值,Q为零则是只用模型预测。考虑到卡尔曼滤波需要根据调参来选出最适合系统的数值,测量时,先将Q从小向大调整,将R从大向小调整,固定一个值再调整另一个值,经过多次实验,调得参数为:Q=0.000 5,R=0.543。

系统中的P值代表误差协方差初始值,表示对当前预测状态的信任度,P越小,即越相信当前预测状态[23],它的值决定了初始收敛速度。开始时设置一个较小的值,以便于获取较快的收敛速度,因此P值设置为0.02。

2.4 线性回归分析

本研究采用最小二乘法估计线性回归方程,由多谐振荡器周期估算可知,纸张厚度d引起两极板间电容值的变化,进而影响电路振荡周期T,即影响电路整个频率,因此由现有关系式,找到首尾变量关系,中间多个变量的值不考虑,在R1和R2电阻值固定的情况下,由公式(5)可知:

(5)

由于频率f和纸张厚度d的测量趋于一元函数,利用数理统计,根据最小二乘法对线性回归方程的定义,可得公式为:

(6)

(7)

(8)

3 系统测试及分析

3.1 纸张计数器硬件测试

由于影响电容式传感器的因素较多,因此先采用分模块的方式进行分别调试,再进行整体的系统测试。如图7所示为基于NE555模块及STM32单片机所构成的纸张计数显示装置系统,其中包括单片机与测量电路、单片机与OLED显示屏、单片机与串口的连接方式以及在测量纸张时向上提起装置的过程。

图7 纸张计数器显示装置系统

3.2 纸张计数器软件测试及结果

本装置所依靠的开发环境为Keil5,使用C语言进行程序的编写。程序编写模块为输入捕获程序、IIC通讯协议、串口通信及OLED显示程序。电路连接好后首先将程序下载到32单片机中向两电容极板间放入一定数量的纸张,进入调试并观测上位机输出的周期波形及OLED显示屏显示出的纸张数量,观测结果,可对测得的结果进行记录。表1为3次进行1～30张纸的频率测量。可以发现,随着纸张数量的增多,频率也在逐渐增大,但在同一次实验中测得的频率值相差也较大,这可能是由于装置自身或人为因素的干扰。在表中未列出的数据中,发现当纸张增加到一定数量时,将测得频率和相应纸张厚度代入表达式后,等式不成立。一方面是因为实际实验并非在理想环境下,所测结果与理论值是存在误差的,另一方面是因为纸张数量增多时,纸与纸之间的空隙也在逐渐增大,导致纸张真正的厚度被掩盖了,进而影响频率变化。表2为对1～30张纸纸张测量的结果,可以发现,纸张数量在1～10时,测量正确率为80%,在10～20张和20～30张时,测量正确率为20%,表明纸张在达到一定数量时,由厚度直接引起的对装置测量结果的影响比较大。

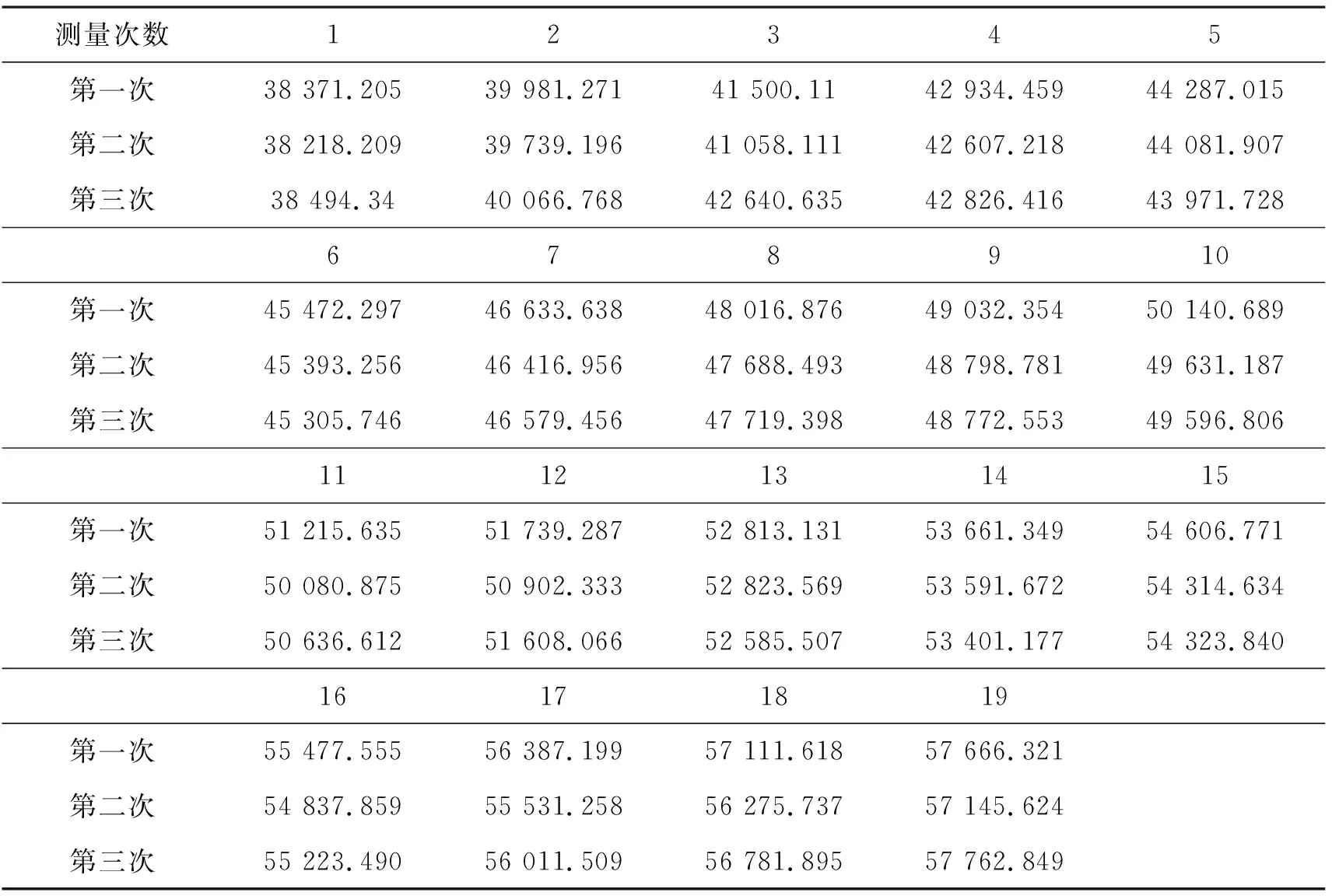
表1 1～30张纸测量数据 / Hz

表2 测量结果分析

3.3 纸张计数系统指标参数测试

本次测试采集的频率f(单位kHz)与纸张厚度d(单位mm)可以根据线性回归方程来处理,测量函数为f=ad+b的一元函数类型。为减少纸张过大所引起干扰,测试选用A4纸的四分之一大小进行测量,一张纸的标准厚度为0.104 mm。以下仅列举对1～30张纸选用以上测量次数中的一组数据进行的拟合函数分析。在相关性程度方面由SPSS Statistics模型分析数据可知,模型汇总表中的相关系数R值为0.989,说明频率和纸张厚度存在很强的相关性。在回归效果评估拟合优度方面,线性回归效果的评估主要看R2,表示回归直线和样本观测值的拟合优度。如表3所示,这里R2为0.978,说明了97%的频率变化可以由纸张厚度解释。

表3 1～30张纸数据拟合模型摘要

回归模型的显著性检验:方差分析中,主要看F值及其对应的p值。如表4所示,p=0,小于显著性水平0.01,因此可以认为该回归模型在0.01的显著性水平下显著。

表4 1～30张纸数据拟合方差分析

回归模型的显著性检验t检验:如表5所示,自变量对应的概率值p=0,小于显著性水平0.01,因此可以认为在0.01显著性水平下,自变量d与因变量f存在显著的线性关系。

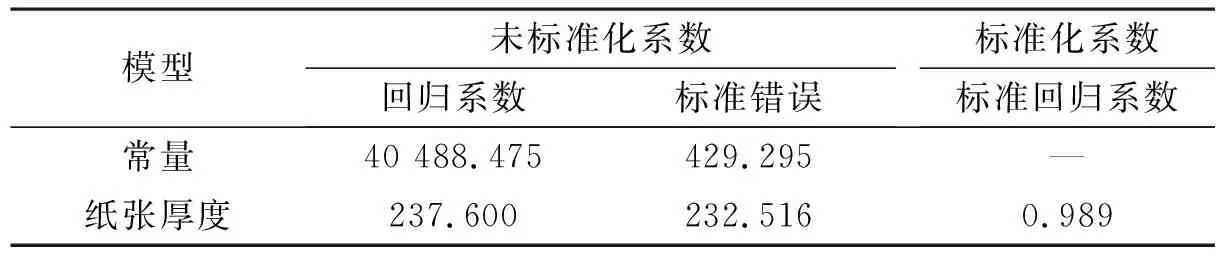
表5 1～30张纸数据拟合系数

3.3.1 纸张计数系统测试结果分析

该系统方案可以用555定时器方波频率来进行纸张数的计数。如表5所示,通过将以上数据经SPSS数据分析后可知,常量b=40 488.475,斜率a=8 237.600,因此1～30张拟合的最终回归方程为:f=8 237.600d+40 488.475。0～30张纸拟合曲线图如图8所示。可看出拟合效果并没有特别好,因此接下来系统采用分段拟合的方式对0～30张纸进行数据拟合。

图8 0～30张纸拟合曲线Fig.8 Fitting curve of 0～30 sheets of paper

3.3.2 线性拟合改进模型测评

装置采用SPSS数据分析软件进行分析。由上述分析可知,1～30张纸张的频率与厚度拟合效果是基本呈一元一次函数的线性拟合,但在实际实验过程中验证到,随着纸张数量逐渐增加,频率是逐渐增大的,如果1～30张纸张只用一个拟合函数来计算,最终所测得的结果只有部分纸张数目准确,OLED显示屏的纸张数往往会因装置的细微变化和拟合函数的精度问题出现摇摆不定现象。因此,对拟合方式加以改进,即对0～5张、6～10张、11～20张、21～30张进行分段拟合。评价指标与上述参数相同,这里不作过多介绍。以下分别是拟合的不同纸张对应的回归方程及系数,0～5张拟合曲线如图9所示,6～10张拟合曲线如图10所示,11～20张拟合曲线如图11所示,21～30张拟合曲线如图12所示。

图9 0～5张纸拟合曲线

图10 6～10张纸拟合曲线

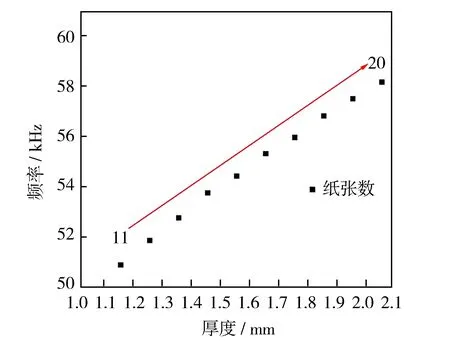
图11 11～20张纸拟合曲线

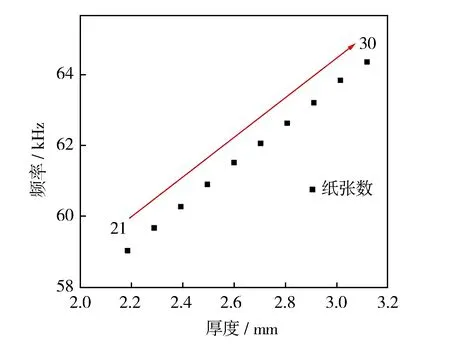
图12 21～30张纸拟合曲线

由上述分析数据可知:0～5张纸拟合直线方程为:f=16 215.621d+36 363.352,如表6所示。6～10张纸拟合直线方程为:f=13 043.462d+37 093.794,如表7所示。11～20张纸拟合直线方程为:f=7 851.032d+42 172.848,如表8所示。21～30张纸拟合直线方程为:f=5 689.734d+46 676.673,如表9所示。经多次实验发现,只有在10张纸以内,测得的纸张数量较为准确,10张以上只有部分纸张数量测量准确,即观测到的拟合函数呈非常标准的一元一次函数,由于硬件不可抗力和电路本身存在的误差导致结果仍然无法较好拟合。

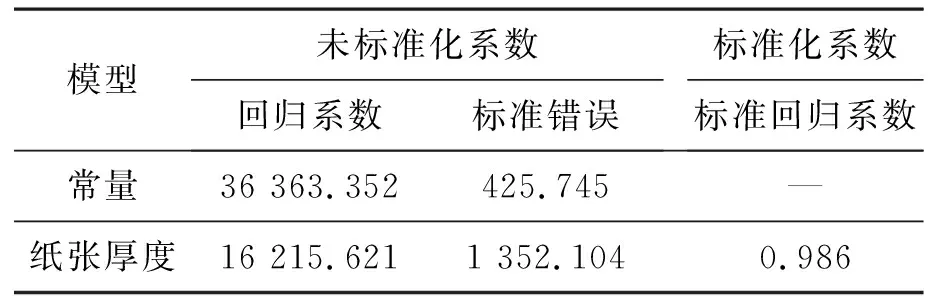
表6 0～5张纸拟合曲线系数

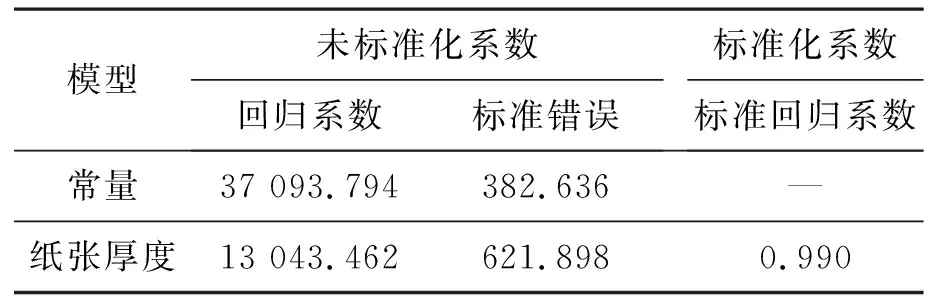
表7 6～10张纸拟合曲线系数

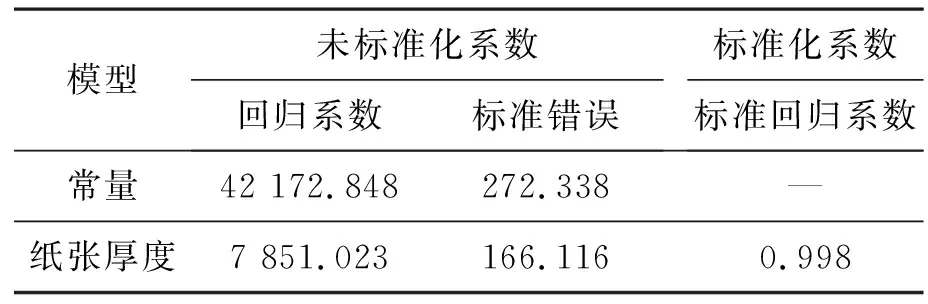
表8 11～20张纸拟合曲线系数

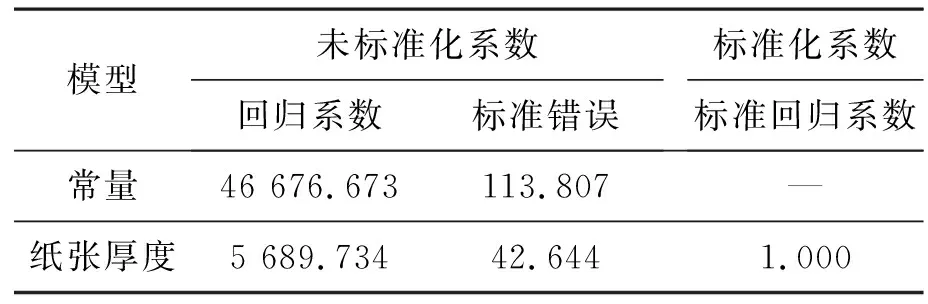
表9 21～30张纸拟合曲线系数

4 结 论

设计了一款基于单片机的纸张计数显示装置,打破传统的纸张计数方式,有效地解决了计数不高效和适用性不强的问题。本系统使用SN74LVC2G17DBVR型号的施密特触发器及使用卡尔曼滤波算法对装置分别进行方波整形及系统优化设计,通过取字模软件实现在OLED显示屏上显示文字的功能。利用串口接收数据并通过上位机观测频率波形、使用SPSS软件对纸张厚度d与频率f进行线性拟合,验证了本研究的可行性。在对0～30张纸张频率进行测量并发现拟合效果不好后,对测量方法进行了优化改进,采用分段拟合的方式对0～5张、6～10张、11～20张、21～30张纸张频率进行测量。经多次测试,得出本设计方案对1～10张变化的纸张数目测量正确率较高,测量精度为80%,10～30张纸张的测量结果正确率较低,测量精度为20%。