基于分数群稀疏混合范式和空间正则化的高光谱解混

王 伞, 王立国, 王丽凤

(哈尔滨工程大学 信息与通信工程学院, 哈尔滨 150001)

0 引 言

高光谱遥感技术广泛应用于环境监测、精准农业、林业监测和矿产勘探等领域[1]。由于成像传感器的空间分辨率有限,观察到的像元常由多种类型的地物组成,这种像元称为混合像元。高光谱解混合旨在估计混合像元中的纯光谱信号(端元)和相应比例(丰度)[2]。在高光谱解混研究中应用最广泛的光谱混合模型为线性混合模型(Linear sectral mixing model, LSMM),其中混合像元的反射率等于其相应的丰度和端元线性加权组合。利用LSMM,基于几何、统计和稀疏的高光谱解混方法逐步发展起来[3]。随着美国地质调查局(United States Geological Survey, USGS)光谱库的广泛使用,基于稀疏的高光谱解混方法已成为研究热点。高光谱稀疏解混方法旨在找到一个光谱库的最佳子集对高光谱图像的混合像元进行建模[4]。文献[5]首次采用l1范式来诱导丰度的稀疏性,提出了基于变量分裂和增广拉格朗日的稀疏解混算法(Sparse unmixing by variable splitting and augmented Lagrangian, SUnSAL)。为了结合空间信息,文献[6]将全变分(Total variation, TV)正则项引入SUnSAL,提出了SUnSAL-TV算法。TV正则化揭示了空间均质性,即两个相邻像元中含有同类端元的丰度相似。文献[7]通过将TV正则化和加权非局部低秩张量正则化引入到协作稀疏变分增广拉格朗日解混方法[8](Collaborative SUnSAL, CLSUnSAL),提出了一种加权非局部低秩张量稀疏解混方法(Weighted nonlocal low-rank tensor decomposition method for sparse unmixing, WNLTDSU),同时利用了局部空间平滑性、全局稀疏性和非局部低阶性。SUnSAL-TV、CLSUnSAL和WNLTDSU假设一个端元代表一种类型的材料,忽略了端元光谱可变性。解决这个问题的一个更为理想的方法是引入群稀疏性;即光谱库被组织成多个端元群,每个端元群代表一种类型的地物。解混时,混合像元中只有少数端元处于活跃状态;因此,估计的丰度是稀疏的,并且具有群结构。文献[9]提出了三种群稀疏混合范式lG,2,1、lG,1,2和lG,1,q。lG,2,1范式称为Group Lasso(G-Lasso),它诱导少数丰度群是活跃的,而这些活跃丰度群中的大部分丰度都是活跃的。lG,1,2范式称为Elitist Lasso(E-Lasso),它诱导多数丰度群活跃,而这些活跃的丰度群体中少数丰度是活跃的[9]。lG,1,q范式称为Fractional Lasso(F-Lasso),它诱导少数丰度群和每个群中的少数丰度活跃[9]。当端元和端元群的数量较大时(即场景中有多种类型的地物),lG,1,q范式的性能优于lG,2,1和lG,1,2范式。群稀疏混合范式针对具有群结构的光谱库进行丰度稀疏诱导,获得的丰度具有群结构,即每个端元群包含的多端元均参与解混并具有对应丰度,群稀疏混合范式能较好地将端元光谱可变性纳入解混模型;但群稀疏混合范式没有考虑丰度空间均质性特征对丰度的约束,导致估计的丰度欠平滑,因而将TV正则化引入到群稀疏解混,有助于提高丰度估计精度。

本文将TV空间正则化引入到分数混合范式lG,1,q中,提出了一种基于图像的光谱库提取、分数群稀疏混合范数和TV空间正则化的高光谱解混算法(Hyperspectral unmixing algorithm based on image spectral library extraction, fractional group sparse mixing norm, and TV space regularization, HU-ISLE-FTV)。采用一种新的基于图像的光谱库提取方法,称为基于顶点分量分析(Vertex component analysis, VCA)和概率输出支持向量机(Probabilistic outputs support vector machine, PSVM)的自动光谱库提取算法(Automatic spectral library extraction algorithm based on VCA and PSVM, ASLE-VPSVM)。传统稀疏解混方法利用通用光谱库解混,容易产生光谱库与待解混数据失配问题,同时,通用光谱库中通常利用单个端元光谱代表一类地物,未能很好地体现端元光谱可变性。ASLE-VPSVM针对待解混数据提取端元,克服了稀疏解混算法对通用光谱库的依赖性,提高了它们的适用性。同时,ASLE-VPSVM提取多个端元代表一类地物,充分反映了客观存在端元光谱可变性,能够提高稀疏解混方法的解混性能。此外,ASLE-VPSVM可以用作无监督或半监督方法。传统稀疏解混算法注重丰度稀疏性诱导,忽略了丰度空间均质性,即两个相邻像元中含有的同类端元的丰度是相似的。HU-ISLE-FTV算法首先应用ASLE-VPSVM提取多端元作为光谱库,然后将TV空间正则化引入到F-Lasso混合范式中,在强化稀疏诱导的同时,施加丰度空间均质性约束,有效地提高丰度估计精度。同时,为HU-ISLE-FTV算法设计了一种高效简洁的交替方向乘子迭代法(Alternating direction method of multipliers, ADMM)[10],提高了算法运算效率。

1 相关工作

1.1 ASLE-VPSVM算法

以提取3类端元为例表示ASLE-VPSVM算法原理,如图1所示。ASLE-VPSVM算法首先从原始高光谱图像中随机选择像元构成随机图像子集,然后在该子集运用VCA算法[11]提取端元m1、m2和m3,并利用PSVM[12]判断提取端元(概率值为1)的邻域像元的概率估计值,该估计值体现了端元邻域像元归属于端元对应所属类别的可能性,概率估计值越大,则端元邻域像元为同类端元的可能性越大。ASLE-VPSVM方法在针对每个随机图像子集提取端元时,包含2次提取过程,过程1利用VCA提取端元,过程2利用PSVM判断过程1中已提取端元的邻域像元是否为同类端元,如符合条件,则提取为端元。可见,ASLE-VPSVM既充分利用了光谱特征空间,即采用VCA方法,同时充分利用空间信息,即利用PSVM判断端元空间邻域像元为端元的可能性。

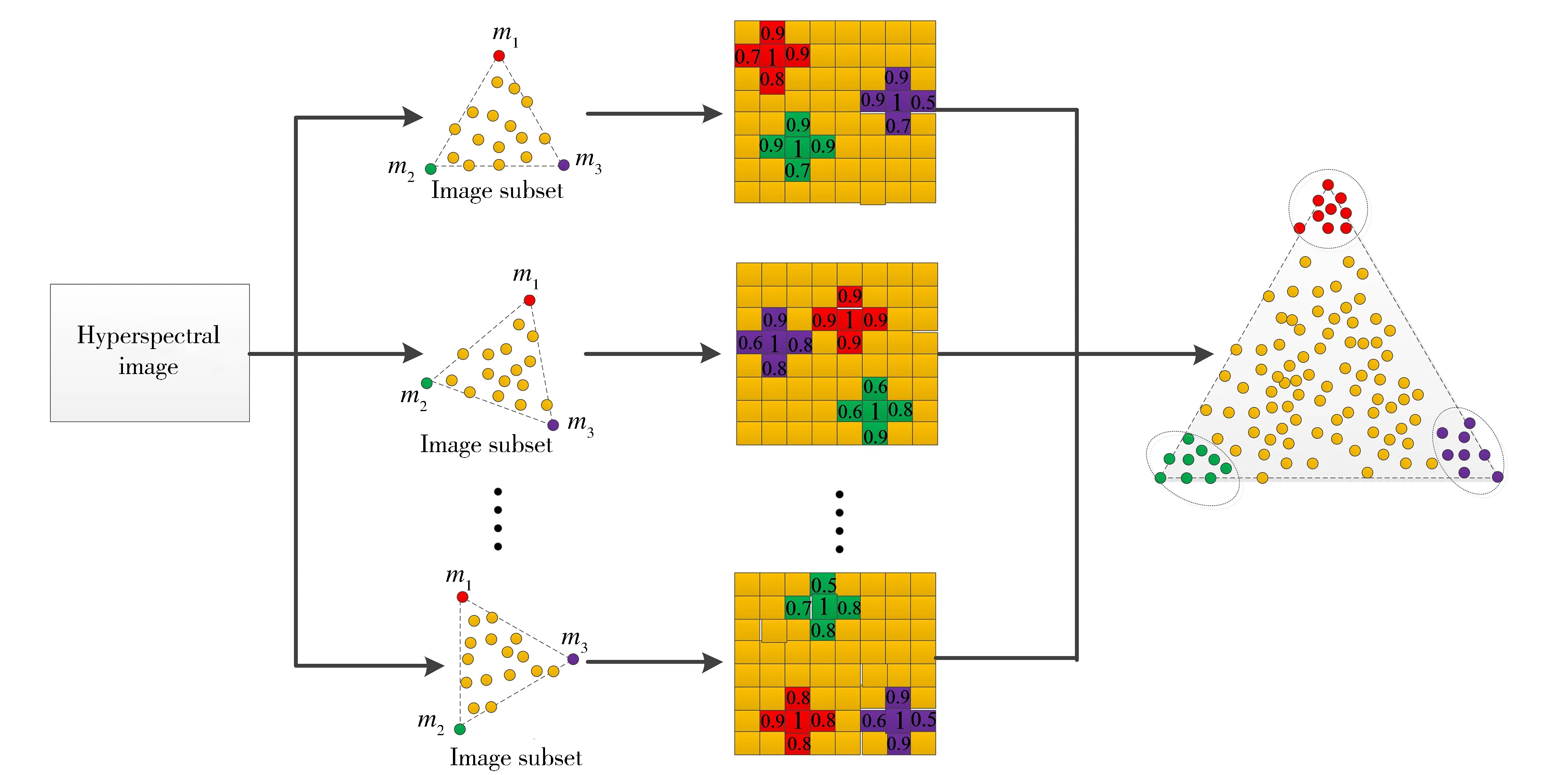
图1 ASLE-VPSVM算法原理图

ASLE-VPSVM算法具体实现过程如下:

步骤1: 从原始高光谱图像中随机选择一定比例的像元构成图像子集。在该图像子集中,运用VCA算法提取P个端元及其位置索引。P为原始高光谱图像中存在的端元类别数量,端元的位置索引是指其在原始图像中的位置坐标。

步骤2: 根据步骤1中提取的端元位置索引找到提取的P个端元的空间邻域像元(采用4邻域像元)作为候选端元。将已提取端元用作训练集,使用PSVM算法[12]预测候选端元概率。当候选端元的概率值大于阈值时,将其提取为真实端成员并添加到已提取端元。已提取端元是由步骤1和步骤2中提取的端元构成。

步骤3: 重复步骤1和2若干次后终止迭代。然后,从提取端元集合中移除冗余样本,最终获得光谱库。ASLE-VPSVM可用作无监督方法或半监督方法。当ASLE-VPSVM用作无监督方法时,在步骤1中,应首先应用HySime算法[13]估计端元种类数量P,并通过VCA提取端元。然后将已提取端元的平均向量用作参考向量,通过计算光谱角度距离区分新提取的P端元属于哪一类端元。无监督ASLE-VPSVM可以区分端员类别,但不知道每种端元类别的具体属性。在通常情况下,P和参考向量已知,ASLE-VPSVM则可用作半监督方法。

1.2 HU-ISLE-FTV算法

令Y∈L×N代表一个具有L个光谱波段且包含N个像元的高光谱图像数据,M∈L×n代表一个具有群结构且包含n个端元的端元光谱库;A∈n×N代表丰度矩阵,其中每一列对应Y中一个像元的丰度向量a;则线性光谱混合模型可表述为:

Y=MA

(1)

当M由ASLE-VPSVM算法获得后,利用F-LASSO建立稀疏解混优化问题如下:

(2)

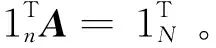
lG,1,q可以被视为l1和lq的一种“组合”。如图2(a)所示,群结构被定义为丰度向量的P个子向量, 图2(a)中每个黑框对应一个丰度子向量,每个子向量内的丰度构成一个丰度群,群中绿色、蓝色、红色和黄色代表数值不为0的丰度,其余淡色代表数值为0的丰度。lG,1,q首先计算每个子向量的l1范式以获得P维向量,然后计算该P维向量的lq范式以获得最终结果。在丰度非负的约束条件下,计算每个子向量的l1范式相当于计算子向量中所有丰度的总和。如图2(b)所示,lG,1,q范式可以很容易地扩展到丰度矩阵,按列计算l1范式并对结果计算lq范式。不失一般性,假设a为某一像元对应的丰度向量,则:

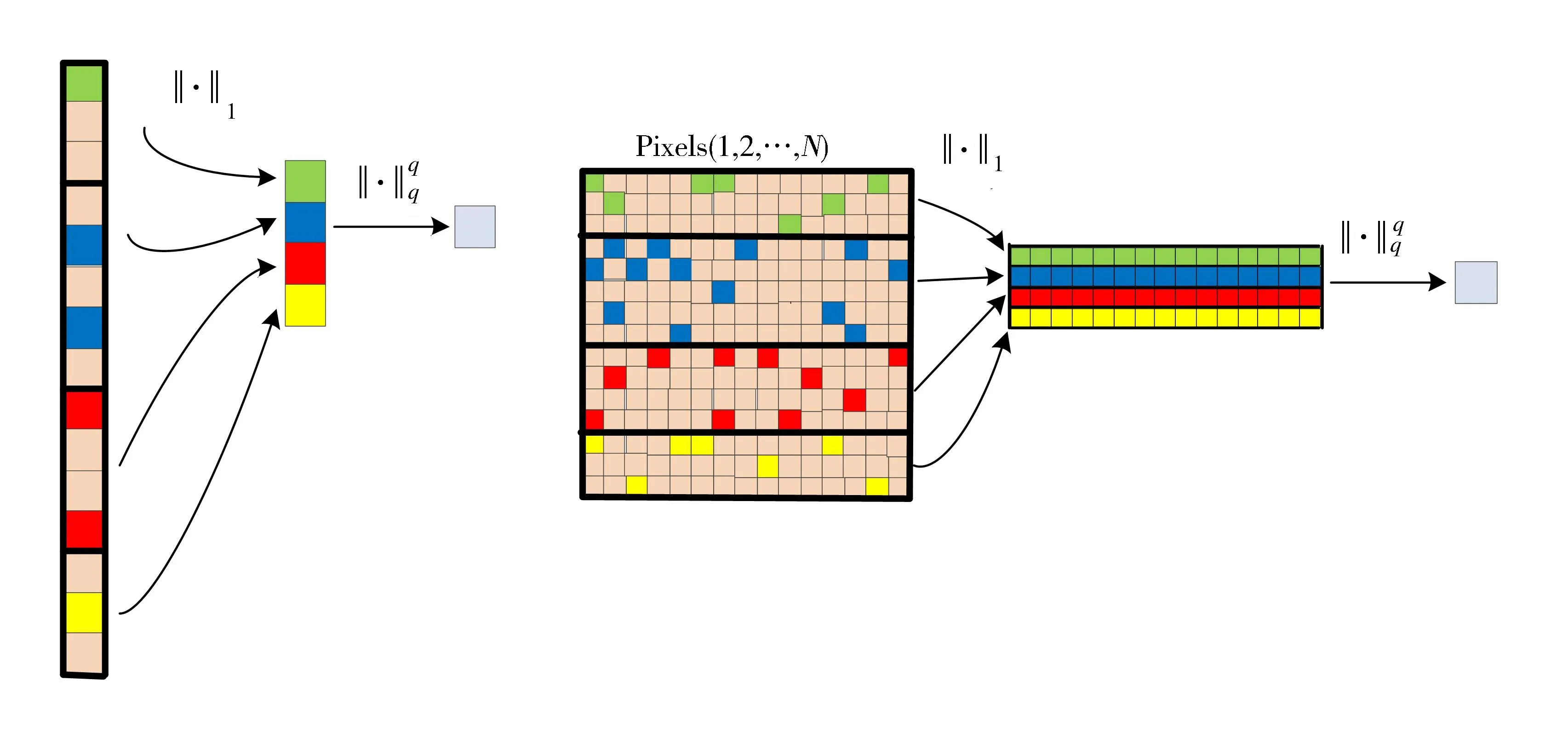
(a) lG,1,q作用于丰度向量 (b) lG,1,q作用于丰度矩阵

a=[a1,1,a1,2,…,a1,m1,a2,1,a2,2,…,a2,m2,…,aP,1,aP,2,…,aP,mP]T

(3)

由于a内每一个丰度都非负,那么求解a的lG,1,q范式相当于a的每个群内丰度相加得到一个P维向量,然后再求这个P维向量的lq范式。若定义G∈P×n为:

(4)

式中:第g行包含mg个连续的1,mg为第g个群包含丰度个数,那么式(3)等价为:

(5)

将TV正则化约束引入到F-LASSO解混模型,得到基于分数混合范式和总变分约束的解混模型如下:

(6)

定义Hh为一个线性算子,Hh:P×N表示计算当前像元与其空间垂直邻域像元的丰度向量之差,如Hh(GA)=[d1,d2,…,dN],式中di=ai-aih,i和ih分别表示某一像元及其垂直邻域。同样,定义Hν为一个线性算子,Hν:P×N表示计算当前像元与其空间水平邻域像元的丰度向量之差,如Hν(GA)=[d1,d2,…,dN],式中di=ai-aiν,i和iν分别表示某一像元及其水平邻域。

根据上述两个线性算子进一步定义:

(7)

根据分数混合范式和TV正则定义,式(6)的等效优化问题如下:

(8)

利用变量分裂的方法给出式(8)的约束等价公式:

(9)

式(9)的增广拉格朗日方程为:

(10)

利用ADMM将式(10)的优化过程分解为若干个简化的子问题进行求解。

(1) 变量A的优化子问题如下:

(11)

令式(11)中的优化目标函数对A求导并等于0,可得:

A←(MTM+2μGTG+μI)-1 (MTY+μGT(V1+D1+V2+D2)+μ(V4+D4))

(12)

(2) 变量V1的优化子问题如下:

(13)

参考文献[9]解式(13),可得:

V1←Sq,τ(GA-D1)

(14)

(3) 变量V2的优化子问题如下:

(15)

令式(15)中的优化目标函数对V2求导并等于0,可得:

V2←(HTH+I)-1(GA-D2+HT(V3+D3))

(16)

(4) 变量V3的优化子问题如下:

(17)

应用矢量软阈值[9]求解式(17),可得:

V3←Softτ(HV2-D3)

(18)

(5) 变量V4的优化子问题如下:

(19)

根据文献[16]解式(19),可得:

V4←projΔ(A-D4)

(20)

(6) 更新拉格朗日乘子D:

(21)

综上分析,总结HU-ISLE-FTV算法的ADMM如下:

步骤1: 输入高光谱图像数据Y,应用ASLE-VPSVM提取端元光谱库M;

步骤2: 利用全约束最小二乘解混方法(Fully constrained least square method, FCLSM)获得初始化丰度矩阵A,并进一步利用式(9)中约束条件计算初始化V;同时初始化D=0;

步骤3: 利用式(12)更新A;

步骤4: 利用式(14)、式(16)、式(18)和式(20)分别更新V1、V2、V3和V4;

步骤5: 用式(21)更新D1、D2、D3和D4;

步骤6: 循环执行步骤3至步骤5,直到满足迭代停止条件。

2 实验结果与分析

2.1 实验设置

2.1.1 实验数据

采用一个人工模拟数据集(DC1)和一个真实高光谱数据集Houston进行实验。模拟数据集DC1采用线性混合模型,由3类真实光谱和3个模拟丰度图人工线性合成而得到。3类真实光谱选自于USGS数字光谱库,分别为赤铁矿(Hematite)、白云母(Muscovite)和橄榄石(Olivine),上述光谱包含224个波段,均匀分布在0.4～2.5 μm。三类光谱分别包含12、13和17个端元,这样选取端元的目的是真实模拟高光谱数据的端元光谱可变性。模拟丰度图依据文献[6]中的方法生成,如图3第一列所示。每次从3类真实光谱中各随机抽取一个端元并结合丰度图中每个像元对应丰度,线性合成混合像元,最终得到63×63×224模拟数据集DC1。真实高光谱数据集Houston为2012年6月在美国德克萨斯州休斯顿大学校园拍摄的图像的子集,该图像包含区间0.380～1.050 μm的144个波段,具有2.5 m的空间分辨率。截取原数据集的105×128×144子集命名为Houston,该数据集包含4类不同地物:植被(Vegetation)、红色屋顶(Red roofs)、混凝土(Concrete)和沥青(Asphalt)。

图3 7种算法估计DC1数据中3类端元丰度图

2.1.2 实验算法及参数设置方法

参与实验的算法有FCLSU、SUnSAL-TV、G-LASSO、E-LASSO、F-LASSO、WNLTDSU和HU-ISLE-FTV等7种算法。其中,G-LASSO和E-LASSO需要设置的参数为μ和λ;SUnSAL-TV和WNLTDSU需要设置的参数为μ、λ和λTV;F-LASSO需要设置的参数为μ、λ和q;GSME-FTV需要设置的参数为μ、λ、λTV和q。μ设置为固定值0.05,λ和λTV在以下数值中进行取值:{10-5,5×10-4,10-3,5×10-3,0.01,0.05,0.1,0.3,0.5,1.00}。q在3个数值范围内取值,分别为0.001～0.01、0.01～0.1、0.1～1;每个数值区间包含10个等间距数值。上述参数遍历所有组合,可寻找最优参数。

2.1.3 实验结果评估指标

实验采用均方根误差(Root mean square error, RMSE)、光谱角距离(Spectral angular distanceroot, SAD)和重构误差(Reconstruction error, RE)作为量化指标评估解混结果,具体计算方式如下:

(22)

2.2 DC1数据实验

参与比较的7种算法利用ASLE-VPSVM所提取的相同光谱库进行解混。针对DC1数据,本实验运行ASLE-VPSVM 60次迭代,获得8个赤铁矿端元、9个白云母端元和7个橄榄石端元。图3显示了7种算法解混获得的丰度图,各种方法的量化评估结果如表1所示。图3中每一行对应一类端元,由上至下分别对应赤铁矿、白云母和橄榄石;每一列对应一种算法,由左至右分别对应真实丰度、FCLS、SUnSAL-TV、G-LASSO、E-LASSO、F-LASSO、WNLTDSU和HU-ISLE-FTV。由图3可以看出,与真实丰度图相比,7种方法估计的丰度图均不同程度包含噪声点,这是因为DC1中每个像元由3个随机选择的端元线性合成;端元光谱可变性很大,这影响了各种方法的解混性能。然而,7种算法均获得了较为清晰的丰度图,这是因为实验使用的ASLE-VPSVM提取的光谱库具有群结构,即每种类型的材料都由多个端元代表,可以更好地反映端元光谱可变性,从而验证了所提出的ASLE-VPSVM的有效性。图3显示,FCLSU和WNLTDSU估算的丰度图比其他五种方法估算的丰度图更为模糊,尤其是赤铁矿和橄榄石丰度图。SUnSAL-TV、G-Lasso、E-Lasso和F-Lasso估算的丰度图相似。与其他方法估计的丰度图相比,HU-ISLE-FTV估算的丰度图与真实丰度图更为吻合。表1表明,HU-ILSE-FTV在RMSE、RE和运行时间方面均优于其他算法,但SAM略大于其它大部分算法,HU-ISLE-FTV的运行时间明显短于其他稀疏解混算法,证实HU-ISLE-FTV设计的ADMM效率比较高。综上所述,HU-ISLE-FTV解混合成数据的性能优于其他参与比较的算法。

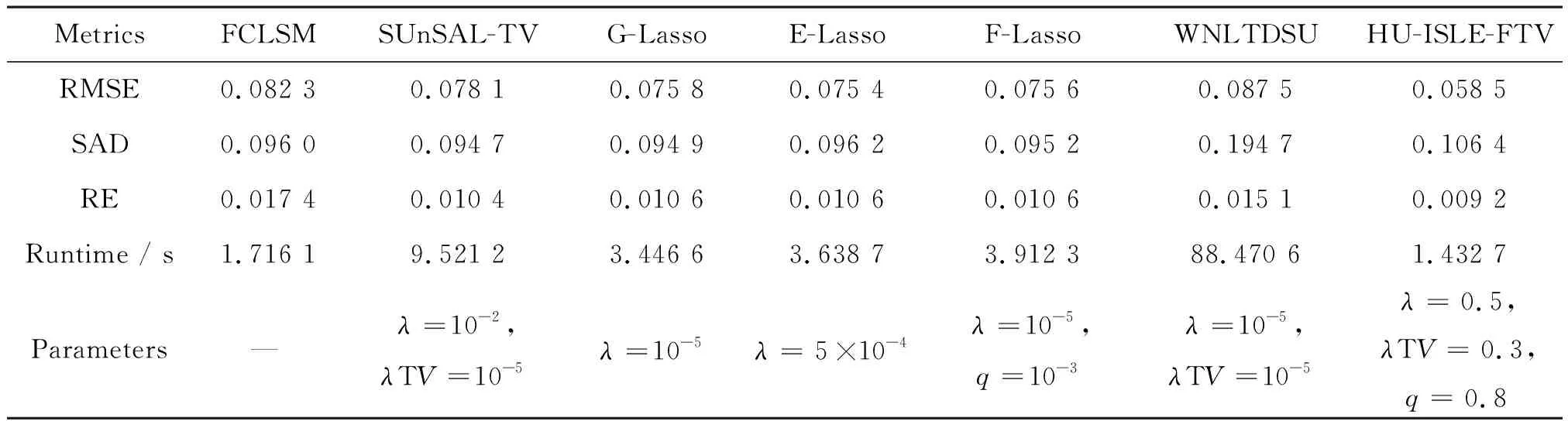
表1 7种算法解混DC1数据量化评估结果

2.3 Hunston数据实验

针对Hunston数据,运行了ASLE-VPSVM 60次迭代,获得15个植被端元、23个红色屋顶端元、21个混凝土端元和19个沥青端元。7种算法估计的丰度图如图4所示,表2列出了各种方法的量化评估结果。图中每一行对应一类端元,由上至下分别对应植被、红色屋顶、混凝土和沥青;每一列对应一种算法,由左至右分别对应FCLSM、SUnSAL-TV、G-LASSO、E-LASSO、F-LASSO、WNLTDSU和HU-ISLE-FTV。从视觉上看,几乎所有丰度图都清楚地显示了各类端元的分布。这验证了ASLE-VPSVM提取的光谱库能够很好地反映端元光谱可变性,验证了HU-ISLE-FTV算法的有效性。定量评估结果如表2所示,对于真实高光谱数据,由于无法获得其真实的丰度和端元,因此使用RE和运行时间作为评估指标。在所有方法中,HU-ISLE-FTV的RE最小,HU-ISLE-FTV的运行时间略高于FCLSU,远低于其他方法。综上所述,HU-ISLE-FTV解混真实数据的性能优于其他参与比较的算法。

表2 7种算法解混Hunston数据量化评估结果

3 结 论

提出了HU-ISLE-FTV算法,该算法设计了一种基于VCA和PSVM的自动光谱库提取方式,称为ASLE-VPSVM。ASLE-VPSVM提取多个端元代表一类地物,较好地解决了端元光谱可变性对高光谱解混的影响,并使稀疏解混算法不再依赖于通用光谱库。HU-ISLE-FTV将TV空间正则化引入分数群稀疏混合范数,在强化丰度稀疏诱导的同时施加空间均质性约束,有效地提升了丰度估计精度。对人工模拟数据集和真实数据集进行实验,结果表明HU-ISLE-FTV性能优于现有的6种代表性稀疏解混算法。未来的研究,将集中于将所提出的方法应用于非线性解混模型。