科技创新效率的时空格局、区域差异及收敛特征

马建辉，范谋远，何 淼，刘 煜

（1.河北大学a.经济学院；b.资源利用与环境保护研究中心，河北 保定 071002；2.天津大学 管理与经济学部，天津 300072；3.吉林大学 东北亚学院，长春 130012；4.中国政法大学 商学院，北京 100088）

0 引言

随着我国经济发展进入新常态，高质量发展成为时代主题。科技创新是推动高质量发展的原动力，依靠科技创新优化产业结构、完善产业链是实现国内国际双循环的关键。目前，我国科技创新发展呈现区域不平衡态势[1]，科技创新效率从投入、产出两个维度全面反映科技创新水平，科技创新效率的区域差异既是区域经济发展不平衡的体现，也是区域经济发展不平衡的原因[2]。因此，从空间格局、区域差异、收敛特征等角度研究我国科技创新效率，对于优化我国科技创新空间布局体系、推进区域科技创新水平协调、提升区域均衡协调发展水平、实现高质量发展、形成“双循环”新发展格局具有重大意义。

科技创新效率是科技创新投入转化为科技创新成果的一种量化指标，其从科技创新投入（成本）和产出（效益）两个维度全面表现区域科技创新能力和水平，是反映区域配置和运营科技创新资源能力的重要指标。学界目前对于科技创新效率的评价，主要是利用数据包络分析法（DEA）。传统DEA模型以规模报酬是否可变的前提假定为依据，可分为CCR 和BCC 模型[3]，这两类模型均为径向模型，即要求投入产出等比例变化，常常与实际情况不符。基于此，Tone（2001,2002）[4,5]提出了超效率SBM模型，它对投入产出同比变化进行了改进，同时又考虑了松弛变量问题[4]，并突破了效率值最大为1的局限，可以对前沿面评价单元进行更有效的评价[6]，故近年来采用此方法对科技创新效率进行测度的研究不断涌现[7,8]。基于区域均衡的视角对我国科技创新效率的研究，目前学界主要从时空格局[9]、区域差异[10]和收敛特征[11,12]三个维度展开。

已有研究取得了丰富的成果，为本文奠定了一定的理论和方法基础，但仍有进一步深入研究的空间。第一，对于时空格局表达方式单一，较少基于空间自相关的时空跃迁[6,13]等分析方法表达空间集聚状态的相互转化情况；第二，科技创新效率的评价多以省域为评价单元开展，以城市为评价单元的相关研究只存在于局部区域；第三，实施区域重大战略是实现高质量发展的重要支撑，以国家重大战略区域为重点研究对象，探讨科技创新效率的时空差异的研究在数量和质量上均有待进一步深入，且研究区域较少覆盖在区域发展战略中也较为重要的东北地区。

综上，本文以国家重大战略区域及东北地区为研究对象，以城市为基本评价单元，采用超效率SBM模型评价城市科技创新效率，基于地理分布图和空间自相关时空跃迁模型分析其时空格局，运用Dagum基尼系数研究其区域差异，并通过面板空间计量模型探讨其收敛特征，在完善科技创新效率时空演进研究体系、深化研究深度等方面具有一定的边际贡献，也可为差异化的科技创新管理政策的制定提供支撑。

1 研究设计

1.1 研究区域

参考王少剑等（2022）[6]、杨骞等（2021）[11]、张卓群等（2022）[14]、唐庆祥（2017）[15]的研究，本文以京津冀城市群、成渝城市群、长江中游城市群、长三角城市群、粤港澳大湾区、黄河流域以及东北地区为研究区域。结合数据的可获得性，最终确定179个城市为科技创新效率评价单元。样本时间跨度为2003—2020年。

1.2 科技创新效率的测度方法

科技创新效率的测度采用超效率SBM 模型，此方法基于全局DEA数学统计方法对每一个DMU每期的效率进行测算，从而实现结果的跨期可比。模型设置如下：

其中，ρ为效率评价指标；xk和yk分别为决策单元的投入和产出向量，X和Y分别为投入和产出矩阵；i和r表示不同评价单元，s-和s+表示投入产出的松弛变量；λ为列向量。

1.3 时空跃迁分析方法

时空跃迁分析是基于不同时期的局部Moran’s I，通过跃迁转移概率矩阵来探究区域变量局部空间关联类型转移规律。参考文献[16,17]的思路，根据区域内各城市科技创新效率莫兰散点图逐年的分布变化情况，确定其时空跃迁的类型①本文参考Rey（2001）[16]的研究，将跃迁类型分为四种。其中，类型I表示自身稳定-邻域稳定；类型Ⅱ表示自身跃迁-邻域稳定；类型Ⅲ表示自身稳定-邻域跃迁；类型Ⅳ表示自身跃迁-邻域跃迁，包括观测城市自身跃迁方向与邻域一致的ⅣA型跃迁和观测城市自身跃迁方向与邻域相反的ⅣB型跃迁。。

其中，t代表年份，i和r表示不同城市，n为城市总数，Yt代表第t年科技创新效率的均值，Yti、Ytr分别表示第t年第i、r个城市的科技创新效率值；w为空间权重，本文采用Queen邻接权重。

1.4 区域差异分析方法

科技创新效率差异分析通过Dagum 基尼系数模型[18]展开，其优点在于其可以同时体现组间（Gjh）、组内（Gjj）和总体（G）基尼系数，分别见式（3）至式（5）。并且，可以将总体差异分解为组内差异（Gw）、组间差异（Gnb）、超变密度（Gt），分别见式（6）至式（8）。

其中，y为科技创新效率；n为城市总数；nj、nh分别为j、h区域的城市数Djh为j、h区域之间的相对影响力。有关此模型参数的详细计算过程可参考文献[12,14]。

1.5 收敛性分析方法

收敛性主要用来分析经济现象是否趋于某种稳定状态，也被广泛应用于各种效率属性的分析。随着科技创新体系的完善，科技创新效率也可能收敛于某一稳定状态。本文采用相对β收敛进行研究。相对β收敛指在考虑众多因素（控制变量）对科技创新效率的影响下，随着时间的推移，科技创新效率低的区域具有更高的增幅，从而可以“追赶”上科技创新效率高的区域，区域间的差距将逐渐变小，直至达到同样的稳态水平。其模型如式（9）所示。

其中，ETC代表科技创新效率，i代表城市群，t代表时间，Yi，t+1代表控制变量。β是收敛系数，当β为负值时表示地区科技创新效率收敛，当β为正值时则表示地区科技创新效率发散，收敛速度为v= -ln(1-|β|)/T。μi、ηt和εit分别为地区效应、时间效应和随机干扰项。

由于科技创新效率可能存在显著的空间相关特征，本文利用空间计量模型进行研究。空间计量模型种类众多，较为基本、常用的有空间滞后模型（SLM）、空间误差模型（SEM）和空间杜宾模型（SDM），三种空间相对β收敛模型如式（10）至式（12）所示，具体模型的选择见下文实证分析部分。

其中，ρ表示因变量空间滞后系数，反映了邻近城市科技创新效率增长率对本城市的影响；λ是空间误差系数，反映了随机干扰项中存在的空间效应；π 是自变量空间滞后系数，反映了邻近城市科技创新效率的影响；wir是空间权重，设定规则同时空跃迁分析方法。

1.6 变量设计

（1）科技创新投入、产出变量

参考杨骞等（2021）[11]、马玉林和马运鹏（2021）[12]的研究，结合城市尺度数据的可获得性，本文确定科技创新投入、产出指标如表1 所示。投入指标数据来源于《中国城市统计年鉴》，专利授权数来源于中国研究数据服务平台（CNRDS），城市创新指数来源于《中国城市和产业创新力报告》。部分缺失数据，根据研究的样本区域与时间跨度，采用回归拟合的方法补齐。

表1 科技创新效率评价指标体系

（2）收敛模型控制变量

本文参考马玉林和马运鹏（2021）[12]的研究，选取4 个控制变量，如表2所示。专利授权数来源于由中国研究数据服务平台（CNRDS），其余数据主要来源于《中国城市统计年鉴》，部分缺失数据采用插值法补齐。

表2 相对β 收敛模型的控制变量

2 实证分析

2.1 科技创新效率的测度结果

科技创新效率描述性统计分析结果显示各研究区域的科技创新效率均存在明显差异；全国及各研究区域年度均值整体呈先降后升趋势，如图1所示。

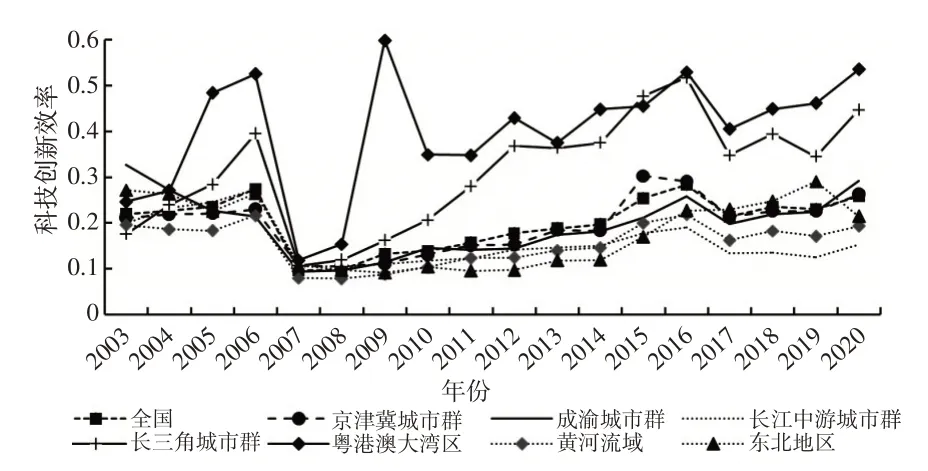
图1 全国及七个研究区域科技创新效率年度均值变化情况

2.2 时空格局及跃迁分析

2.2.1 时空格局分析

本文选取2003 年、2008 年、2014 年和2020 年作为样本年份，将城市科技创新效率的时空演变情况报告于图2。可以看出，科技创新效率整体呈先降后升的演变趋势，且高值区域从东北地区转移到东部沿海地区；科技创新效率较高的地区主要集中于长三角城市群和粤港澳大湾区以及北京、成都、哈尔滨等全国及区域中心城市。

图2 2003—2020年主要年份科技创新效率的时空演变

2.2.2 时空跃迁分析

基于全局Moran’s I 的空间自相关检验可知，在绝大部分时期，179个城市的科技创新效率整体上存在5%水平下显著的空间正相关性，说明各观测城市的科技创新效率会受到邻域的影响。从莫兰散点图可知，各城市之间科技创新效率的时空演进特征总体上呈现集聚（HH、LL）与分异（HL、LH）并存的状态，其中集聚略多于分异。

本文选取2003 年、2008 年、2014 年和2020 年为时间节点，根据莫兰散点图中各城市集聚类型的变化情况，总结2003—2008年、2008—2014年、2014—2020年三个阶段城市科技创新效率的时空跃迁转移矩阵，绘制堆积柱状图（见下页图3），并明确其时空变迁（SF）和时空凝聚（SC）特征①时空变迁为Ⅱ、Ⅲ类跃迁的占比，时空凝聚为I、ⅣA类跃迁的占比。。结果表明，三个时段内，各区域的跃迁形式以类型I、Ⅱ、Ⅲ为主，各区域科技创新效率发生跳跃转移的概率相对较低。其中，长三角城市群和粤港澳大湾区的I类跃迁占比不断上升，而Ⅱ、Ⅲ类跃迁占比不断下降，说明这两个区域的科技创新效率的转移惰性不断上升，局部时空关联类别间的转移特征不断弱化；全国、京津冀城市群、成渝城市群、长江中游城市群、黄河流域和东北地区的I 类跃迁占比的下降同步于Ⅱ、Ⅲ类跃迁总体的上升，即存在时空变迁指数的上升同步于时空凝聚指数的下降的现象，这说明这些区域科技创新效率空间格局的路径依赖和锁定特征逐渐减弱。

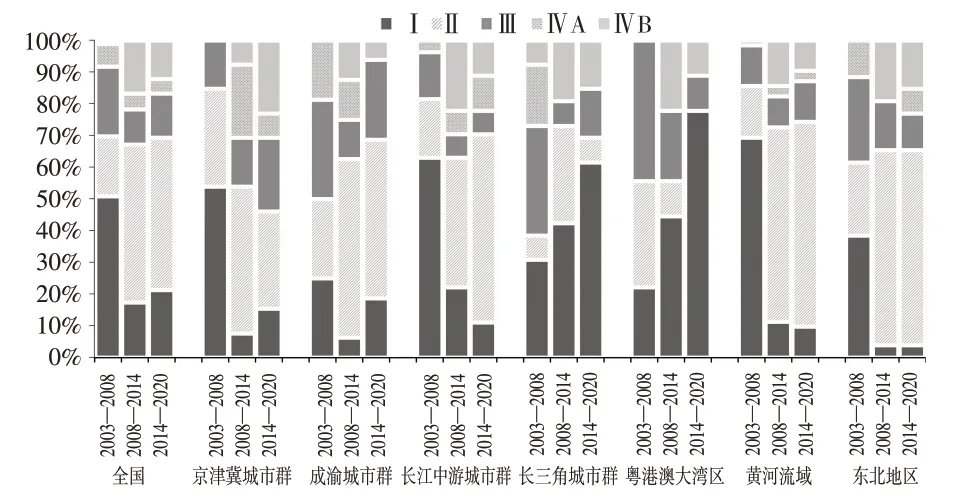
图3 全国及七个研究区域科技创新效率时空跃迁分组堆积柱状图

2.3 科技创新效率区域差异分析

2.3.1 组内组间科技创新效率差异

基于Dagum基尼系数，将全国和七个研究区域科技创新效率组内、组间差异的演变趋势分别报告于图4、图5。

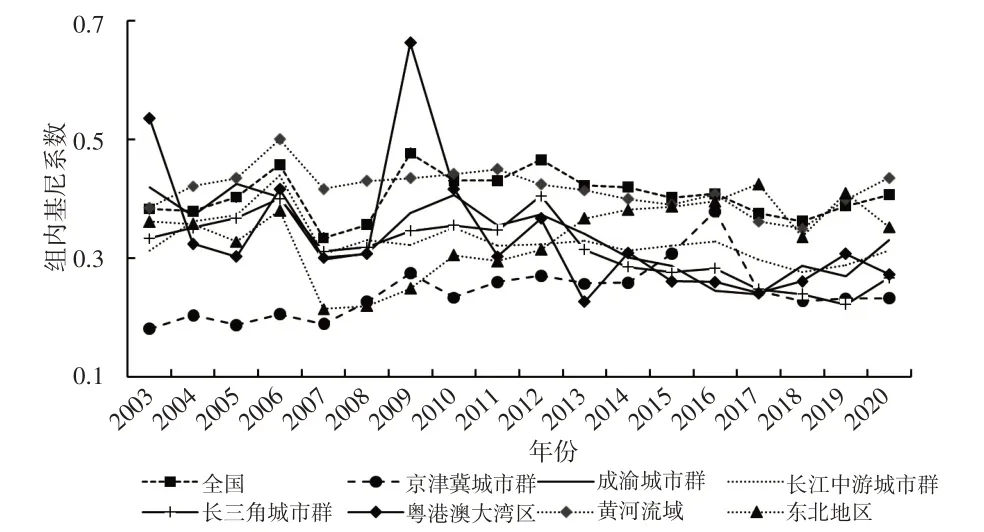
图4 科技创新效率组内差异的变化情况

图5 科技创新效率组间差异的变化情况

由图4可知，样本期内全国组内基尼系数呈现不规则小幅波动状态，均值为0.406，相对较高，说明各城市间科技创新效率存在着明显的不均衡现象。各研究区域内部差异程度也不相同，内部基尼系数大体介于0.2～0.5。其中，黄河流域的样本均值最高，在逐渐下降后略有回升，说明科技创新效率的区域差异在缩小，但不平衡不充分问题依然突出。其余城市群组内基尼系数均未超过全国的整体水平，粤港澳大湾区组内基尼系数波动较大，整体呈现下降趋势，东北地区组内基尼系数为波动上升趋势；成渝城市群基尼系数不断波动；长江中游城市群组内差异相对较小；长三角城市群基尼系数演变趋势整体呈现“M”型波动；京津冀城市群组内差异的均值最低，总体较为稳定。

由图5 可知，阴影部分的面积整体先变小再变大，这说明七个研究区域之间的科技创新效率的差异存在一个先减小后扩大的过程。就区域间基尼系数的样本均值而言，京津冀城市群和成渝城市群之间的基尼系数均值最低，粤港澳大湾区和其他研究区域之间的差异均较大；研究期内，组间的较大差异值均出现在2009 年粤港澳大湾区与其他研究区域之间，原因在于该年度粤港澳大湾区联合创新的策略对于科技发展产生了显著影响[19]。

2.3.2 科技创新效率的差异来源及其贡献率

图6显示，在2009年之前，超变密度的贡献率最大，组间差异的贡献率次之，组内差异的贡献率最小；在此阶段，超变密度的贡献率均值为54.60%，表明在此期间交叉重叠问题不是各研究区域之间科技创新效率存在差异的主要原因；2009 年之后，组间差异的贡献率陡增为55.13%，并在此后一直稳定于较高水平，相对而言，超变密度的贡献率从2009 年开始变小，组内差异的贡献率则依旧处于较低水平。总体来看，在全样本时期，尤其是在2009年之后，组间差异为影响科技创新效率整体差异的主要原因，这显然与各个研究区域的经济实力、实际利用外资额、国家政策、教育投入等多个方面的因素有关。

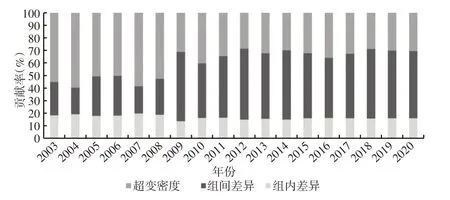
图6 科技创新效率的空间差异来源

2.4 科技创新效率收敛性分析

本文综合LR和Wald统计量，并结合LM检验，选择最优的空间模型形式进行相对β收敛分析。179 个城市和七个研究区域的相对β收敛结果见下页表3。

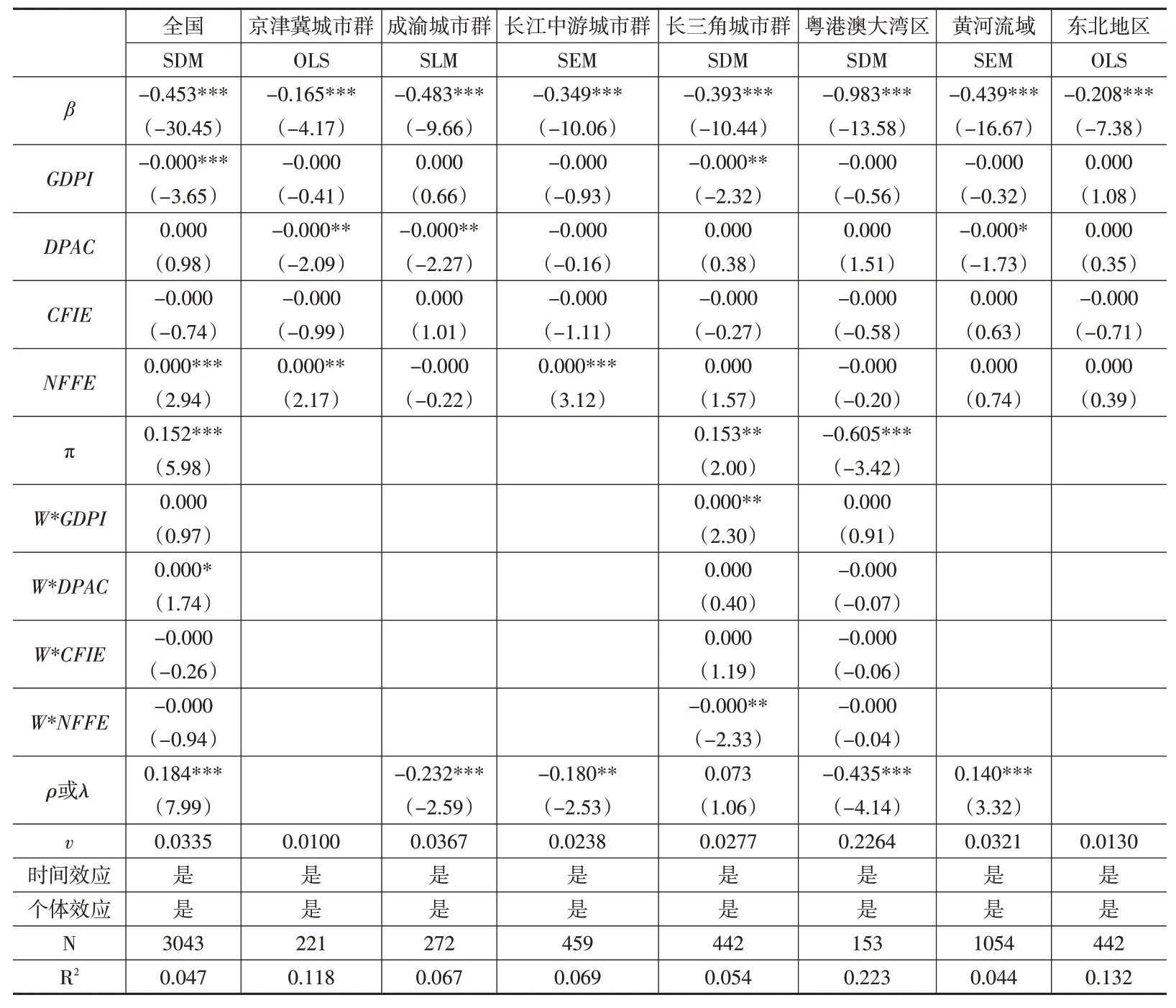
表3 全国及七个研究区域相对β 收敛检验结果

结果表明，第一，全国及各研究区域相对收敛系数β均在1%的水平下显著为负，这说明，在考虑经济发展水平、对外开放程度、科技创新水平、教育支持力度这些经济社会因素的影响的情况下，全国及七个研究区域的科技创新效率均会向各自的稳态水平收敛。第二，全国及七个研究区域各自的收敛速度存在差异，全国的收敛速度为0.0335，各研究区域中仅有粤港澳大湾区和成渝城市群高于全国平均水平。第三，全国及七个研究区域的空间效应存在异质性，其中，全国和粤港澳大湾区的被解释变量和解释变量均存在空间滞后效应，长三角城市群仅存在解释变量的空间滞后效应，成渝城市群仅存在被解释变量的空间滞后效应，表明上述研究区域的城市科技创新效率受到相邻城市空间溢出效应的影响；此外，长江中游城市群和黄河流域存在空间误差效应，京津冀城市群和东北地区不存在空间效应。

3 结论与启示

3.1 结论

（1）从时空格局及跃迁看，七个研究区域科技创新效率在样本期内呈现先下降后上升的趋势，高值区域从东北地区转移到东部沿海地区；科技创新效率较高的地区主要集中于长三角城市群和粤港澳大湾区以及北京、成都、哈尔滨等全国及区域中心城市；研究期内全国科技创新效率整体上存在正向溢出效应；除长三角城市群和粤港澳大湾区外，其余各研究区域的科技创新效率时空凝聚指数不断下降，时空变迁指数不断上升，说明其局部空间格局的路径依赖和锁定特征不断弱化。

（2）从区域差异来看，组间差异是科技创新效率的主要来源。组间差异中，南北研究区域间差异较大，反映出南北创新战略存在显著差异，不平衡问题突出。组内差异中，黄河流域科技创新效率组内差异相对较大，科技创新发展明显不均衡，这与区域内各城市资源禀赋差异较大有关；长江中游城市群、京津冀城市群组内差异相对较小，科技创新效率较为平均，科技发展水平较为均衡。

（3）从收敛特性来看，全国及七个研究区域均存在相对β收敛，其科技创新效率均存在收敛于各自稳态水平的趋势。各研究区域的空间效应呈现差异化特征，全国、长三角城市群、粤港澳大湾区和成渝城市群均存在不同形式的空间滞后效应，长江中游城市群和黄河流域存在空间误差效应，而京津冀城市群和东北地区不存在空间效应。

3.2 启示

（1）科技创新应注重协同发展。发展过程中，应考虑各地资源禀赋、经济发展阶段、社会条件等客观因素，在一定时期内正视差异的客观存在及其合理性。目前，我国科技创新效率差异主要在于组间差异，应充分发挥长三角城市群、粤港澳大湾区、京津冀城市群等高创新水平集群区域的辐射带动作用，如建立东西部科技合作示范区，做到既注重区域间的协调，又注重区域内创新产业结构的调整，全面加速科技创新发展进程。

（2）科技创新战略制定应因地制宜。各地区的科技创新效率均存在显著的收敛趋势，但强调缩小差距、协同发展并不意味着使各地区科技创新水平完全一致，而是在考虑各城市实际情况的基础上，在其各自的稳态水平上实现一种相对均衡。各个城市群结合科技创新发展布局，形成相应的科技创新发展路径，打造带有地域特色的创新高地，如可从教育资源、经济、地理条件等不同角度制定相应策略推动科技创新效率的提升。

（3）科技创新应以市场为先，注重创新要素流动。近年来，随着5G、人工智能的发展，科技创新人才、数据、资金等创新要素成为科技创新发展的关键要素，各区域通过优化创新机制促进要素流入，但区域创新体系仍存在要素或功能短板，结果使得创新回报率下降，影响创新体系整体作用的发挥。政府可因势利导，搭建科技创新平台，多渠道增加创新要素投入，如与企业进一步开展合作、给予科技创新人员股权等激励性收益。