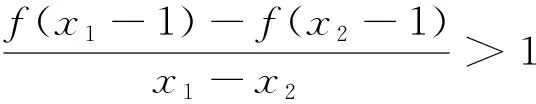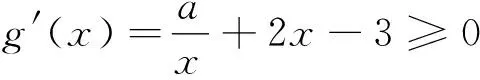例谈“同构法”在高中数学解题中的应用
江苏省南京市高淳区教师发展中心 (211300) 夏继平
同构法就是对函数、方程、不等式进行适当变形,使之成为结构一致,便于抽象出本质属性,进而解决相关问题的方法.在近几年高考题、模拟题中屡屡出现.因此,笔者试图从以下三个方面举例说明,以飨读者.
一.同构法在“ex,lnx”混合型函数中的应用
1.转化为“y=ex±x”型函数
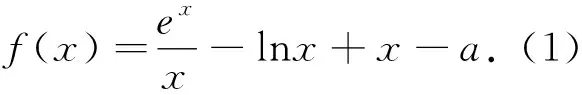
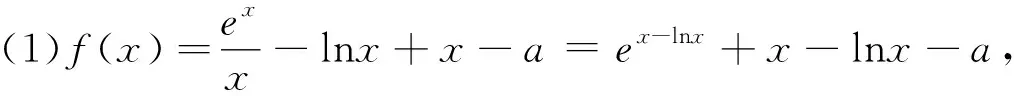

例2 (2021江苏高三模拟卷)已知函数f(x)=lnx-ax.(1)讨论f(x)的单调性;(2)设g(x)=ex-1+xf(x),若g(x)≥0,求a的取值范围.

2.转化为“y=x±lnx”、“y=xlnx”、“y=xex”型函数
例3 (2020山东卷)已知函数f(x)=aex-1-lnx+lna.(1)当a=e,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;(2)若f(x)≥1,求a的取值范围.
解:第(1)问略;
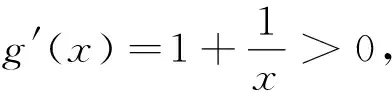
(法二)f(x)=aex-1-lnx+lna≥1可变为elna+x-1-lnx+lna≥1,即elna+x-1+lna+x-1≥lnx+x=elnx+lnx.设函数g(x)=ex+x,g′(x)=ex+1>0,所以g(x)在R上单调增,所以有lna+x-1≥lnx,即lna≥lnx-x+1,设h(x)=lnx-x+1,以求得h(x)最小值为0,所以有lna≥0,所以a的取值范围为[1,+∞).
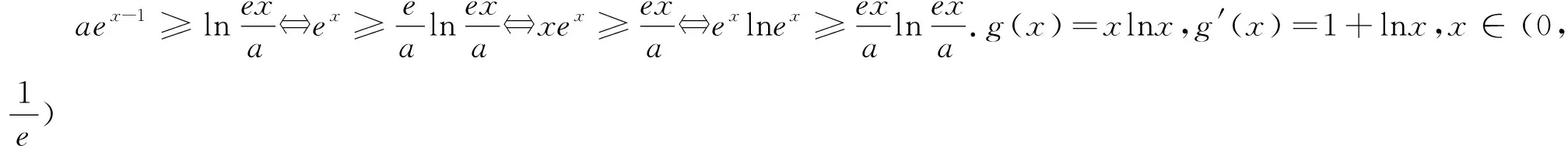
3.转化为“y=ax+logax”“y=ax+bx”型函数
例4 (2020全国Ⅰ理)若2a+ log2a = 4b+ 2log4b,则( ).
A.a>2bB.a<2bC.a>b2D.a 变式(2020全国2)若2x-2y<3-x-3-y,则( ). A. ln(y-x+1)>0 B. ln(y-x+1)<0 C. ln|x-y|>0 D. ln|x-y|<0 答案:A. 说明:对于同时含lnx、ex的函数求最值范围问题,或可转化为求最值的恒成立能成立的问题,可考虑使用同构法,其法运用的本质是将常数、字母、代数式转化指数式或对数式,即对数运算法则“a=lnea”,“a=elna”的一般化运用,只要熟练掌握代数式化指对的两种基本运算法则,同构lnx、ex混合型函数就可迎刃而解. 例5 (2022新高考Ⅰ卷) 已知函数f(x)=ex-ax和g(x)=ax-lnx有相同的最小值.(1)求a;(2)证明:存在直线y=b,其与两条曲线y=f(x)和y=g(x)共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列. 例6 (2021全国甲文2)抛物线C的顶点为坐标原点O.焦点在x轴上,直线l:x=1交C于P,Q两点,且OP⊥OQ.已知点M(2,0),且圆M与l相切.(1)求C圆M的方程;(2)设A1,A2,A3是C上的三个点,直线A1A2,A1A3均与圆M相切.判断直线A2A3与圆M的位置关系,并说明理由. 变式(2021全国乙理)已知抛物线C:x2=2py(p>0)的焦点为F,且F与圆M:x2+(y+4)2=1上点的距离的最小值为4.(1)求p;(2)若点P在M上,PA,PB是C的两条切线,A,B是切点,求△PAB面积的最大值. 说明:出现在解析几何中的同构方程,则可把x1,x2,y1,y2一般化,转化为关于x、y的方程来解决问题. A.[-9,+∞) B.[-7,+∞) C.[9,+∞) D.[7,+∞) 说明:在含抽象函数的方程或不等式中,常把含x1,x2的代数式分开移至两边,形成同构解决问题. 综上知,同构法作为一种代数变形技巧能提升学生解决问题的效率;同构作为一种教学方式能彰显教师的执教水平;同构作为解决问题的方法能体现数学美感及运算核心素养.
二.同构法在方程中的应用
1.“ex-x=elnx-lnx”,“x-lnx=ex-lnex”型同构

2.“Ax1+By1+c=0,Ax2+By2+c=0”型同构
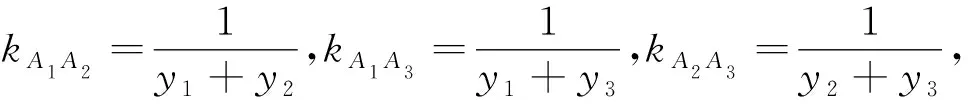
三.同构在抽象函数中的应用