例说高中数学解题教学思维变通的五种策略*

江苏省江浦高级中学 (211800) 徐爱勇

数学思维能力是数学能力的核心.教学实践中,教师应注重培养学生处理数学问题的自觉意识和思维习惯,发展学生的数学观念,着力提升学生的数学思维能力和解题水平.本文举例来谈如何在高中数学解题教学中开展思维变通的“由近到远”、“由数到形”、“由次到主”、“由低到高”、“由显到隐”等五种策略,希望能给读者些许启示.

1 由远到近

在解题过程中,有些问题从条件(“近处”)直接求解会遇到较多思维障碍,此时可以考虑改变思维的方向,逆向而行,即从结论(“远处”)着手,通过对结论的分析,执果索因,寻找解决问题途径.

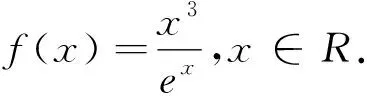
(1)求函数f(x)的单调区间与极值;

分析：可以从所求证的不等式出发,逐步寻求使不等式成立的充分条件,直至所需条件被确认成立,就断定求证的不等式成立,这种证明方法统称为“分析法”(“由远到近”法).

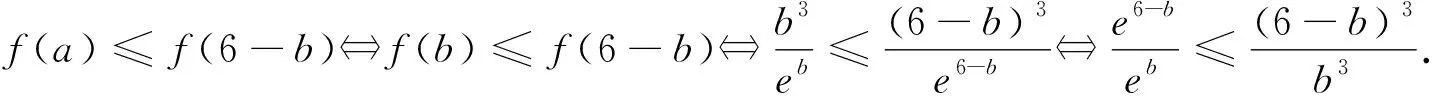
评注：不等式证明中常用的方法有“分析法”(“由远到近”)和“综合法”(“由近到远”).分析法与综合法是思维方向相反的两种思考方法.分析法是从待证的结论出发,一步一步地探索下去,最后到达题设的已知条件,即推理方向是:结论到已知.综合法则是从已知条件出发,经过逐步的逻辑推理,最后到达待证的结论,即推理方向是:已知到结论.

2 由数到形

例2 若存在x<0,使得不等式x2<2-|x-t|成立,则实数t的取值范围是．

分析：本题给我们的第一印象是“解不等式”.再做思辨,究竟如何解该不等式(“由数到形”或“由形到数”),均存在着解题策略的选择问题.

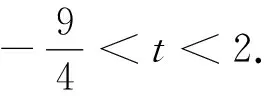
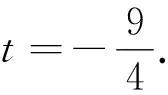
评注：数学解题中建立一些模式(如“数形结合”)必要且重要.本题可以建立“数形结合”模式、“等价转换”模式等.教学实践中,需指导学生在问题解决后,主动提炼出适合自己的一些模式,而不要把现成的模式抛给学生记忆.

合理的合同条款设置可以有效降低工程量清单风险。依据工程项目各分部工程要求，共有可调总价合同、固定总价合同、单价合同等几种类型。为了避免合同漏洞导致工程招标方规避工程价款索赔风险，可在合作协议签订期间，利用可调总价合同控制分部工程实际工程量与工程量清单中工程量差额在±5.0%以内，若工程量上升幅度在标准限度外，则需要依照综合单价的95%执行。

3 由次到主

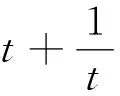
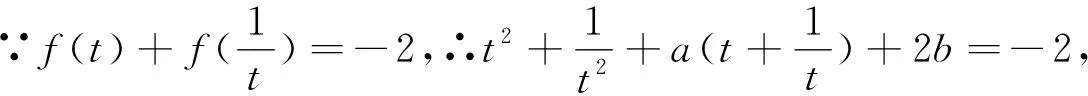
评注：“主次转换”是把未知解的问题转化到在已有知识范围内可解决问题的一种重要的思想方法.通过不断地转化,把不熟悉、不规范、复杂的问题转化为熟悉、规范甚至模式化、简单的问题.教学实践中,需培养学生自觉转化的意识,强化解决问题中的应变能力,提高思辨能力.在“主次转换”时要注意转化的等价性与非等价性的不同要求,实施转化时确保其等价性,保证逻辑上的正确.

4 由低到高

例4 “在Rt△ABC中,∠A=90°,AD⊥BC于点D,则AD2=BC·CD”.类比平面几何的这一性质,在立体几何中“在三棱锥A-BCD中,三条侧棱AB,AC,AD两两互相垂直,AE⊥平面BCD于点E,则．”

分析：平面几何和立体几何在研究对象和方法、构成图形的基本元素等方面是相同或相似的.因此,在两者之间进行类比是研究它们性质的一种非常有效地方法.回顾题干所给信息,可知等式AD2=BD·CD是由对应三角形相似得到的.而在立体图形中,我们可以将该平面构图作为一个基本单元,并进行“由低到高”(将边长类比为面积)转换,则对应结论可自然呈现.

评注：“由低到高”(类比)作为一种科学的研究方法,其作用早就被科学家们所认识到.开普勒曾说:“我珍视类比胜于任何别的东西,它是我最可信赖的老师,它能揭示自然界的秘密,在几何学中它应该是最不容忽视的”.

5 由显到隐

例5 在△ABC中,角A,B,C所对的边为a,b,c,且a,b,c成等差数列,若a2+b2+c2=84,则实数b的取值范围是．

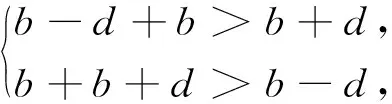
评注：数学问题难度的标志之一是隐含条件的深度与广度.一般来说,隐含条件通常隐蔽在数学定义与性质中;或者隐蔽在函数的定义域与值域之中;或者隐含在已知条件与未知结论分别进行顺推与逆推的过程中;或者隐蔽在几何图形的特殊位置上;或者隐蔽在知识的相互联系之中.若能深入挖掘题目中的隐含条件,并充分加以利用,常常可以使问题得到迅速而巧妙的解决.教师在平时的教学中,需引导学生挖掘数学问题中的隐含条件,使学生形成全面、深入地把握各种信息的能力,培养学生思维的深刻性.

以上五种解题思维策略,以其适用的广泛性而区别于解题的具体思路和方法.五种解题思维策略各注重方向、角度、主次、维度、显隐,并以此提高解题的灵活性和准确性,培养了学生思维的广阔性、深刻性.学生在日常的学习和高考复习中,学会运用这五种思维策略是必要的,同时在运用的过程中极大地激活了学生的多元思维,最终达到提升数学思维品质的目的,真正有助于自我能力的完善和升华.