一道模拟题的解法探究与背景探源*

重庆市长寿中学 (401220) 兰祥平 田 鹏

1.试题呈现

图1

(I)求椭圆C的方程;

(II)设椭圆的左右顶点分别为A,B,M是椭圆C上异于A,B的任一点,直线MF交椭圆C于另一点N,直线MB交直线x=4于点Q,求证:A,N,Q三点在同一条直线上.

2.解法探究

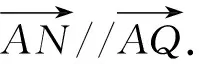
评注：证明三点共线的常用方法有向量法和斜率法,本质是将几何问题转化为代数问题.解法1将三点共线问题转化为向量共线问题,然后将向量问题转化为代数问题,体现了转化思想的应用.

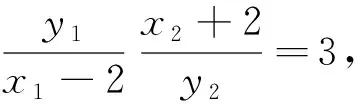
评注：解法3同样采用的是同一法,将直线MN的方程设成参数形式.

评注：解法4采用面积证法.要证三点共线,只需证明由这三点围成的三角形面积为0.由三角形三个顶点的坐标求三角形面积可采用行列式的方法.

评注：解法5利用椭圆的参数方程,设出点M和N的参数坐标,再利用M,F,N三点共线构建关系,再利用三角恒等变换化简证明.

3.试题推广

著名数学家波利亚说过:“好问题同某种蘑菇有些相似,它们大都成堆地生长,找到一个以后,你应当再在周围找一找,很可能在附近就有几个.”

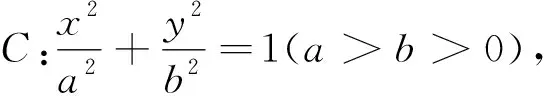
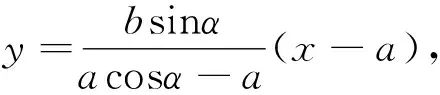
实际上,性质1只是问题的初步推广,站在高等几何的角度,该问题还可以进一步推广.首先从方程的角度给出二次曲线极点与极线的定义.

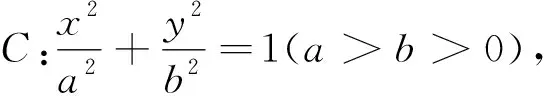
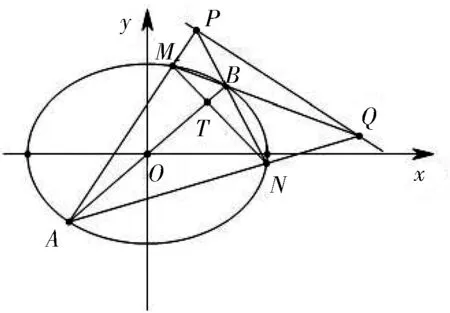
图2