一道解析几何试题的求解探究之旅*

广东省中山市烟洲中学 (528401) 周建刚

解析几何中涉及到的动点及相关的最值问题常常是高考和模拟考的热点和难点,是学生比较畏惧的题型之一,因其内涵丰富,解法灵活,备受命题者的青睐.本文对2022年南昌市一模第12题求解进行研究,从不同的角度给出四种解法,并对就其命制进行追根溯源.

1 试题呈现与分析

已知A(-1,0),B(3,0),点P是圆O:x2+y2=45上的一个动点,则sin∠APB的最大值为( ).

试题背景平和、内涵丰富,从知识层面看,主要考查圆的几何性质、圆上动点相关角的最值等知识;从能力层面看突出考查学生运算求解、思考探究、逻辑推理等方面的能力;试题的思维过程和运算思路凸显了能力立意的命题思想,较好地体现了对解析几何中综合函数、不等式、解三角形等核心内容和思想方法的考查,也能较好地检测学生的学习潜能和数学素养.

2 解法探究

思路1 几何问题代数化

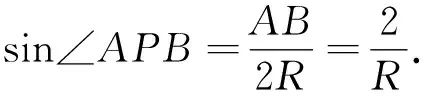
评注：先设点P坐标根据中垂线关系表示外接圆圆心M,再建立目标函数利用圆的参数方程,结合辅助角公式求最值,解题思路较为常规,但运算过程较复杂.

思路2 运用到角公式

评注：利用圆的参数方程设先设点P坐标,进而表示直线PA、PB的斜率,借助到角公式表示出∠APB的正切值,再利用辅助角公式求相应的最值,本解法对于学生而言好算但不好想,到角公式是教材之外的补充知识,学生接触的不多,需要强化和积累.

思路3 运用柯西不等式

评注：先根据圆的对称性利用三角形的面积建立关于∠APB的正切函数关系,再根据柯西不等式求最值,极大简化运算过程,简洁明了.

3 追根溯源 总结提升

湘教版普通高中课程标准试验教科书《数学(必修二)》第260页习题如下:

如图1,足球运动员在国际标准足球场上沿下列直线方向带球推进,试寻找最佳的射门位置,使得射门的命中角最大.

图1

(1)沿着贴近球场边线AB的直线推进;

(2)沿与底线成45°夹角的直线CD推进,并推广到推进路线与底线成α角的情形.

3.1 问题探源

本题源于历史上经典的米勒问题.1471年,德国数学家、天文学家米勒向教授提出了一个有趣的问题:在地球表面的什么部位,一根垂直的悬杆呈现最长(即可视角最大)?上述最大视角问题因是米勒首先提出的,故被称为“米勒问题”.米勒问题广泛存在于各种实际问题中,例如探求欣赏一幅画的最佳角度、足球比赛最佳射门点等.

3.2 问题转化

将上述模型一般化,可得到如下数学问题:如图2,设M、N是锐角∠AOB的边OA上的两点,试在边OB上找一点P,使得∠MPN最大.

图2

对上述米勒问题,我们有如下重要的米勒定理:

已知点M、N是∠AOB的边OA上的两个定点,点P是边OB上一动点,则当且仅当ΔMPN的外接圆与边OB相切于点P时,∠MPN最大.

结合米勒定理,对于文中的解析几何试题,我们可从另外一个视角给出解答.

评注：最大视角问题在各类试题中频频亮相,常常以解析几何、平面几何和实际应用为背景进行考查,若能从题设中挖掘出隐含其中的米勒问题模型,并能直接运用米勒定理解题,将会突破思维瓶颈、大大减少运算量、降低思维难度,从而使得问题顺利解决.

3.3 真题溯源

以米勒问题为背景的最大张角问题在历年高考试题中屡见不鲜而又经久不衰,如1986年高考全国卷理科第5题、2005年高考浙江卷理科17题、2010年高考江苏卷17题等.若能从题设中挖掘、识别出隐含的米勒问题模型,将有效的突破思维瓶颈、大大减少运算量、降低思维容量,从而使得问题顺利解决.倘若无法及时提取该模型,很容易成为考生难以逾越的鸿沟,下面给出几道真题以示参考.

例1 (2004年全国卷)在直角坐标系中,给定两点M(1,4),N(-1,2),在x轴的正半轴上求一点P,使得∠MPN最大,则点P坐标为.

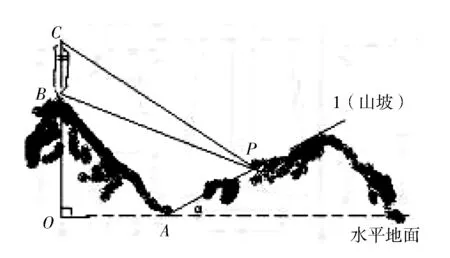
图3

例3 (2005年浙江高考题节选)已知椭圆的中心在原点,焦点F1、F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1;若点P在直线l上运动,求∠F1PF2的最大值.

4 结语

本文通过研究一道解几题解法,获同类问题的一般求解,即巧妙借助米勒定理处理此类问题,达到目标明确,过程简洁,事半功倍之效.数学家波利亚曾说过:“掌握数学就意味着善于解题”.所以数学问题的解决仅仅是一个开端,更重要的是解题后的反思与回顾,以便深刻地揭示问题的本质.在解题教学的过程中,教师要多引导学生多角度思考解题思路,深入挖掘问题本质,寻求巧妙的解题方法,并及时归纳总结规律和结论,从而提高教学效率.