一道模拟试题的命制背景探究

广东省佛山市顺德区容山中学 (528303) 李 云

在高考或模拟试题中,函数与导数板块常常作为压轴题进行考察,此类试题涉及到的变量较多,形式多样,思维性强.但此类试题一般都具有隐藏的几何意义,若通过其几何背景进行理解,即可快速地获得其命制的背景及原理.本文以我市2023届一模第22题为例,探讨其命制背景.

一、试题及分析

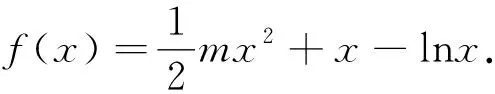
(1)讨论f(x)的单调性;

(2)若a,b是f(x)的两个极值点,且a>b,求证:2[f(a)-f(b)]<(4m+1)(a-b).

分析：本题的第(1)问考察函数单调性,需要通过分类讨论的思想判断,考察导数的基本应用.本题第(2)问涉及到极值点的意义,所证不等式涉及到了三个变量,如何进行转化与消元是解决此题的关键.

二、解法呈现

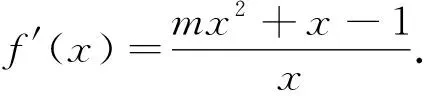
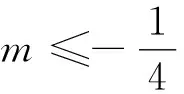
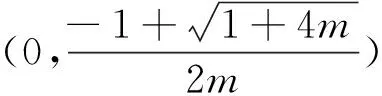
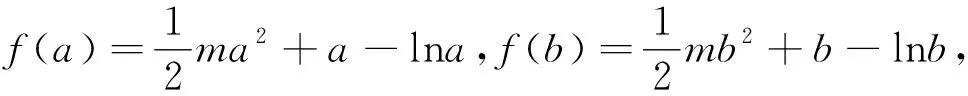
在上述求解过程中,首先利用韦达定理进行了消元,再通过齐次化的技巧将未知量降为1个,充分地体现了转化与划归的思想.后转化后所需证不等式的本质是对数均值不等式.

三、试题背景分析及拓展

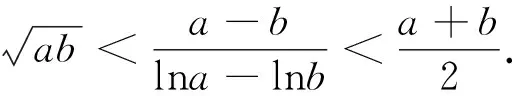
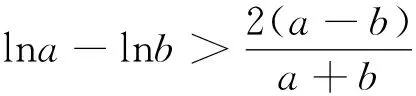
特别地,我们可以取其他的等分点来命制出新的问题,例如:

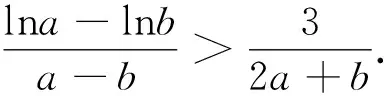
回到原问题,是否也可以通过斜率的比较来解释所证不等式呢?

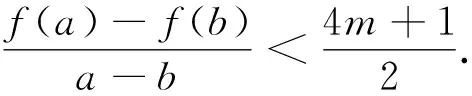
设点M(a,f(a)),N(b,f(b)),则有

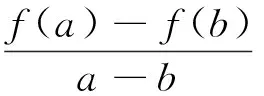
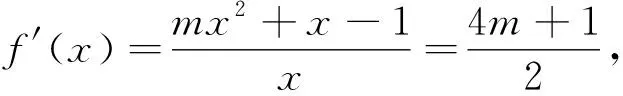
通过上式,我们发现存在两个点满足不等式,现解释如下:

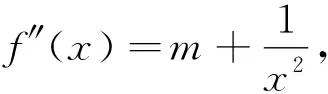
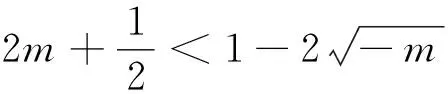
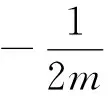
根据上述分析,我们可根据拐点命制如下的练习题供大家参考:

已知函数f(x)=-2x3+9mx2-12m2x+1有两个极值点a,b,且a>b,求证:2[f(a)-f(b)]<3m2(a-b).

注意到该函数的拐点是两个极值点的中心点,我们也可以利用拐点“偏移”的函数来命制其他练习题,请感兴趣的读者自行研究,本文不再赘述.