从一道质检题谈与导数交汇的热点问题

福建省莆田哲理中学 (351100) 郑丽贞

《中国高考评价体系》明确指出“四翼”的高考考查要求,即分别从基础性、综合性、应用性、创新性的角度对素质教育的目标进行评价.其中综合性要求对不同层面的知识、能力、素养能够纵向融会贯通.近年高考对函数和导数的考查侧重于理解和应用,试题有一定的综合性,并与数学思想方法紧密结合.解决该类问题,往往需要充分结合几个知识模块的知识,考生在面临多模块知识交汇时,因综合性较强而产生畏难情绪,导致不能较好作答.本文笔者从一道高三质检题谈起,探究此类问题的破解之道.

引例(2022年鄂东南省级示范校联盟联考)己知函数f(x)=asin(1-x)+lnx,a∈R．

(1)讨论函数f(x)在x∈(0,1)上的单调性;

分析:本题以含三角函数及对数函数的初等函数为载体,与不等式相结合.第一问考查的是导数的应用,利用导数判断函数的单调性基础知识,考查运算求解能力,考查函数与方程思想、分类与整合思想等;第二问考查的是利用导数证明不等式等基础知识,考查抽象概括能力、推理论证能力,考查化归与转化思想、函数与方程思想、分类与整合思想等.考查数学抽象、直观想象、逻辑推理、数学运算等核心素养,体现综合性、应用性、创新性.由于本题涉及三角函数、函数导数、不等式等几个知识板块的交汇,有一定的难度.

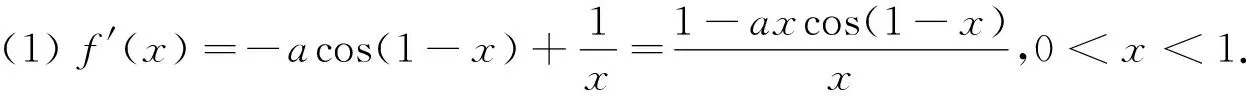
当a≤0时,f′(x)>0,此时f(x)在区间(0,1)单调递增;当00,此时f(x)在区间(0,1)单调递增;

当a>1时,令h(x)=1-axcos(1-x),01,cos(1-x)>0,sin(1-x)>0,所以h′(x)<0,h(x)在区间(0,1)单调递减．又因为h(0)=1>0,所以h(1)=1-a<0,则h(x)在(0,1)上存在唯一零点x0,使得h(x0)=1-ax0cos(1-x0)=0,所以当x∈(0,x0)时h(x)>0,f′(x)>0,f(x)递增;当x∈(x0,1)时h(x)<0,f′(x)<0,f(x)递减．

综上,当a≤1时,f(x)在区间(0,1)单调递增;当a>1时,当x∈(0,x0)时,f(x)在区间(0,1)单调递增;当x∈(x0,1)时,f(x)在区间(0,1)单调递减．其中x0为方程ax0cos(1-x0)=1的根．

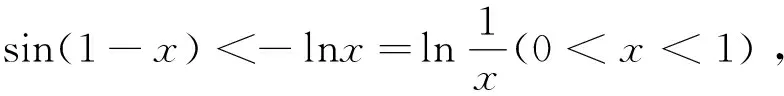
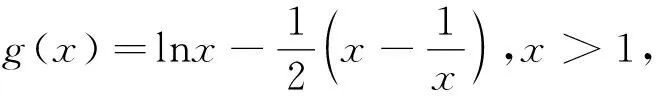
当前高考从能力立意转变为素养导向,素养导向的高考命题注重科学思维的考查,要求学生以严谨的科学思维、严肃的科学态度去思考每一个实际问题.这道试题充分地考查学生三角函数、函数导数、不等式等必备知识以及综合关联各个知识模块思考的关键能力,很好地考查了学生的素养.这种命题方向在近年高考中也频频出现,让人眼前一亮.

一、与三角函数交汇

例1 已知函数f(x)=ex-2x-cosx.

(1)当x∈(-∞,0)时,求证:f(x)>0;

(2)若函数g(x)=f(x)+ln(x+1),求证:函数g(x)存在极小值.

解析:(1)依题意,f′(x)=ex-2+sinx,当x∈(-∞,0)时,f′(x)<0,故函数f(x)在区间(-∞,0)单调递减,故f(x)>f(0)=0.

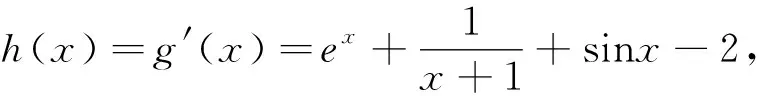
(1)求f(x)在(-π,π)上的单调区间;

(2)设f(x)是f′(x)的导函数,函数g(x)=(2a-1)x+(a+2)xcosx-sin2x+f′(x),若g(x)>0对x∈(0,+∞)恒成立,求a的取值范围．

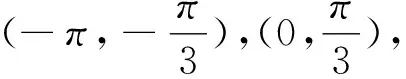
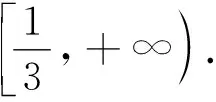
二、与不等式交汇

例2 已知函数f(x)=ln(1+3x)-ax(a≥0).

(1)讨论f(x)的单调性;

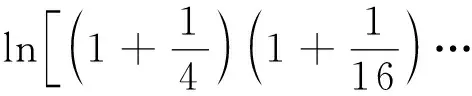
变式2 已知函数f(x)=x2-x-alnx(a>0).

(1)讨论函数f(x)的单调性;

(2)①若f(x)≥0,求实数a的值;

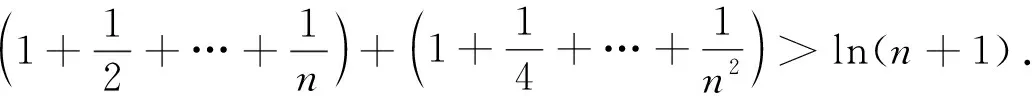
(2)①a=1.②略.

三、与数列交汇

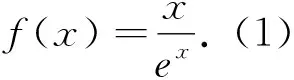
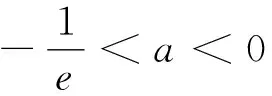
综上,符合题设的实数a的取值范围是(-∞,-1]．

(方法2)同方法1,若a≥0时,g(x)在(0,+∞)上唯一的极大值点,不合题设．

综上,所求实数a的取值范围是(-∞,-1]

图1

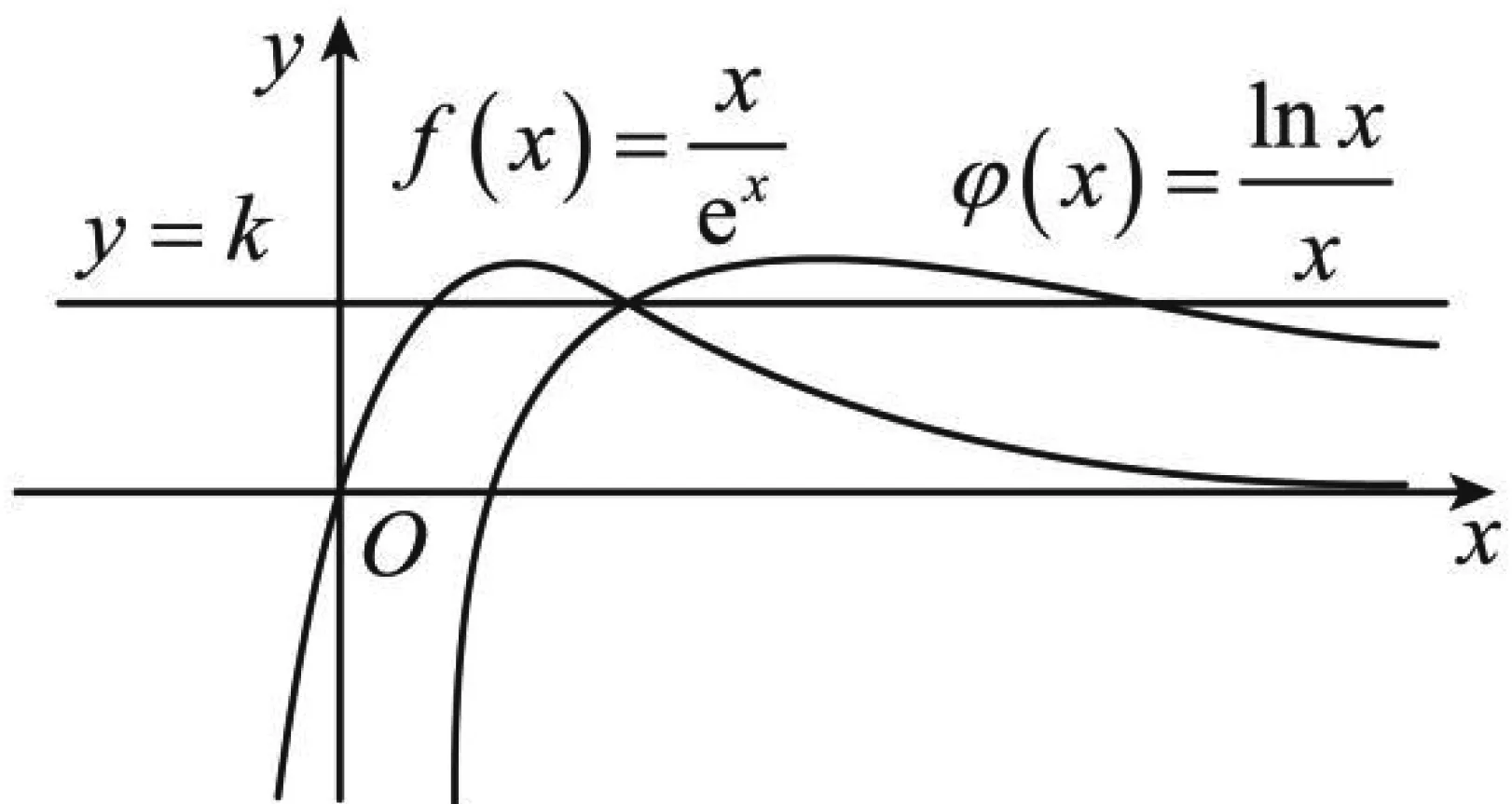
图2

所以x1,x2,x3成等比数列．

评析：本题第(1)问利用导数分类讨论函数单调性,满足函数有唯一的极值点且为极小值点时,确定实数a的取值范围;第(2)问利用导数研究函数单调性,作出函数的大致图象,数形结合找到x1,x2,x3的位置,代入函数解析式化简可得结论.

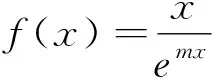
答案：(1)m=1;(2)略.

四、教学启示

高考与各地市质检试题是命题专家智慧的结晶,对高考备考的重要性不言而喻.一线教师需认真口味,从不同角度对试题进行剖析,引导学生在解决问题的过程中,能在思想方法层面上去提炼反思,加深对数学问题本质理解,进而构建知识体系.当前高考考查素养强调创新,教师要善于对一些综合问题进行情景变式探究,引导学生积累解题活动经验,在变化的情境中寻找不变的本质,拓展数学思维,提升数学能力,发展数学核心素养.