具有时变时滞的分数阶四元数神经网络的投影同步
李春美, 杨绪君, 吴 香
(重庆交通大学 数学与统计学院,重庆 400074)
0 引 言
近年来,神经网络在模式识别[1]、联想记忆、信号处理[2]和安全通信等领域的广泛应用,引起了许多研究者的关注[3].由于分数阶模型相比传统的整数阶模型,有很好的遗传性和记忆性,能更准确地描述复杂系统的动力学行为,因此,许多学者开始研究分数阶神经网络,并得到了显著的研究成果[4-6].
同步现象作为神经网络的一种重要的动态行为,是分数阶神经网络研究的一个热点问题,包括完全同步[7]、准同步[8]和Mittag-Leffer同步[9].文献[10]研究了一类分数阶复值神经网络的准投影同步和完全同步问题,通过设计合适的线性反馈控制器和自适应控制,利用Laplace变换和Mittag-Leffler函数的性质建立了一个新的分数阶微分不等式.目前,已有许多学者对神经网络的投影问题进行了深入研究[11-13].文献[14]利用复变函数和Mittag-Leffler函数的理论讨论了分数阶递归复值神经网络的拟投影同步.文献[15]研究了分数阶复值记忆神经网络的投影同步问题,根据分数阶多时滞系统的稳定性定理和比较原理,得到了保证驱动响应网络同步的一些判据.文献[16]研究了一类分数阶延迟神经网络的驱动响应同步问题.
以上关于神经网络的研究,都是关于实值或复值神经网络的,但在实际应用中,会遇到多维数据,实值神经网络和复值神经元无法很好地处理这些数据.而四元数由一个实部和三个虚部组成,可以有效地处理多维数据.因此,一些学者将四元数引入到经典的神经网络中,建立了四元数神经网络[17-18].与实值神经网络和复值神经网络相比,四元数神经网络的存储容量大,可处理多维信息,应用于图像处理、计算机图形学、彩色夜视等领域[19-20].文献[21]将分数阶四元数神经网络分解成四个实值部分,通过分数阶微分不等式,设计合适的控制器,研究了分数阶四元数神经网络的投影问题.文献[22-24]将四元数神经网络分解为两个复值系统或四个实值系统.虽然这种分离方法是可行和有效的,但它导致了模型维数增加,增强了理论分析的复杂性.文献[25]研究了具有时滞和参数不确定的四元数神经网络的鲁棒性问题.目前,将四元数神经网络同步性问题当作一个整体来研究尚不多见.
鉴于此,本文研究了具有时变时滞的四元数神经网络的投影同步问题.通过选取合适的Lyapunov-Krasovskii泛函,结合积分不等式,得到了网络投影同步的不等式判据.
注1H表示四元数斜域,Hn和Hn×n分别表示n维四元数空间和n×n四元数矩阵集.AT和A*分别表示矩阵A的转置矩阵和共轭转置矩阵.
1 预 备 知 识
四元数可以写成q=q0+q1i+q2j+q3k,其中q0,q1,q2,q3∈R,i,j,k为虚数单位,满足下列条件:
i2=j2=k2=-1,ij=-ji=k,jk=-kj=i,ki=-ik=j.
由此,可以看出四元数乘积不满足交换律.如果p=p0+p1i+p2j+p3k∈H,q=q0+q1i+q2j+q3k∈H,则p与q的和定义为
p+q=(p0+q0)+(p1+q1)i+(p2+q2)j+(p3+q3)k;
p与q的积定义为
pq=(p0q0-p1q1-p2q2-p3q3)+(p0q1+p1q0-p2q3-p3q2)i+
(p0q2+p2q0-p1q3+p3q1)j+(p0q3+p3q0+p1q2-p2q1)k.
四元数q的共轭定义为
四元数q的模定义为
定义1(分数阶积分) 设f(t)∈Hn在[t0,+∞)是分段连续的函数,函数f(t)的分数阶积分定义为
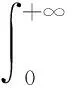
定义2(Riemann-Liouville分数阶导数) 设f(t)∈Hn在[t0,+∞)是可微的函数,函数f(t)的分数阶导数定义为
其中
m-1<α 引理1[5]若z(t)∈R是连续可导的函数,且z(t)的导数是可积的,则对∀t>0,α∈(0,1),下面的不等式成立: 引理2 若p(t)∈H是连续可微的函数,M为正定的Hermite矩阵,则对∀t>0,α∈(0,1),下面的不等式成立: 证明由于M为正定的Hermite矩阵,则存在一个酉矩阵W∈Hn×n与正定的对角阵Λ=diag(λ1,λ2,…,λn),使得M=WΛW,其中λm(m=1,2,…,n)是矩阵M的特征值. 令 U(t)=Wp(t)=(U1(t),U2(t),…,Un(t))T,Um(t)=xm(t)+iym(t)+jzm(t)+kum(t), 则 由引理2得 引理3[17]Q∈Hn×n为正定的Hermite矩阵,向量函数u(x):[a,b]→Hn,a 引理4[24]Q∈Cn×n为正定的Hermite矩阵,向量函数u(x):[a,b]→Cn,a 引理5Q∈Hn×n为正定的Hermite矩阵,向量函数u(x):[a,b]→Hn,a 本文考虑如下一类具有时变时滞分数阶四元数神经网络: (1) 其中0<α<1,p(t)=(p1(t),p2(t),…,pn(t))T∈Hn表示系统的状态向量;E=diag(e1,e2,…,en)表示自反馈矩阵,ei>0,i∈1,2,…,n;σ(t)表示时变时滞;A,B分别表示t和t-σ(t)时刻的连接权矩阵;向量激活函数f(p(t))=(f1(p1(t)),f2(p2(t)),…,fn(pn(t)))T∈Hn,g(p(t-σ(t))=(g1(p1(t-σ(t))),g2(p2(t-σ(t))),…,gn(pn(t-σ(t))))T∈Hn;L表示相应的外部输入. 本文做假设如下. 假设1 对任意的x,y∈H,存在两个正常数λi,γi(i=1,2,…,n),使得 |fi(x)-fi(y)|≤λi|x-y|,|gi(x)-gi(y)|≤γi|x-y|. (2) 令 Λ=diag(λ1,λ2,…,λn),Γ=diag(γ1,γ2,…,γn). 假设2 时滞σ(t)是连续可导的,且满足如下条件: (3) 考虑响应系统如下: (4) 其中u(t)为控制器.控制器设计如下: u(t)=-K(q(t)-Fp(t))+EFp(t)-FEp(t)-Af(Fp(t))+FAf(p(t))- Bg(Fp(t-σ(t)))+FBg(p(t-σ(t)))-(I-F)L, (5) 其中K∈Rn×n是控制器u(t)的系数矩阵,I为单位矩阵. 定义误差为 θ(t)=q(t)-Fp(t), (6) 其中 θ(t)=(θ1(t),θ2(t),…,θn(t))*∈Hn,F=diag(F1,F2,…,Fn)>0. 则由系统(1)和系统(4)得到误差系统如下: (7) 其中 g(θ(t-σ(t)))+Fp(t-σ(t)))-g(Fp(t-σ(t))). (8) 证明选择如下Lyapunov泛函: V(t)=V1(t)+V2(t)+V3(t), (9) 其中 (10) (11) (12) 对V1(t),V2(t),V3(t)求导,得 θ*(t)(-P1(E+K)-(E+K)*P1+(E+K)*P2(E+K))θ(t)+ (13) (14) (15) 在假设1条件下,存在正定对角矩阵K1,W,有 (16) (17) 由式(13)—(17)可知 (18) 其中 根据Lyapunov理论,可知系统(1)和系统(4)是投影同步的. 注2 当系统(1)的时变时滞退化成常时滞时,相应的驱动系统和响应系统为 (19) (20) 其中控制器u(t)=-K(q(t)-Fp(t))+EFp(t)-FEp(t)-Af(Fp(t))+FAf(p(t))-Bg(Fp(t-σ))+FBg(p(t-σ))-(I-F)L. 推论1 若假设1成立,如果存在正定的Hermite矩阵Pi(i=1,2,…,6),两个正定的对角矩阵K1,W,满足如下线性矩阵不等式: (21) 其中Π11=-(E+K)*P1-P1(E+K)+(E+K)*(P2+σ2P4+σ4P6)(E+K)+ΛK1Λ+ΓWΓ,Π12=P1A-(E+K)*(P2+σ2P4+σ4P6)A,Π13=P1B-(E+K)*(P2+σ2P4+σ4P6)B,Π14=-(E+K)*P3,Π15=-σ3(E+K)*P5,Π22=A*(P2+σ2P4+σ4P6)A-K1,Π23=A*(P2+σ2P4+σ4P6)B,Π33=B*(P2+σ2P4+σ4P6)B-W. 根据Lyapunov理论,可知系统(1)和系统(4)是投影同步的. 注3 文献[26]研究了分数阶四元数值神经网络的同步性,但没有考虑时滞.该模型是本文研究模型的特例,本文研究的模型更符合实际,研究结果也更具有普遍性. 例1 考虑以下二维的时变时滞分数阶四元数神经网络作为驱动系统: (22) 其中α=0.98,σ(t)=|sin(2t)|,p(t)=(p1(t),p2(t))T∈H2,f1(p(t))=f2(p(t))=g1(p(t))=g2(p(t))=0.25tanh(p(t)), 对应的响应系统为 (23) (24) 当Λ=diag(0.25,0.25)时,Γ=diag(0.25,0.25),满足假设1和假设2. 利用MATLAB对线性矩阵不等式(8)求得可行解为 因此,定理1的条件成立,从而系统(7)的零点是稳定的,即系统(4)和系统(1)可以实现投影同步.数值仿真选取如下初始条件: p0=[4.5+0.9i-3.5j-2k,4.5-0.9i-5.5j+2k]T, q0=[-5.5-2i-3.5j-5k,-1.5-3i-7.5j+5k]T. 图1、图2给出了驱动系统(1)和响应系统(4)在未施加控制时状态变量的时间响应曲线,图3给出了误差系统(7)在未施加控制时状态变量的时间响应曲线. 图1 未加控制时,状态变量的时间响应曲线Fig.1 The time response curves of state variables without control 图2 未加控制时,状态变量的时间响应曲线Fig.2 The time response curves of state variables without control 图3 未加控制时,误差变量的时间响应曲线Fig.3 Time response curves of error variables without control注 为了解释图中的颜色,读者可以参考本文的电子网页版本,后同. 当投影系数矩阵F取为F=diag(1,1),驱动系统(1)和响应系统(4)完全同步.图4、图5给出了驱动系统(1)和响应系统(4) 在施加控制时状态变量的时间响应曲线.图6给出了误差系统(7) 在施加控制时状态变量的时间响应曲线. 图4 投影矩阵为F=diag(1,1),施加控制时,状态变量的时间响应曲线Fig.4 Projection matrix F=diag(1,1),and the time response curves of state variables with control 图5 投影矩阵为F=diag(1,1),施加控制时,状态变量的时间响应曲线Fig.5 Projection matrix F=diag(1,1),and the time response curves of state variables with control 图6 投影矩阵为F=diag(1,1),施加控制时,误差变量的时间响应曲线Fig.6 Projection matrix F=diag(1,1),and the time response curves of error variables 当投影系数矩阵F取为F=diag(-1,-1),驱动系统(1)和响应系统(4)反同步.图7、图8给出了驱动系统(1)和响应系统(4)在施加控制时状态变量的时间响应曲线.图9给出了误差系统(7)在施加控制时状态变量的时间响应曲线. 图7 投影矩阵为F=diag(-1,-1),施加控制时,状态变量的时间响应曲线Fig.7 Projection matrix F=diag(-1,-1),and the time response curves of state variables with control 图8 投影矩阵为F=diag(-1,-1),施加控制时,状态变量的时间响应曲线Fig.8 Projection matrix F=diag(-1,-1),and the time response curves of state variables with control 图9 投影矩阵为F=diag(-1,-1),施加控制时,误差变量的时间响应曲线Fig.9 Projection matrix F=diag(-1,-1),and the time response curves of error variables 如图1、2、3所示,状态变量的时间响应曲线验证了在不施加控制时,驱动系统(1)和响应系统(4)不同步,误差系统(7)是不稳定的.在施加控制时,图6和图9表明误差系统(7)是稳定的.当投影系数矩阵F取为F=diag(1,1),图4和图5表明驱动系统(1)和响应系统(4)完全同步;当投影系数矩阵F取为F=diag(-1,-1),图7和图8表明驱动系统(1)和响应系统(4)反同步. 本文研究了具有时变时滞的四元数神经网络系统投影同步问题.在合适的控制器下,通过构造合适的Lyapunov函数,并利用一些不等式技巧,得到了具有时变时滞分数阶四元数时滞神经网络的投影同步的充分性判据.最后通过数值仿真实例验证了所得结论的有效性和可行性.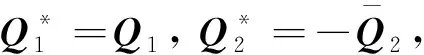
2 模 型 描 述
3 主 要 结 论
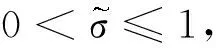
4 数 值 例 子










5 结 论

