考虑页岩塑性变形的水力裂缝与天然裂缝相交模拟研究

曹玉玲, 何强胜, 刘 闯

(南京工业大学 土木工程学院,南京 211816)

0 引 言

水力压裂已经成为油气生产过程中和商业开发中不可缺少的技术[1-4],在非常规油气藏的勘探中得到了广泛的应用．实际上,地层是异质性的,即包含许多地质不连续性,如断层[5]、层理面[6-7]和天然裂缝[8-10]等,因此水力压裂裂缝的演化将会变得更加复杂．储层的异质性在颗粒尺度[11]和宏观尺度[12]上均已被证实．储层异质性将会引起地层内初始地应力的非均匀分布,进而影响压裂中水力裂缝的演化[13]．水力裂缝与天然裂缝或层理面相遇之后,可以观察到三种相互作用模式,即贯穿、融合和分支[14-15]．数值计算中对储层异质性的忽略已被证实会导致与实际水力裂缝扩展形成巨大偏差[16]．另外,在压裂过程中,水力裂缝的扩展特性和几何形态还会受到地层岩石塑性变形的影响[17],特别是在塑性较强的油气储层中,这种影响会变得更加明显,因此,忽略岩石塑性变形可能会造成裂缝扩展形态与流体压力的预测结果出现较大的偏差[18]．基于线弹性断裂力学[19-20]提出的裂缝扩展理论与方法不再适用于塑性地层[21]．

目前,许多学者在水力裂缝和天然弱界面的相互作用方面做了大量的研究[22-25]．研究发现,水力裂缝与不同胶结强度的天然裂缝相互作用会促进裂缝形态的复杂性[26]．Wan等[27]通过真三轴压裂模拟实验研究了天然裂缝尺寸对水力裂缝扩展的影响,得出泵压曲线与裂缝几何形状之间的关系．Zhou等[28]通过巴西圆盘试验,研究了不同天然裂缝填料对裂缝扩展的影响．实验表明,天然裂缝的存在对水力裂缝的扩展过程起着极其重要的作用．基于岩石力学的理论与方法,陈治喜等[29]构建层状地层数值模型,研究了水力裂缝在垂直方向上的扩展特性,并讨论了压裂液黏度、 地应力差与地层断裂韧性等参数对垂直方向上裂缝形态的影响．水力裂缝的扩展取决于不同胶结强度的天然弱界面的剪切滑移,这个结论在数值模拟和真三轴水力压裂实验中均被证实[30-31]．研究表明,在异质性储层中,水力裂缝与天然裂缝相交后,天然裂缝的破坏模式可能会从张拉破坏转变为混合模式或剪切破坏[32]．以上实验研究与数值模拟只考虑了线弹性地层的水力裂缝扩展,没有考虑岩石的塑性变形对水力裂缝的影响．另外,部分学者在岩石塑性变形对水力裂缝演化特性的影响方面也开展了一些研究[33-35]．Zeng等[36]构建了具有塑性的多孔岩石数值模型,采用Drucker-Prager准则描述了地层岩石的塑性应变．基于线性断裂力学理论,Zhao等[37]得出了水力压裂裂缝扩展时应力强度因子的变化规律,通过应力强度因子预测水力裂缝是否能够贯穿层理面,但并未考虑天然裂缝对水力裂缝扩展形态的影响．结合有限元和有限差分法,Papanastasiou[38-39]构建了二维数值模型,压裂过程中涉及地层的塑性变形、水力裂缝的扩展与裂缝内流体流动的非线性耦合,数值结果表明地层塑性变形显著影响裂缝的演化．

从以上提到的研究结果发现,岩石的塑性变形、 天然裂缝与层理面都会对水力裂缝的扩展形态造成影响．然而,在弹塑性地层中,同时考虑天然裂缝和层理面对水力裂缝影响方面的研究还不够深入．因此,本文对存在层理面和天然裂缝的弹塑性地层中,水力裂缝的扩展形态进行了数值模拟研究,并分别讨论岩石的塑性变形、地应力差和注入速率等参数对水力裂缝扩展形态的影响．

1 弹塑性地层数学模型

本文假设地层是各向同性且均匀的多孔介质,并考虑了岩石的塑性变形．该数学模型包含以下三个部分:① 地层岩石变形、② cohesive单元模型、③ 方程的离散化．

1.1 地层岩石变形

一个外部边界为∂Ω的有界域Ω⊂d(d=2,3;d表示空间维数),域Ω上的外部边界∂Ω由∂Ωt和∂Ωu两个不连续部分组成．Γ⊂d-1是内部不连续边界,它可以作为∂Ωt的一部分．流体的注入时间T满足T>0．在域Ω上,位于x位置上的点在时间t∈[0,T]上的位移表示为u(x,t)⊂d．应变张量表示位移矢量相对于域内位置的对称梯度,ε(x,t)=∇su(x,t)=(∇u(x,t)+(∇u(x,t))T)/2．体力b*(x,t)作用在域Ω上,牵引力t*(x,t)作用于边界上．

根据Griffith理论,弹性体积能和裂纹表面能之间的竞争使得裂纹开启并扩展．当裂纹表面所需要的能量达到临界能量释放率Gc时,裂纹出现．裂纹的总能量E(u,Γ)由固体中储存的能量Ψs(u,Γ)、断裂所需的能量Ψc(Γ)、塑性能Ψp(u)与外部势能P(u)组成:

E(u,Γ)=Ψs(u,Γ)+Ψp(u)+Ψc(Γ)-P(u)．

(1)

结合积分的形式,固体的能量Ψs(u,Γ)、断裂能Ψc(Γ)、塑性能Ψp(u)以及外部势能P(u)可分别表示为

(2)

式中,Ψp(u)是塑性能,取决于弹性内部变量参数κ;ψe(εe,Γ)是弹性能量密度函数,它可以用裂纹长度Γ和弹性应变张量εe(u)表示;临界能量释放率Gc是材料的属性参数．裂纹表面的流体压力满足t*=pfn,其中n表示裂纹表面的单位法向量．

(3)

或者

(4)

可以得到

δE=(-G+Gc)δΓ≥0 ⟹G-Gc≤0,

(5)

式中,G= -∂Ψs/∂Γ为能量释放率;σ=∂ψe/∂εe为Cauchy应力张量．ε=εe+εp为总应变张量,其中,εe是弹性应变张量;εp是塑性应变张量．弹性能密度ψe(εe)可以表示为

(6)

式中,λ和ν是Lamé常数．根据Karush-Kuhn-Tucker条件与相关的流动准则,塑性应变的演化与塑性内部的变量可以表示为

(7)

(8)

(9)

硬化函数表示为

(10)

式中,材料参数α,β,c,ξ和hr0可以通过单轴压缩实验得到．

1.2 Cohesive单元模型

关于黏度为μ的不可压缩Newton流体,裂缝内的流体流动近似于两个平行板之间的流动．压力梯度与裂缝宽度共同决定裂缝内的局部流体流速[41]:

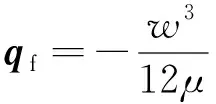
(11)

式中,w是裂缝的宽度;pf表示裂缝内部的流体压力．根据润滑方程,裂缝内的流体质量守恒方程表示为

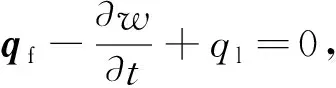
(12)

式中,ql表示地层中由于单位裂缝表面积上的滤失引起的局部流体损失．裂缝到周围岩石的滤失行为表示为

ql=cl(pf-pm),

(13)

式中,pm是裂缝附近的孔隙压力;cl是一个常数,表示压力相关的滤失系数．

根据Darcy定律,岩石基质内的流体扩散表示为

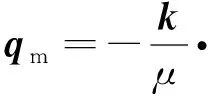
(14)

式中,k表示岩石渗透率张量;qm表示多孔介质内的流体流速矢量;饱和的多孔介质内,总应力σi,j与有效应力σ′i,j的关系式为[42]

σi,j=σ′i,j+αpw,

(15)

式中,pw表示孔隙压力,α是多孔弹性常数．在t时刻岩石的变形下,根据体积的虚功原理形式,多孔介质的弹性平衡方程表示为

(16)

式中,I是单位矩阵;t表示单位面积上的张拉力;f表示单位体积力;δ表示虚分量;δε与δv分别表示虚变形率和虚位移．流体质量连续性方程在体积V内的流体总质量的变化率与穿过表面S上的流体的质量速度条件可以表示为

(17)

式中,n指表面S上的外向法线;vw表示流体速度;ρw是流体的质量密度;nw表示孔隙率;本文中裂缝的开启与扩展基于黏聚区单元,其中,通过黏性势函数,牵引力T与一对黏性表面的位移δ的关系表示为

(18)

本文使用双线性牵引分离定律[43]来表示牵引力与分离位移之间的关系．其中,对于弹性介质,岩石的断裂能与断裂韧性KIC的关系通过Poisson比ν与弹性模量E来表示:

(19)

假设裂缝承受的压力达到法向和切向应力时,裂缝的损伤开始．因此,二次应力起裂准则表示为

(20)

(21)

(22)

式中,Tmax表示抗拉或抗剪强度;裂缝完全破坏之前,应力与位移之间的关系为

(23)

式中,dz表示黏聚区表面的初始厚度,其方程表示为

(24)

裂缝完全破坏之后材料的软化方程为

(25)

对于损伤因子D,其表示为[44]

(26)

对于有效位移δm,其表示为[45]

(27)

式中,δn,δs和δt分别表示法向、第一与第二剪切位移分量．

根据Coulomb摩擦定律,裂缝表面发生破坏但仍相互接触时,其剪切滑移表示为[45]

(28)

式中,η0表示摩擦因数;σn和τs分别表示法向压缩应力和摩擦剪应力;τmax表示接触面上切应力的最大限值．

1.3 方程的离散化

本文采用加权残差法进行控制方程的离散化．在忽略体力的前提下,分别在式(4)和式(11)中引入测试函数δu和δpf,并结合相应的边界条件,裂缝内的流体流动方程和固体平衡方程的弱形式可以表示为

(29)

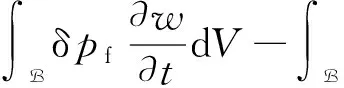
(30)

式中,δε=(∇δu+(∇δu)T)/2表示虚应变;δu表示虚位移;B ⊂d表示断裂面内的区域,Ω表示整个位移场区域．流体压力pf(x,t)、断裂孔径w(x,t)和位移场u(x,t)分别根据流体压力p={pI}T和节点位移d={dI}T进行插值:

(31)

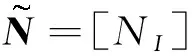
近似得到的压力梯度∇p和离散化应变ε为

(32)

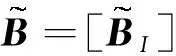
(33)

将式(31)和式(32)代入到式(29)和式(30)的弱形式方程中,非线性方程系统可以表示为

(34)

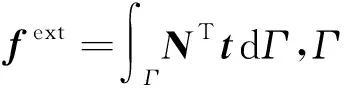
(35)

或者

(36)

式中,K表示刚度矩阵,它的分量表示为

(37)

值得注意的是,方程中的刚度矩阵不是对称的,并且耦合方程要使用非系统求解器进行求解．在本文中,非线性方程组是采用基于单片算法的Newton法进行求解．

2 数值模型的验证

从两个方面验证数值模型的准确性．一方面,通过构建单条裂缝模型与经典KGD模型的解析解[45-47]关于裂缝的半长进行对比验证,数值模型的力学参数如下:弹性模量为15 GPa,Poisson比为0.25,压裂液注入速率为0.001 m2/s,流体黏度为0.1 Pa·s,岩石抗拉强度为1 MPa．图1给出了对比结果,可以看出,数值模拟结果与KGD模型的解析解[45-47]匹配良好．

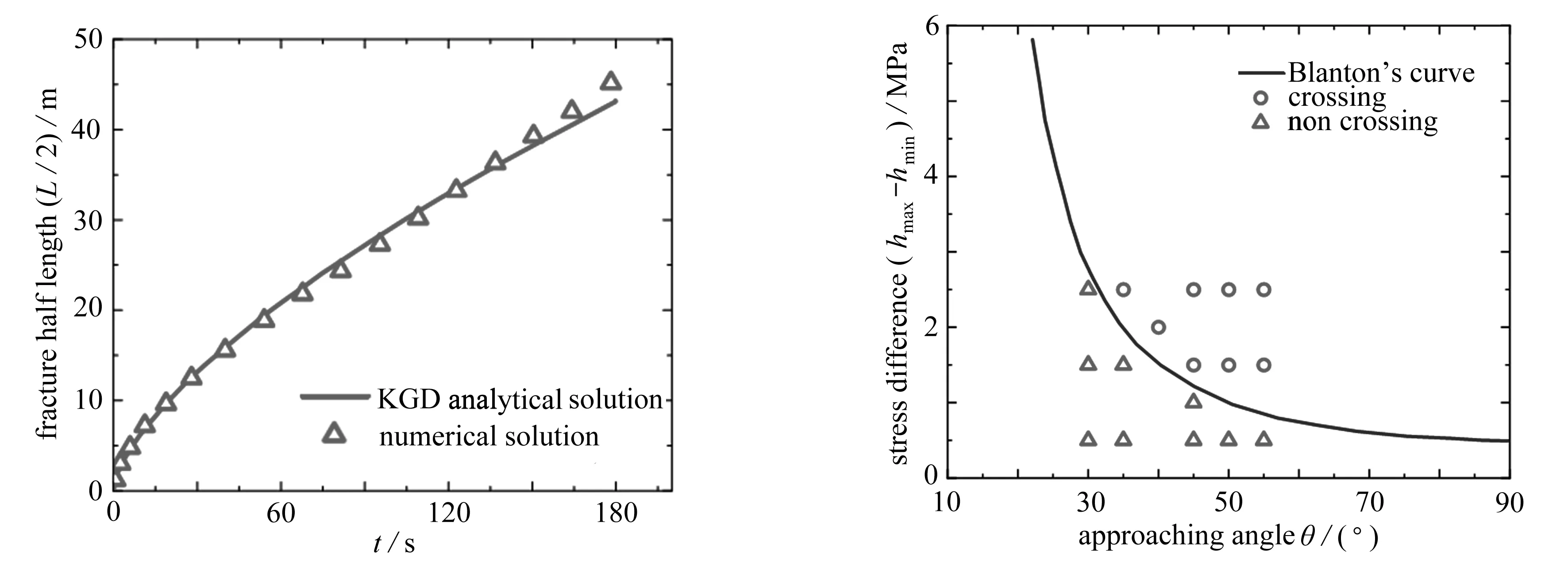
图1 水力裂缝半长-时间的曲线图 图2 水力裂缝与天然裂缝交叉角度-地应力差曲线图Fig.1 The hydraulic fracture half length-time curve Fig.2 The approaching angle between the hydraulic fracture and the natural fracture-stress difference curve

另一方面,通过建立水力裂缝与天然裂缝相互作用的压裂模型与Blanton曲线[48]关于水力裂缝是否贯穿天然裂缝进行对比验证．Blanton曲线[48]是由Science Applications Inc.的Blanton L于真三轴加载水力压裂实验,研究不同水平应力差和交叉角裂缝相交所总结的结果．该曲线将裂缝交叉扩展模式分成两类,即交叉和融合,可方便用于裂缝交叉形态预测,鉴于有大量实验数据作支撑,因而被广泛应用于裂缝交叉数值模型的验证[49-50]．本文数值模型的力学参数如下:岩石的弹性模量为15 GPa,Poisson比为0.25,压裂液的注入速率为0.003 m2/s,流体黏度为0.03 Pa·s,另外,水力裂缝和天然裂缝的抗拉强度分别为2.5 MPa和1 MPa,岩石的渗透率为1 mD(1 mD=9.87×10-4μm2)．对比验证的结果如图2所示,可以看出,数值模拟的结果与Blanton曲线[48]有很好的一致性．

3 数值模拟的结果和讨论

3.1 数值模型

基于有限元法,一个具有分层的弹塑性地层二维平面应变数值模型被构建,如图3所示,半模型的尺寸为20 m×60 m,水平和垂直方向分别对应地层的最小水平主应力方向和垂直主应力方向．地层的材料参数和塑性参数分别如表1和表2所示．表1和表2中的部分参数来源于文献[10,34,51-52]．模型的上边界被设置为对称边界．地层内的储层和隔层均预设了天然裂缝、层理面和水力裂缝的黏聚区单元．天然裂缝和层理面等间距且平行分布在地层内,水力裂缝与层理面的夹角被定义为交叉角．地应力差是储层和隔层的最小水平主应力的差值．水力裂缝的初始射孔方向平行于垂直主应力方向．裂缝中的流体为不可压缩的Newton流体,裂缝内的流体能够向周围的岩石发生滤失．

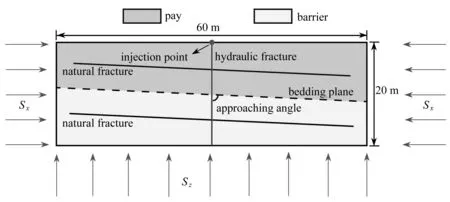
图3 分层页岩模型的几何形状和边界条件Fig.3 Geometric and boundary conditions of the layered shale model

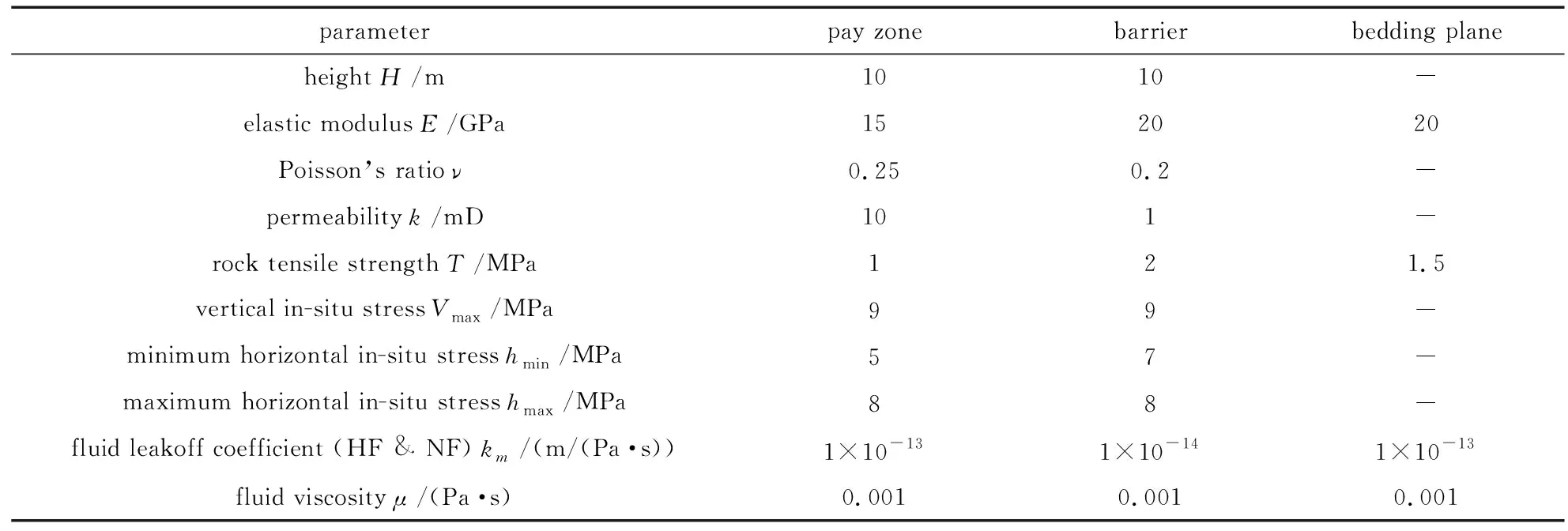
表1 分层页岩的输入参数Table 1 The input parameters of the layered shale

表2 页岩的塑性参数Table 2 The input plastic parameters of the shale

3.2 弹塑性模型与弹性模型的比较以及塑性区的演化

为研究岩石塑性变形对水力裂缝几何形态的影响,分别选取注入速率为0.001m2/s,0.005 m2/s和0.01 m2/s的弹性模型和弹塑性模型进行数值计算．图4显示了在不同注入速率下,弹性和弹塑性模型中裂缝几何形态的变化．

图4 不同注入速率下弹性模型(左)和弹塑性模型(右)裂缝几何形态对比Fig.4 Comparison of crack morphologies between the elastic model (left) and the elasto-plastic model (right)at different injection rates注 为了解释图中的颜色,读者可以参考本文的电子网页版本,后同．

从图4可以看出,在相同的注入速率下,弹塑性模型中的水力裂缝沿着天然弱界面发生扩展,而弹性模中的水力裂缝遇到天然弱界面后仍沿着初始方向扩展．这是因为,裂缝在弹性模型内扩展时,能量主要用于黏性流体的流动和新裂缝的产生;而在弹塑性模型裂缝扩展过程中,其附近形成了一定范围的塑性变形[34],耗散了部分裂缝扩展驱动能量,根据经典弹塑性断裂理论,这可以等效成岩石基质断裂韧性的增加．由于天然裂缝的扩展受Ⅰ型和Ⅱ型断裂共同控制,岩石的塑性变形对其影响更为复杂．此外,塑性变形引起裂缝附近地应力场的重分布也会改变水力裂缝贯穿天然裂缝的难度[50,53-54],模拟发现,岩石的塑性变形有助于促进天然裂缝的开启．

分布在裂缝附近的等效塑性应变(EPS)如图5所示．由图可见,压裂过程中裂缝尖端附近发生明显的塑性屈服,待裂缝进一步地向前扩展之后,已开启的裂缝发生卸载,致使塑性区的范围不再增大．从整体上看,塑性变形区域主要集中在储层内并且是在遇到天然裂缝之前的区域,这主要是由于隔层内岩石弹性模量更高,并且压裂过程中水力裂缝贯穿天然裂缝之后裂缝内的压力急速下降,使得裂缝内的压力达不到塑性屈服应力．岩石塑形变形所引起的能量耗散会抑制水力裂缝的扩展和裂缝交叉行为,形成更短更宽的裂缝．岩石的塑形变形与屈服应力、硬化常量等参数有关,文献[52]详细探讨了这些参数对塑形变形的影响．考虑到裂缝交叉的复杂性,塑形参数对交叉行为的影响仍需要进一步的工作．

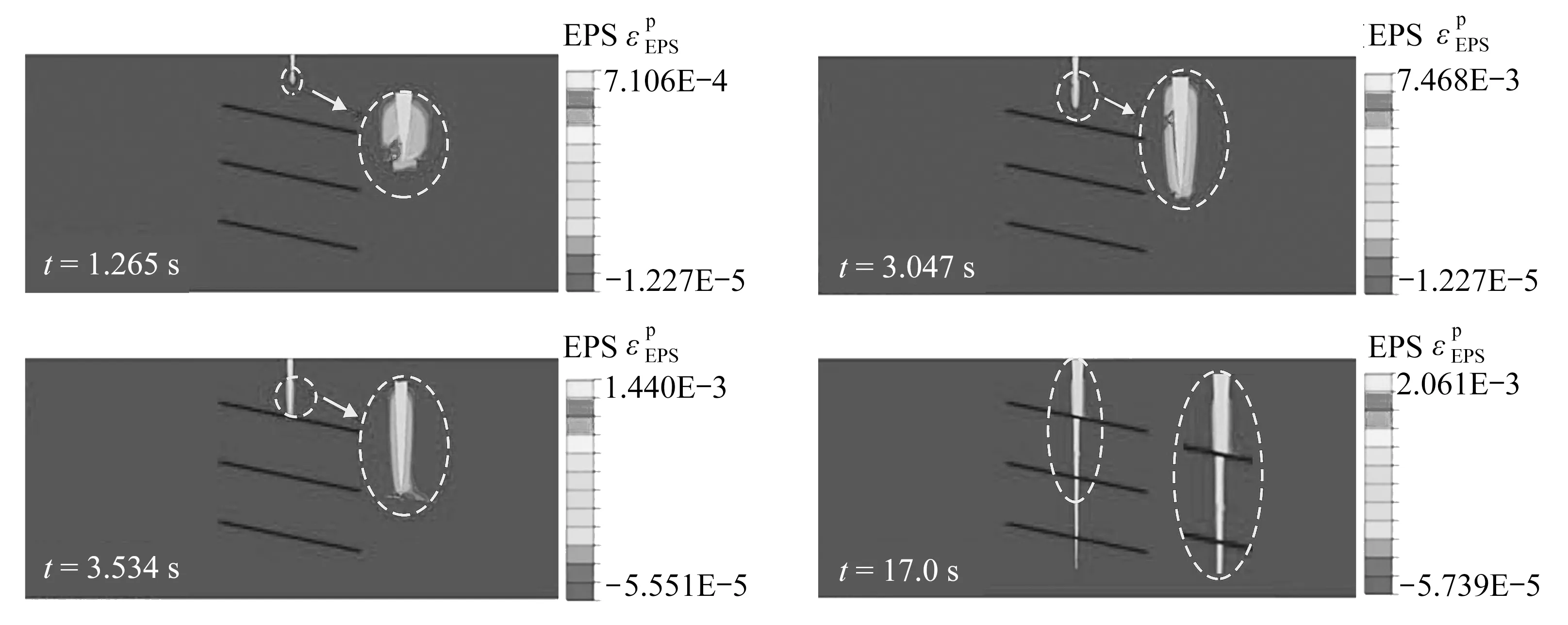
图5 分布在裂缝附近的等效塑性应变Fig.5 Equivalent plastic strains distributed in the vicinity of the crack

3.3 不同断裂模式下的裂缝扩展

本小节研究了储层和隔层中不同水力裂缝强度下裂缝的断裂机制．图6和图7分别采用了两种数值模拟方案,即分别讨论储层和隔层中不同的破裂机制．采用牵引分离定律描述黏聚区单元的起始损伤和损伤演化,如图6(d)所示,三角形的顶点对应裂缝损伤的起始点,左侧边的斜率对应岩石材料的刚度．控制裂缝的断裂能不变,对应的岩石破裂机制分别为脆性破坏、韧性破坏和混合模式．从方案A可以看出,岩石表现为脆性破坏时,水力裂缝沿着层理面偏转,这主要是由于层理面的强度较低．岩石发生混合模式或者韧性破坏时,水力裂缝贯穿层理面,最终沿着隔层的天然裂缝扩展．对于方案B,岩石发生脆性和混合模式破坏时,裂缝的扩展形态与方案A相同,而裂缝发生韧性破坏时,由于隔层内的岩石在较小的牵引力下就能够开启,因此,水力裂缝更容易沿着初始方向扩展．由以上结果分析可以得出,储层和隔层的水力裂缝都在发生脆性破坏时,水力裂缝容易沿着层理面扩展,发生韧性破坏时,水力裂缝倾向于贯穿层理面．

图6 储层和隔层中水力裂缝在不同强度下的断裂机制(方案A)Fig.6 Fracture mechanisms of hydraulic fractures in the pay zone and the barrier at different strengths(plan A)

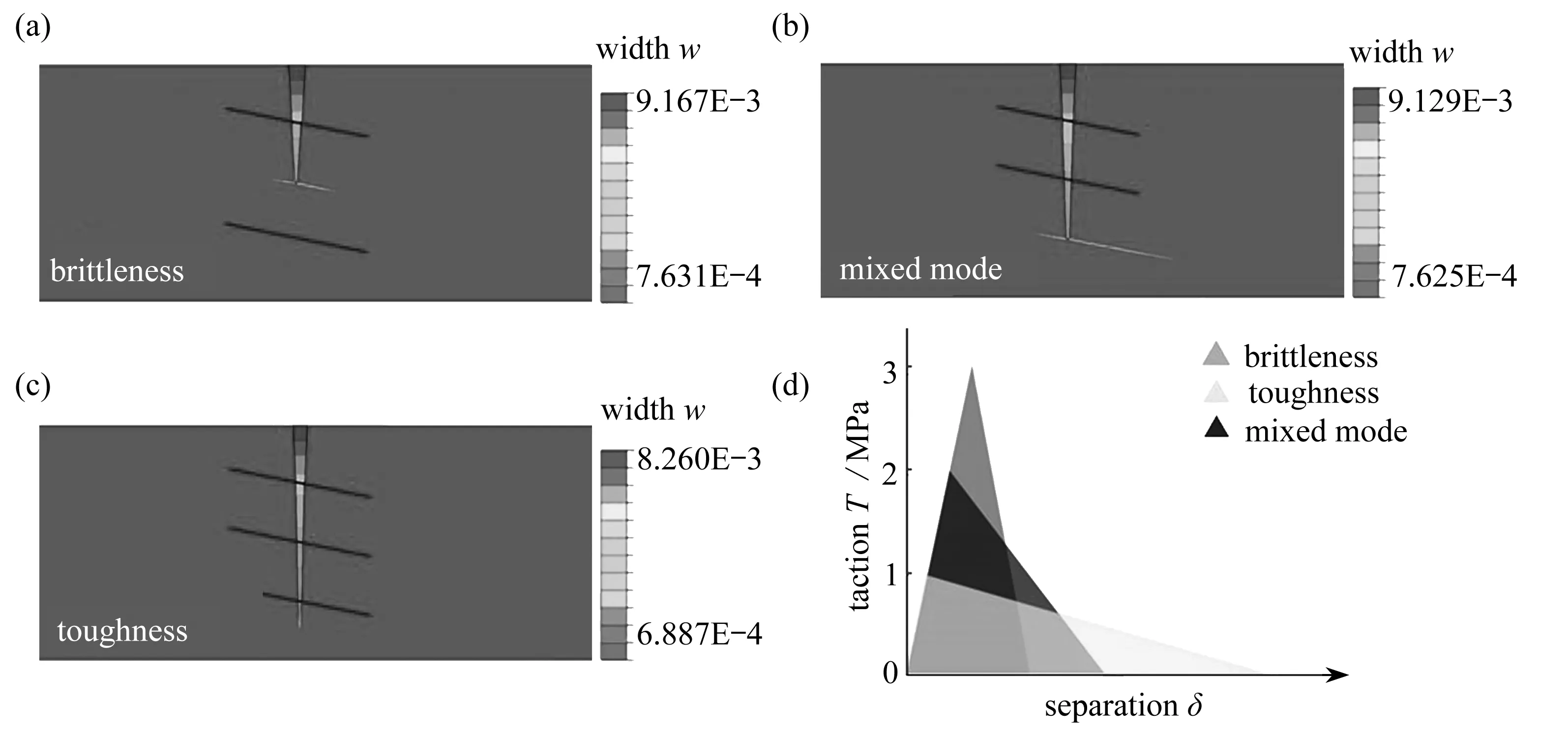
图7 储层和隔层中水力裂缝在不同强度下的断裂机制(方案B)Fig.7 Fracture mechanisms of hydraulic fractures in the pay zone and the barrier at different strengths (plan B)

3.4 压裂参数和岩石材料特性对裂缝形态的影响

页岩中存在大量且随机分布的天然裂缝和层理面,在压裂过程中,它们将与水力裂缝形成不同的交叉角度．为了研究交叉角度对水力裂缝几何形状的影响,我们模拟三种交叉角度的情况,即90°,80°,60°,天然裂缝与层理面是平行且间隔相等的．图8给出了不同交叉角度下裂缝扩展形态的变化．可以看出,随着交叉角度的减小,水力裂缝扩展方向发生偏转,更容易沿着天然裂缝或层理面扩展．这是由于交叉角度减小,垂直于天然裂缝或层理面上的应力减小,天然裂缝或层理面更容易被开启．

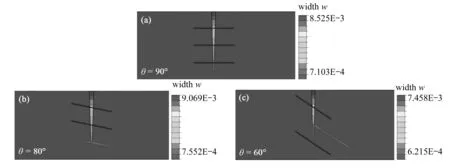
图8 裂缝形态随水力裂缝与层理面的交叉角度的变化Fig.8 Variations of the fracture morphology with the approaching angle between the hydraulic fracture and the bedding plane

地应力差是影响水力裂缝与天然弱界面相互作用的主要因素之一．储层的最小水平主应力不变,依次改变隔层最小水平主应力为5 MPa,6 MPa,7 MPa,三种模拟方案对应的地应力差分别为0 MPa,1 MPa和2 MPa．图9展示了在不同地应力差下,裂缝扩展形态的变化．可以观察到,当地应力差为0 MPa和1 MPa时,水力裂缝贯穿所有的天然裂缝和层理面．当地应力差增到2 MPa时,裂缝沿着隔层的天然裂缝发生偏转．

图9 裂缝扩展随地应力差的变化Fig.9 Variations of the crack extension with the stress difference

层理面胶结强度的高低可以由抗拉强度表示,为研究层理面抗拉强度对水力裂缝扩展的影响,本小节选取三个模拟方案,即层理面的抗拉强度分别为1.5 MPa,2 MPa和2.5 MPa．图10给出了在不同抗拉强度下裂缝扩展形态的变化．可以看出,当层理面的抗拉强度为1.5 MPa时,由于层理面的胶结强度较低,水力裂缝沿着层理面扩展．适当提高层理面的抗拉强度至2 MPa时,裂缝贯穿层理面,最终沿着隔层的天然裂缝发生偏转．当层理面抗拉强度继续增加至2.5 MPa时,水力裂缝贯穿层理面和天然裂缝．这是因为在层理面抗拉强度较高的情况下,层理面难以开启,水力裂缝易直接穿越层理面扩展．

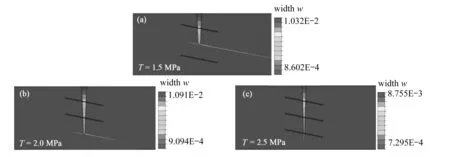
图10 裂缝扩展随层理面抗拉强度的变化Fig.10 Variations of the crack extension with the tensile strength of the bedding plane

在水力压裂过程中,流体的注入速率是重要的施工控制参数之一．为研究注入速率对裂缝扩展形态的影响,本小节选取三个模拟方案,注入速率分别为0.005 m2/s,0.01 m2/s和0.015 m2/s．图11展示了在不同的注入速率下,裂缝扩展形态的变化．可以观察到,当注入速率为0.005 m2/s时,裂缝朝着层理面的方向发生偏转．提高注入速率到0.01 m2/s时,裂缝贯穿层理面,之后沿着隔层的天然裂缝发生偏转．继续增加注入速率至0.015 m2/s时,裂缝贯穿层理面和天然裂缝．图11(d)给出了水力裂缝和开启的天然裂缝的总长度与总注入量的变化曲线．可以看出,在一定的排量下,裂缝的总长度随着注入速率的增加而减小．图11(e)给出了裂缝内的流体压力的变化曲线．可以看出,随着注入速率增加,裂缝内的流体压力相应地增加．

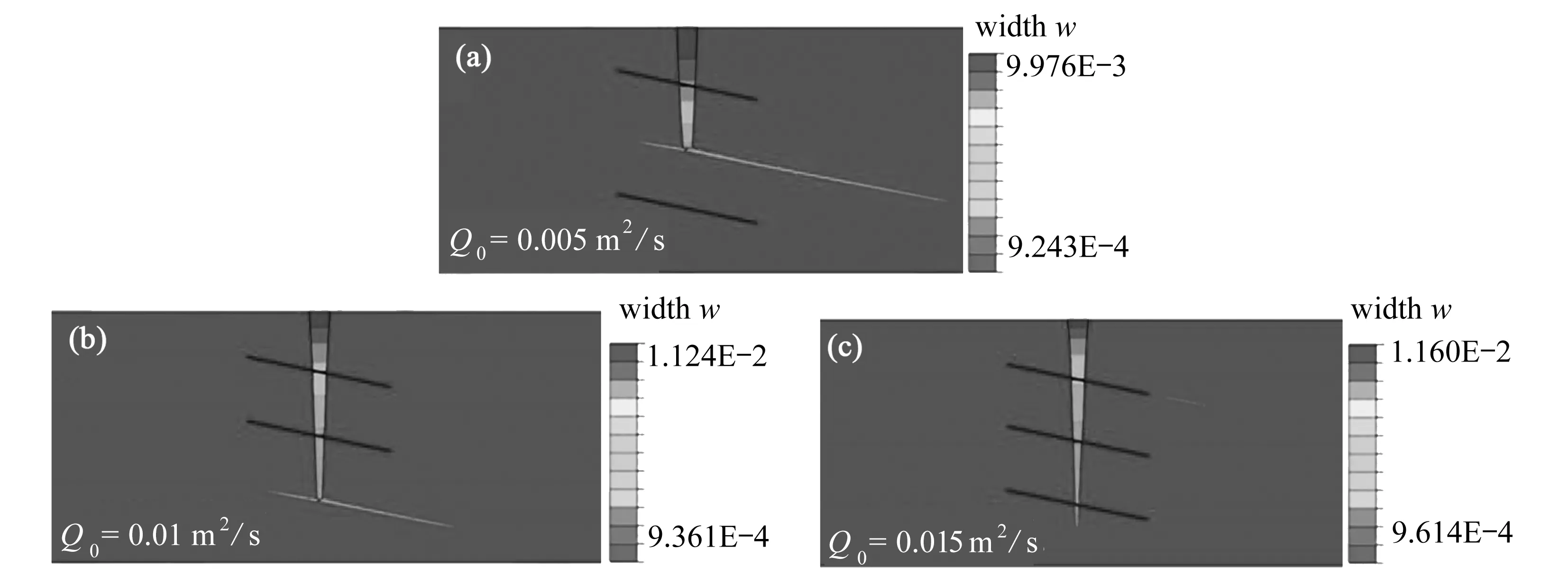
图11 裂缝扩展随注入速率的变化Fig.11 Variations of the fracture extension with the injection rate

本小节研究了在不同交叉角度(水力裂缝与层理面之间的角度)与地应力差作用下,水力裂缝与天然弱界面的相互作用模式．交叉角度取50°到90°的范围与地应力差取0 MPa到2 MPa之间的数值．数值模拟的结果如图12所示．可以看出,随交叉角度的增加,水力裂缝与天然弱界面的相互作用模式发生转变．交叉角度较小时,水力裂缝会被天然弱界面捕获,进而改变水力裂缝的扩展方向．交叉角度较大时,水力裂缝表现为贯穿天然弱界面．根据本文的数值计算结果,在贯穿和连通天然弱界面交界处通过三个数值点拟合出一条曲线y=7.486 1ln(x)-31.31,并通过预测点验证拟合的曲线．在曲线的左侧,水力裂缝表现为连通天然弱界面;而在曲线的右侧,水力裂缝表现为贯穿天然弱界面．预测的点能够进一步验证拟合曲线的准确性．

图12 分层页岩中交叉角度-地应力差的散点图Fig.12 The scatter plot of the stress difference vs.the approaching angle in the layered shale

4 结 论

本文基于有限元方法和自编UMAT子程序,建立了一个二维的弹塑性模型,研究了天然弱界面对水力裂缝扩展形态的影响．数值模型得到了KGD模型和Blanton曲线的验证．研究结果表明:与线弹性的数值模型相比,在考虑岩石塑性变形的模型中,水力裂缝更容易沿着天然弱界面扩展;压裂过程中裂缝尖端附近形成明显的塑性变形,随着时间的增加,裂缝向前扩展,裂缝的周围形成一定厚度的塑性区,塑性区域主要集中在储层内;储层或隔层的岩石发生脆性破坏时,水力裂缝倾向于沿着层理面扩展,而发生韧性破坏时,裂缝倾向于贯穿层理面;在高的注入速率下,裂缝内的流体压力升高,水力裂缝更容易贯穿天然弱界面．在一定的排量下,裂缝的总长度随注入速率的增加而减少．根据计算的结果,本文拟合了一条关于储层和隔层的最小水平地应力差与水力裂缝和层理面之间的交叉角度的数值曲线y=7.486 1ln(x)-31.31,用于判断水力裂缝贯穿天然弱界面的情况,预测的结果和数值模拟具有很好的一致性．