带Caputo导数的变分数阶随机微分方程的Euler-Maruyama方法

刘家惠, 邵林馨, 黄健飞

(扬州大学 数学科学学院,江苏 扬州 225002)

0 引 言

分数阶微积分理论是数学的一个重要分支,是一门研究任意阶导数和积分的学科．在初始阶段的发展过程中,它被认为是一个抽象的数学概念[1],几乎没有任何应用的空间．但是,随着研究的深入,现如今它被认为是科学界进行数学建模最重要的工具之一[2-5]．科学工程的各种重要现象都可以用它来很好地描述,包括部分推移物质输运扩散模型、地震动力学、黏弹性系统、生物物理系统、混沌和波传播等,并且已经较广泛地用于模拟控制理论研究、聚合物研究、信号和图像处理系统、计算机网络、数学生物学等领域[6-10]．

分数阶微积分理论应用的日渐增加推动了分数阶微分方程数值解法的发展和研究[11-13]．因为其中有不确定性因素的存在,所以大多数分数阶随机微分方程的精确解很难求得,只能提供解的数值逼近,如文献[14]中,Jing等研究了一类由分数阶噪声驱动的分数阶随机偏微分方程的平均原理,发现在某种条件下,该分数阶随机偏微分方程的解可以由平均随机系统的解来近似表示;在文献[15]中,Guo等施加了一些新的平均条件来处理Caputo分数阶随机微分方程的平均原则,研究发现:Caputo分数阶随机微分系统的解可以被相应的均值方程的解所逼近．由于Euler-Maruyama(EM)方法具有简单的代数结构、廉价的计算成本和在全局Lipschitz条件下可接受的收敛速度[16-17],因此它一直吸引着大量学者的注意力,如在文献[18]中,钱思颖等用EM方法求解了一类带有弱奇性核的多项分数阶非线性随机微分方程．

变分数阶随机微分方程的研究是分数阶随机微分方程领域的新课题,因为它具有变化的阶数,可对黏弹性行为进行长时间的建模[19]．本文将采用并扩展文献[20]中的理论分析方法来研究以下带Caputo导数的变分数阶随机微分方程的适定性问题及其EM方法:

(1)

本文的第1节将介绍文中用到的基本定理、基本引理和相关假设;第2节将对该变分数阶随机微分方程进行转化并探索解的存在性、唯一性和连续依赖性;第3节将推导出该变分数阶随机微分方程的EM方法,并证明其强收敛性;第4节将进行数值实验来验证理论分析结果;第5节将给出本文的总结．

1 预 备 知 识

1.1 基本知识

定义1 设f:[0,+∞)→,则称

为α(t)阶的分数阶Riemann-Liouville积分[21],其中α(t)>0,Γ(·)为Gamma函数．

定义2 设函数f∈C[0,+∞),0.5<β<1,则称

为β阶的分数阶Caputo导数[22-24]．

1.2 假设条件

假设1f(t,y)和g(t,y)在上满足Lipschitz连续,存在L>0对所有x,y∈,t∈[0,T]都有

|f(t,x)-f(t,y)|∨|g(t,x)-g(t,y)|≤L|x-y|．

假设2f(t,y)和g(t,y)在 [0,T]上满足Lipschitz连续,存在L>0使得对所有x∈,t,s∈[0,T]都有

|f(t,x)-f(s,x)|∨|g(t,x)-g(s,x) |≤L|t-s|．

假设3(线性增长条件) 存在常数L>0对所有的x∈,t∈[0,T],有

|f(t,x)|∨|g(t,x)|≤L(1+|x|)．

假设4α(t)在区间 [0,T]上连续可微,0.5<β<1,且存在0<α(t)<α*<β<1,对任意的0≤α(t)≤1,都有α*+α(t)>1．

2 变分数阶随机微分方程解的适定性

2.1 方程的等价变形

对式(1)的两边同时作用Riemann-Liouville积分算子:

可以得到

(2)

其中

变换上面累次积分的次序,可以得到

令

(3)

则式(2)可写成

(4)

2.2 解的适定性

本小节将采用文献[25]中的技巧来证明方程(1)的解的适定性,即解的存在性、唯一性和连续依赖性．设G2([0,T])为所有可测过程X的空间,其中X是FT适应的,FT={Ft}t∈[0,T],且满足

显然,(G2([0,T]),|·|G2)是一个Banach空间．引入算子Zγ,即

(5)

其中,等号右边的第一个积分本质上是一个双重积分．为了利用算子Zγ来证明方程(1) 的解的适定性,首先将验证算子Zγ的合理性．

引理1 对于算子Zγ,若f(·,0)是L2可积的和g(·,0)是本性有界的．则当t∈[0,T]时,有下式成立:

E[|Zγu(t)|2]<∞,

即说明算子Zγ定义合理．

证明对式(5)两边的平方求期望,可得

(6)

首先对式(6)右侧第2项进行处理,先对k(t,s)进行放缩．显然,Γ(t)在(0,1]上递减,所以Γ(α(τ))>Γ(1)=1,则有

A(t-s)β-α*,

(7)

其中

(8)

将式(7)代入式(6)右侧的第2项,并使用Hölder不等式[26],则有

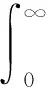
下面处理式(6)右侧的第4项．由于g(·,0)是本性有界的,即有|g(·,0)|∞=supt∈[0,∞)|g(s,0)|<∞．根据It等距定理[27]可得

综上,对于式(6)有

E[|Zγu(t)|2]<∞．

从而引理1得证,即算子Zγ的定义是合理的．下面证明解的适定性．为了证明解的存在唯一性,先在空间G2([0,T])上定义范数|·|λ,即对所有可测过程X,

其中E2β-1(·)是Mittag-Leffler函数[28]．显然,|·|G2和|·|λ是等价的,故(G2([0,T]),|·|λ)也是一个Banach空间．下面来证明算子Zγ在范数|·|λ下是G2([0,T])上的压缩映射[29]．

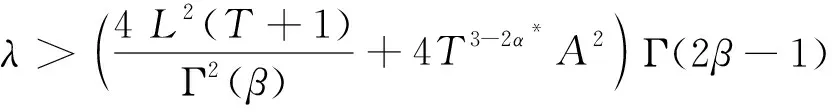
(9)

其中

(10)

(11)

根据Hölder不等式,可得式(11)右侧第1项:

根据Hölder不等式和假设3(线性增长条件),可得式(11)右侧第2项:

综上,式(11)可变为

根据文献[25]的引理5,可得

从而,算子Zγ在(G2([0,T]),|·|λ)上是一个压缩映射,利用Banach空间的不动点定理,方程(1)存在唯一解．

下面证明方程(1)的解对初值的连续依赖性．

定理2 对于T>0,设γ,ξ是方程(1)不同的初值,则有

证明

根据|·|λ的定义以及E2β-1(λt2β-1)≥1得

由文献[25]中的引理5,可得

从而,根据λ的范围有

因此

3 EM方法及其强收敛性

3.1 EM方法的推导

在区间[0,T]上,定义均匀网格的步长h=T/N,在网格节点tn=nh处对式(4)等号右侧的积分项进行离散．

先对式(4)右边第2项的积分采用左矩形法进行离散:

(12)

接下来对第3项的积分项进行离散:

(13)

下面对第4项的积分项进行离散:

(14)

其中ΔWj=Wtj+1-Wtj～N(0,h)．将式(12)—(14)代入式(4),则当1≤n≤N时,有如下EM方法:

(15)

3.2 EM方法解的有界性

定理3 对于1≤n≤N,EM方法的解vn满足如下估计:

(16)

其中

M1=A1[1+Eβ-α*+1(A2Γ(β-α*+1))],

证明

(17)

使用Cauchy不等式和假设3(线性增长条件)处理式(17)右边的第3项,可以得到

(18)

下面处理式(17)右边的第4项,根据ΔWj的独立性和假设3(线性增长条件)可得

(19)

最后,使用微分中值定理计算式(17)右边第2项的估计值,可以得到

再根据式(7)与式(12)可以推出

(20)

将化简后的式(18)—(20)代入式(17),可得

其中,A1,A2的值见式(16)．根据Gronwall不等式[30],定理3得证．

3.3 EM方法的连续形式

(21)

引理2 设{vn}是EM方法的解,v是式(21)定义的时间连续随机过程．那么,当0≤n≤N时,有v(tn)=vn．

证明显然,v(0)=γ=v0．假设当0≤m≤n-1≤N-1时,v(tm)=vm．则

通过数学归纳法,引理2得证．

3.4 连续形式的收敛性

引理3 当0≤n≤N-1时,对任意t∈[tn,tn+1),式(21)中定义的随机过程v都有以下性质:

其中

(22)

证明

通过Hölder不等式对第2项进行放缩:

(23)

基于文献[18]中引理2的估计式,即有

(24)

其中,C为一非负常数．然后,结合假设3(线性增长条件)对第3项进行放缩:

(25)

根据假设3(线性增长条件)以及式(24)对第4项进行放缩:

(26)

最后,根据式(3)对第1项进行放缩:

6M1A2h2(β-α*+1)．

(27)

将式(23)、(25)—(27)代入式(21),可以得到

M2h2(β-α*+1)+M3hβ+1+M4h2β-1,

其中M2,M3和M4的值见式(22),故引理3得证．

3.5 强收敛性误差估计

定理4 设u是式(4)的解,v是EM方法连续形式即式(21)的解,记

M5=A3E2β-1A4Γ(2β-1)T2β-1M2,M6=A3E2β-1A4Γ(2β-1)T2β-1M3,

M7=A3E2β-1A4Γ(2β-1)T2β-1M4,

其中

(28)

则有

(29)

同时,关于EM方法的强收敛性误差估计也成立,即

(30)

证明对任意t∈[0,T),设t∈[tn,tn+1),0≤n≤N-1．根据式(4)与式(21)可得

(31)

结合引理3的证明过程中对各项的放缩结果,对上式右侧三项进行处理,可得

故式(31)可整理为

其中A3和A4的值见式(28)．根据广义的Gronwall不等式,定理4中的式(29)得证．若令式(29)中的t=tn,根据引理2的结论,则可知式(30)成立．

注1 根据定理4中的式(30),由于(β+1)/2 >β-0.5;β-α*+1 >β-0.5,所以EM方法(15)的强收敛阶是β-0.5．

4 数 值 算 例

在本节中,我们将引入数值算例来验证EM方法(15)的强收敛阶．首先,给出误差的计算方法:

其中u(tn,ωj)是方程(1)的第j条样本轨道在tn处的真实解,vn(ωj)是对应的EM方法(15)得出的数值解,收敛阶由κ=log2(eh/eh/2)计算获得．在具体数值实验中,设时间区间[0,T]=[0,1],轨道总数M=1 000,以网格数N=512时的数值解近似表示精确解,规定变分数阶α(t)=α1t+α2．

例1 我们考虑令方程(1)中f(t,u)=g(t,u)=cos(u),初值γ=0.1．首先令Caputo分数阶导数的阶β=0.9,此时的计算误差和收敛阶见表1．

表1 β=0.9时,EM方法的误差与收敛阶Table 1 Errors and convergence orders of the EM method for β=0.9

从表1可以看出,随着步长h的减小,其数值解的误差也在不断减小,且其EM方法的收敛阶接近于β-0.5=0.4,这与定理4的结论相符．

然后,令Caputo分数阶导数的阶β=0.8,计算误差和收敛阶见表2．

表2 β=0.8时,EM方法的误差与收敛阶Table 2 Errors and convergence orders of the EM method for β=0.8

根据表2可以看出,随着步长h的减小,其数值解的误差也在逐渐减小,且其EM方法的收敛阶接近于β-0.5=0.3,与定理4的结论相符,说明了定理4结论的正确性．

最后,令Caputo分数阶导数的阶β=0.7,计算误差和收敛阶见表3．

表3 β=0.7时,EM方法的误差与收敛阶Table 3 Errors and convergence orders of the EM method for β=0.7

由表3可以看出,EM方法的收敛阶接近于β-0.5=0.2,再次验证了定理4结论的正确性．

5 总 结

本文首先讨论了变分数阶随机微分方程解的适定性,并构造了其EM方法,然后证明了EM方法的强收敛性,并得到其收敛阶为β-0.5．最后通过3组数值实验验证了该EM方法计算的有效性,并验证了其理论分析结果的正确性．值得一提的是,本文给出的EM方法及理论分析框架可以拓展到向量值的变分数阶随机微分方程．