低Weissenberg数黏弹性流体中单气泡上浮运动特性研究

张仕环, 庞明军, 郑智颖

(1.常州大学 机械与轨道交通学院,江苏 常州 213164;2.哈尔滨工业大学 能源科学与工程学院,哈尔滨 150001)

0 引 言

气液两相流广泛存在于自然界和工业过程中,如血液中的气泡运动[1],石油输送过程和鼓泡塔内的气泡上浮运动等[2]．气泡的存在会对液相的运动、传热传质和表观黏度等特性产生显著的影响[3]．因此,研究液相中气泡的运动特性对工农业生产和日常生活具有重要意义．工业过程涉及的液相多为非Newton流体,而黏弹性流体又是一种典型的非Newton流体,因此研究黏弹性流体中的气泡运动特性意义重大．

为了理解气泡在非Newton流体中的水动力学特性,前人已经开展了大量的研究[4-19],但关于气泡在黏弹性流体中水动力学特性的研究相对较少．特别是国内学者仅开展了为数不多的实验研究[20-22],理论和数值研究鲜见报道．国外学者Astarita和Apuzzo[23]开创性的实验发现,在黏弹性流体中,当气泡体积大到一定程度时,其上浮速度会突然增大(所谓的“速度不连续性阶跃”),气泡形状呈现为倒置的泪滴状．Hassager[24]实验发现气泡在黏弹性流体内上浮时,其中心尾迹出现了向下流动(即“负尾迹”)的现象,与钢球在黏弹性流体中下沉时的流线形状相似[25]．此后,一些学者实验再现了黏弹性流体中气泡上浮的典型特征[26-30]．

在数值研究方面,Wagner等[31]使用格子Boltzmann方法研究了黏弹性流体中二维气泡的上浮运动,再现了实验中发现的带尖尾部．Pillapakkam等[32]使用水平集方法(level set method),研究了三维气泡在黏弹性Oldroyd-B液体中的上浮运动,再现了上浮速度不连续阶跃的现象．Fraggedakis等[33]基于Phan-Thien Tanner(PTT)黏弹性模型,使用任意Lagrange-Euler法很好地预测了在达到临界体积时气泡速度突然增加的现象．然而,随着研究者们对强弹性流体的数值计算遇到了数值问题,即高Weissenberg数问题(the high Weissenberg number problem,HWNP),为了解决该问题众多学者进行了深入的研究[34-36]．Yuan等[37]在对构象张量进行对数化处理后,使用流体体积(VOF)法研究了高Weissenberg数下气泡在黏弹性流体中的上浮运动特性．Ohta等[38]基于剪切稀化Carreau模型和FENE-CR黏弹性模型考虑流体的剪切稀化和黏弹性特征,使用水平集和流体体积耦合方法(CLVOF)研究了具有剪切稀化特征黏弹性流体中气泡的上浮运动．

综上所述,尽管国内外学者针对黏弹性流体中气泡的上浮运动特性开展了一定的研究,并得到了一些有价值的结论,但相关现象的机理解释仍难以定论．再加上黏弹性流体自身的复杂特性,研究难度相对较大,国内关于这方面的理论和数值研究鲜见报道．特别是当Weissenberg数太大时,开展黏弹性流体的数值计算会遇到“高Weissenberg数问题”,即构象张量分量呈指数增长会导致计算的不稳定性．在实际工业应用中,也经常会遇到弹性较弱(Weissenberg数较小)的黏性流体,比如低分子量(短链)或低浓度的聚合物溶液．为了理解气泡在黏弹性流体中的上浮运动特性,使用数值模拟方法尝试研究了低Weissenberg数下松弛时间、黏性力、表面张力和黏度比对气泡上浮运动特性的影响,详细分析了气泡形状、上浮速度、尾涡和弹性应力的分布特征,为后续深入研究奠定基础．

1 物理问题和计算模型

1.1 几何模型

目前公开发表的数值研究气泡在Oldroyd-B黏弹性流体运动的文献中[32,37],气泡形状基本是左右对称的(除了非稳态工况外),且影响气泡形状的因素基本位于气泡轮廓平面内．本文通过研究低Weissenberg数下,黏性力、松弛时间、表面张力和黏度比对气泡形状的影响来反应气泡上浮时的运动特性,所以将计算域简化为二维平面时,气泡的形状基本不会受到太大影响．尽管对于二维平面假设,圆形气泡不是真实的球形气泡而是一个圆柱体,导致气泡尾流和上升阻力存在一定的偏差,但总体上二维平面计算能定性地反映一定的流动特征[39-41]．而且目前的计算是在低Weissenberg数下进行的,气泡上浮速度相对较小,在一定程度上能将流动失真降低到可接受范围内．另外,目前二维的计算结果,比如气泡形状、速度以及流场信息与文献基本吻合[37]．所以目前二维计算的假设是合理的,既能极大地减小计算成本,又能较全面地研究不同参数对气泡在黏弹性流体中上浮运动的影响．

计算区域设置为一矩形区域,如图1所示．矩形区域内充满黏弹性流体,初始半径R=2.5 mm的圆形气泡受浮力作用从底部自由上浮．为了消除壁面的影响,以及能使气泡运动取得充分发展,矩形区域的高和宽分别取H=90R和W=30R,目前计算区域的尺寸远大于文献[37]的尺寸．气泡距底壁的距离为h=5R,以消除底部壁面对气泡初始运动的影响．

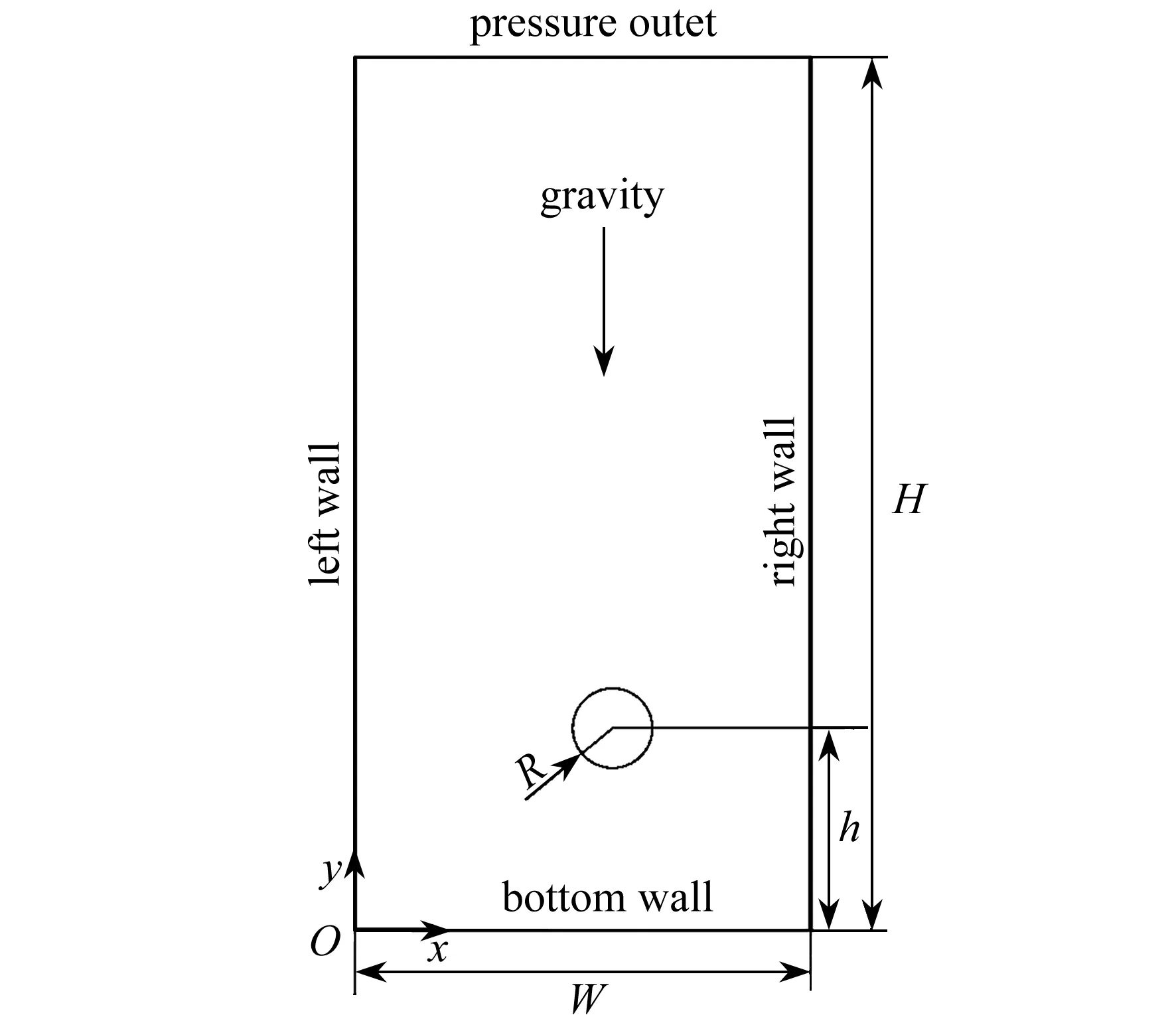
图1 计算模型Fig.1 The computation model

1.2 控制方程

目前的计算是在层流、恒温且气液两相均不可压缩的前提下进行的,流体的控制方程有连续性方程和动量方程,具体如下:

∇·u=0,

(1)

(2)

式中u为速度(m/s),p为压力(Pa),ρ为流体平均密度(kg/m3),t为时间(s),Ds为黏性应力张量,Dp为弹性应力张量,Fs为表面张力源项,g为重力加速度(m/s2)．Ds和Dp的表达式如下:

(3)

(4)

式中μ为流体平均黏度(kg/(m·s)),μp为聚合物的黏度(kg/(m·s)),Cij为柔性高分子聚合物或表面活性剂分子的构象张量,xi为坐标(m),λ为聚合物松弛时间(s),δij为Kronecker符号(i=j时值为1,否则值为0),f(r)为Perterlin函数,即

(5)

(6)

式中L为聚合物分子拉伸长度与平衡长度之比,r为聚合物分子的理想长度．

构象张量Cij的输运方程为

(7)

(8)

1.3 界面捕捉方法

使用VOF法捕捉气液相间的界面,VOF法适用于两种或多种互不相容的流体,通过引入一个或多个体积分数变量来区分各相,在每个控制体中,所有相的体积分数之和为1．当计算区域的位置与体积分数已知时,流体的热物性参数表示为所有相的体积平均值．流场中相分布可以用相函数F表示,其被定义如下:

(9)

流体平均密度ρ和黏度μ均是气液相的体积分数平均值,即

ρ=ρL(F)+ρG(1-F),

(10)

μ=μL(F)+μG(1-F),

(11)

式中ρL为液相的密度(kg/m3),ρG为气相的密度(kg/m3),μL(=μs+μp)为液相的黏度(kg/(m·s)),μG为气相的黏度(kg/(m·s)),μs为溶剂的黏度(kg/(m·s)),μp为聚合物的黏度(kg/(m·s))．

VOF法通过求解体积分数(或相函数)输运方程来跟踪界面,方程如下:

(12)

界面采用Youngs[42]提出的分段线性法(PLIC)进行重构,重构后的界面不是连续的．因此为了保证计算精度,对网格大小有严格的要求．

1.4 表面张力模型

表面张力采用Brackbill 等[43]提出的连续表面力模型(CSF)计算,气泡表面的力可以用散度定理表示为体积力,将体积力作为源项加入动量方程(2)中,源项Fs表示为

(13)

(14)

1.5 边界条件和数值方法

在图1所示的矩形计算区域中,上壁面设置为压力出口边界条件,左、右和下壁面均设置为无滑移壁面．由于结构化网格具有网格质量好、数据结构简单且容易实现区域边界拟合等优点,所以采用结构化网格对整个计算区域进行网格均匀划分．梯度项使用基于网格中心的最小二乘法进行离散;动量方程采用二阶迎风格式进行离散;压力项采用PRESTO! (pressure staggering option)方法离散;体积分数采用几何重构法求解．时间上的推进采用一阶隐式格式,压力和速度场的耦合选用SIMPLE算法．当气泡形状和上浮速度基本不随时间变化时,计算视为收敛．所有参数设置完成后进行混合初始化,然后在计算域中加入气泡,开始两相流的计算．

1.6 计算条件和工况设置

为了研究气泡在黏弹性流体中的上浮特性,控制液气密度比为ρL/ρG=1 000和液气黏度比为μL/μG=100,分别研究了Galileo数(Ga)、Weissenberg数(Wi)、Eotvos数(Eo)和黏度比(β)对气泡运动的影响．Wi表征聚合物松弛时间与对流时间尺度的比值,Ga表征重力与黏性力的比值,Eo表征重力与表面张力的比值,β是溶剂和溶液的黏度比,分别定义如下:

(15)

表1 计算工况Table 1 Design of the computation case

2 结果分析和讨论

2.1 网格尺寸与时间步长的确定

2.2 结果可靠性验证

为了确保计算的可靠性,本文将参数为Ga=1.95,Eo=1,Wi=1和β=0.8时的计算结果与文献[37]的结果进行了对比．图4(左侧为当前结果,右侧为文献[37]结果)对比了气泡的形状,可以看出气泡形状高度吻合．图5对比了气泡的上浮速度,时间和速度按照文献[37]进行了无量纲化处理(t*=t/(R/Ug)和v*=v/Ug)．从图中看出,气泡稳定后的上浮速度分布基本一致,加速阶段存在轻微的差异,或许是因以下原因造成的:① 本文使用的是二维模型,文献使用的是三维模型;② 文献对构象张量进行了对数化处理以处理高Weissenberg数带来的数值问题．总而言之,目前的计算方法是可信的,可以开展目前的研究工作．

图4 气泡形状对比 图5 气泡上浮速度对比Fig.4 Comparison of bubble shapes Fig.5 Comparison of bubble center velocities

2.3 气泡变形分析

气泡形状会直接影响周围液相流场的分布,进而对相间的传质传热效率产生影响．为此,首先分析了各参数对黏弹性流体中上浮气泡形状的影响．图6给出了黏度比β=0.2时,气泡上浮运动稳定后的形状．对应不同的参数,气泡呈现为圆形、椭圆形、帽形(破碎和未破碎)、倒置泪滴状以及其他不规则形状．随着Ga数的增大,气泡从圆形向帽形转变,并逐渐趋于扁平状．当Ga=2,在低Wi数和低Eo数时,气泡保持为圆形;当Eo数增大时,由于表面张力的减小,气泡底部受向上射流的影响发生了轻微的上凹;当Wi≥0.5时,气泡在低Eo数下,圆形气泡底部在弹性力的拉伸作用下变长,随着Eo数的变大,气泡下部形成一个带尖的尾部(所谓的“尾缘尖”),最终呈现为倒置的泪滴状．当Ga=4时,气泡形状总体变得扁平(与Ga=2时相比),而且高Wi数下的“尾缘尖”现象消失;在较大Eo数下,出现了帽形气泡．随着Ga数的进一步增大,当Ga=8时,气泡变得更加扁平;且在Eo=100时,气泡底部出现了破碎现象,形成了许多卫星气泡．当Ga=16,在Eo=1时,出现了非稳态气泡,气泡呈不规则形状,上浮路径为“之”字形;随着Eo数的增大,气泡破碎加剧．Wi数的大小表征了液体黏性和弹性的相对强弱．对于目前的研究,当Wi=0.1时,液相的弹性相对较弱,气泡变形与在纯黏液体中的变形相似．随着Wi数的增大,液相的弹性增强,因此气泡受液相弹性应力的影响变得明显,当Ga=2时,气泡形状呈现出尾缘尖特征．随着Eo数的增大,即表面张力的减小,气泡保持原有形状的能力变弱,气泡形状从椭圆形向尾部破碎的帽形转变．

(a) Wi=0.1 (b) Wi=0.5 (c) Wi=1图6 β=0.2时,气泡形状随Ga数,Wi数和Eo数的变化Fig.6 Bubble shapes against Ga,Wi and Eo numbers at β=0.2

为了理解黏度比对气泡形状的影响,图7给出了Eo=10时,黏度比β=0.2,0.5,0.8下,气泡形状随Ga数和Wi数的变化．结合图6可以看出,随着黏度比β的增大,原本出现“尾缘尖”的工况,气泡变形为帽形．这是因为随着黏度比β的增大,聚合物的黏度变小,液相的弹性变弱而黏性增强,即液相施加在气泡上的黏性力变大而弹性力变小．所以气泡变形与小Wi数的工况相似,类似于在纯黏流体中的变形．

(a) Wi=0.1 (b) Wi=0.5 (c) Wi=1图7 Eo=10时,气泡形状随β,Ga数和Wi数的变化Fig.7 Bubble shapes against β,Ga and Wi numbers at Eo=10

为了理解气泡在黏弹性流体中出现的“尾缘尖”现象,给出聚合分子与气泡作用示意图(图8)．气泡受浮力作用向上运动时,由于黏性的影响会拖动气泡周围的液体一起向上运动,表征液相弹性的聚合物分子会受到拉伸．当聚合物分子被拉伸到一定程度时,会恢复至平衡态(类似于弹簧),这时液相中会产生一个与气泡运动相反的力,也就是所谓的弹性应力．当弹性应力足够大时,会通过黏性作用将力施加到气泡表面上,该力最终作用在气泡底部正中间,所以该区域受拉力的作用变形最明显,形成“尾缘尖”．

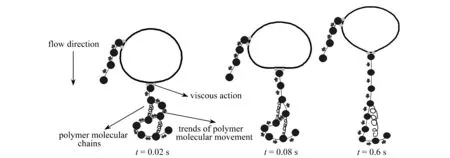
图8 Wi=1和Ga=2时,聚合物分子对气泡变形的影响Fig.8 Schematic of effects of polymer molecules on bubble deformation at Wi=1 and Ga=2

另外,对于Eo=1和Ga=16所有的工况,气泡形状和运动均极不规则(所谓的非稳态气泡),气泡沿“之”字形路径上浮．这是因气泡两侧尾涡周期性的脱落,在气泡左右两侧产生了周期性的升力引起的．文献[18,43-44]的实验研究也发现了类似的现象．

2.4 气泡上浮速度分析

气泡的上浮速度(指气泡内所有节点的平均速度)是研究气泡水动力学的一个重要参数,气泡的上浮速度在一定程度上影响了液相的含气率,含气率的高低会影响液相的表观黏度和相间的传递效率[45-46],所以研究气泡的上浮速度非常必要．为了研究弹性力和表面张力对气泡上浮速度的影响,图9给出了Wi数和Eo数对气泡上浮速度的影响．从图中可以看出,当Eo=1时,随着Wi数的增大,气泡上浮速度随之增大．对应图6给出的气泡形状可知,上浮速度增大的原因可能是在弹性应力作用下,气泡下半部分受到拉伸,气泡尾部变尖,气泡整体形状更接近于流线型,边界层不易分离,气泡上升过程受到的形状阻力较小．当Eo=10和100时,Wi数对气泡上浮速度的影响不明显,这是因为气泡形状均呈现为帽形,横向尺寸相似,所以气泡受到的形状阻力也相似,导致上浮速度变化不大．另外,在相同的Wi数下,随着Eo数的增加,气泡上浮速度先快速减小,然后缓慢减小．这是由于气泡的形状先由圆形变为帽形、最终近似稳定为帽形,导致阻力先快速增大然后趋于稳定引起的．

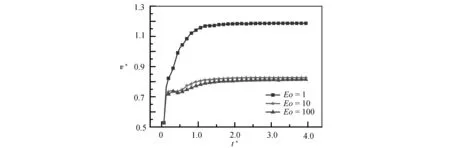
(a) Wi=1

(b) Wi=0.5 (c) Wi=0.1图9 Ga=4和β=0.2时,Wi数和Eo数对气泡上浮速度的影响Fig.9 Effects of Wi and Eo numbers on the bubble rise velocity at Ga=4 and β=0.2

图10给出Ga数对气泡上浮速度的影响(Eo=10,β=0.2)．当Wi=0.1和0.5时,随着Ga数的增大,稳定后气泡的上浮速度随之增大．这是由于随着Ga数的增大,在重力保持不变的情况下,气泡受到液相的黏性阻力减小引起的．在较大的Ga数(Ga=16)下,由于气泡前一时刻的破碎,导致气泡上浮速度在稳定前出现了一个峰值．当Ga数较小(如Ga=2)时,气泡上浮速度随Wi数的变化表现出一定的差异．当Wi=1时,气泡经历了一个“加速-减速-再加速”的过程,最后气泡上浮速度超过相同工况下黏度较小(即Ga数较大)的工况．第一阶段气泡的加速是因浮力作用引起的;第二阶段的减速是因气泡底部受到射流的作用、发生上凹变形,变形成帽形,气泡的形状阻力增大,所以出现了减速现象;第三阶段的加速是因液相中聚合物分子的弹性拉伸,气泡底部受到聚合物恢复至平衡态向下的弹性拉力,气泡从帽形变为“倒置的泪滴”状,形状阻力又减小,所以气泡的上浮速度又增大．因气泡形状最终稳定在阻力最小的状态,所以气泡速度高于低黏度工况下的速度．气泡的变形过程如图8所示．

(a) Wi=1

(b) Wi=0.5 (c) Wi=0.1图10 Eo=10和β=0.2时,Ga数对气泡上浮速度的影响Fig.10 Effects of the Ga number on the bubble rise velocity at Eo=10 and β=0.2

另外,从图9可以看出,当其他条件相同,Eo=1时,气泡上浮过程没出现再加速现象,而是一次性加速达到稳定的峰值;但Eo≥10时,气泡速度出现了轻微的波动．这说明形状阻力的变化是导致气泡出现再次加速的主要原因．Niethammer等[47]报道过类似的现象,他们认为第一阶段气泡的加速是因浮力驱动引起的,这与本文一致,而第二阶段气泡的减速,则被归因于气泡表面弹性应力层足够大以至于对气泡运动产生了影响,对于第三阶段气泡的加速他们认为当气泡体积大于临界体积时,气泡赤道下方的环向弹性应力引起气泡再次大幅加速[48]．

图11展示了黏度比β对气泡上浮速度的影响(Ga=2,Eo=10)．当Wi=1时,随着黏度比的变大,气泡上浮速度明显减小．这是因为黏度比β的增大导致黏性力作用增强而弹性力的作用减小,导致气泡受到的黏性阻力增大,所以上浮速度变小．通过对比图中β=0.2所有的工况可以看出,上文中提到的“加速-减速-再加速”现象随着Wi数的增大而变得明显．这足以说明弹性力对气泡形状和上升速度的影响非常大．

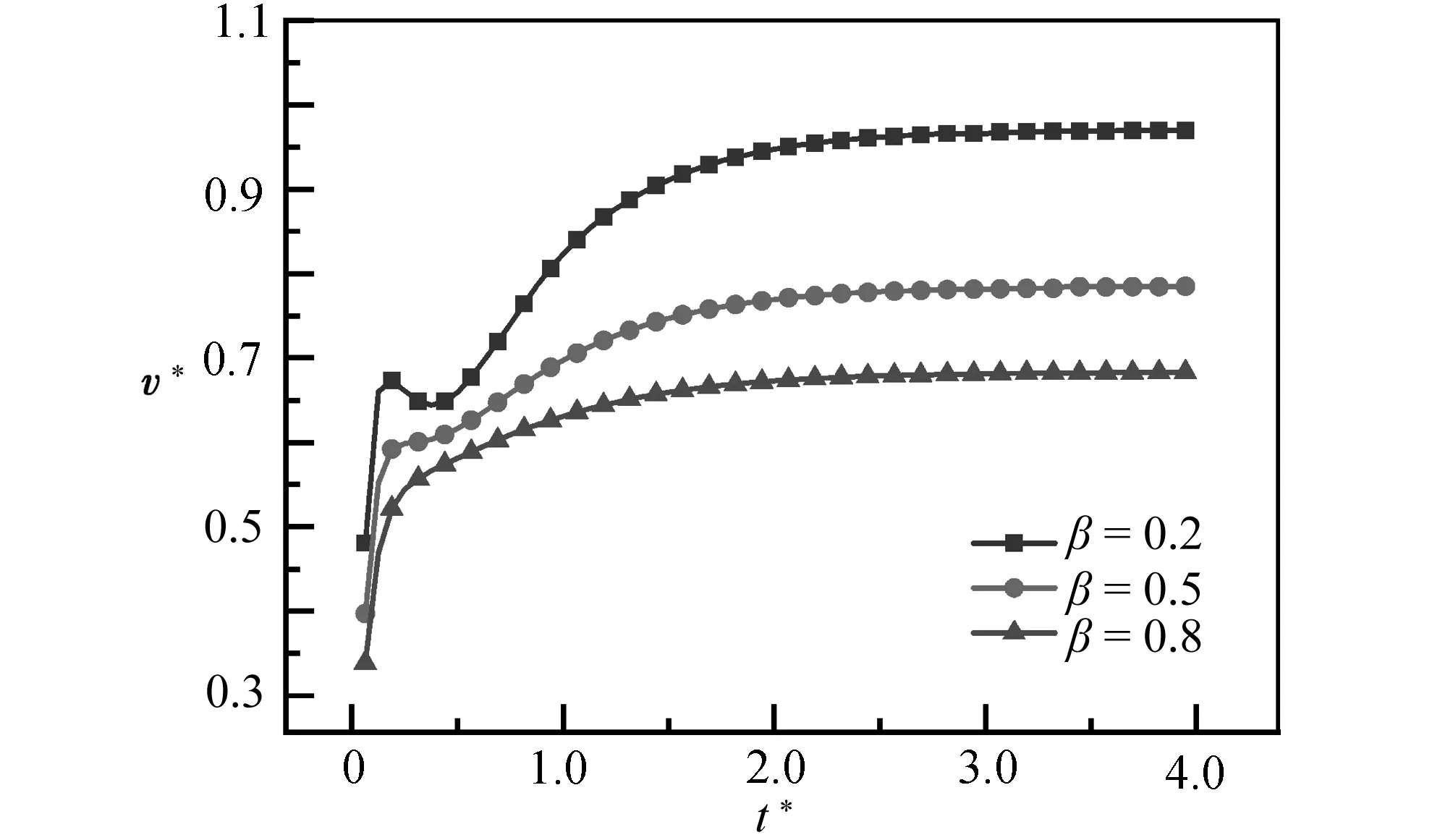
(a) Wi=1

(b) Wi=0.5 (c) Wi=0.1图11 Ga=2和Eo=10时,黏度比β对气泡上浮速度的影响Fig.11 Effects of viscosity ratio β on the bubble rise velocity at Ga=2 and Eo=10

综合对比图9—11可以发现,气泡在黏弹性液体中上浮时,气泡上浮速度随时间的变化表现出现“持续加速到稳定”和“加速-减速-再加速到稳定”两种形式,这不同于气泡在纯黏流体中的现象,说明了弹性的影响非常显著．气泡在纯黏流体中上浮时,普遍会出现“加速-减速-(某些条件下)轻微再加速”,最后取得稳定的终端速度[37],这种速度波动是因浮力和阻力之间的动态平衡引起的．对于黏弹性流体中“持续加速到稳定”现象是因下述原因引起的,即当弹性较弱(Wi=0.1)和表面张力较大(Eo≤10)时,气泡变形轻微,既不会因射流作用尾部迅速上凹,也不会因为弹性力作用呈现“尾缘尖”,此时浮力与气泡阻力之间动态平衡产生的速度波动现象因弹性力的存在变得不明显．当弹性较强(Wi≥0.5,β=0.2),黏度较大(Ga=2)和表面张力较弱(Eo≥10)时,气泡底部出现“尾缘尖”导致形状阻力大幅减小,从而出现了明显的再次加速．第二阶段减速现象仍存在的原因是,当弹性聚合物松弛时间较大时,弹性应力的释放存在一定的延迟,气泡底部受射流的影响仍会存在上凹的历程．

2.5 气泡尾涡分析

为了进一步分析气泡在黏弹性流体中的水动力学特性,下面给出了气泡的尾涡分布图．图中红线表示气泡的边界轮廓．对于所有的工况,气泡内部都形成了两对对称的涡,一对较大,另一对较小．为了理解各参数对气泡尾涡分布的影响,图12给出了Ga=4和β=0.2时,Wi数和Eo数对气泡尾涡的影响;图13给出了Eo=10和β=0.2时,Ga数和Wi数对气泡尾涡的影响．

图12 Ga=4和β=0.2时,Eo数和Wi数对气泡尾流的影响Fig.12 Effects of Eo and Wi numbers on the bubble wake at Ga=4 and β=0.2

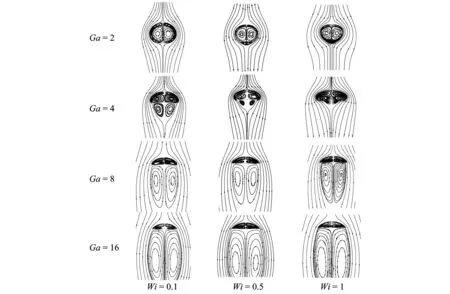
图13 Eo=10和β=0.2时,Ga数和Wi数对气泡尾流的影响Fig.13 Effects of Ga and Wi numbers on the bubble wake at Eo=10 and β=0.2

从图12中可以看出,当Wi数相同,在Eo=1时,由于气泡变形较小,气泡尾部没有尾涡生成．这是因气泡形变小(界面曲率大且变化小),在气泡界面产生的涡量较小,很快被来流带走,不会聚集在气泡尾部．当Eo=10和100时,气泡形变明显、呈现为帽形,界面曲率变化大且流动阻力(主要是形状阻力)使气泡上下侧的压差变大,导致了尾涡的出现,且随着Eo数的变大,尾涡被逐渐拉长．当气泡形变成帽形时,尾涡的出现导致气泡的上浮速度大幅减小．从图13可以看出,当其他参数相同时,随着Ga数的增大气泡尾涡明显增大．随着Wi数的增大,气泡的尾涡尺寸变小,这是因为弹性力在一定程度上能够阻止气泡形变为帽形,减小气泡的形状阻力．这也进一步解释了气泡上浮速度随着Wi数的增大而增大的原因．

2.6 气泡周围正应力分析

因聚合物正应力τyy云图在一定程度上能体现气泡周围聚合物浓度和弹性应力的作用效果,而且通过观察正应力云图可以更直观地理解弹性应力的作用规律．为此,给出了液相的正应力τyy分布云图(图14)．

(a) Wi=0.1 (b) Wi=0.5 (c) Wi=1图14 β=0.2时,τyy分布云图Fig.14 At β=0.2,contour plots of τyy

从图14可以看出,大正应力区主要集中在气泡尾部和气泡赤道位置附近,这些区域也是剪切较强的区域,这也再次证明弹性应力对气泡变形的影响不容忽视．当其他参数相同时,随着Wi数的增大,正应力的大小和作用范围总体上表现出增大的趋势．前文提到弹性应力使气泡尾部受到拉伸,气泡形状趋于流线形,从而导致上浮速度增大．从正应力云图来看,大弹性应力出现在气泡赤道附近,分析对应位置处的流线不难看出,当气泡上浮时,气泡顶部和周围的液体向赤道位置汇聚,导致气泡表面附近存在较大的速度梯度,所以形成较强的剪切作用．受剪切的影响,气泡赤道附近聚合物分子被向下拉伸,从而在气泡上产生一个向上的弹性应力,也可使气泡上浮速度变大,如图8所示．当其他参数相同,改变气泡的Eo数时,气泡的形状随之变化,导致正应力的大小和位置也发生变化．当Eo数较小时,气泡变形较小,大正应力区域主要出现在气泡两侧偏上和尾部区域;当Eo数较大时,气泡变成帽形,大正应力区域逐渐移动到帽形的裙边处;当气泡出现破碎时,大正应力区域分布在脱落气泡的周围,也出现了大应力区域脱落的现象．对于大Ga数的工况,正应力作用区域相对变大,但大应力区域减小．一方面是聚合物黏度减小的原因;另一方面是小黏性力的作用导致气泡上浮速度较大,在聚合物分子松弛时间不变的前提下,在聚合物分子单次拉伸恢复至平衡态所需的时间内,气泡上浮了更远的距离,从而导致正(弹性)应力作用区域变大．

3 结 论

本文基于Oldroyd-B黏弹性模型,运用VOF法模拟了气泡在黏弹性流体中的上浮运动．再现了气泡在黏弹性流体中呈倒置泪滴形状的现象,解释了该现象产生原因,并详细分析了Ga数、Eo数、Wi数和黏度比β对气泡形状和上浮速度的影响．主要结论总结如下:

1) 气泡在黏弹性流体中上浮时,可呈现为圆形、椭圆形、帽形(破碎和未破碎)、倒置泪滴状和其他不规则形状．随着Ga数和Eo数的增大,黏性力和表面张力减小,气泡变形程度增加;在大Wi数和小黏度比β下,弹性较强,气泡底部受到强烈的拉伸作用; 在小Wi数和大黏度比β下,弹性较弱,气泡形状与纯黏流体中的相似．当Ga=16和Eo=1时,气泡受到周期性升力的作用表现出非稳态形状; 当Ga=2,Wi≥0.5和β=0.2时,气泡尾部出现了大小不同的“尾缘尖”,该现象是弹性力、黏性力、表面张力和惯性力综合作用的结果,而弹性力是“尾缘尖”现象的必要条件．

2) 气泡在黏弹性液体中的上浮速度普遍大于在纯黏液体中的速度．与纯黏流体不同,气泡在黏弹性流体中上浮时,气泡上浮速度有持续加速到终端速度和加速-减速-再加速到终端速度两种形式,后者的再加速现象是因气泡“尾缘尖”的出现导致气泡所受形状阻力减小引起的．

3) 当气泡变成帽形时,因气泡上下两侧压差较大且界面曲率变化较大,在气泡尾部出现了尾涡,气泡尾涡随着Eo数的增大而拉长．τyy大应力区主要集中在气泡尾部和赤道处;随着Wi数的增大,聚合物松弛时间变长,且气泡将聚合物分子拉伸长度变大,所以弹性应力作用范围变大．

致谢本文作者衷心感谢常州大学“SIETP”基金项目(2022-C-06)对本文的资助．