基于相似规律和神经网络的多级多相混输泵气液增压性能预测
常 亮, 杨晨宇, 苏筱斌, 戴晓宇, 徐 强, 郭烈锦
(西安交通大学 动力工程多相流国家重点实验室,西安 710049)
0 引 言
多相混输泵是指能够同时对气液固多相流体增压的流体机械装备.作为一种可靠的气液混输增压方法,多相混输泵被广泛应用在许多重要的工业过程中,如深海长距离油气混输、井下油气开采人工举升等[1-2].在油田生产中后期,许多仍有开发潜力的油气井被迫关停.应用井下混输泵有助于降低井口回压、提高油气产量,有效延长油田生命周期[3].在高温井中(>175 ℃),混输增压提高了井筒内液体的沸点,节约了添加抑制剂的高额成本[4].然而,我国深海油气开发技术在总体上仍落后于发达国家,处于领先的高新技术占比率不超过30%,其中60%以上的技术处于跟踪状态[5-6].油气产量与混输泵气液增压特性密切相关,准确预测和评估多相混输泵增压能力对于指导油气生产,改善油气开发经济性至关重要.
混输泵气液增压特性受多个参数影响,如气液流量、入口压力、转速、级数和工质物性等[7-8].不同气液流量下,旋转叶轮内部气液流体在压力梯度力和离心力作用下容易发生相分离,表现为不同的气液流型[9-11].气液流型与混输泵气液增压存在强相关关系,多种流型结构与其转变导致气液增压的准确预测十分困难.Turpin等[12]首先提出了混输泵气液两相扬程的经验预测关联式,并给出了区别稳定和非稳定流动的边界判别式.为了将预测范围向高含气率推广,Duran和Prado[13]提出了针对离散气泡流型和团聚气泡流型的气液增压预测关联式.Furuya[14]采用一维控制体方法根据叶轮内部离散气相和液相的相互作用力建立了动力学模型.当含气率低于20%时,预测最大相对误差为±30%;当含气率高于30%时,最大相对误差为±50%.最近,在前人研究的基础上,Zhu等[15]从Euler理论扬程出发,考虑各项流动损失,建立了泡状流和气团流条件混输泵增压预测模型,对三种离心式混输泵均取得了较好的预测结果,误差在±20%以内.
在长期研究和应用过程中,研究者们基于流体力学相似理论总结提出了水泵相似定律.然而,在油气混输工业现场,工质一般为气液两相或多相流体.Matsushita等[16]采用单级稠密双叶栅叶轮,从叶轮外径、叶片高度和转速三个方面,实验研究了空气-水两相条件下相似规律的适用性.直径为190 mm和235 mm的两种叶轮能较好地符合相似规律,转速为1 000~1 600 r·min-1,气液流量比为0~0.6.司乔瑞等[17]研究发现,在不同转速下(1 800~2 910 r·min-1),当入口含气率低于0.03时,单级蜗壳式离心泵能较好地遵循两相相似规律.Patil和Morrison[18]采用流量系数和旋转Reynolds数对单相水条件的相似规律进行了修正,对离心泵在不同流体黏度条件下的扬程进行了预测,预测结果与实验测量值相符合.
人工神经网络具有强大的模式识别和数据拟合能力,基于物理经验模型构建约束,在页岩油田产量预测和油气生产安全评估等方面获得了广泛应用[19].王沐晨等[20]采用径向基函数法进行训练集的数据降维,减少了神经网络待定参数的个数,有效提高了气动力降阶模型的预测精度.Gölcü[21]采用人工神经网络预测了深井泵分流叶片的扬程-流量曲线.网络采用梯度下降、动量梯度下降和Levenberg-Marquardt学习算法,获得了较好的预测结果.Huang等[22]提出了一种混合神经网络来预测离心泵单相条件下的能量性能(扬程、功率和效率),将理论损失模型纳入反向传播神经网络,通过自动确定隐层节点数来优化神经网络结构.当前,基于神经网络预测离心泵水力特性的研究主要集中在单相条件,气液两相条件下多相混输泵增压特性预测仍需要进一步研究.
气液两相间巨大的物性差异和高速旋转的叶轮使得气液相参数在时空分布上具有高度不均匀性,引起混输泵两相增压特性随入口气液流量表现出强烈的非线性特征.当前研究建立的经验关联式和动力学模型适用区间狭窄,仅对于部分结构和特定流动参数范围内的气液增压有较好的预测精度,普适性较差.另外,分区域增压特性的预测方法往往在边界处会产生较大的误差.对于如何将低级数混输泵研究总结的相关规律向现场应用的高级数混输泵进行推广,相关报道仍较为欠缺.
本文研制了工业参数级多相混输实验平台和25级离心式多相混输泵,构建了定转速、低增压级数混输泵气液增压神经网络,结合变转速气液两相的相似规律和高增压级数混输泵内部气液流动参数更新,实现了高增压级数混输泵气液增压性能的预测.通过实验获得的多级离心式混输泵在不同入口气液流量下的气液增压数据,对以上预测方法进行了检验.
1 实验系统与多级混输泵结构
本文构建预测方法所需要的混输泵气液两相增压实验数据,通过动力工程多相流国家重点实验室自主研发的工业参数级深海油气采输管道流动实验平台获得.多相混输泵实验测试系统主要分为4个部分,包括液相管路、气相管路、混输泵测试段和数据采集部分,如图1所示.实验工质为空气和水,系统最高设计压力为30 MPa.工质水经由两台同型号的高压柱塞泵从水箱增压输送,单台柱塞泵最大流量14 m3·h-1.水的流量采用科氏质量流量计测量(RHM30FET2),量程为0~600 kg·min-1,测量精度为0.15%.空气压缩机提供高压气源,经稳压罐稳定压力至10 MPa,经过减压和质量流量计计量与液相混合进入混输泵测试段.低气相流量采用RHM015L型流量计,量程为0~0.6 kg·min-1,精度为0.5%.高气相流量采用RHM06GET2型流量计,量程为0~20 kg·min-1,精度为0.5%.混输泵入口压力通过安装在混输泵出口的气动调节阀进行调节.安装在管线末端的气液分离器能够稳定系统压力并实现气液分离,体积为1 m3.空气经过气液分离器上部管路减压排入大气,水通过底部管路和气动调节阀减压后进入水箱完成循环.多相混输泵实验参数范围如表1所示.

图1 多相混输泵气液增压实验系统Fig.1 The gas-liquid pressurization experimental system for the multiphase pump
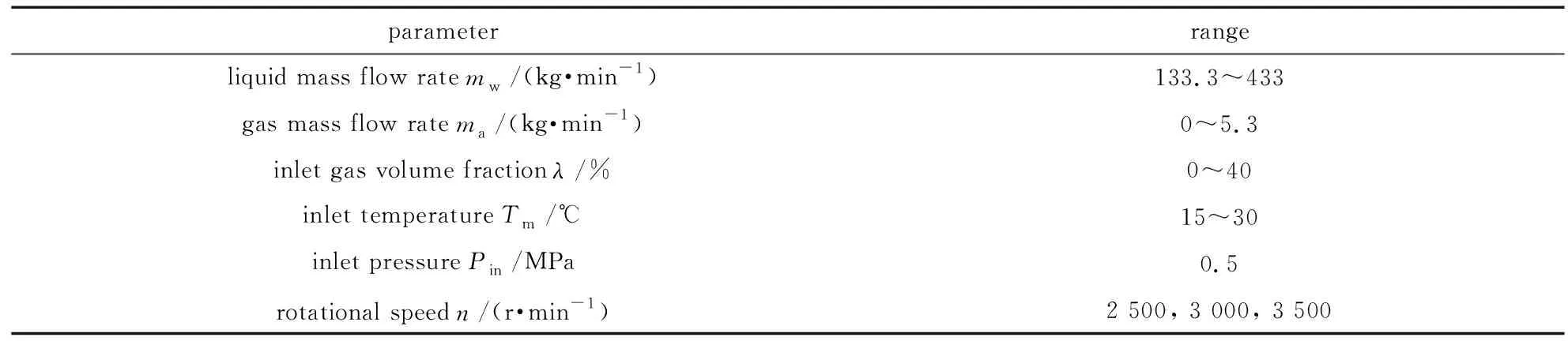
表1 实验参数范围Table 1 Ranges of experimental parameters
本文研究的离心式多相混输泵由25个相同结构的增压级串联组成,如图2所示.每个增压级包含叶轮、扩压器和连接的滑动轴承等部件.单相水条件下泵的最高效率设计点流量为28.5 m3·h-1,单级扬程为23.5 m,设计转速为3 500 r·min-1,比转速为107.叶轮入口直径为65 mm,出口直径为127 mm.叶轮叶片入口角为30.7°,出口角为33.9°,叶片数为7.

图2 多级多相混输泵与压力压差传感器布置Fig.2 The structure of the multistage multiphase pump and the arrangement of differential pressure sensors
为了实现仅采用低级数混输泵的气液增压数据预测高级数混输泵气液增压特性,本文对25级混输泵划分了若干增压单元.逐级测量级间压力和压差信号需要使用大量传感器.笔者之前的工作研究了相同叶型结构的3级混输泵气液增压特性[23].因此,本文采用每隔3级结构布置压力测点的方式,即在第1级、第4级、……、第25级的扩压器中间位置分别布置压力测点,划分了8个增压单元,如1~3级、4~6级、……、22~25级.例如,在第1级和第4级的两个压力测点处布置压差传感器,获得了第1~3级的气液两相增压.混输泵内部沿流动方向的压力不断增加,8个增压单元的入口压力不同,能够同时获得不同入口压力下增压单元的气液增压实验数据,有助于减小实验测试工况.
2 混输泵气液两相增压预测方法
2.1 定转速低级数气液两相增压神经网络
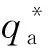
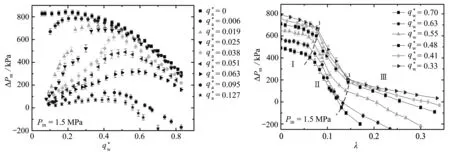
图3 混输泵气液两相增压特性[23]Fig.3 Gas-liquid 2-phase pressurization performances in multiphase pumps[23]注 为了解释图中的颜色,读者可以参考本文的电子网页版本,后同.
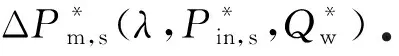
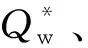
(1)
(2)
(3)
构建的径向基函数神经网络为包含输入层、隐含层和输出层的三层前向网络结构,如图4所示.通过将输入向量空间转换到隐含层空间,将原线性不可分的问题变为线性可分[24].径向基函数的选择满足函数值仅与自变量范数有关,本文选用的径向基函数为Gauss分布函数.当第k个输入向量为Xk=[xk1,xk2,…,xkm]时,网络第j个输出神经元计算结果为
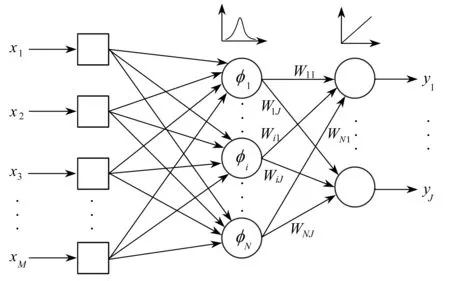
图4 径向基函数神经网络结构Fig.4 The structure of the radial basis function neural network
(4)
采用随机选取样本中心的方法,为保证足够的预测准确度和泛化能力,需要确定合适的隐含层神经元数量和扩散速度.分别改变扩散速度和神经元数量,随机选取三级混输泵测试集(数目为200),计算经过训练的神经网络对应的测试集输出.将上述步骤重复100次并将预测误差取均值,获得当平均相对误差最小时对应的扩散速度与神经元数量.本文采用试算法确定神经元数为400,扩散速度为0.2.
2.2 变转速条件气液增压能力计算
单相水条件下,对于离心式、混流式和轴流式水泵,在满足几何相似、运动相似和动力相似的基础上,实验泵和模型泵的水力性能也具有相似特征,学者们将其总结为水泵相似定律.其中,几何相似是运动相似和动力相似的前提.根据Moody图,高Reynolds数区域处于阻力平方区,在满足几何相似和速度相似的条件下,可认为满足黏性力相似.因此,通常在单相水泵的研究中,主要根据几何与运动相似判断流动状态的相似[25].
与单相水条件不同,由于叶轮旋转产生较大的离心加速度和压力梯度,在叶轮流道内部容易发生气液相分离,进而表现出具有不同界面结构的气液流型.不同气液流型对应不同的动力学状态.学者们通过旋转叶轮可视化实验揭示了叶轮内部气液流型转变诱发的增压恶化机制[9,26-27].Matsushita等[16,28]研究发现,处于相同气液流型条件下离心泵的两相扬程存在相似规律.仿照单相条件,下文将给出不同转速下满足气液两相相似的混输泵两相扬程计算方法.
在多级混输泵内部,由于对气体压缩作用显著,气相的可压缩性不能忽略.通常将气体假设为理想气体.Hm为气相等温压缩条件下混输泵的气液两相扬程,大小等于以气相质量分数为权重的气相扬程和液相扬程之和:
(5)
仿照单相水泵,将混输泵两相流量Qm定义为当地状态下的气相体积流量与液相体积流量之和:
Qm=Qw+Qa.
(6)
由于气体的可压缩性,从多级混输泵入口到出口,沿流动方向气相逐级压缩明显,气相体积显著变小,混输泵进出口的两相流量存在较大差别.图5为不同入口含气率下,混输泵两相流量随增压级数的变化规律.当增压级数较低时,两相流量随级数增大近似线性降低.因此,对于三级混输泵,将两相流量定义为混输泵进出口两相流量的算数平均值Qm=(Qm1+Qm2)/2.根据混输泵进出口气相和液相流量的质量守恒,混输泵进出口两相流量关系如下:

图5 不同入口含气率下,混输泵两相流量随增压级数的变化规律 图6 变转速条件三级混输泵气液两相增压相似的验证Fig.5 Variations of the 2-phase flow rate of the multiphase pump with the stage number under different inlet gas volume fractions Fig.6 Verification of similarity in gas-liquid pressurization under variable rotational speeds in a 3-stage multiphase pump
(7)
对于三级多相混输泵,在变转速条件下含气率分别为5%,10%,20%和30%,通过相似规律将两相扬程折算至设计转速条件的结果,如图6所示.Qm,nd和Hm,nd分别为折算至设计转速条件下的两相流量和两相扬程.不同转速条件下的实验数据点均能较好地遵循同一条曲线分布,符合两相相似规律.因此,可以通过设计转速条件下的混输泵气液增压特性计算其他转速条件下的两相扬程,进而获得两相增压特性:
(8)
(9)
2.3 高增压级数流动参数更新
为获得更高增压级数混输泵的气液两相增压,采用人工神经网络完成三级增压结构的增压预测后,需要进行下一增压单元的入口流动参数更新,以便进行递推计算.本文基于等温压缩假设,对下一级增压单元的入口压力和入口含气率采用如下公式进行更新计算:
Pin,Z+3=Pin,Z+ΔPm,
(10)
其中,Pin,Z+3为下一增压单元的入口压力,Pa;Pin,Z为当前增压单元(三级结构)的入口压力,Pa;ΔPm为当前增压单元的气液两相增压,Pa;Z表示增压级数.
(11)
其中,λ为混输泵入口含气率;Pin为混输泵入口压力,Pa;λZ+3为下一增压单元的入口含气率.
对多级混输泵在变转速条件下,气液两相增压特性预测的基本算法进行总结,如图7所示.首先,输入混输泵入口流动条件(λ,Pin,Qw,n0,Z0),即入口含气率、入口压力、液相流量、转速和目标增压级数.对转速进行判定,并将两相流量折算至设计转速条件.对输入参数进行无量纲归一化处理.将无量纲参数输入到已经完成训练的三级混输泵气液增压神经网络中,获得以三级结构为单元的气液增压特性.随后,进行转速判定,并依据两相相似规律将两相增压折算至原转速条件.下一步进行增压级数判断,若当前增压级数不低于目标级数,则需要对中间级进行插值计算,并对所有增压级求和,最后输出总体气液增压结果.若当前级数低于目标级数,则需要进行下一增压单元气液增压特性计算.基于等温压缩假设计算,并更新下一增压单元的级间入口压力、级间入口含气率与增压级数.将更新结果重新输入神经网络中计算下一单元的气液增压.不断循环向下游计算,直至增压级数不低于目标级数,通过中间级插值,并对所有增压级求和,输出混输泵总体气液增压.
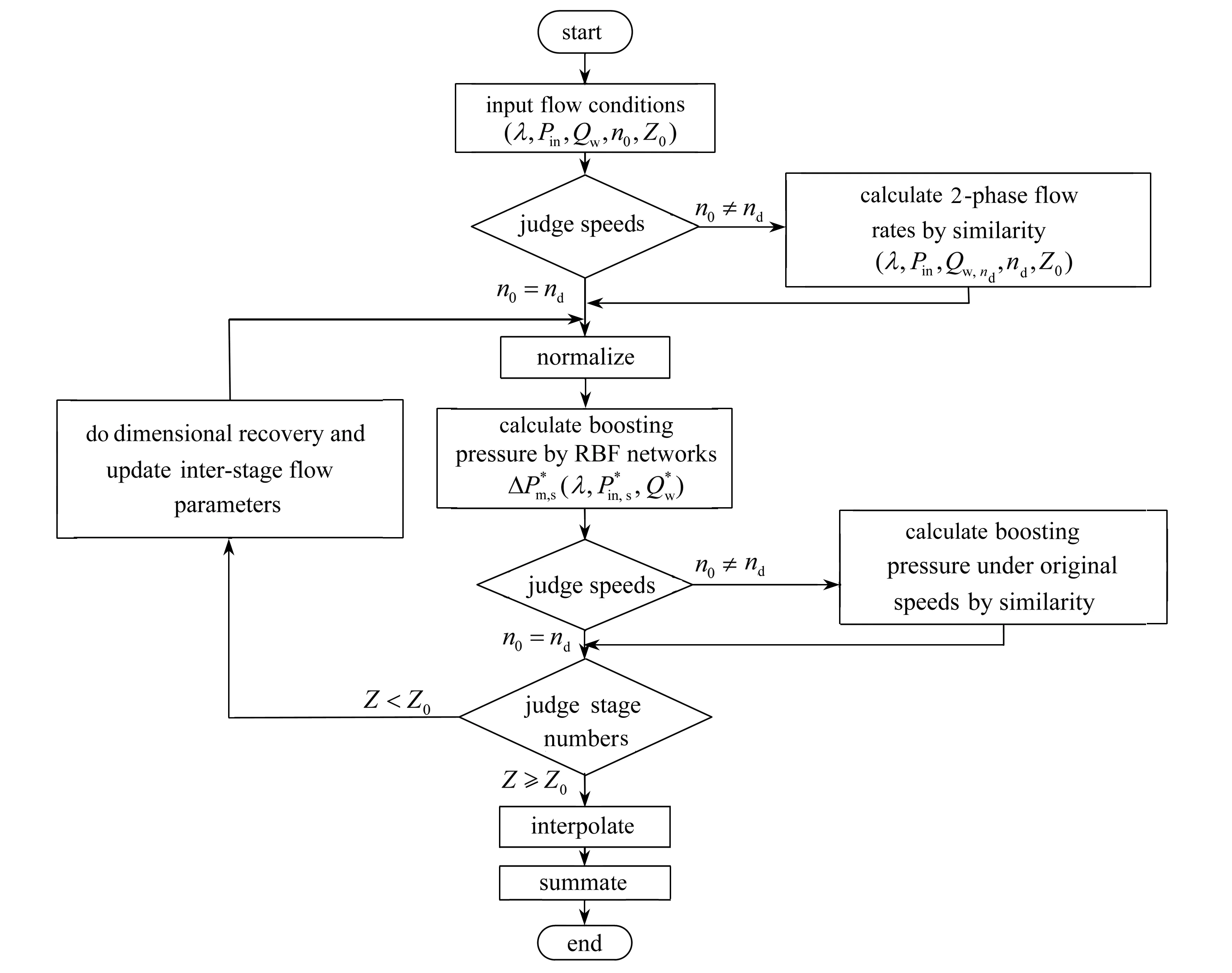
图7 变转速多级混输泵气液增压预测算法流程Fig.7 The flow chart of the gas-liquid pressurization prediction algorithm for multistage multiphase pumps under variable speeds
3 预测结果与讨论
采用本文提出的混输泵气液增压特性预测方法,对不同转速条件下的三级多相混输泵气液增压特性的预测结果进行分析,转速条件分别为2 500 r·min-1,3 000 r·min-1和3 500 r·min-1.为减少构建神经网络过程中对训练样本选择的主观性,随机选取设计转速3 500 r·min-1条件下的实验样本构建神经网络,用于其他转速条件下的增压预测.重复测试100次,获得混输泵入口含气率间隔为0.05,并得到三级混输泵气液两相增压的平均值和对应的标准差,如图8所示.图中实线代表采用样条曲线光顺后获得的不同转速下,混输泵气液增压实验性能曲线.从图中可以看出,不同转速下的三级混输泵气液增压预测值与实验曲线吻合度较好.当发生明显增压恶化,在混输泵气液增压快速下降的位置,由于样本点相对稀疏导致预测误差偏大.

图8 不同转速下,三级混输泵气液增压预测值与实验值比较 图9 不同增压级数混输泵气液两相增压预测值与实验值比较Fig.8 Comparison between the predicted and experimental values of gas-liquid pressurization performance of the 3-stage multiphase pump at different rotational speeds Fig.9 Comparison between the predicted and experimental values of gas-liquid pressurization performance of multiphase pumps with different stages
下面将分析不同增压级数条件下,混输泵气液两相增压预测值与实验值的差别.同样重复测试100次,获得混输泵入口含气率间隔为0.05,不同级数混输泵气液两相增压的平均值和对应标准差,如图9所示.不同级数混输泵气液增压的预测值与实验曲线吻合度较好.随增压级数增大(3~21级),混输泵发生明显增压恶化的含气率逐渐增大.与三级混输泵类似,当气液增压发生明显恶化时,对应的气液两相增压预测误差逐渐增大.另外,预测误差随增压级数增大,表现出误差逐级增大的特点.因此,低增压级数混输泵性能的准确预测是提升高增压级数混输泵预测精度的前提.
最后,综合对不同增压级数和转速条件的混输泵气液增压特性预测结果进行分析.液相流量范围为14~26 m3·h-1,入口含气率为0%~44.0%,转速分别为2 500 r·min-1,3 000 r·min-1和3 500 r·min-1的多级混输泵实验测试样本数量为38,46和57.采用本文提出的预测方法获得的多级混输泵气液增压预测相对误差平均值如表2所示.随增压级数增加,由于计算中对增压单元两相增压的逐级叠加,导致误差放大.采用本文的预测方法对不同增压级数和转速条件混输泵气液增压预测的平均相对误差在15%以内.

表2 不同转速和增压级数混输泵气液增压平均预测相对误差Table 2 The average relative errors for predicting gas-liquid pressurization performances of multiphase pumps with different stages under variable rotational speeds
4 结 论
为实现高增压级数多相混输泵在变转速条件气液增压特性的准确预测,本文搭建了工业参数级多相混输气液增压实验平台,通过级间布置压力压差传感器,实验获得了25级离心式混输泵在不同转速和气液流量下的气液增压特性.提出了适用于高增压级数、变转速条件的混输泵气液增压预测方法.构建了定转速、低增压级数混输泵气液增压人工神经网络.采用相似规律将变转速条件的气液增压转换至设计转速条件.对多级混输泵划分增压单元,考虑气相可压缩性进行流动参数更新,实现了变转速、高级数混输泵气液增压的预测.气液增压预测误差在发生明显增压恶化的位置达到最大,并随级数增大逐级增大.低级数混输泵增压的准确预测是提升高级数混输泵预测精度的前提.对不同增压级数(3~25级)和转速条件(2 500~3 500 r·min-1)混输泵气液增压预测的平均相对误差在15%以内.该方法可以为其他类型混输泵的气液增压预测提供参考,能够指导油气输运现场计算确定混输增压级数,为评估和调控油气生产提供依据.

