基于材料时变参量的挖补修理胶层内剪应力研究

闫登杰 陈淑仙，2 丁镇源

（1 中国民用航空飞行学院航空工程学院，广汉 618307）

（2 中国民用航空飞行学院，四川省通用航空器维修工程技术研究中心，广汉 618307）

文摘 以AS4/3501-6 材料的挖补修理为研究背景，基于材料热、力学参数的时变特性，分别为补片和胶层建立了热-力-化学多物理场耦合的有限元模型，研究了不同挖补角度和胶层厚度对胶层残余剪应力的影响，探索了不同挖补修理设计方案下的修理过程中胶层残余剪应力分布。结果表明：挖补角度、胶层厚度的增大均会加剧胶层残余剪应力集中；减小挖补角度，可有效降低胶层残余剪应力及沿胶层径向平均剪应力梯度；3°挖补角度下胶层径向中点残余剪应力比15°下降低17%，径向平均剪应力梯度降低92%；减小胶层厚度，胶层残余剪应力减小但平均剪应力梯度增大，0.3 mm 胶层厚度下胶层径向中点残余剪应力比1.5 mm 下降低15%，径向平均剪应力梯度升高30%。经验证三维有限元模型及计算方法正确，为改进修理工艺、提高修复质量提供了依据。

0 引言

挖补修理作为民用航空器复合材料构件损伤维修的主要手段，胶黏剂对修复质量有着重要影响。胶黏剂具有良好的间隙填充能力和韧性，固化后形成可以抵抗机械应力、温度和环境侵蚀的牢固粘合，是母板与修补片高性能和灵活连接的关键。但胶黏剂、母板与修补片的热学和机械性能失配会导致胶黏剂区高应力/应变集中。温度变化通过在系统中引起热应力和通过改变黏弹性黏合剂的机械性能来影响黏合剂粘合。具有不同线胀系数（CTE）的材料或具有几何差异的类似材料的局部机械连接会在黏合剂的热固化过程中导致面板显著变形［1-2］。除影响美观，零件的变形还会对接头的完整性造成显著的有害影响，例如面板的局部屈服、增加的残余应力，粘合中引起的拉伸残余应力可能导致结构损坏和脱粘，从而降低粘合耐久性，甚至完全丧失粘合力。

刘国春等［3］研究了双面贴补和挖补两种修理方式的修复效果，结果表明挖补修理方式的修复效果要优于贴补修理。W.FENG等［4］研究了不同厚度（3.5、4.5、6、7 mm）的复合材料层压板的挖补修理效果，实验结果表明不同厚度复合材料层压板的修复效率是稳定的。M.KASHFUDDOJA等［5］建立了不同形状修理模型，讨论了补片形状对修复效果的影响。唐庆如等［6］、王渊涛等［7］研究了挖补角度对梯形台修补片内部热应力的影响。刘哲［8］利用线弹性本构模型计算了不同纤维体积分数、铺层方式等因素对层合板残余应力的影响。Z.H.XIE等［9］研究了挖补角度对复合材料损伤构件剩余强度的影响，结果表明挖补角度越小抗拉强度越大。J.PUENTES等［10］研究了胶黏剂在固化过程中模量的变化，A.G.CASSANO等［11］通过研究10、20、30 mm 厚度胶层固化时的温度，优化了固化后构件的机械性能。H.P.KIRCHNER等［12］、田可可等［13］的研究表明界面处的剪应力是应力传递的主要方式，同时决定胶结性能的主要残余应力为集中在周边的轴向和剪切应力。

胶层残余剪应力大小直接影响修复质量。目前，挖补修理固化过程胶层残余剪应力的研究相对空缺。本文以AS4/3501-6材料的挖补修理为研究背景，基于材料热、力学参数的时变特性，分别为补片和胶层建立了热-力-化学多物理场耦合的有限元模型，研究了不同挖补角度和胶层厚度对胶层残余剪应力的影响，探索了不同挖补修理设计方案下的修理过程中胶层残余剪应力分布，为改进修理工艺、提高修复质量提供了依据。

1 理论模型

1.1 热化学模型

AS/3501-6 为热固性复合材料，热传导控制方程为［14］：

式中，ki（i=x，y，z）为热导率，为生热率，表达式为［14］：

式中，Vf为纤维体积分数，HR为单位质量复合材料固化放热量，α、dα/dt分别为固化度、固化速率。

AS4/3501-6 的固化度和固化速率可由固化动力学方程计算［14］：

式中，Ki、Ei、Ai为反应速率常数、活化能、频率因子，参数值如表1所示［14］。

表1 AS4/3501-6固化动力学参数Tab.1 Curing kinetics parameter of AS4/3501-6

1.2 热学参数控制方程

树脂和纤维热学性质在固化过程中具有时变特性，准确描述树脂及纤维热参量的变化过程是保证计算精度的关键。

AS4 纤维密度ρf在固化过程中保持1 790 kg/m3不变，AS4 纤维比热Cf、沿纤维及垂直于纤维方向的热导率kfL、kfT与温度线性相关［14］：

3501-6环氧树脂的密度ρr与固化度相关［14］：

3501-6 环氧树脂的比热Cr和热导率kr是温度和固化度的线性函数［14］：

AS4/3501-6 复合材料的密度、比热和热导率可由以下混合率方程［14］计算：

式中，B=2（Kr/KfT-1）。

1.3 力学模型

3501-6树脂的力学特性可由CHILE（α）本构模型描述，其模量在固化过程中随α的瞬时变化关系为［8］：

式中，αmod=（α-αgel）/（1-αgel），αgel为树脂凝胶化点的固化度，取值0.57。Er0、Er∞分别为树脂黏流态和玻璃态时的模量。

AS4/3501-6 为横观各向同性材料，其应力应变关系为［8］：

上式可简写为：

式中，σi为残余应力，Q为刚度矩阵，可由细观力学自洽模型［8］计算，εi为应变。

复合材料总应变εij为热应变和化学应变的叠加：

式中，λi（i=1，2，3）为材料三个方向的线胀系数。可由下式计算［15］：

式中，λr、λ1f、λ2f线胀系数、纤维平行于纤维和垂直于纤维方向的线胀系数，νr、ν12纤维泊松比。E1f平行于纤维方向的模量。

式中，Vsh为树脂固化后体积变化率，取值5%。复合材料不同方向的固化收缩应变=1，2，3）可由细观力学混合率公式计算［15］。

AS4纤维及3501-6树脂力学性能参数见表2［8］。

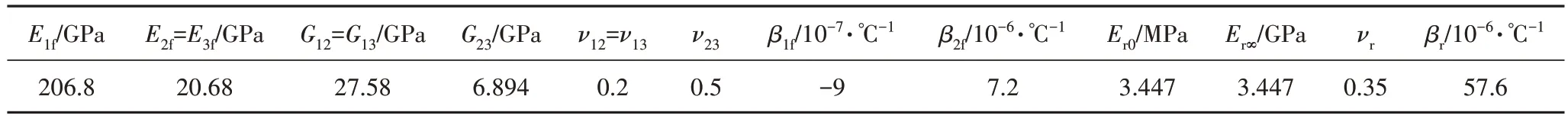
表2 AS4碳纤维及3501-6树脂力学性能参数Tab.2 Mechanical properties of AS4 carbon fiber and 3501-6 resin

2 计算方法与算例验证

基于上述热化学模型及线弹性力学模型，通过对有限元软件的二次开发，建立了热-力-化学多物理场耦合的三维有限元模型，采用Coupled tempdisplacement计算方法预测了复合材料挖补修理过程中胶层残余剪应力的变化历程。为验证计算模型及二次开发程序的准确性，采用参考文献［8］算例进行验证。图1（a）为复合材料平行于纤维方向模量（E1）和垂直于纤维方向模量（E2）与文献值的对比情况，图1（b）为树脂弹性模量（Er）和剪切模量（Gr）与文献值的对比情况，由图1 可知，固化过程中复合材料及树脂力学参数变化过程与文献结果一致，因此本文计算模型和二次开发程序是可靠的。

图1 树脂及复合材料模量计算值与文献值比较 Fig.1 Comparison of calculated modulus of resin and composite materials with literature values

3 物理模型及边界

3.1 物理模型

本文针对圆台型复合材料修理方式进行建模，物理模型尺寸为300 mm × 300 mm × 6 mm，损伤半径为30 mm，母板及补片材料均为AS4/3501-6，铺层角度均为0°，胶层材料为3501-6 树脂。分别设计了不同挖补角度(3°、6°、9°、12°、15 °)及不同胶层厚度(0.3、0.6、0.9、1.2、1.5 mm)的修理方案，讨论了挖补角度及胶层厚度参数变化对胶层残余剪应力变化历程及分布的影响，物理模型如图2所示。

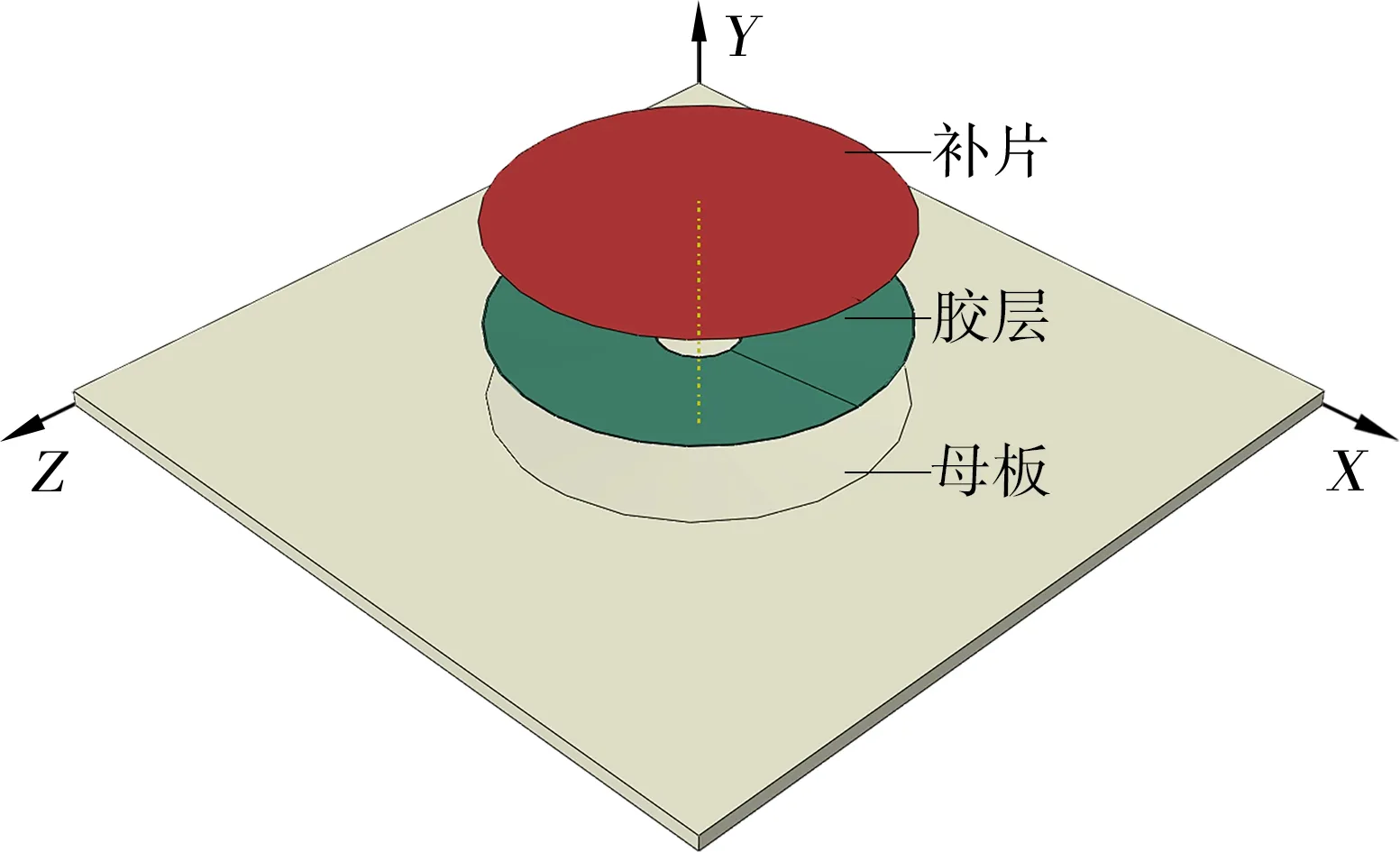
图2 挖补修理物理模型Fig.2 Geometry model of scarf repair

根据所采用的补片形貌特征，分别选取胶层半径中间点（A）作为分析点、胶层半径（l）为分析路径，用于分析修理参数的变化对胶层剪应力状态的影响，如图3所示。

图3 分析点及分析路径Fig.3 Analysis points and analysis paths

3.2 边界条件

设置计算初始条件为：

计算中，设置母板及补片上表面温度与电热毯温度一致，其他面绝热：

式中，TS（t）为母板及补片上表面温度，TH（t）为电热毯温度，由固化工艺温度曲线决定，固化工艺温度曲线如图4所示。

图4 固化工艺温度曲线Fig.4 Curing process temperature profile

同时，计算过程中固定母板及补片上表面：

式中，u（t）为母板及补片上表面位移。

4 结果与讨论

4.1 挖补角度对胶层剪应力的影响

不同挖补角度下分析点A 的固化度和最大残余剪应力（τ）变化历程如图5（a）（b）所示。7 700 s 之前为零应力阶段，胶层、补片和母板受热膨胀，同时胶层和补片还会固化收缩，此时，三者应力应变状态应当复杂，但补片及胶层树脂处于黏流态，传力能力弱，产生的残余剪应力趋于迅速松弛，导致此阶段残余剪应力非常小，可忽略不计。7 700～14 500 s 为胶层残余剪应力变化的第一应力阶段，7 700 s 时，胶层及补片固化度达到凝胶点固化度，树脂剪切模量迅速增大。树脂固化度从0.68 增至1，如图5（a）所示，树脂固化收缩主要发生在此阶段，同时树脂剪切模量从1.277 MPa 增至1.277 GPa［图1（b）］，但树脂较为松弛，残余剪应力增速放缓。随着固化度的提高，树脂逐渐呈现玻璃态性能，应力松弛减弱，残余剪应力持续增大，直至胶层及补片完全固化，但此阶段胶层残余剪应力仍远小于固化结束时残余剪应力。14 500 s后为第二应力阶段，胶层及补片已固化完成，完全呈现玻璃态性能。在该降温阶段，随固化工艺温度下降，受补片、胶层及母板降温收缩失衡效应的影响，胶层残余剪应力持续迅速增大，并在固化周期结束时达到最高。

图5 不同挖补角度下胶层A点固化度及残余剪应力变化历程Fig.5 Curing degree and residual shear stress history at point A of the adhesive for different scarf angles

由于零应力阶段胶层树脂尚处于黏流态，模量小，不同挖补角度（β）下，该阶段A 点残余剪应力均近似于0。胶层A 点残余剪应力于第一应力阶段开始发生差异。3°挖补角度下，母板与补片体积差最小，材料间热膨胀失衡程度最低，同时补片体积最大，固化过程中化学收缩应变可有效抵消部分热应变，导致其残余剪应力最低。14 500 s 时，3°挖补角度下胶层A 点残余剪应力仅为1.51 MPa，比15°挖补角度下A 点残余剪应力小5.47 MPa。第二应力阶段，由于胶层和补片已完成固化，降温过程中再无固化收缩应变，热胀冷缩效应成为胶层A 点残余剪应力继续增大的唯一因素，材料间热膨胀失衡程度成为不同挖补角度下A 点残余剪应力差异的关键。3°挖补角度下材料间热膨胀失衡影响最小，胶层A 点残余剪应力增速最慢，第二应力阶段中不同挖补角度下胶层A 点残余剪应力差值持续增大，直至固化周期结束。固化周期结束时，3°挖补角度下A点残余剪应力为47.06 MPa，比15°挖补角度下A点残余剪应力低9.68 MPa，残余剪应力降低17%。

图6 为固化周期结束时，胶层径向积分路径l的残余剪应力分布情况。圆台型补片形状决定了材料间热膨胀失衡程度为沿路径l两端小中间大，导致路径l上残余剪应力分布呈现中间大两端小的“反浴盆”曲线形式，残余剪应力在l中部均匀分布，过度平缓，但路径两端残余剪应力的迅速降低导致应力梯度主要集中在路径两端。挖补角度越小由热膨胀失衡导致的应变差（Δε）越小，产生的残余剪应力越小，同时，挖补角度的减小还会导致路径l长度增大，残余剪应力过度缓慢，导致路径l平均剪应力梯度越小，3°挖补角度下沿路径l平均剪应力梯度（∇τ）最小，比15°挖补角度下减小了92%。

图6 不同挖补角度下沿路径l的残余剪应力Fig.6 Residual shear stress along path l for different scarf angles

图7 为固化周期结束时不同挖补角度下胶层残余剪应力云图。各向同性树脂在固化过程中受两侧各向异性材料的影响显著，复合材料z向线胀系数大于x向，导致胶层z向应变始终大于x向应变，残余剪应力云图呈现“8”字型向外辐射分布，应力随辐射半径的增大而逐渐减小，残余剪应力过渡较为缓慢。随挖补角度的增大，胶层总体受力情况不变，但由于纤维沿x向分布，胶层及母板x向收缩应变对胶层影响较小，导致最大剪应力区域逐渐扩大并沿z向扩散，向胶层边界靠近，剪应力愈加集中。

图7 不同挖补角度下胶层剪应力云图Fig.7 Shear stress distribution in the adhesive for different scarf angle

4.2 胶层厚度对胶层剪应力的影响

不同胶层厚度（δ）下胶层A点残余剪应力变化历程如图8 所示。A 点残余剪应力变化趋势与图5（b）整体一致，由于不同胶层厚度下挖补角度均为6°，材料间热膨胀失衡主要是由于胶层厚度的变化引起。零应力阶段，A点残余剪应力稳定地保持在一个极小的数值，约为0.03 MPa。第一应力阶段，相同挖补角度下，胶层固化过程中的固化收缩应变为残余应力产生的主要原因，但不同胶层厚度下A 点残余剪应力几乎相同，大小均在2.7～2.9 MPa 间。结合图5（b）可得出结论：第一应力阶段胶层残余剪应力差异主要由挖补角度主导，胶层厚度的影响可以忽略；第二应力阶段，胶层厚度的增大加剧了材料热膨胀失衡程度，在补片与母板同向收缩应变相同的基础上，胶层收缩应变增大，导致固化周期结束时，胶层厚度越小，A 点残余剪应力越小，0.3 mm 胶层厚度下A 点残余剪应力大小为47.36 MPa，比1.5 mm 厚度下A点残余剪应力低15%。

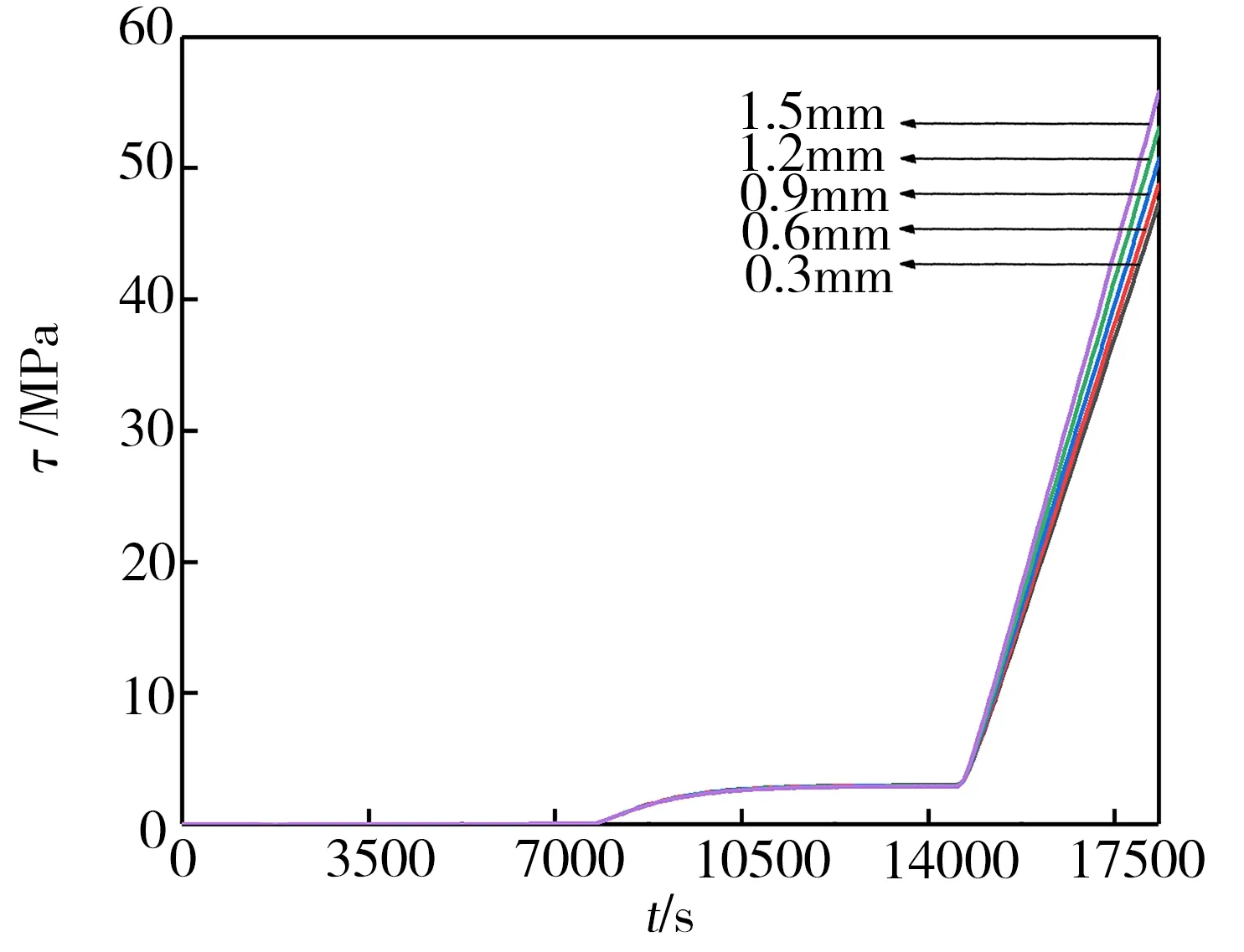
图8 不同胶层厚度下胶层A点残余剪应力变化历程Fig.8 History of residual shear stress at point A of the adhesive for different adhesive thicknesses

图9为不同胶层厚度下路径l的残余剪应力分布情况。不同胶层厚度下路径l残余剪应力分布亦呈现“反浴盆”曲线形式，但残余剪应力沿l变化整体呈现平缓趋势，路径l两端残余剪应力梯度较大。对比图6 可知，挖补角度同样为造成残余剪应力沿l分布不均的主导因素，但胶层厚度对路径l的平均剪应力梯度的影响不可忽略。随胶层厚度的增大，树脂用量的增加，固化过程中载荷传递效率提高［16］，胶层内剪应力梯度有效减小。固化周期结束时，1.5 mm 胶层厚度下路径l平均剪应力梯度为7.86 MPa·m-1，0.3 mm 胶层厚度下平均剪应力梯度比1.5 mm 下提高30%。胶层厚度增大，剪应力增大，但平均剪应力梯度减小。

图9 不同胶层厚度下沿积分路径l的残余剪应力Fig.9 Residual shear stress along path l for different adhesive thicknesses

图10为不同胶层厚度下胶层残余剪应力分布云图。胶层残余剪应力以x、z轴为对称轴对称分布，呈现“8”字形，并以小半径圆孔附近的最大应力区域为中心向外辐射。同时，最大应力区域在z向的辐射范围大于x向的辐射范围，呈现明显的各向异性。随胶层厚度的增大，界面最大残余剪应力增大，但衰减迅速［16］，最大应力区域逐渐缩小并向胶层小半径圆孔边界移动。固化周期结束时，1.5 mm胶层厚度下，胶层残余剪应力最大，应力集中最明显。胶层厚度的增大，其各向同性的性质削弱了复合材料各向异性性质对胶层残余剪应力分布的影响，最大应力区域在z向和x向的辐射范围差减小，但加剧了胶层小半径圆孔边界的剪应力集中。

图10 不同胶层厚度下胶层剪应力分布Fig.10 Shear stress distribution in the adhesive for different adhesive thicknesses

5 结论

（1）基于材料热力学参数时变特性，建立了多材料系统的热-力-化学耦合的三维有限元模型，数值模拟了挖补修理过程中胶层剪应力场，并与文献结果进行对比验证，证明了理论模型及计算方法的正确性。

（2）减小挖补角度，可有效降低胶层残余剪应力及残余剪应力沿胶层径向的平均剪应力梯度，3°挖补角度下胶层径向中点（A）残余剪应力比15°下降低17%，沿l平均剪应力梯度降低92%。

（3）降低胶层厚度，胶层残余剪应力减小但平均剪应力梯度增大，0.3 mm胶层厚度下，胶层径向中点（A）残余剪应力比1.5 mm 下降低15%，沿l平均剪应力梯度升高30%。