基于用户大数据的工况分类与构建方法

柳子强 王晓旭 王大志

（中国第一汽车股份有限公司研发总院，长春 130013）

1 前言

目前，可靠性试验中采用的城市汽车行驶工况通常为欧洲城市循环工况，该工况加减速过程简单，与实际车辆行驶状态差距较大，已不能满足车辆开发测试的需要[1]。

使用用户大数据可以更准确地描述用户实际驾驶状态，有效提高试验工况与用户驾驶行为的关联性。本文通过大数据的提取和处理，并结合主成分分析、K 均值聚类、马尔可夫排序等数据处理方法，实现对用户各种驾驶行为下典型工况的构建，以进一步提高试验结果与用户实际驾驶状态的一致性。

2 数据处理

2.1 数据信息

本文采用的大数据主要来自某企业某车型用户大数据平台，基于用户实际驾驶车辆定期反馈的数据进行研究，用户的选取主要参照以下原则：选取该车型用户车辆总行驶里程由高到低排序的前10 个城市，下载相应用户某自然年全年的行驶数据作为分析对象。前10 个城市所有用户的总行驶里程如表1所示。

表1 某车型用户总行驶里程由高到低排序的前10个城市

2.2 数据整理

进行数据提取和聚合后，需要对大数据片段进行划分，从而形成多个完整的行驶工况。选取具有代表性的行驶工况，将这些工况的速度-时间数据按一定的时间周期划分，可得到多个运行片段[2]，片段划分遵循如下原则：

a.将连续2 个速度为0 的时间段划分为一个运行片段，某个片段的速度-时间曲线如图1所示。

图1 某单一片段速度-时间曲线

b.计算划分后的运行片段的最大速度，若最大速度不超过5 km/h，则将此片段视为无效片段，并从片段集合中去除。

c.对剩余的有效运行片段进行编号。

本文最终将获得的数据划分为104 357 个运行片段。

2.3 特征参数的选取和计算

从对驾驶特点的描述角度，本文选取了18个特征参数，如表2所示。

表2 工况特征参数

对每一个驾驶循环工况进行18 维特征参数计算，最终形成带有特征参数信息的片段集合，称为特征参数矩阵。

3 基于主成分分析法的数据分析

本文采用主成分分析法将高维且具有一定相关性的复杂特征指标转化为低维的多个互不相关的主成分，并保留原始特征参数中的大量信息[3]，为后续的分类和分析工作提供基础。

3.1 主成分分析过程

假设共有n个运行片段，每个运行片段有p个特征参数，将计算出的所有运行片段的特征参数矩阵记为X。设随机变量Xi的均值为μi、协方差矩阵为Σi，则通过主成分分析，对p个特征参数进行线性变换，生成的综合指标即为主成分，记为y1、y2、……yp。其中特征参数矩阵X可以表示为：

式中，xij(i=1,2,…,n,j=1,2,…,p)为特征参数矩阵中的特征参数。

经过变换后主成分的表达式为：

式中，x1~xp为原始特征参数；lij(i,j=1,2,…,p)为主成分变换后的参数矩阵；l1′~lp′为各主成分中特征参数的载荷系数。

根据相关系数矩阵或协方差矩阵求解各主成分yp，其中方差及协方差计算公式分别为：

式中，lj为协方差参数矩阵。

各特征参数的量纲不同，会引起各变量的分散程度差异较大。在通过协方差矩阵求解特征值与对应的特征向量前，为消除量纲不同带来的不合理影响，常对各原始变量进行标准化处理。标准化处理后的变量为：

式中，E(xj)为X向量的平均值。

向量Z=(z1,z2,…,zp)T的协方差矩阵为相关系数矩阵ρ=[ρ(xi,xj)]p×p。主成分分析后主成分的协方差矩阵为对角矩阵Λ，其对角线元素为相关系数矩阵ρ的特征根λ1、λ2、……、λp。其中相关系数矩阵

各主成分的总累积贡献量可以用r′表示：

根据式（6），第j个主成分的贡献率为λj/r′，则前m个主成分的累积方差贡献率为，当累积贡献率达到80%~90%时，提取前m个主成分，可以代替原始变量中大部分特征信息量。

当特征参数变量x1~xp在某个主成分上的载荷系数近似时，对其主成分的解释较为困难，可以通过因子分析中方差最大化正交旋转法来实现对因子载荷矩阵的旋转，使每个变量在主成分上方差最大化，载荷矩阵每行或每列的元素平方向0 和1 两级分化，因子载荷越接近1 说明相关性越强[4]，以此实现对因子载荷系数的解释。

假设共有n个特征参数，主成分因子数量为m，若每次进行2 个因子的旋转计算，共有m(m-1)/2 种旋转方法，将此视为一次循环，直到因子载荷矩阵中各列的方差和最大且收敛。假设载荷矩阵为A：

令正交矩阵为Q：

式中，φ为矩阵正交后的旋转角度。旋转后的因子载荷矩阵B为：

为使旋转后的因子载荷矩阵各列方差总和V=V1+V2最大，Vj的计算公式为：

以上计算过程均可通过SPSS软件进行，最终得到主成分分析的成分矩阵，将成分矩阵与原始的特征参数矩阵相乘，即可得到主成分分析结果。

3.2 主成分分析结果

通过主成分分析，可以得到降维后的结果，其总方差解释如表3所示。

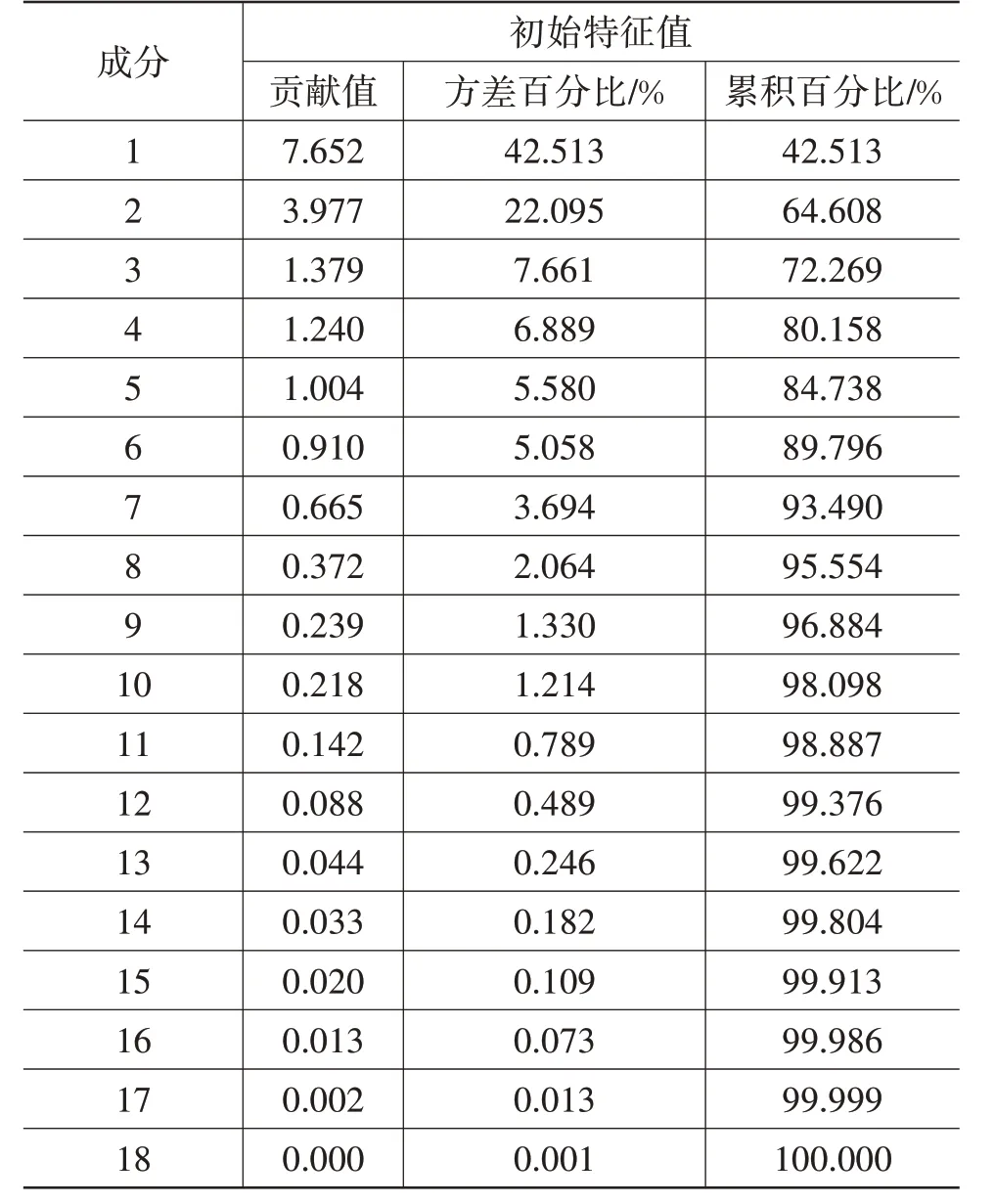
表3 总方差解释

其中方差百分比即为此主成分所包含的原始信息的比例，累积百分比80%以上的成分即可覆盖大部分的原始信息。本文中，前4 个主成分累积贡献量为80.158%，因此可将原始数据的特征参数矩阵由18维降低到4维。

4 基于K均值聚类方法的分类过程

作为经典的数据挖掘方法，K 均值聚类方法是一种无监督的学习方法[5]。在不明确运行片段分为哪些典型工况时，运行K 均值聚类算法给定聚类数量K，即为K类典型工况。按照点与点之间的距离，将每个点分到距离最近的类簇中心所代表的类别中，所有样本点分配完成后重新计算该类簇中所有样本点的平均值，即为新的聚类中心点，之后继续迭代分类，直至类簇中心点的变化很小或达到给定的迭代次数[6]。

4.1 K均值聚类分析过程

K 均值聚类需要事先指定K值，因此需要一种可以确定最优K值的方法，目前主要有4 种方法，即方差比准则、大卫-博丁指数、轮廓系数法、手肘法。

在实际分析中，分类数量不应出现较大值，因此可在小范围内采用穷举法，然后根据判定式进行最优解的确认，本文对分类数在2~10范围内进行穷举，综合考虑4种方法的计算结果，确定K=4。

4.2 K均值聚类结果

本文使用SPSS 软件对主成分分析后形成的4维特征参数矩阵进行聚类，取K=4，最大循环次数为100次，部分结果如表4所示。

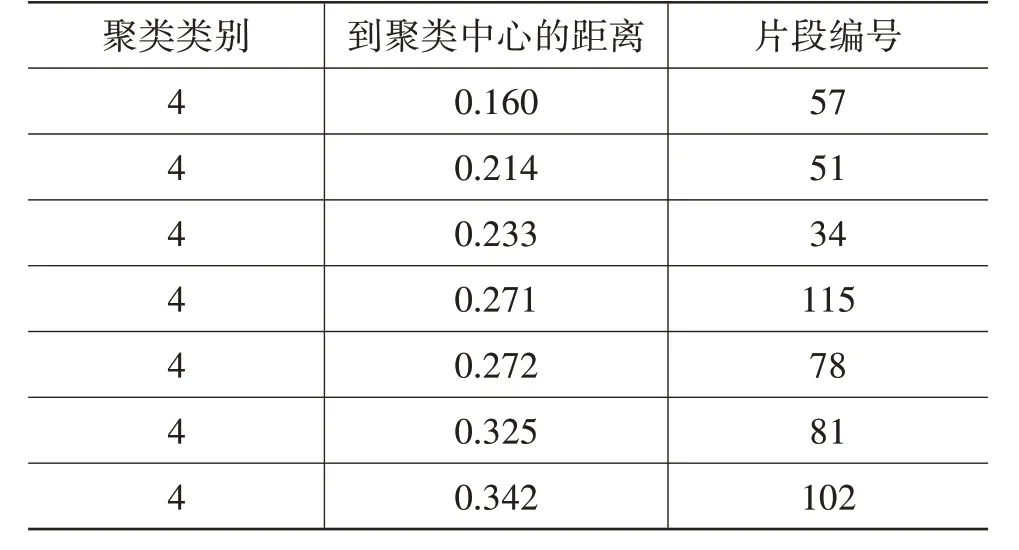
表4 K均值聚类部分结果

在结果中，每个运行片段都有一个对应的聚类编号，以及该片段到聚类中心的距离，与聚类中心距离越近，代表这一片段越能反映其所在分类的特征。因此，选取4 类中与聚类中心最近的4 个片段，即为这4类各自的代表片段，结果如表5所示。

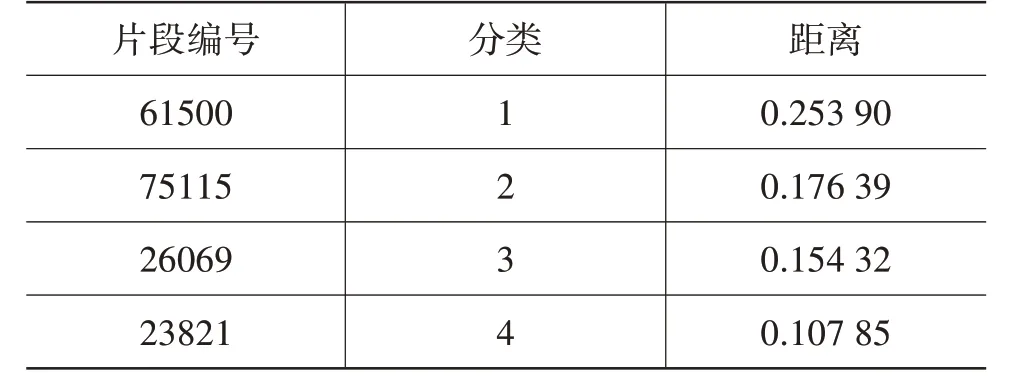
表5 代表片段编号和距离

由于代表片段为与聚类中心距离最近的片段，因此在定义分类的含义时，可以直接观察代表片段的特征对分类进行解释。综合考虑各类代表片段的信息后，对各分类的特征解释如下：

a. 分类1。城郊工况，主要典型特征为车速处于中高速，有较为频繁的加减速，加速度较大，其典型片段如图2所示。

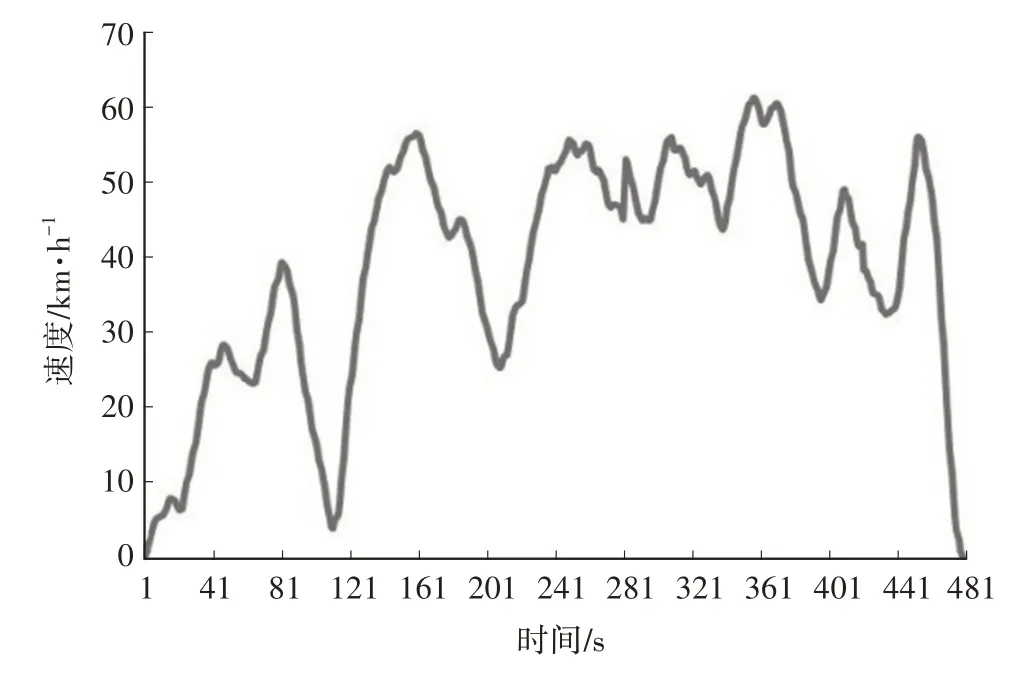
图2 城郊工况速度曲线

b. 分类2。高速工况，主要典型特征为车速长时处于高速段，减速不剧烈，加速度也较小，其典型片段如图3所示。

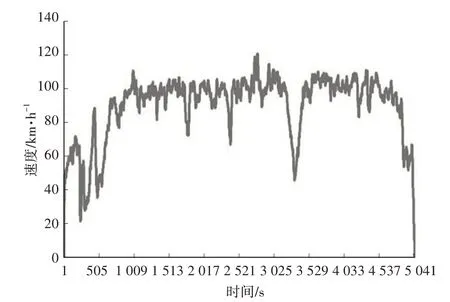
图3 高速工况速度曲线

c. 分类3。城市拥堵工况，主要典型特征为车速处于低速段，加速度较小，其典型片段如图4 所示。

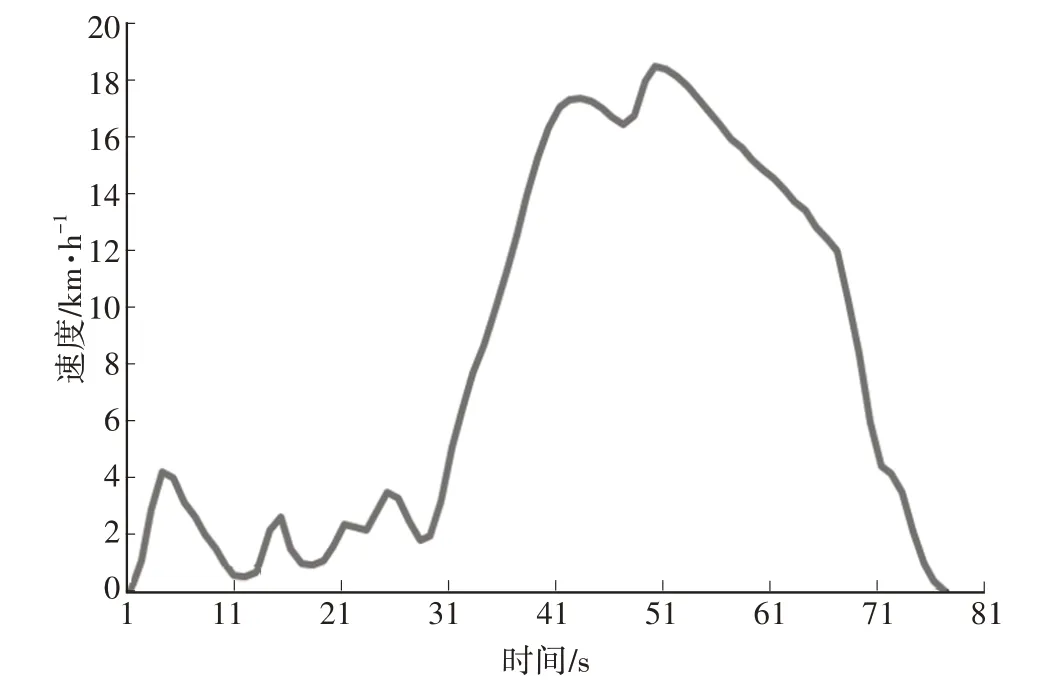
图4 城市拥堵工况速度曲线

d. 分类4。城市快速路，主要典型特征为速度处于中速，有一定加减速，加速度较大，其典型片段如图5所示。

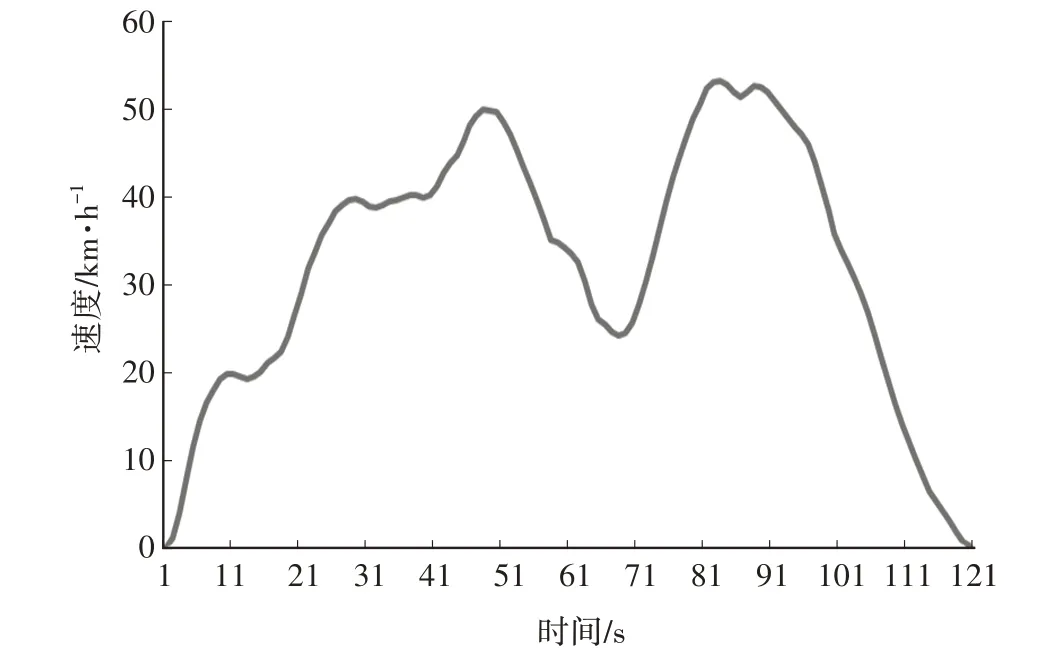
图5 城市快速路工况速度曲线

5 基于马尔可夫链的片段排序过程

5.1 试验片段的选取

选取各分类中用户行驶过程损伤较大的片段作为试验工况，以便缩短试验工况的时间，利用20 位用户行驶大数据全过程的平均总损伤与试验工况的损伤进行协同计算，最终得出各片段循环次数如表6 所示，为了便于计算，循环次数进行取整。

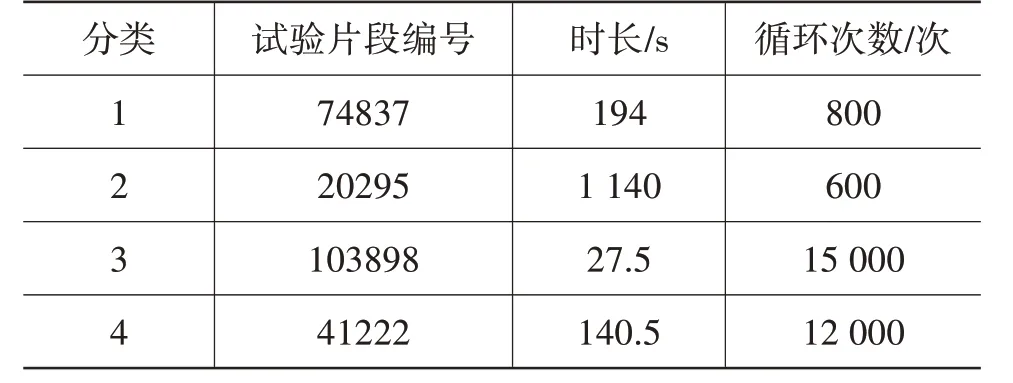
表6 各试验片段及循环次数

试验片段的转速和转矩变化情况如图6所示。

图6 试验片段转速变化情况

5.2 马尔可夫过程

准确复现用户实际使用条件下的载荷作用效果是电驱动系统可靠性评价的核心，其本质是通过合理的工况组合顺序使得各部件性能同步退化到全生命周期设定目标。本文根据马尔可夫原理分析原始工况片段之间的顺序关系。

马尔可夫链实际上是一组离散随机变量的集合[7]，具体指对概率空间(Ω,F,P)内以一维可数集为指数集的随机变量集合X={Xn:n>0}，假设随机变量的取值范围均在可数集内，X=si,si∈s，且随机变量的条件概率满足如下关系：

将式（1）中的X称为马尔可夫链，对于一个固定的马尔可夫链模型，式（11）表明，随着马尔可夫链的增长，链中事件参数的分布不变。基于马尔可夫链的这种性质，通过模型时间转移矩阵构建循环工况能够代表整个原始数据中用户实际行驶工况[8]。

采用最大似然估计法计算各类典型工况间的状态转移矩阵，马尔可夫过程可以通过贝叶斯公式求得稳态概率：

式中，P(Z0)为Z0事件的先验概率；P(Zτ|Zτ-1)为在Zτ-1事件发生的前提下，Zτ事件发生的概率。重复上述过程，N次重复观察的公式为：

通过极大似然函数，假设从工况r转移到工况s，可得出各工况间的状态转移概率方程：

式中，Prs为当前状态工况r转移到下个时刻状态工况s的概率，r,s=1,2,3,4；Nrs为工况r转移到工况s的频次[9]。

将聚类后的4种典型工况特征作为马尔可夫过程的4个状态，构成状态空间，根据每个片段所属的工况类别构建马尔可夫链模型。对于一个固定的马尔可夫过程，通过各工况间的状态转移概率方程，即可计算各工况状态转移概率矩阵[10]。

本文使用nCode 进行辅助计算，马尔可夫转移概率矩阵实际计算结果如表7所示。根据表7，最终的工况顺序为工况3-工况4-工况2-工况1。

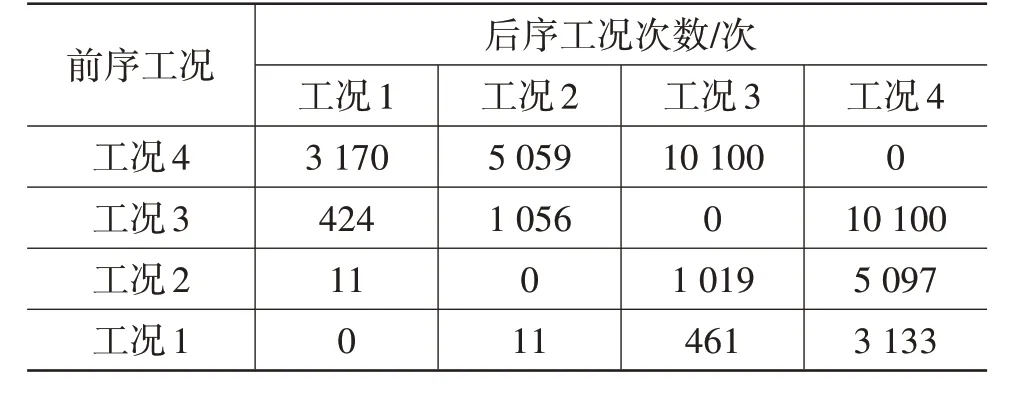
表7 马尔可夫转移概率矩阵

6 工况结果整理

根据以上计算结果，本文构建的工况为：试验工况3 运行150 次，试验工况4 运行100 次，试验工况2 运行6 次，试验工况1 运行8 次；以上工况循环100次。

按运行顺序，各工况示意如图7~图10所示。

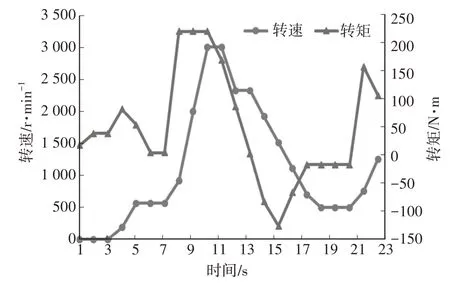
图7 工况3

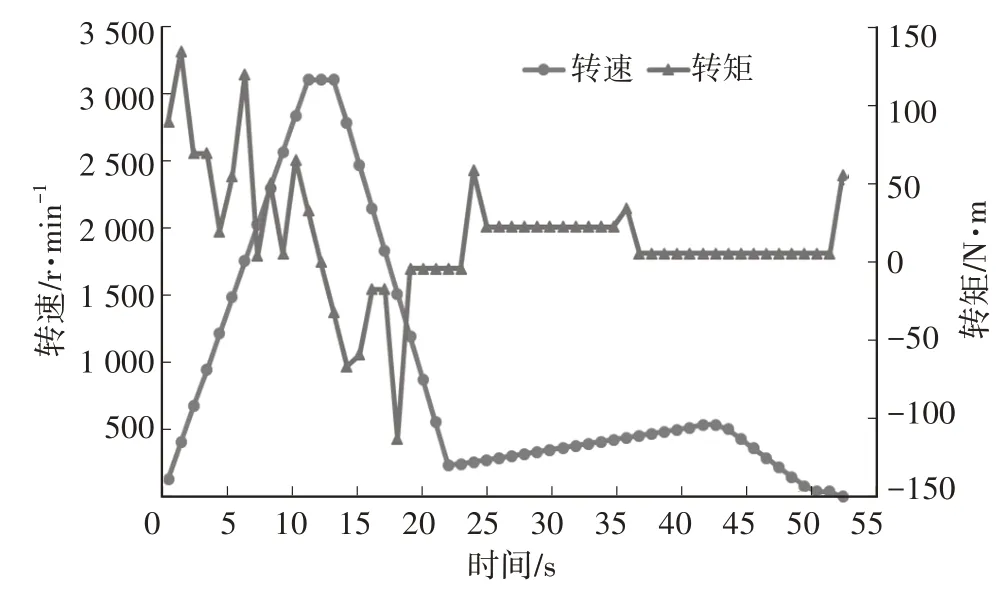
图8 工况4

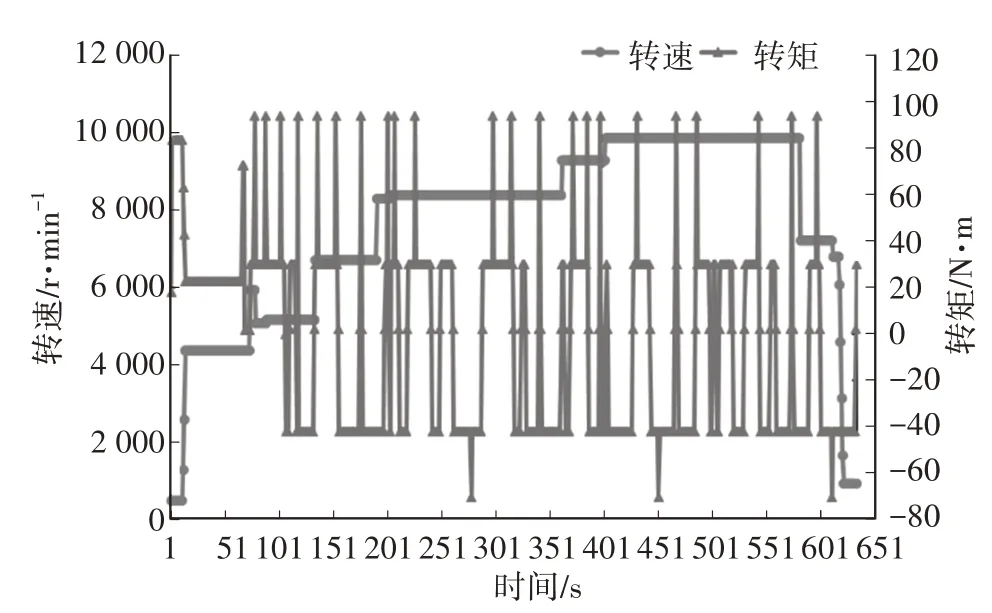
图9 工况2

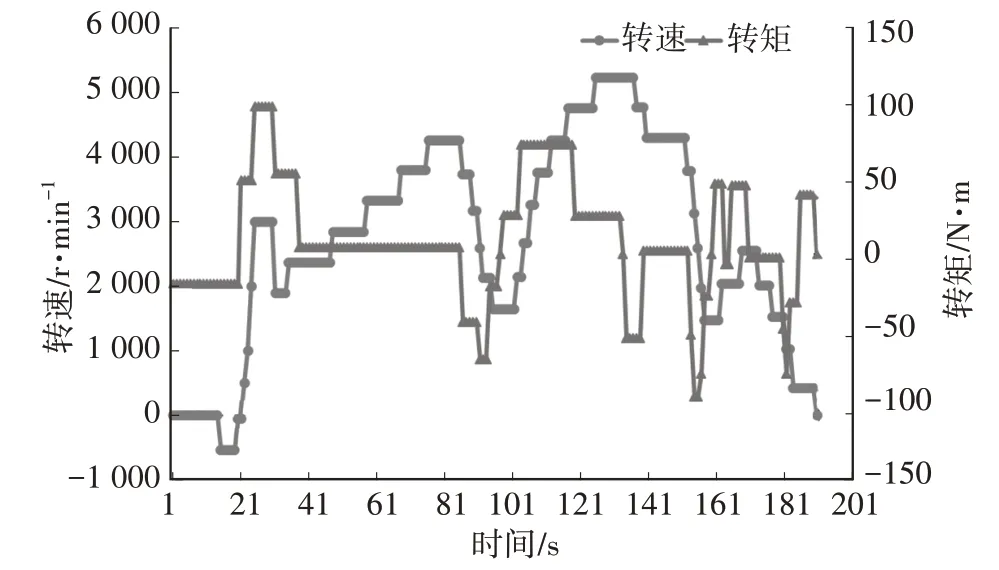
图10 工况1

目前，电驱系统普遍使用的循环耐久试验工况包括定转速定转矩运行，不同转速、转矩下的持续工况循环运行，以及交变工况的循环运行。采用本文提出的方法构建的工况与当前普遍采用的工况相比，具有以下优点：

a.工况由用户数据提取和处理获得，且各工况有对应的含义，能更准确地反映用户实际驾驶时的工况信息。

b. 由于采用了各工况中大数据计算得到的损伤值偏大的用户数据作为代表片段，通过本文方法计算出的工况实际用时将少于目前工况用时，有利于试验周期的压缩。

7 结束语

本文通过对提取后的用户大数据进行主成分分析、K 均值聚类、马尔可夫排序，构建了基于用户大数据的可靠性试验工况，与当前采用的试验参考工况相比，更贴合用户实际驾驶状态。