对一道椭圆联考题的解法与延伸探究
湖南省长沙市南雅中学 (410027) 朱 彬
湖南省长沙市雨花区雅境中学 (410014) 胡晓静
1 试题呈现

(1)求椭圆C的标准方程;
(2)过点F(1,0)作两条斜率都存在且不为0的互相垂直的直线l1、l2,直线l1、l2与椭圆相交于四点为A1、A2、B1、B2,求四边形A1A2B1B2的面积S的最小值.
2 解法探究

下面重点探究第(2)小题的解法.
思路1:处理直线与椭圆线(圆锥曲线)的交点问题,可设交点坐标为(x1,y1),(x2,y2),同时联立直线与椭圆(圆锥曲线)的方程,得x1+x2(或y1+y2),x1x2(或y1y2),再把相关弦长用x1,x2(或y1,y2)表示出来,并将x1+x2(或y1+y2)及x1x2(或y1y2)整体代入,进而解得问题.这就是“设而不求”的方法.该解题过程充分体现将几何问题转化为代数问题,即通过代数运算研究几何图形性质,图形问题代数化的解析几何的本质.

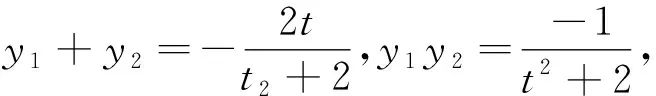

点评:解法1取直线斜率的“倒数”t为参数,设出直线的“横斜截式”方程并与椭圆方程联立,运用“设而不求”和均值不等式解答.“设而不求”是一种重要的解题手段,常能避开因盲目演算而导致无益的循环运算,达到简捷、准确的解题效果.另外,解法1中还用到了对角线互相垂直的四边形面积的一个结论:“对角线互相垂直的四边形的面积等于它的两条对角线长的乘积的一半”.
思路2:解答涉及到焦点的椭圆(圆锥曲线)问题时,灵活运用椭圆(圆锥曲线)定义,既可以深化对椭圆(圆锥曲线)这一数学概念的理解,也能提高学生运用定义去分析和解决问题的能力,开拓思维视野.

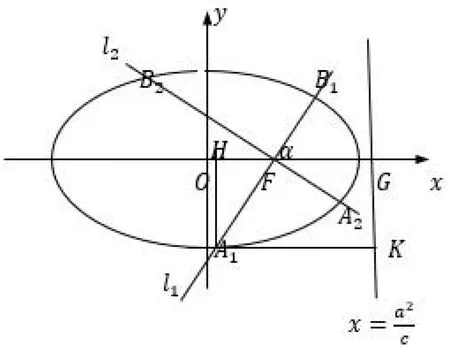
图1

点评:解法2取直线的倾斜角为参数,在运用椭圆的第二定义的基础上,利用几何图形转化为角的弦函数关系,进而利用三角函数同角平方关系、三角恒等变换及弦函数的有界性求解,充分体现了“回归定义”的重要性.
3 延伸探究
3.1 试题延伸
问题1 我们能否将试题第(2)小题的结论延伸到椭圆的一般情形?答案是肯定的.

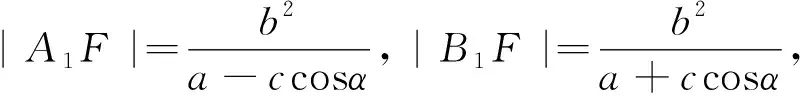
3.2 类比延伸
问题2 我们知道,圆锥曲线之间有许多相互类似的性质或结论,能否将椭圆的一般结论(即结论1)分别类比到双曲线和抛物线,得到类似的结论?答案同样是肯定的!

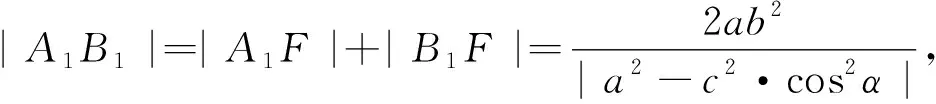

结论3 过抛物线C:y2=2px(p>0)的焦点F作两条斜率都存在且不为0的互相垂直的直线l1、l2,直线l1、l2与抛物线相交于四点为A1、A2、B1、B2,则四边形A1A2B1B2的面积S有最小值为8p2.

结语:我们平时的解题过程中,要适时地将问题推广延伸为一般性的结论用于解决相关问题.久而久之,就能逐步培养学生灵活多变的思维品质,培养其探索精神和创新意识,从而真正把对能力的培养落到实处,提高其数学核心素养.

