高观点视角下对一道高三联考试题的溯源探究

福建省南平市高级中学 (353000) 江智如 蔡 珺

1 试题呈现

题目定义Tn(cosθ)=cosnθ,(n∈N*)．

(1)证明:Tn(cosθ)=2Tn-1(cosθ)cosθ-Tn-2(cosθ);

(2)解方程:8x5+10x3-x2-12x-2=0(x∈C)．

2 试题分析

本试题是雅礼十六校2023届高三上学期第一次联考第17题,是一道结构紧凑,背景丰富,综合性强的试题．考查三角函数恒等变换、函数与方程、利用导数判断函数零点等相关知识,考查化归与转化思想、推理论证能力和运算求解能力,试题具有区分与选拔功能．

2 解法探究

(1)由余弦函数两角和差公式可得cosnθ=cos[(n-1)θ+θ]=cos(n-1)θcosθ-sin(n-1)θsinθ,cos(n-2)θ=cos[(n-1)θ-θ]=cos(n-1)θcosθ+sin(n-1)θsinθ,两式联立得,cosnθ=2cos(n-1)θcosθ-cos(n-2)θ,即Tn(cosθ)=2Tn-1(cosθ)cosθ-Tn-2(cosθ)．

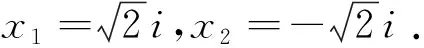
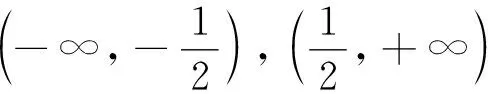
在上述解析中,第(1)问考查三角恒等变化,考生根据已有的三角函数知识可以顺利证明;而第(2)问的解析令人产生疑惑:①第一步的因式是如何分解出来?②方程的解为什么会是余弦值?著名数学大师F·克莱因(Klein)指出:“基础数学的教师应该站在更高的视角(高等数学)来审视、理解初等数学问题,只有观点高了,事物才会显得明了简单”[1]．为此,笔者追本溯源,从高观点视角对本试题溯源探究．

3 背景溯源

溯源1 行列式的基本性质[2]:①行列式的某一行(列)中公因式可以提出去;②把行列式的某一行(列)的倍数加到另一行(列)上,行列式的值不变．

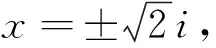
溯源3 第一类切比雪夫多项式:T0(x)=1,T1(x)=x,Tn+1(x)=2xTn(x)-Tn-1(x),(n∈N*)．它是以俄国著名数学家切比雪夫(Tschebyscheff)名字命名的重要特殊函数,源起于多倍角余弦函数和正弦函数的展开式,是与棣美弗定理有关、以递归方式定义的多项式序列,是计算数学中的一类特殊函数[4]．

由于一元三次方程的求根公式比较复杂,所以在中学阶段没有介绍一般的求根公式,只涉及特殊形式的一元三次方程．《普通高中数学课程标准(2017年版2020年修订)》(以下简称《课标(2020年修订)》)要求:“对于多项式,能利用导数求不超过三次的一元多项式函数的单调区间,借助函数的图象,运用二分法求解方程的近似解”[5]．因此,本试题通过构造函数f(x)=8x3-6x-1,确定方程的根均在区间(-1,1)中．然后由第(1)问的结论推导出cos3θ=4cos3θ-3cosθ,而方程8x3-6x-1=0中三次项与一次项的系数比恰好为4∶3,于是根据切比雪夫多项式,令方程的根为cosα,再通过余弦函数的恒等变换最终求出方程的解,这就是第(2)问解析中方程的最终解为余弦值形式的缘由．

4 高考链接

在历年高考试卷中也出现切比雪夫多项式的身影,多以三角函数为载体,用以考查学生推理论证能力和运算求解能力．

题目1 (2010年高考江苏卷第23题)已知△ABC的三边长都是有理数．(1)求证:cosA是有理数;(2)求证:对任意正整数n,cosnA是有理数．

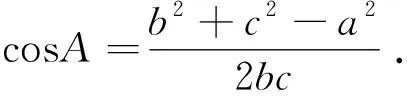
(2)当n=1时,cosA是有理数;当n=2时,cos2A=2cos2A-1也是有理数．

假设n≤k(k≥2,k∈N*)时,结论成立,则coskA,cos(k-1)A均是有理数,那么当n=k+1时,cos(k+1)A=2cosAcoskA-cos(k-1)A,由于cosA,coskA,cos(k-1)A均是有理数,故cos(k+1)A也是有理数,所以,当n=k+1时,结论成立．

综上所述,对任意正整数n,cosnA是有理数．

评析:本试题第(1)小问考查余弦定理和有理数性质的相关知识,大部分考生可以利用余弦函数的恒等变换证明．第(2)小问运用数学归纳法进行证明,其中递推公式:cos(k+1)A=2cosAcoskA-cos(k-1)A就是切比雪夫多项式,考生运用两角和与差的余弦公式进行推导,并不会增加试题的难度,符合课程标准的考查内容和要求,考查考生推理论证能力和运算求解能力,促进逻辑推理素养与数学运算素养提升．

例2 (2010年高考福建卷文科第16题)观察下列等式:

①cos2α=2cos2α-1;

②cos4α=8cos4α-8cos2α+1;

③cos6α=32cos6α-48cos4α+18cos2α-1;

④cos8α=128cos8α-256cos6α+160cos4α-32cos2α+1;

⑤cos10α=mcos10α-1280cos8α+1120cos6α+ncos4α+pcos2α-1.

可以推测,m-n+p=____________．

解法1:根据等式的规律:最高次项的系数为22k-1,故m=210-1=29=512;每个等式的二次项系数满足(-1)n-1·(2k)·k,故p=(-1)5-1·(2·5)·5=50．又等式对任意的α均成立,故在等式⑤中令α=0,有1=m-1280+1120+n+p-1,解得n=-400,所以m-n+p=962．

解法2：由切比雪夫多项式构造函数Tn(cosα)=cosnα,(n∈N),那么有T0(cosα)=1,T1(cosα)=cosα,Tn+1(cosα)=2Tn(cosα)·cosα-Tn-1(cosα),(n∈N*)．于是T10(cosα)=2T9(cosα)·cosα-T8(cosα)=2cos9α·cosα-cos8α=2cos(8α+α)·cosα-cos8α=2cosα(cos8αcosα-sin8αsinα)-cos8α=2cos2αcos8α-cos8α-sin2αsin8α=2cos2αcos8α-cos8α-4sin22αcos2αcos4α=2cos2αcos8α-cos8α+4(4cos4α-4cos2α)(2cos2α-1)(8cos4α-8cos2α+1)=512cos10α-1280cos8α+1120cos6α-400cos4α+50cos2α-1.故m=512,n=-400,p=50,所以m-n+p=962．

评析：本试题以多倍角余弦函数的展开式为载体,考查考生推理论证能力．方法1引导考生观察展开式中各项系数的规律,归纳猜想等式⑤展开式的各项系数,考查特殊与一般思想,符合考生的认知水平．方法2运用切比雪夫多项式直接推导出等式⑤的展开式,计算量比较大,要求考生有扎实的数学运算能力,激发数学学习潜能,体现《课标(2020年修订)》的理念与要求,对日常教学有引导作用．

7 结语

近年来,运用高等数学知识、方法、思想等“高观点”,去分析、研究高考数学问题的解题策略和方法,逐渐成为高考数学研究的趋势和风向标,并取得大量的研究成果．“高观点”是课程改革中的一种创新,对解决初等数学问题有独特作用．高中数学课程具有基础性、选择性和发展性,为不同学生可持续发展和终身学习创造条件[5],培养学生具备进入高等学校进行专业学习和终身发展所需要的必备知识、关键能力和学科素养[6]．因此在日常的教学实践中,教师可以结合高中数学知识要点学习、研究、思考,搜集相关高观点文献资料,精选教学案例,改进教学方式,吸引学生的学习兴趣,拓宽学生思维视野,设计“精致练习”[7],启发学生思考,领会变式、迁移等技巧,激发数学学习潜能,促进学生数学学科素养的提升．