一类绝对值双重最值问题的追根溯源*

浙江省宁波市北仑区明港高级中学 (315800) 贺 旭

一、题引

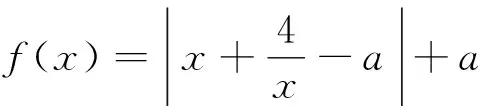
(2)(2018年浙江竞赛12)设a∈R,x∈[0,1],且对任意实数b均有max|x2+ax+b|≥1,求a的取值范围.

上述三个题都是绝对值函数问题.含绝对值的最值问题一直是高考考查的热点和难点,这类问题常常灵活多变、扑朔迷离,那么它是否高不可攀、令人望而生畏呢?当我们将这三个问题放在一起寻找它们的共性时,可以抽象得到它的基本形式是|f(x)-ax-b|,找到统一形式后,就方便我们深入研究.

二、追根溯源

例1 函数f(x)=|x-1|,x∈[-1,1]的最大值为________.

图1

变式1 函数f(x)=|x-b|,x∈[-1,1],其中b∈R.记f(x)的最大值为g(b),当b变化时,g(b)的最小值为________.

图2

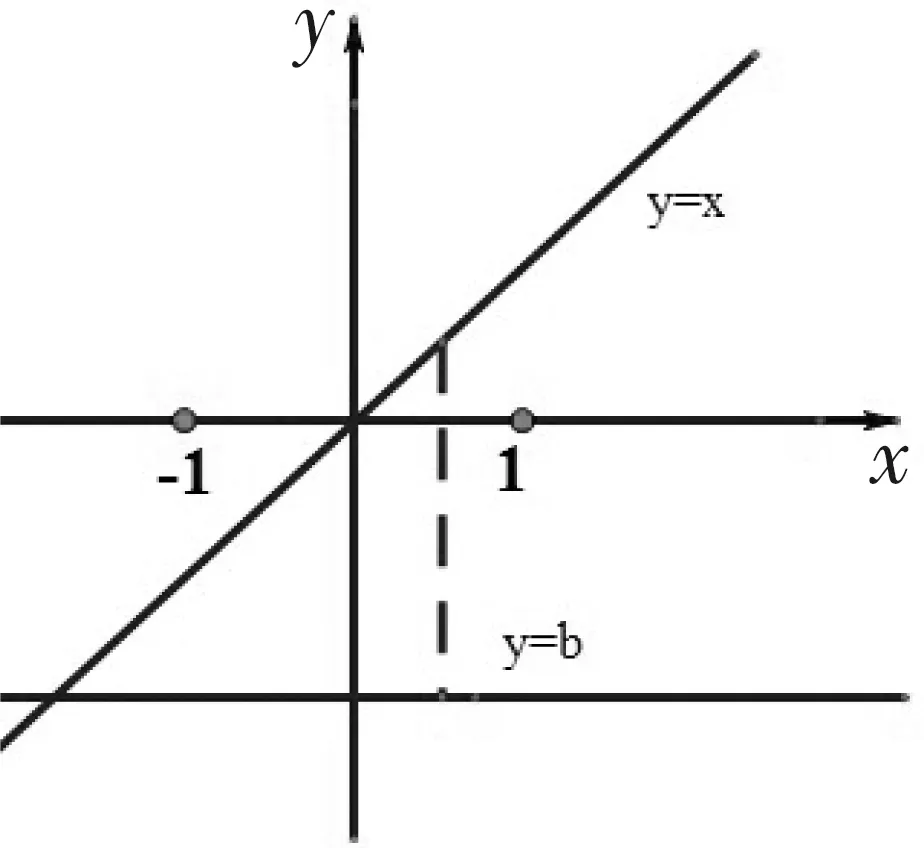
图3

变式2 已知函数f(x)=|x2-b|,x∈[-1,1],其中b∈R.记f(x)的最大值为g(b),则g(b)的最小值为________.

图4

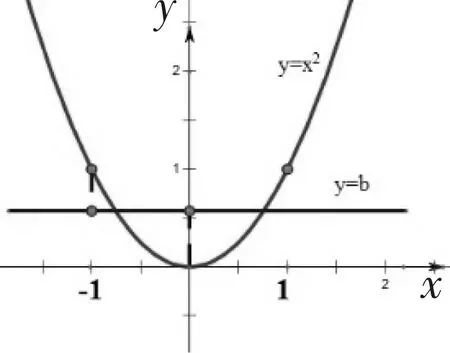
图5

变式3 设函数f(x)=|x2-ax-b|,x∈[-1,1],其中a,b∈R.记f(x)的最大值为M(a,b),则M(a,b)的最小值为________.

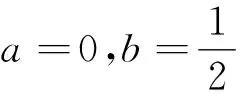
变式4 设函数f(x)=|x2-ax-b|,x∈[0,1],其中a,b∈R.记f(x)的最大值为M(a,b),则M(a,b)的最小值为________.

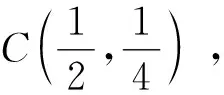
图6

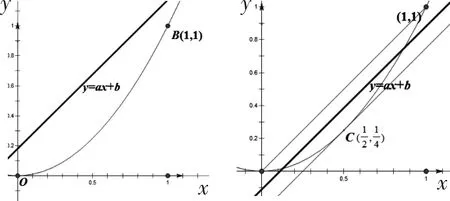
图7 图8

对于以上4个变式,我们采用了统一的方法,利用绝对值的几何意义,将最值问题转化为图形的距离问题.那么对于这类最大值的最小值问题,它是否能推广到更一般的情形,这类问题背后的理论支撑又是什么呢?

三、理论基础

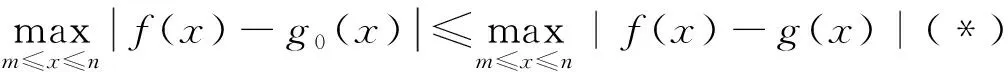
绝对值双重最值的实质是求最大值的最小值,将绝对值里的代数式看成两个函数的差,数形结合,转化为两个函数的纵向距离,通过移动其中一条直线,寻找纵向距离的最值.

本文提供的三个题引中,参数有一个也有二个,有正向提问,也有反向提问,但本质都不变,考查的是minmax|f(x)-g(x)|.主要目的是培养数学抽象能力,及理性思维能力.

本文从“绝对值”的几何意义出发,设计了环环相扣的问题链,从不含参的绝对值问题到含有一个参数的绝对值问题,再到含两个参数的绝对值问题,从对称曲线到不对称曲线,最后提升到切比雪夫最佳逼近直线理论.整个过程自然、生动、明晰,挖掘问题的各个方面,一个完整的理论分析.