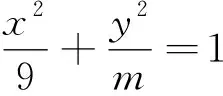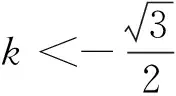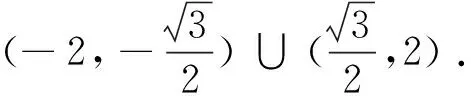例探圆锥曲线问题中的易错点

福建省长汀县第一中学 (366300) 孙微微

圆锥曲线是高考中重点考查的内容,主要重点考查圆锥曲线的几何性质,直线与圆锥曲线的位置关系.本文就针对圆锥曲线中的几类易错点进行举例分析.

易错点1:忽视圆锥曲线标准方程要焦点位置的讨论

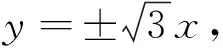
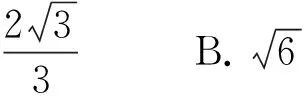
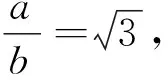
易错警示：双曲线方程因焦点位置不同导致对应的渐近线方程也不一样,因此要讨论焦点的位置.

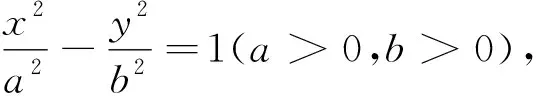
易错点2:忽视椭圆中a、b、c的大小关系

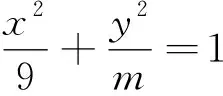
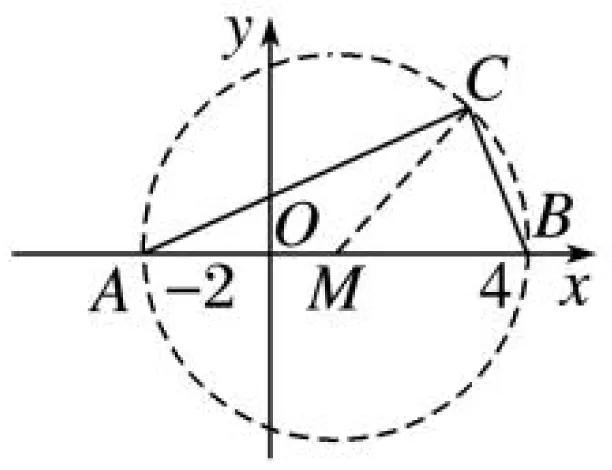
A．m≥4 B．0

C．4≤m<9 D．m≥4且m≠9

易错点3:忽视检验结论

例3 已知Rt△ABC的斜边为AB,点A(-2,0),B(4,0),则点C满足的方程为________．

解析：设C(x,y),由于直角三角形斜边上的中点为M(1,0),如图1所示,则半径为3,即得圆的方程为(x-1)2+y2=9.但是顶点C不能在直线AB上,因此y≠0.因此C点满足的方程为(x-1)2+y2=9(y≠0)．

图1

易错警示：忽视检验结论致错.点C是直角三角形的顶点,即C点不能在直线AB上,所以y≠0．

知识点拨：画图,通过数形结合找到解题方法及限制条件.

易错点4:忽视隐含条件.

例4 已知2x2+y2=6x,则x2+y2的取值范围为________．

解析：由已知得y2=6x-2x2,因y2=6x-2x2≥0,故0≤x≤3,故x2+y2=-x2+6x=-(x-3)2+9.当x=0时,x2+y2有最小值为0;当x=3时,x2+y2有最大值9,故x2+y2的取值范围是[0,9].

易错警示:题中条件包含两个意思:一是y2=6x-2x2,即y2可以用x的代数式表示,二是y2=6x-2x2≥0,即0≤x≤3,这个条件往往被忽略,产生错解.

知识点拨：利用函数与方程的思想是解决本题的突破口.

易错点5:忽视Δ>0这一前提条件

易错警示：在解决直线与圆锥曲线相交且有交点时,需考虑一元二次方程根的判别式大于0,否则容易出错.

知识点拨：运用“一元二次方程根的判别式”是判断直线与圆锥曲线是否有交点的重要方法.