广义风车图的相关矩阵及指标

王雪婷,王 燕

(烟台大学数学与信息科学学院,山东 烟台 264005)

文献[1]定义了距离拉普拉斯矩阵DL(G)=Tr(G)-D(G)和距离无符号拉普拉斯矩阵DS(G)=Tr(G)+D(G)。RANDIC在文献[2]中引入了一个新的距离矩阵,WANG[3]等重新定义并命名为离心率矩阵ε(G)。ε(G)是由D(G)中保留每一行每一列的最大值,其余元素都为零所构成的矩阵,其元素定义为

文献[4]中定义的风车图W(η,s)是由η个完全图Ks组成,且这η个Ks的顶点都连接到同一个节点。KOOIJ等[5]将风车图推广到广义风车图,有三种基本的推广方式。第一种记作W′(η,s),有η个中心节点,η个完全图Ks通过这η个中心节点相连,每个Ks的顶点都连接到同一个中心节点,且只与这个中心节点相连,而η个中心节点构成一个完全图。第二种记作W″(η,s,l),有l个中心节点,这l个中心节点构成一个完全图,η个完全图Ks的顶点都与这l个顶点相连。第三种记作W″′(η,s,l),有l个中心节点,这l个中心节点构成独立集,η个完全图Ks的顶点都与这l个顶点相连。

本文将计算广义风车图的距离矩阵、离心率矩阵的谱半径以及相关指标,下面是本文用到的定义:

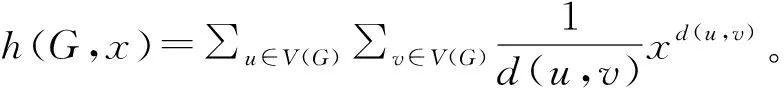
定义6[17]连通图G的乘法Wiener指标定义为π(G)=∏u,v∈V(G)d(u,v)。

本文中,SpecDL(G),SpecDS(G),Specε(G)分别表示DL(G),DS(G)和ε(G)的谱。

1 W′(η,s)的相关矩阵及指标

定理1

其中,α1,α2是方程(α-η+1)(α-3sη+2s+1)-(1-2η)(s-2sη)=0的根;α3,α4是方程α2+(2s+2)α+s+1=0的根。

证明令Pi表示第i行元素全为1,其余元素都为2的η×s阶矩阵,In×n,Jn×n分别表示n-级单位矩阵和n-级全1矩阵,根据距离矩阵的定义易得D(W′(η,s))如下:

其中行标列标均为有序列{u1,u2,u3,…,uη,v11,v12,…,v1s,v21,v22,…,v2s,…,vη1,vη2,…,vηs}。

现对行列式|αI-D(W′(η,s))|作一些初等变换:

(1)从第η+sη-1行开始,依次将第i行乘-1加到第i+1行,其中1≤i≤sη+η,但i∉{1,…,η,η+s,η+2s,η+3s,…,η+ηs};

(2)从第η+sη列开始,依次将第j列加到第j-1列,其中1≤j≤η+sη,但j∉{1,…,η,η+s,η+2s,η+3s,…,η+(η-1)s}。

再将行列式依次按η+ks+2,η+ks+3,…,η+(k+1)s,0≤k≤(η-1)展开,则有|αI-D(W′(η,s))|=(α+1)(s-1)η|A|。其中,

现将第i行乘-1加到第i+1行,i∉{η,2η},再将第j列直接加到第j-1列,j∉{η,2η},则可得

现先按照第一列展开,在展开后得到的两行列式中均再按照第η列展开,如此可得

|A|=[(α-η+1)(α-3sη+2s+1)-(1-2η)(s-2sη)]|B|,

其中,

综上可得

|αI-D(W′(η,s))|=(α+1)(s-1)η[(α-η+1)(α-3sη+2s+1)-

(1-2η)(s-2sη)][(α+2s+1)(α+1)-s]η-1。

定理1得证。

根据定理1中的距离矩阵,可以写出

则DL(W′(η,s))=Tr(W′(η,s))-D(W′(η,s)),DS(W′(η,s))=Tr(W′(η,s))+D(W′(η,s))。

由定理1得定理2和定理3如下:

定理2

其中,β1,β2是方程(β-2sη+s)(β-2η+1)-s(2η-1)2=0的根,β3,β4是方程(β-3sη-2η+1)(β-2sη-η+s)-s=0的根。

定理3

SpecDS(W′(η,s))={3sη-2s+2η-3((s-1)η),γ1,γ2,γ3(η-1),γ4(η-1)},

其中,γ1,γ2是方程(γ-2sη-2η+s+2)(γ-6sη+4s-2η+3)-s(1-2η)2=0的根,γ3,γ4是方程(γ-3sη+4s-2η+3)(γ-2sη-η+s+2)-s=0的根。

定理4

证明令Mi表示第i行元素是0其余元素全为2的η×s阶矩阵,所以根据离心率矩阵的定义,易得

将|δI-ε(W′(η,s))|作如定理1的初等变换,则

定理得证。

定理5在广义风车图W′(η,s)中

π(W′(η,s))=4sη(η-1)3s2η(η-1)。

在W′(η,s)中,d(ui,vpq)=2,1≤i≠p≤η,1≤q≤s,则H(W′(η,s),x)的二次项系数是W′(η,s)中2长路的条数,即等于sη(η-1)。

根据以上证明过程,可以得到

π(W′(η,s))=4sη(η-1)3s2η(η-1)。

在定理5中,当λ=1时,可以得到推论1。

WW(W′(η,s))=η(η-1)+sη(6sη+6η-5s-5)。

定理6 在广义风车图W′(η,s)中

Sc(W′(η,s),x)=s2η+η(η+s-1)+[sη(s2+s+2η-2)+η(η2-2η+1)]x+

sη(η+2s-1)(η-1)x2+s3η(η-1)x3,

Sc(W′(η,s))=η(η-1)(3s3+4s2+2sη+η-s-1)+sη(s2+s+η-1),

综上,

Sc(W′(η,s),x)=s2η+η(η+s-1)+[sη(s2+s+2η-2)+η(η2-2η+1)]x+

sη(η+2s-1)(η-1)x2+s3η(η-1)x3。

根据以上证明过程,可以得出以下结论:

Sc(W′(η,s))=η(η-1)(3s3+4s2+2sη+η-s-1)+sη(s2+s+η-1),

2 W″(η,s,l)的相关矩阵及指标

定理7

SpecD(W″(η,s,l))={-1(l-1+(s-1)η),-s-1(η-1),ζ1,ζ2},

其中,ζ1,ζ2是方程ζ2+(s-l-2sη+2)ζ+(1-l)(s+1)+sη(l-2)=0的根。

证明根据距离矩阵的定义可得

其中行标列标均为有序列{u1,u2,u3,…,uη,v11,v12,…,v1s,v21,v22,…,v2s,…,vη1,vη2,…,vηs}。

现对行列式|ζI-D(W″(η,s,l))|作初等变换:

(1)从l+sη-1行开始,依次将第i行乘-1加到第i+1行,i∉{l,l+s,l+2s,…,l+(η-1)s};

(2)从l+sη列开始,依次将第i列加到第i-1列,i∉{l+1,l+s+1,l+2s+1,…,l+(η-1)s+1}。

再将由这两步得到的行列式依次按2,3,…,l,l+ks+2,l+ks+3,…,l+ks,0≤k≤η-1行展开,则可得到|ζI-D(W″(η,s,l))|=(ζ+1)l-1+(s-1)η|B|,其中,

(ζ+s+1)η-1[ζ2+(s-l-2sη+2)ζ+(1-l)(s+1)+sη(l-2)]。

即

|ζI-D(W″(η,s,l))|=(ζ+1)l-1+(s-1)η(ζ+s+1)η-1[ζ2+(s-l-2sη+2)ζ+(1-l)(s+1)+sη(l-2)]。

定理得证。

根据定理7中的距离矩阵,可以写出

则

DL(W″(η,s,l))=Tr(W″(η,s,l))-D(W″(η,s,l)),DS(W″(η,s,l))=Tr(W″(η,s,l))+D(W″(η,s,l)),

经过如定理7的计算过程,容易得到定理8和9如下:

定理8SpecDL(W″(η,s,l))={0,l+sη,l+s(2η-1)((s-1)η),l+2sη(η-1),l+sη(l-1)}。

定理9SpecDS(W″(η,s,l))={l+sη-2(l-1),l+s(2η-1)-2((s-1)η),l+2s(η-1)-2(η-1),μ1,μ2},其中,μ1,μ2是方程μ2-(5sη+3l-2s-4)μ+(sη+2l-2)(l+2sη-2s-2)+sη(3l+2sη-4)=0的根。

定理10Specε(W″(η,s,l))={-1(l-1),0((s-1)η),-2s(η-1),ξ1,ξ2},其中,ξ1,ξ2是方程ξ2+(2s-2sη-l+1)ξ-2s(l-1)+sη(l-2)=0的根。

证明因为e(ui)=1,1≤i≤l,e(vmn)=2,1≤m≤η,1≤n≤s,所以根据离心率矩阵的定义可以写出

对|ξI-ε(W″(η,s,l))|作如定理7的初等行列变换,经计算可得

|ξI-ε(W″(η,s,l))|=ξ(s-1)η(ξ+1)l-1(ξ+2s)η-1[ξ2+(2s-2sη-l+1)ξ-2s(l-1)+sη(l-2)]。

定理得证。

定理11 在广义风车图W″(η,s,l)中

由以上分析,可以得到:

在定理11中,当λ=1时,可以得到推论2。

WW(W′(η,s,l))=sη(3sη+2l-2s-1)+l(l-1)。

定理12 广义风车图W″(η,s,l)中

Sc(W″(η,s,l),x)=sη(s+l-1)+l(l+sη-1)+[sη(s-1)(s+l-1)+l(l-1)(sη+l-1)]x+

[slη(sη+s+2l-2)]x+s2η(η-1)(s+l-1)x2,

Sc(W″(η,s,l))=sη(s-1)(s+l-1)+l(l-1)(sη+l-1)+

slη(sη+2l+s-2)+2s2η(η-1)(s+l-1),

s2η(η-1)(s+l-1)2。

证明根据定理11的证明过程,当顶点a,b间的距离为0时,即a=b,a在W″(η,s,l)中的度有以下两种情况:(1)度为s-1+l,此时有sη个顶点;(2)度为sη+l-1,此时有l个顶点.故Sc(W″(η,s,l),x)的常数项为sη(s+l-1)+l(l+sη-1)。

当顶点a,b间的距离为2时,它们在W″(η,s,l)中的度均为s,所以Sc(W″(η,s,l),x)的二次项系数为s2η(η-1)(s+l-1)。

综上,

Sc(W″(η,s,l),x)=sη(s+l-1)+l(l+sη-1)+[sη(s-1)(s+l-1)+l(l-1)(sη+l-1)]x。

根据上述分析过程,可得:

Sc(W″(η,s,l))=sη(s-1)(s+l-1)+l(l-1)(sη+l-1)+

slη(sη+2l+s-2)+2s2η(η-1)(s+l-1),

s2η(η-1)(s+l-1)2。

3 W‴(η,s,l)的相关矩阵及指标

定理13SpecD(W‴(η,s,l))={-2(l-1),-1((s-1)η),-(s+1)(η-1),ρ1,ρ2},其中,ρ1,ρ2是方程ρ2+(s-2l-2sη+3)ρ+sη(3l-4)-2(l-1)(s+1)=0的根。

证明易得

经过计算易得

|ρI-D(W‴(η,s,l)|=

(ρ+2)l-1(ρ+1)(s-1)η(ρ+s+1)(η-1)[ρ2+(s-2sη-2l+3)ρ+sη(3l-4)-2(l-1)(s+1)]。

定理得证。

现根据D(W‴(η,s,l))可以写出对应的

则

DL(W‴(η,s,l))=Tr(W‴(η,s,l))-D(W‴(η,s,l)),

DS(W‴(η,s,l))=Tr(W‴(η,s,l))+D(W‴(η,s,l))。

由定理13的计算,得到定理14和定理15如下:

定理14SpecDL(W‴(η,s,l))={0,l+sη,2l+sη(l-1),2sη+l(η-1),2sη+l-s((s-1)η)}。

定理15SpecDS(W‴(η,s,l))={sη+2l-4(l-1),2sη+l-s-2((s-1)η),2sη-2s+l-2(η-1),σ1,σ2},其中,σ1,σ2是方程σ2-(5sη+5l-2s-6)σ+(4l+sη-4)(2sη+l-2s-2)+sη(7l+2sη-8)=0的根。

定理16Specε(W‴(η,s,l))={-2(l-1),0((s-1)η),-2s(η-1),2s(η-1),2(l-1)}。

证明显然e(ui)=2,1≤i≤l,e(vmn)=2,1≤m≤η,1≤n≤s,所以根据离心率矩阵的定义,有

对|τI-ε(W‴(η,s,l))|进行如定理13的初等行和初等列变换,再经过计算可得

|τI-ε(W‴(η,s,l))|=(τ+2)l-1τ(s-1)η(τ+2s)η-1[τ-2s(η-1)][τ-(2l-1)]。

定理17 广义风车图W‴(η,s,l)中

h(W‴(η,s,l),x)=[ηs(s-1)+2slη]x+[s2η(η-1)+sηl(l-1)]x2,

WWλ(W‴(η,s,l))=sη(s-1)+2slη+(2λ-1+22λ-1)[s2η(η-1)+sηl(l-1)],

π(W‴(η,s,l))=2s2η(η-1)+sηl(l-1)。

同理可得:

h(W‴(η,s,l),x)=[ηs(s-1)+2slη]x+[s2η(η-1)+sηl(l-1)]x2,

WWλ(W‴(η,s,l))=sη(s-1)+2slη+(2λ-1+22λ-1)[s2η(η-1)+sηl(l-1)],

π(W‴(η,s,l))=2s2η(η-1)+sηl(l-1)。

在定理17中,令λ=1,可以得到推论3。

定理18 广义风车图W‴(η,s,l),

Sc(W‴(η,s,l),x)=sη(s+l-1)+slη+[sη(s-1)(s+l-1)+slη(sη+s+l-1)]x+

[s2η(η-1)(s+l-1)+s2η2l(l-1)]x2,

Sc(W‴(η,s,l))=sη(s-1)(s+l-1)+slη(sη+s+l-1)+2s2η(η-1)(s+l-1)+2slη(l-1),

证明根据定理17的证明过程,当顶点a,b间的距离为0时,即a=b,则a要么是Ks中的顶点,要么是l个节点,故Sc(W‴(η,s,l),x)的常数项为sη(s+l-1)+slη。

所以

Sc(W‴(η,s,l),x)=sη(s+l-1)+slη+[sη(s-1)(s+l-1)+slη(sη+s+l-1)]x+

[s2η(η-1)(s+l-1)+s2η2l(l-1)]x2。

根据以上证明过程,可得:

Sc(W‴(η,s,l))=sη(s-1)(s+l-1)+slη(sη+s+l-1)+2s2η(η-1)(s+l-1)+2slη(l-1),