利用相位特征筛选参考单元的改进CFAR方法

刘 言,刘宁波,黄 勇,王中训

(1.烟台大学物理与电子信息学院,山东 烟台 264005;2.海军航空大学信息融合研究所,山东 烟台 264001)

在复杂的海洋环境中,岸基雷达和舰载雷达等海用雷达在探测舰船、掠海飞行器、航道浮标、渔船、小型游艇、浮冰等军用和民用目标时,不可避免地会受到海面散射回波即海杂波的影响。尤其在高分辨率雷达、高海况工作条件下,海杂波中频繁出现尖峰现象,且整体能量较强,易引起虚警,严重影响海上目标检测[1]。为了避免因出现误检、漏检造成损失的情况,就需要各种恒虚警(CFAR)检测器来减少虚警的出现,其中比较常见的CFAR检测器是均值类CFAR检测器[2]。在这类检测器中,它们的局部干扰功率水平估计都采用了取均值的方法,其中最经典的三种是单元平均恒虚警(CA-CFAR),单元平均选大恒虚警(GO-CFAR)和单元平均选小恒虚警(SO-CFAR)[3]。CA-CFAR是在参考单元采样服从指数分布的假设下对杂波功率水平的一个最大似然估计[4]。它在均匀高斯白噪声或均匀瑞利分布杂波背景下具有最优的检测性能,但对于复杂的海洋环境,往往强海杂波和强干扰目标的存在使得背景噪声杂乱无章,导致虚警率上升,在杂波边缘或多目标检测背景下,其检测性能下降。文献[5]通过数学推导得出结论:在CA-CFAR中,参考单元数与干扰目标数的比值小于归一化门限时,此时不管信杂比多大,CA-CFAR对主目标的检测概率始终为0,即主目标始终被遮挡。针对多目标检测背景,可以采用SO-CFAR检测器,当干扰目标只位于前沿滑窗或后沿滑窗时,它具有较好的多目标分辨能力,而对于杂波边缘环境,其性能下降,这时GO-CFAR可以保持良好的虚警控制能力,但容易在多目标环境中出现目标遮蔽现象[4]。RICKARD 等[6]提出删除均值恒虚警(CMLD-CFAR),解决多目标环境中小目标检测概率低的问题,其本质上是一种排序类CFAR处理算法。文献[7]采用蒙特卡洛仿真对CMLD-CFAR算法进行验证并将其应用到实际工程中,较为有效地解决了目标遮蔽问题。

现阶段所使用的岸基雷达或舰载雷达大部分都是相参雷达,所谓相参是指脉冲之间的初始相位具有确定性,即第一个脉冲的初相可能是随机的,但后序的脉冲和第一个脉冲之间的相位具有确定性,第一个脉冲初始相位的随机性并不影响后序的信号检测,这是提取多普勒信息的基础。所以相参雷达有准确的时钟信号,接收信号的相邻脉冲之间有很强的相关性,相位连续变化或准连续变化[8]。在使用相参雷达的前提下,针对多个强杂波或强干扰目标邻近导致检测门限虚高引起目标遮蔽,使得传统均值类CFAR检测器性能降低的情况,本文在CA-CFAR检测器的基础上,提出一种利用相位特征筛选参考单元的改进CFAR方法,通过对雷达扫描连续回波相位信息的分析,剔除若干强杂波或强干扰目标所在的参考单元,使CA-CFAR检测器得到更合适的门限,减少或避免在目标检测过程中的目标遮蔽效应。

1 CFAR检测

1.1 CA-CFAR检测原理

雷达接收的回波信号中,不仅包含着目标信号,还夹杂着各种杂波、噪声和干扰信号,同时雷达本身也可能对检测造成影响。若采用固定的门限进行检测,就会出现大量漏警或是虚警,因此需要采用自适应门限代替固定门限,CFAR方法就可以随着被检测点的背景噪声、杂波和干扰的大小自适应调整。其中,CA-CFAR是最基本的一种目标检测算法,其工作原理如图1[9]。

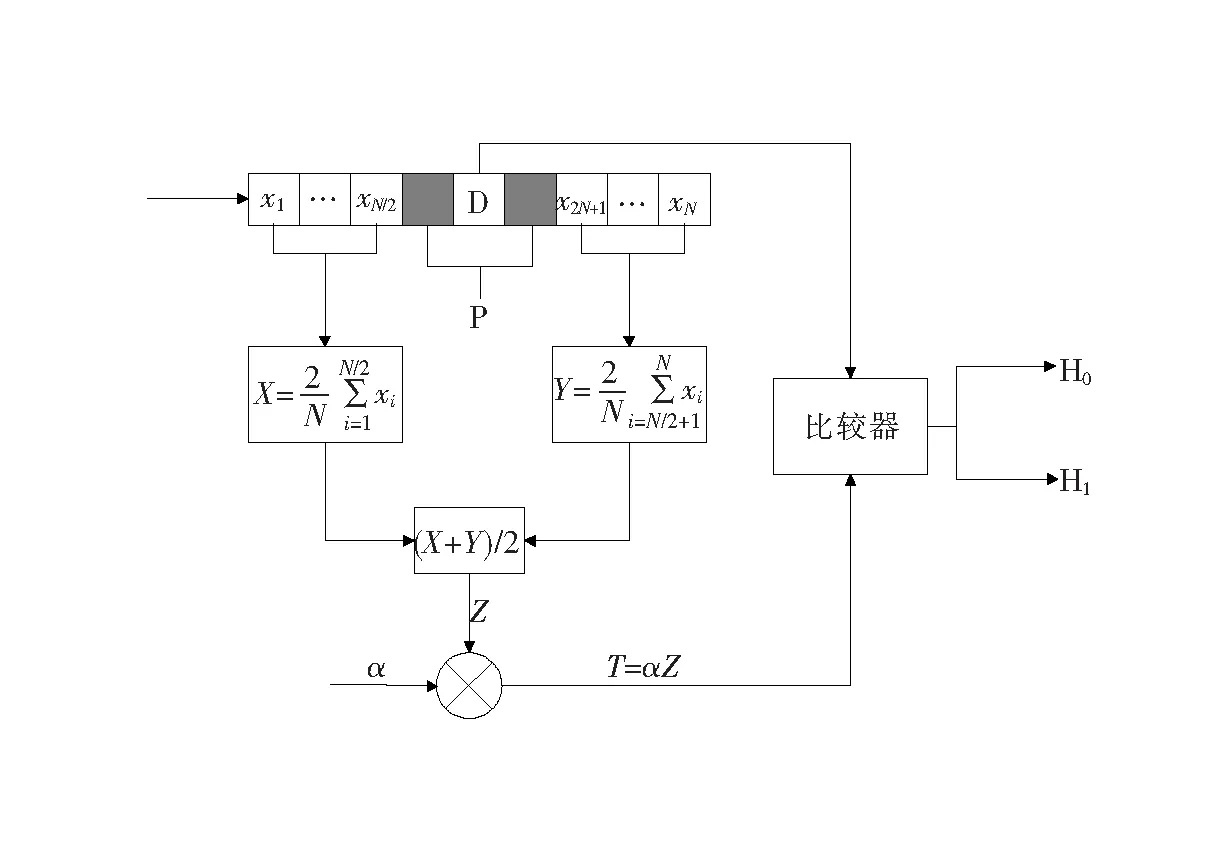
图1 CA-CFAR原理[1]

图中D表示当前待检测单元,该单元的幅值将与自适应阈值做比较;由于目标的功率可能泄露到相邻的单元中,故与目标相邻的数个单元不作为背景杂波的估计,而是作为保护单元P,在计算背景功率的时候,不包含保护单元;在D的左右两侧共取N个参考单元xi(i=1, …,N),参考单元、保护单元、待检测单元合在一起统称CFAR处理窗;接着左右两侧参考单元分别求和取平均来估计待检测单元的背景杂波功率Z;在给定的预期虚警概率PFA下,Z与标称化因子α相乘得到检测门限T,若待检测目标幅值大于T,则认为发生事件H0,即该检测单元是目标,否则发生事件H1,即该检测单元不是目标。

海杂波是由天线波束区内大量散射单元的散射信号叠加而成,因此可以近似认为海杂波是高斯分布的,其杂波回波经幅度检波后,幅度概率密度函数也符合瑞利分布[10-11],其概率密度函数为

(1)

由图1可知,待检测单元的背景杂波功率为

将得到的待检测单元D的背景杂波功率与标称化因子α相乘,即可得到门限值T,表示为

由此可以通过估计最终得到门限值T表达式为

令c=α/N,与式(1)联立则可以计算出门限值T的概率密度分布,表示为

再通过奈曼-皮尔逊准则,将得到的虚警概率的概率密度分布求积分,即可得到虚警概率,最终结果表示为

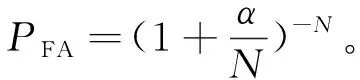
(2)

针对式(2),对于给定的预期虚警概率,所需的标称化因子可通过解式得

需要指出,PFA不依赖于实际干扰噪声功率的大小,仅仅和参与平均的临近单元样本N及标称化因子α有关。因此,CA-CFAR表现出CFAR的特点。

1.2 CA-CFAR的局限

CA-CFAR的概念受限于两个基本的假设: (1)目标是独立的,目标间至少一个参考窗的长度,以使得参考窗内不会有同时存在两个目标的可能;(2)参考窗内的所有干扰数据都是独立分布的,且和包含目标的单元内的干扰同分布,也就是说,干扰是均匀的。

在复杂的海洋环境中,实际情况往往会违反其中一个或两个条件,当待检测目标周围有两个或多个目标时,参考单元的目标回波功率可能超过了周围的干扰功率,杂波功率估计值就会被提高,CFAR的门限因此会被抬升,从而CFAR检测器就无法检测到该目标,发生目标遮蔽现象。等效地,为了获得给定的检测概率期望值,则需要更高的信杂比[4]。图2是一个发生遮蔽效应的实例,设定参数PFA的期望值为10-4,参考单元N取32个,待检测目标左右各取一个单元作为保护单元,在200个距离单元中,在位于第70个、第78个距离单元上分别加入信杂比为15、20 dB的两个目标。如图2,当信杂比为15 dB的第一个目标处于待检测单元时,信杂比为20 dB的第二个目标提高了自适应阈值的估计值,导致第一个目标无法被检测到,使检测器发生漏检;另一方面,信杂比为15 dB的目标足够小,无法影响到后者的检测情况,故成功检测到第二个目标。

图2 目标遮蔽实例

2 CFAR方法的改进

CA-CFAR检测器在对海进行目标检测时,可能因陆地岛屿、强干扰目标或者海尖峰的存在,使得海面杂波背景变得严重非均匀,不符合CA-CFAR检测器使用的前提条件,同时这些干扰因素可能意外抬高检测门限、降低检测性能,造成检测器的漏检。为避免这种情况,可以把待检测目标附近的强干扰目标或强海杂波筛选后剔除,使得海杂波的幅度概率密度函数更符合瑞利分布,背景杂波功率也不受干扰目标的影响;同时,采用相参雷达对海面目标连续检测时,往往这些陆地岛屿、强干扰目标或海尖峰的相位信息在一定置信度允许的情况下可视为线性。

基于此,本文针对使用相参雷达的情况,在CA-CFAR的基础上提出利用相位特征筛选参考单元的改进CFAR方法。从实际角度出发,改进CFAR是通过筛选维护参考单元空间的均匀性,使参考单元符合CA-CFAR的背景要求,而不是改进CFAR算法的生成方式,故改进CFAR的门限T、虚警概率PFA与标称化因子α的推导过程与“1.1”小节的CA-CFAR算法一致。

2.1 参考单元线性判断模块

海上目标检测一般使用的是相参雷达,故可以用相位来获取目标的一些信息[12]。取参考单元中某一个距离单元的10个或16个脉冲回波,获取它们的相位信息,通过一元线性回归的方法,判断其相位线性度的好坏。由于实际接收的雷达回波信号可能会存在难以预测和控制的随机相移,所以我们需要对大量实测数据进行测试,找出合适的置信度,在置信度允许的范围内判断相位线性度的好坏。通过Matlab中的Regress函数可得到模型统计量[13],根据R2统计量及显著性概率P值的大小来判断相位之间是否具有线性关系。

本文从文献[1]、[14]分享的雷达对海探测数据中,下载大量实测扫描数据对模型统计量的参数设置进行分析,实测数据表明:当选取参数R2值大于0.90且P值小于0.05的默认显著性水平作为判断线性相关依据时,由于剔除了过多的相位线性度好的参考单元,导致门限降低,容易产生虚警,影响检测性能;当选取参数R2值大于0.98且P值小于0.05的默认显著性水平作为判断线性相关依据时,由于剔除的参考单元较少,相比于CA-CFAR检测器检测性能提高较小,意义不大;经过大量实测数据测试,综合实际情况因素,当R2值大于0.95且P值小于0.05的默认显著性水平时,检测性能提高的同时也尽可能地避免虚警的出现,故可据此参数来判定该参考单元的相位特征是否为线性相关并是否需要剔除。图3是用两组同一距离单元的连续10个脉冲回波进行测试,图3(a)求得模型统计量R2值0.998 1大于0.95接近于1,P值0.013 3小于0.05的默认显著性水平,因此可判断为线性;图3(b)求得R2值0.834 3小于0.95,P值0.250 7大于0.05的默认显著性水平,因此可判断为非线性。

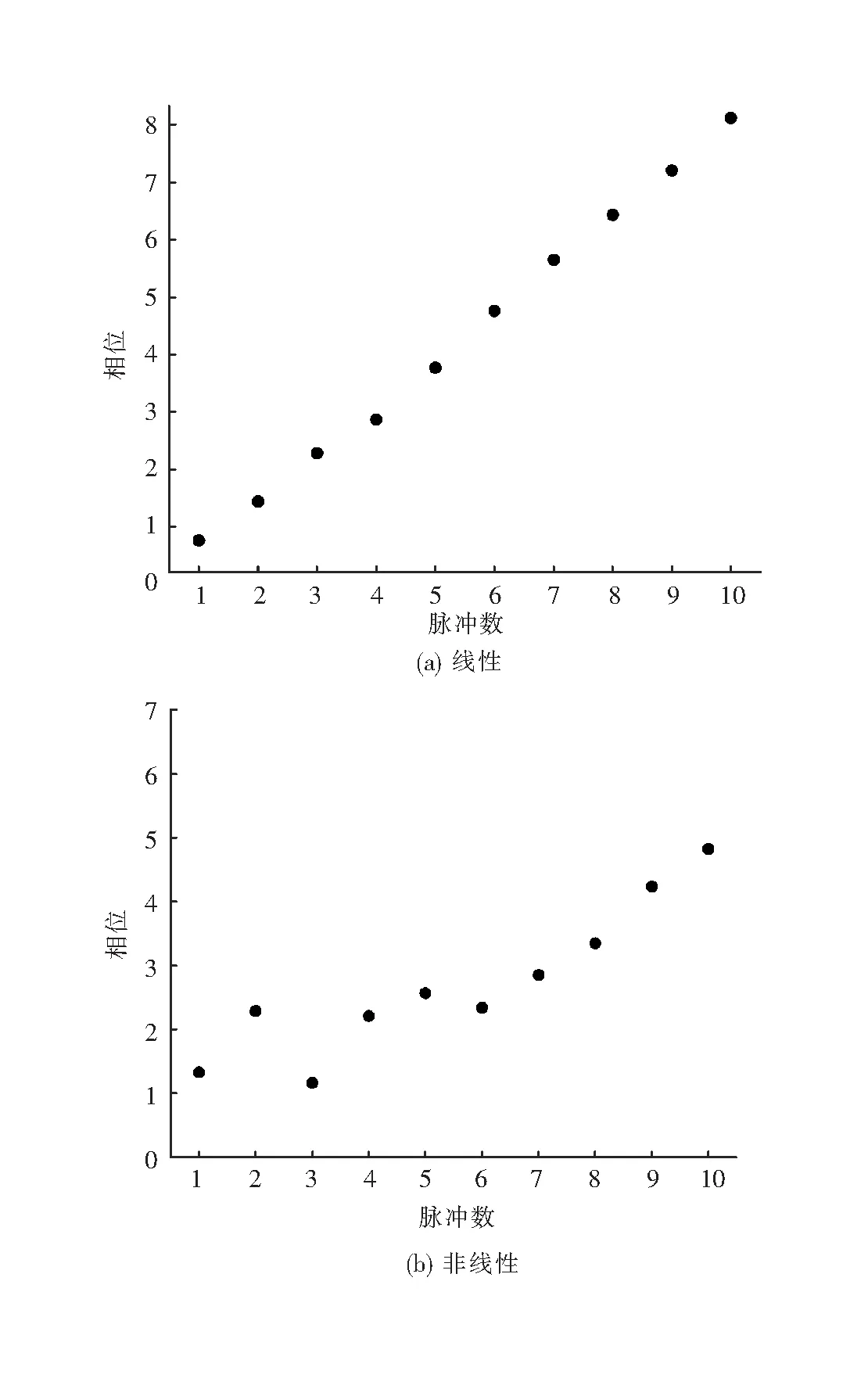
图3 相位特征线性判断

2.2 剔除相位特征呈线性的参考单元模块

在相参雷达中,若连续脉冲回波在同一距离单元的相位线性度很好,则在这个距离单元上就可能是目标、强杂波、干扰目标或陆地杂波。为了获得更合适的门限,就需要将待检测单元附近线性度较好的参考单元剔除。改进算法的原理如图4。

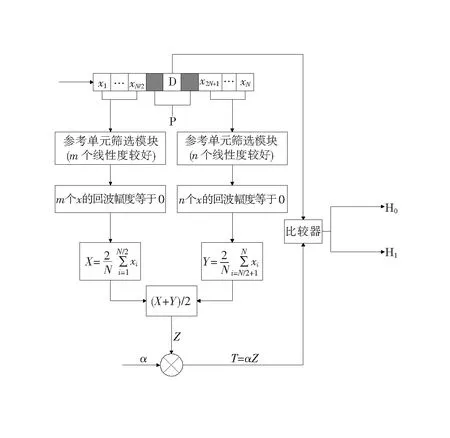
图4 改进算法原理

图4中待检测单元D、保护单元P、参考单元N选取规则与经典CA-CFAR一致,不同的是在左右两侧参考单元选取中,通过参考单元线性判断模块筛选出线性度好的参考单元并将其回波强度变为0,在滑窗的过程中统计左右两侧回波强度等于0的个数m、n,然后将N个参考单元求和取平均,此时的均值实际是N-(m+n)个参考单元的均值,也就是新的背景杂波功率估计值Z,再将Z与标称化因子α相乘得到新的门限值,最后与待检测单元D做比较判断此距离单元是否存在目标。假设一开始N取32个,左右两边各16个,在模型统计量的相位线性度判断下,剔除线性度好的强目标或强杂波,此时参考单元实际个数可能变为24个,用剩余的参考单元得到的背景杂波功率估计值要远比32个参考单元得到的背景杂波功率估计值合适。

3 仿真数据测试

3.1 均匀单目标背景环境

图5是在均匀杂波背景、PFA=10-6、N=32的情况下,均值类CFAR(CA-CFAR、GO-CFAR、SO-CFAR)、CMLD-CFAR与改进CFAR检测器对单一目标检测的性能曲线(ROC曲线)[15]。图5中opt为特定信噪比对应的最优检测,由于只有一个目标且改进的CFAR检测器仅仅对强杂波或强干扰目标有筛选剔除作用,故改进的CFAR检测器与CA-CFAR检测器的检测性能一致,在目标信杂比接近19 dB时达到80%的检测概率[4],利用相位特征筛选参考单元的检测器没有丧失原有的检测功能;CMLD-CFAR由于在检测过程中删除部分参考单元,相较于CA-CFAR有较小的信杂比损失;SO-CFAR在多目标检测时有较好的检测性能,而对于单目标检测信杂比损失较大。

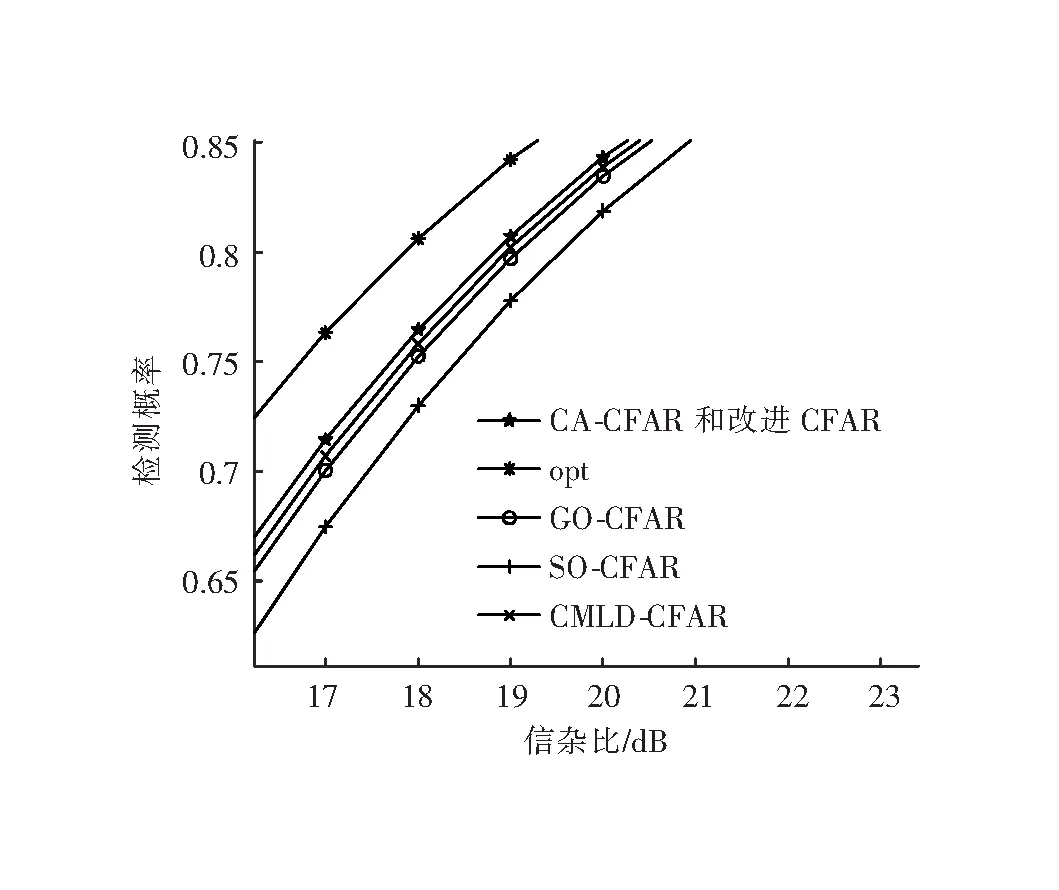
图5 均匀单目标ROC曲线

3.2 多目标背景环境

在多目标背景的检测中,往往会出现幅度高的目标把幅度低的目标遮蔽的现象,使得检测概率降低[16]。图6(a)是仿真出的两个靠得比较近的大小目标,大目标功率值高出小目标功率值5 dB,平均杂波功率在20 dB左右,其中小目标所在位置的相位特征线性度较好。图6(b)是CA-CFAR检测器和利用相位特征筛选参考单元的改进CFAR检测器在PFA=10-6、N=32时对功率值较大目标(大目标信杂比由0 dB逐步增加到30 dB,小目标信杂比随之增加)检测的ROC曲线。

图6 双目标环境

图6可以看出,当目标信杂比小于5 dB时,两种检测器检测性能相当,且两者的检测性能都随着信杂比的提高而增强,当系统要求检测概率达到50%时,CA-CFAR检测器需要目标达到17 dB,而改进的CFAR检测器由于将小目标所在的参考单元剔除,得到了一条更适合的门限,仅需目标达到14 dB即可被检测出来。

图7(a)是在杂波的第80、88、98、104距离单元仿真出四个靠得很近的目标,其中第80、98距离单元目标的功率值足够大,相位线性度较好,可以被改进算法筛选剔除。从均值类检测器中选用对多目标检测效果最好的SO-CFAR检测器与改进CFAR检测器做比较,结果用A显图展示,如图7(b):SO-CFAR能够在众多目标中将大多数目标检测出来,但由于第88距离单元的目标功率值太小,未能成功检测;而改进CFAR对参考单元进行了筛选,成功检测出所有目标。这表明改进CFAR在多目标检测仿真实验中能够展现其优势。

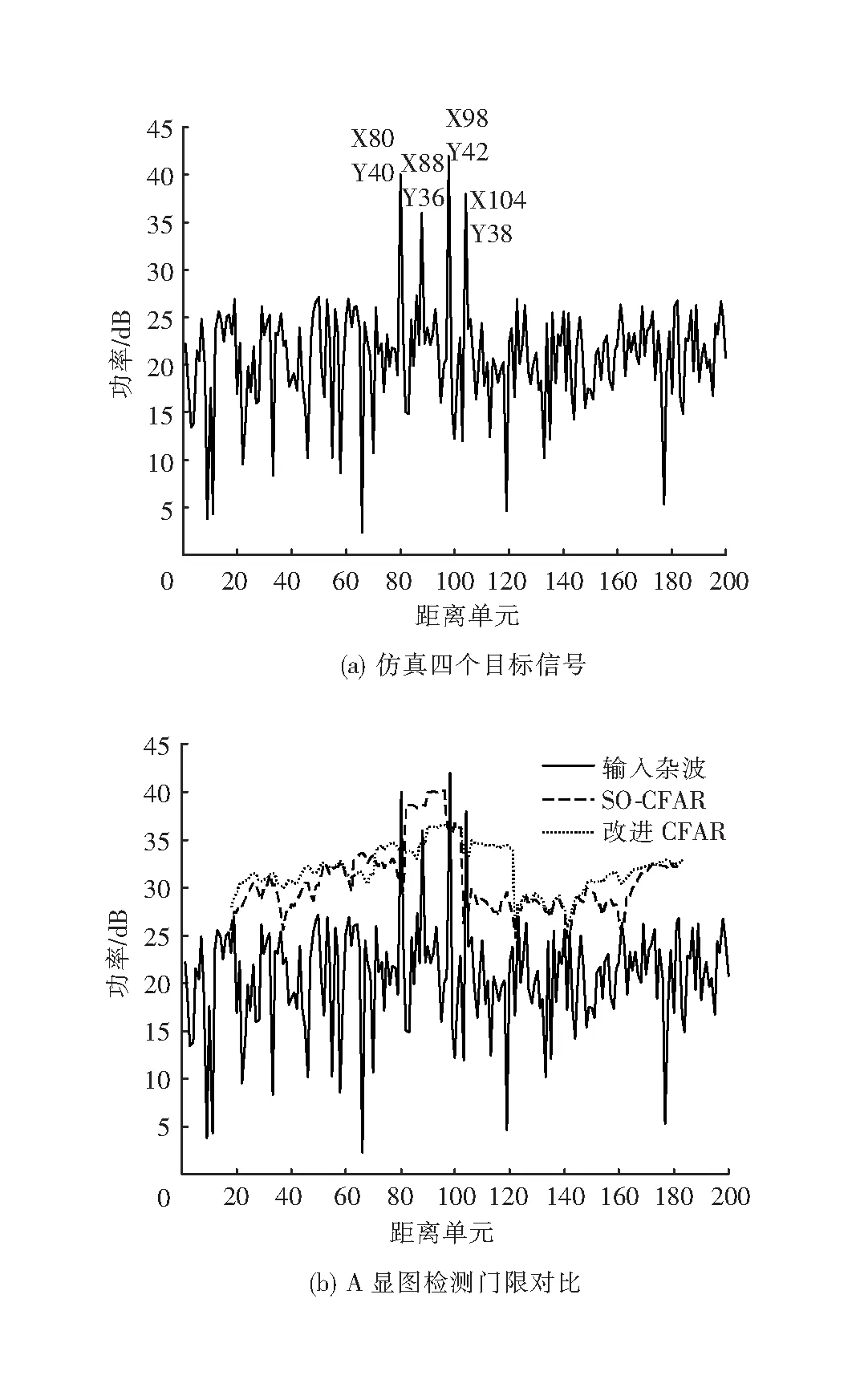
图7 多目标环境

3.3 杂波边缘环境

典型的杂波边缘环境一般是海陆交界的地方,在距离维上发生能量突变,使得处于低杂波边缘的目标被判定为高功率的杂波,造成漏检;也可能将高功率区域的边缘杂波误认为目标,造成虚警[17]。这里仿真了杂波边缘的环境,并在低功率区第88和95距离单元添加两个目标,其中左侧目标的相位线性度较好,如图8(a)所示;图8(b)选用对杂波边缘环境检测效果较好的GO-CFAR检测器与改进的CFAR检测器做对比,在N=32、PFA=10-6情况下得到的两条门限,这两个检测器都成功检测到了第一个目标,但由于大目标的影响,GO-CFAR检测器无法成功检测到第二个目标;改进的CFAR检测器通过对参考单元选取的改进,降低了目标处的门限,成功检测到了第二个目标。在杂波边缘环境中,改进算法与GO-CFAR都有着较好的检测性能,但当杂波边缘环境中存在多个目标时,改进的CFAR比GO-CFAR检测性能更好。

图8 杂波边缘环境

综上所述,利用相位特征筛选参考单元的改进CFAR检测器在均匀单目标杂波背景下,由于没有需要剔除的参考单元,其检测性能与CA-CFAR基本一致且没有丧失原检测器的功能;在多目标背景和杂波边缘背景下的检测性能要优于其他均值类检测器,至于不同背景下检测性能提升了多少,要根据实测数据的相位特征来断定,具体情况需具体分析。

4 实测数据测试

为进一步验证改进CFAR检测器的性能,从文献[1]、[14]分享的实测数据中,下载了一组扫描数据,该组数据是2239×2224的矩阵,其中每一行代表方位/脉冲,每一列代表距离单元,并记录了雷达扫描范围259.445°至0°至125.992°的信息。

这里任取十个连续回波的数据进行测试,在方位71.781°,距离单元1501、1784和1791附近有若干个船只,N取64个,由于船只宽度等因素,保护单元左右各取4个,PFA取10-4,改进的CFAR检测器中,由R2值是否大于0.95且P值是否小于0.05作为线性判断的标准,测试结果如图9。从实测数据图9(a)来看,在1501距离单元附近,由于主目标幅值足够大且邻近干扰目标幅值较小,CA-CFAR与改进的CFAR都能检测出目标船只,但后者只需要更低的功率值就可以检测到;位于1784与1791距离单元附近,由于主目标附近有强海杂波或强干扰目标,采用CA-CFAR检测器就造成了目标遮蔽现象, 而采用改进的检测器避免了这种情况,成功检测出目标。多目标检测效果较好的SO-CFAR与改进CFAR测试结果如图9(b),两者都成功检测出了目标,但由于都降低了门限,可能存在虚警现象,也有一定不足。

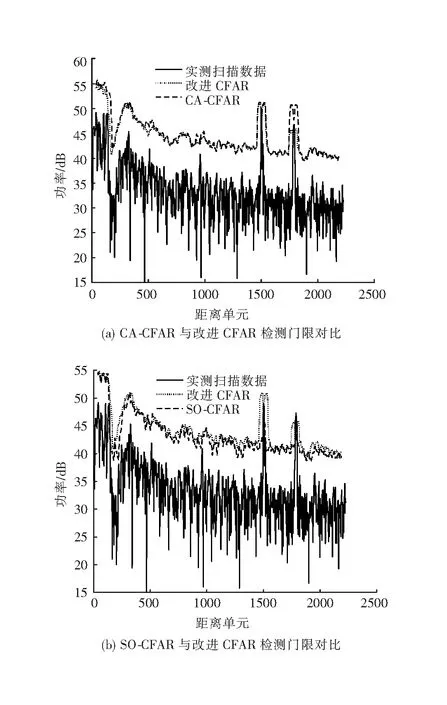
图9 实测数据测试结果

进行海上目标检测时,往往存在多个邻近目标,当待检测目标较强时,也就是大目标附近有许多小目标,这时小目标落到参考单元里面,由于小目标强度较弱,相位线性度可能不好,导致无法剔除,但小目标本身对参考单元空间均匀性影响较小,对背景杂波功率影响不大,能够正常检测出大目标;当待检测目标较弱时,也就是小目标附近存在许多大目标,这时大目标落到参考单元里面,它的相位线性度是比较好的,可以剔除,那么剩余的参考单元的空间均匀性肯定比大目标存在时的空间均匀性好很多,背景杂波功率会更合适。从这个角度来说,一定程度上能解决大目标附近的小目标检测问题,包括大目标附近的小目标检测或者大目标附近有强地杂波、杂波边缘的这种情况也类似。实际上这是利用了一个先验信息,这个先验信息是我们从大量实测数据中得到的:无论是强杂波还是强目标,它的相位线性度都是比较好的。

5 小 结

由于海面环境复杂多变,多目标环境与海陆交界处采用CA-CFAR容易出现目标遮蔽、漏检的现象。针对这一问题,本文提出了一种利用相位特征筛选CA-CFAR参考单元的改进算法,剔除相位线性度好的强杂波或强干扰目标所在距离单元,使得检测背景更符合均值类CFAR的使用前提。经过仿真数据和实测数据的分析验证可知,改进算法能够在多目标环境与杂波边缘环境下检测到CA-CFAR无法检测的目标,有效解决目标遮蔽问题且不丧失原有的检测性能,相比其他均值类CFAR检测性能有所提升,表明了改进CFAR算法的有效性。此算法使用的前提是需要对已知海域进行大量实测数据分析,得出相位特征信息,且算法的计算量要比其他均值类CFAR复杂,还有一定的改进空间。