关于有限群的非循环真子群的自正规性和非正规性

田云凤,史江涛,刘文静

(烟台大学数学与信息科学学院, 山东 烟台 264005)

1 背景知识及主要结果

在文献[2]中,GIORDANO刻画了每个非正规子群皆自正规的群的结构。对于p-群,文献[3]和[4]完全分类了每个非循环子群皆正规的p-群。 作为文献[3]和[4]的推广,文献[5]和[6]决定了所有非交换子群皆正规的群。

考察非循环p-子群或自正规或正规的群,SHI在文献[7]中证明了下述结论:

定理1[7]设G是群,p是|G|的最小素因子,令P∈Sylp(G)则

(1)如果G的每个非循环p-子群都在G中自正规,则G为p-幂零;

(2)如果G的每个非循环p-子群都在G中正规,则G为p-幂零或P正规于G;

作为上述文献的推广,考察超可解的非循环子群皆自正规的群,KUTNAR等在文献[8]中得到了:

定理2[8]设G是非循环群,则G的每个超可解的非循环子群皆自正规当且仅当G为下列群之一:

(1)Zp×Zp,p是素数;

(2)四元数群Q8;

定理3[9]设G为至少含一个非循环真子群的群,则G的每个非循环真子群皆非正规当且仅当G为下列群之一:

(1)G/Φ(G)是非交换单群,且满足Φ(G)=Z(G)是循环的,其中Φ(G)是G的Frattini子群,Z(G)是G的中心;

文献[9]定理1.3指出:对比文献[8]定理1.2中的分类和文献[9]定理1.1中的分类,可得下述结论:

定理4[9]设G为至少含一个非循环真子群的可解群,则G的所有非循环真子群皆非正规当且仅当G的所有非循环真子群皆自正规。

作为上述定理4的改进和推广,不需要用到文献[8]定理1.2和文献[9]定理1.1,本文直接证明了下述结论成立:

定理5 设群G至少含一个非循环真子群,则G的每个非循环真子群皆自正规当且仅当G为每个非循环真子群皆非正规的可解群。

2 定理5的证明

证明必要性:因为群G的每个非循环真子群皆自正规,自然有G的每个非循环真子群皆非正规,下面只需证明群G可解。

令P1′为M的Sylowp1-子群。对任意2≤i≤s,令Pi为M的Sylowpi-子群,则Pi也是G的Sylowpi-子群。由于M循环,知M=P1′×P2×…×Ps。因为M正规于G,有P1′正规于G。于是G=MP1=(P1′×P2×…×Ps)P1=(P2×…×Ps)P1,其中P2×…×Ps循环。

如果P1正规于G,则G是幂零群。于是G的每个极大子群皆正规,由题设知G的每个极大子群都循环,此时G不存在非循环真子群,与题设矛盾。故P1不正规于G。

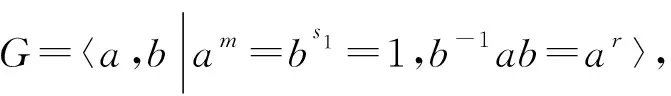
令x=bj2(at)i2,j2和i2是正整数。因为〈bh〉=〈bx〉,则存在正整数u,使得:bh=(bx)u=(bu)x。于是a-i1b-j1bbj1ai1=a-ti2b-j2bubj2ati2,即a-i1bai1=a-ti2buati2。把等式两边同时左乘b-1后,得等式(1):

b-1a-i1bai1=b-1a-ti2bbu-1ati2。

(1)

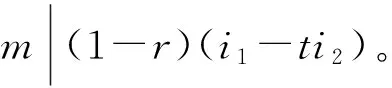
由h的任意性得NG(Hg-1)≤Hg-1,从而Hg-1=NG(Hg-1),即Hg-1=(NG(H))g-1。因此有H=NG(H),说明群G的每个非循环真子群都自正规。证毕。