垃圾渗滤液用厌氧反应器布水器CFD数值模拟

田丽森 赵 金 赵永志 杨 恒 刘少非 王彦芳 王海红 郭天宇

(中国恩菲工程技术有限公司, 北京 100038)

0 前言

厌氧反应器是一种高效的废水处理装置,主要利用厌氧微生物的自身代谢过程将废水中的有机物转化为无机物和少量细胞产物,从而达到废水处理的目的[1]。目前,在垃圾渗滤液、屠宰废水等高浓度废水处理领域,通常采用的厌氧反应器有升流式厌氧污泥床反应器(UASB)、厌氧颗粒污泥膨胀床反应器(EGSB)、厌氧内循环反应器(IC)等[2-3]。无论哪一种反应器,布水器均是它们正常运行的关键因素。具体地,布水器使待处理的废水进入厌氧反应器的底部,使废水与污泥充分接触,通过厌氧微生物的代谢降解作用,使废水中的大部分有机污泥物转化为沼气,小部分转化为污泥、沼气、水、泥混合物等[4]。

布水器的优劣直接影响废水处理效果。目前应用比较广泛的厌氧反应器布水器主要有枝状、环状和网状三种。因此利用CFD数值模拟技术对三种布水器进行模拟[5-7],通过改变布水器结构形式及分布器出水角度等主要参数,分析反应器内部的流动状态,基于充满度、死角区面积的对比,为反应器布水方式的选择提供参考,推动自主研发设计高效厌氧反应器的应用进程。

1 构型选取及参数设置

根据工程经验,选取了枝状结构、环状结构及网状结构等三种不同的布水器进行模拟仿真分析,它们分别对应后文的方案1、方案2和方案3,其中方案2环状结构又根据布水支管的角度不同细分为3个小方案。通过对不同结构形式布水器的布水过程进行数值仿真和分析,确定最佳的布水器结构,避免死角,减少污堵结垢,并进一步对布水器结构优化提出改进建议,从而提高垃圾渗滤液厌氧反应器的生产效率。

厌氧反应器内布水器主要操作参数见表1。

布水器数值仿真中采用的数学方法、模型以及相关参数的选择见表2。

表2 布水器数值仿真数学方法和模型确定

1.1 布水器几何结构

方案1枝状布水器几何结构以及各部分尺寸如图1所示。枝状布水器共有12根支管,其中6根开8个孔(两种直径的孔,每种4个,孔径分别为12 mm 和10 mm),另外6根开有12个孔(三种直径的孔,每种4个,孔径分别为12 mm、10 mm和8 mm),两种支管相间布置,孔的分布如图2所示。

图1 方案1枝状布水器结构

图2 枝状布水器支管出孔分布情况

方案2环状布水器主管为圆环形,支管共40根,均匀分布在主管圆环上,每根支管间的圆心角为9°,支管与圆环主管轴线夹角有3种,分别为30°、60°和90°,入口管有两根。方案2环状布水器几何结构如图3所示。

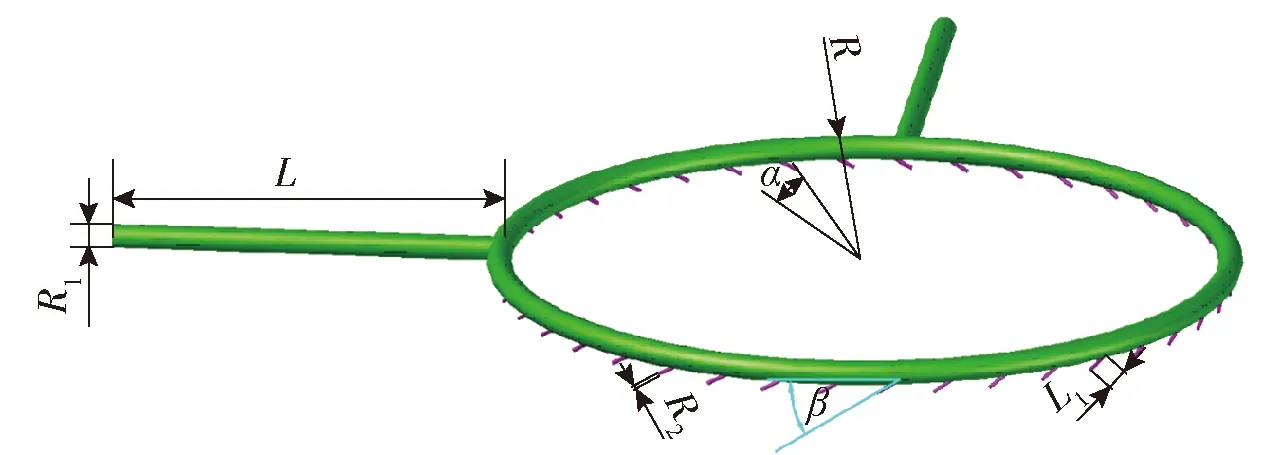
L-进水主管长度; L1-布水支管长度; R-环状布水器主管半径; R1-进水主管管径; R2-布水支管管径; α-布水支管间夹角; β-布水支管与布水主管夹角图3 方案2环状布水器几何结构

环状布水器共包括3个小方案,各方案几何尺寸见表3。

表3 方案2各子方案结构参数

方案3网状布水器几何结构如图4所示。入口管以及各支管直径均为32 mm,共有64个出口。按图4所示给各出口编号,以方便分析模拟结果,并将方案3所示布水器中的分流结构分为如图4所示的三级。入流主管先分为两根一级入流支管,每根一级入流支管对应的结构为一级分流结构;一级入流支管再一分为二,得到两根二级入流支管,二级入流支管对应的为二级分流结构。方案3共有一级分流结构2个,二级分流结构4个,三级分流结构16个。

图4 方案3网状布水器几何结构

1.2 布水器计算网格

方案1计算域离散为如图5所示的四面体网格。网格质量见表4。

图5 方案1枝状布水器计算网格

由表4可知,网格划分合理,网格质量好。

方案2中3个小方案计算域离散为如图6所示的四面体网格。网格质量分别见表5。

图6 方案2环状布水器计算网格

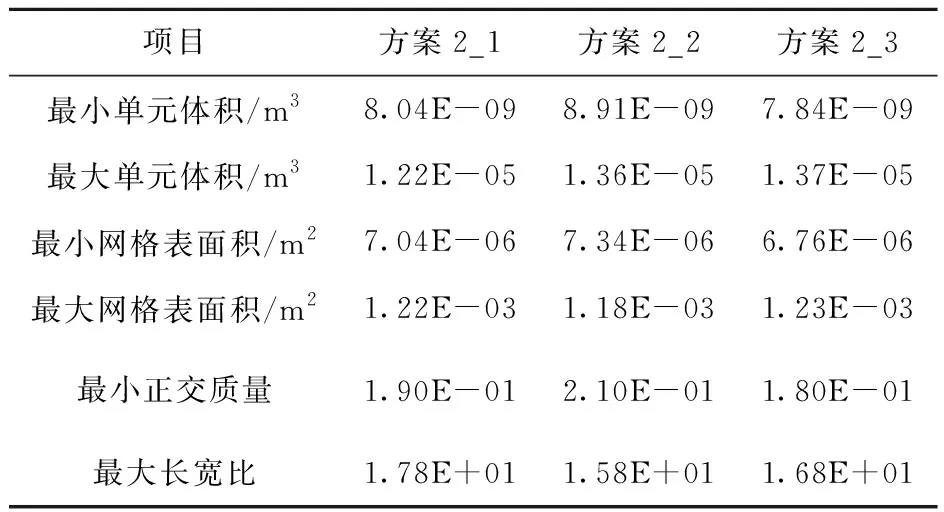
表5 方案2网格质量

由表5可知,网格划分合理,网格质量好。

方案3计算域离散为如图7所示的四面体网格。网格质量分别见表6。

图7 方案3网状布水器计算网格

表6 方案3网格质量

由表6可知,网格划分合理,网格质量好。

2 数值仿真结果分析

2.1 方案1枝状布水器数值仿真

为方便分析模拟结果,将各支管以及支管上的出孔进行编号,如图8所示。图9为XY平面上速度大小分布云图。

图8 各支管及出孔编号情况

图9 XY平面上速度分布云图

如图9所示,枝状布水器支管中的速度分布呈很好的中心对称性;越靠近中心,支管中的速度越大;随着径向位置增大,出水孔数量逐渐减少,流量减小,支管内的流速也逐渐减小。

入口压力为235 440 Pa和392 400 Pa时各出口流量分别如图10(a)和10(b)所示。由图10可知,两种孔数管相应位置的出口流量相差很小;同一支管上,孔径相同的出口流量基本相同;孔数量为8的支管所有出口总流量的平均值为8.304 kg/s,孔数量为12的支管所有出口总流量的平均值为10.41 kg/s,这是因为由于开孔数量增多,流体阻力减小,导致多孔支管的流量增大,即孔径大的出口流量并没有因离中心管远而降低。

图10 方案1枝状布水器各出口流量

将布水器按图2所示分为6个相同的小单元,并将该小单元按分为O、P和Q三个区域。根据数值仿真结果,P区域的单位面积流量比O区域高56.6%,比Q区域高40.2%。

支管12上的出口1、5和9的速度矢量分布如图11所示。

图11 支管12上出口1、5和9速度矢量分布

由图11可知,位于支管12末端的1出口速度矢量分布无明显规律,比较杂乱,支管轴线一侧的速度明显大于另一侧的速度;出口5的位置约位于支管中间,速度矢量分布也不均匀,靠近来流方向区域的速度矢量略显杂乱,不与出口面垂直,且速度大小明显偏小;出口9比较靠近布水器主管,速度矢量基本都与出口平面正交,但仍呈现越靠近来流方向速度越小的特点。

2.2 方案2环状布水器数值仿真分析

2.2.1 支管与主管轴线夹角为30°

以两入口夹角平分线以及两根入口管延长线将布水器圆环主管分成如图12所示的A、B、C和D四部分。当入口压力为235 440 Pa时,由入口1和入口2进入的流体在各出口的分布情况如图12所示。由图12可知,由入口1进入的流体主要从A和B两段圆弧上的出口流出;而由入口2进入的流体则主要由C和D两段圆弧上的出口流出。

图12 布水器内流线分布

图13为XY平面上环形布水器内部速度场分布。由图13可知,离两个入口越近,流体发分布器主管截面的速度越大、流量越大。

图13 布水器内XY平面速度分布

图14为出口7和出口27的速度矢量。对于出口27,越靠近来流方向,速度越小;对于出口7,越靠近来流方向,速度越大。

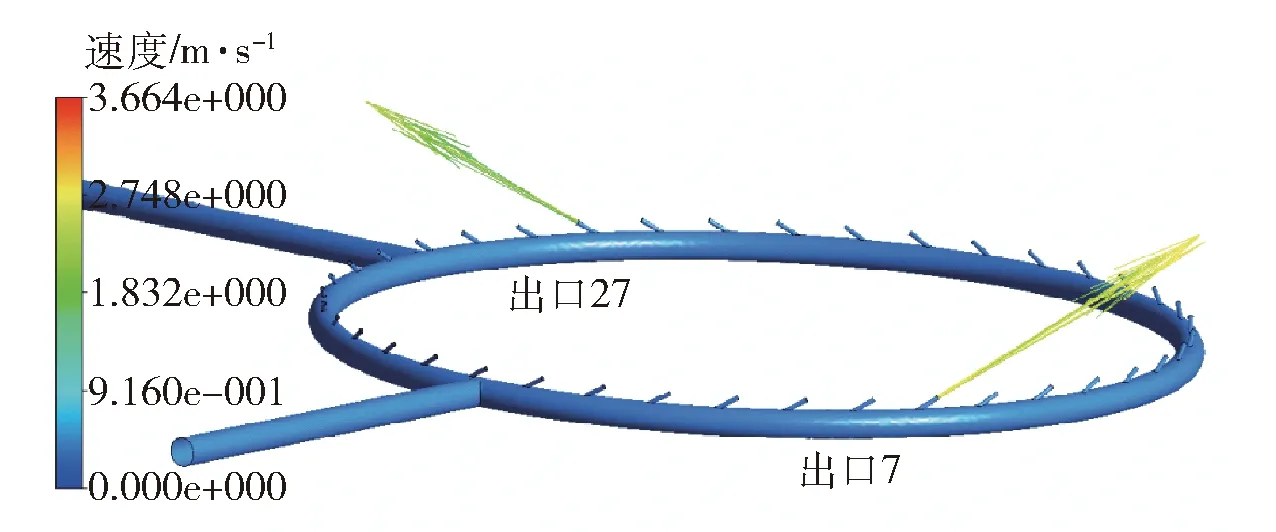
图14 出口7和27速度矢量分布

方案2_1流体分布器各出口流量如图15(a)所示。按图12所示将布水器主环管分为A、B、C和D四段。A段对应的出口编号为31～35,B段圆弧对应的出口编号为16～30,C段对应的出口编号为1～15,D段对应的出口编号则为36～40。

图15 方案二不同结构和入口压力下各出口流量分布图

1)虽然A、B段与C、D段在几何上完全对称,但各对称位置上出口流量并不相等。

2)C段和D段对应的出口流量之和明显大于A和B段对应的出口流量之和,前者超出后者约8%,所有支管流量的标准差为0.17 kg/s。

3)流体由入口管1进入到B段后,要想从B段上的支管流出,其速度方向要发生很大改变,因而流体从该段支管流出阻力加大。

4)流体由入口管1进入A段后,某时刻的速度方向与支管夹角较小,流体易于从支管中流出,A段各支管流量均值明显大于B段各支管流量均值。

5)从入口管2进入的流体在各出口的分布情况与入口管1类似。

改变两个入口压力为392 400 Pa,对布水器内流场重新进行模拟,得到各支管流量如图15(d)所示。与图15(a)对比可知,改变入口压力后,各出口流量几乎没发生变化。

2.2.2 支管与主管轴线夹角为60°

将支管与环形主管轴线夹角由30°变为60°,入口压力为235 440 Pa时,各支管流量如图15(b)所示。A段+B段支管流量之和与C段+D段支管流量之和差异仍比较明显,后者比前者超出约6%,各支管流量标准差为0.136 kg/s。与支管和环形主管轴线夹角为30°时相比,两者差异明显减小。

图16为出口7和出口27的速度矢量。由图16可知,对于出口27,越靠近来流方向,速度越小;对于出口7,越靠近来流方向,速度越大。

图16 出口7和27速度矢量分布

同理,改变入口压力为392 400 Pa,得到各支管流量如图15(e)所示。对比图15(b)可知,两种入口压力下,各支管流量几乎没有变化,再次证明了入口压力不是影响各支管流量的主导因素。

2.2.3 支管与主管轴线夹角为90°

将支管与环形主管轴线夹角由30°改为90°,入口压力为235 440 Pa时,得到各支管流量如图15(c)所示。

与以上几个方案相比,该方案A段+B段支管流量之和与C段+D段支管流量之和差异继续减小,前者超出后者约5.5%。

图17为出口7和出口27速度矢量分布情况。由图17可知,出口7圆环内侧速度小,而出口27情况相反。

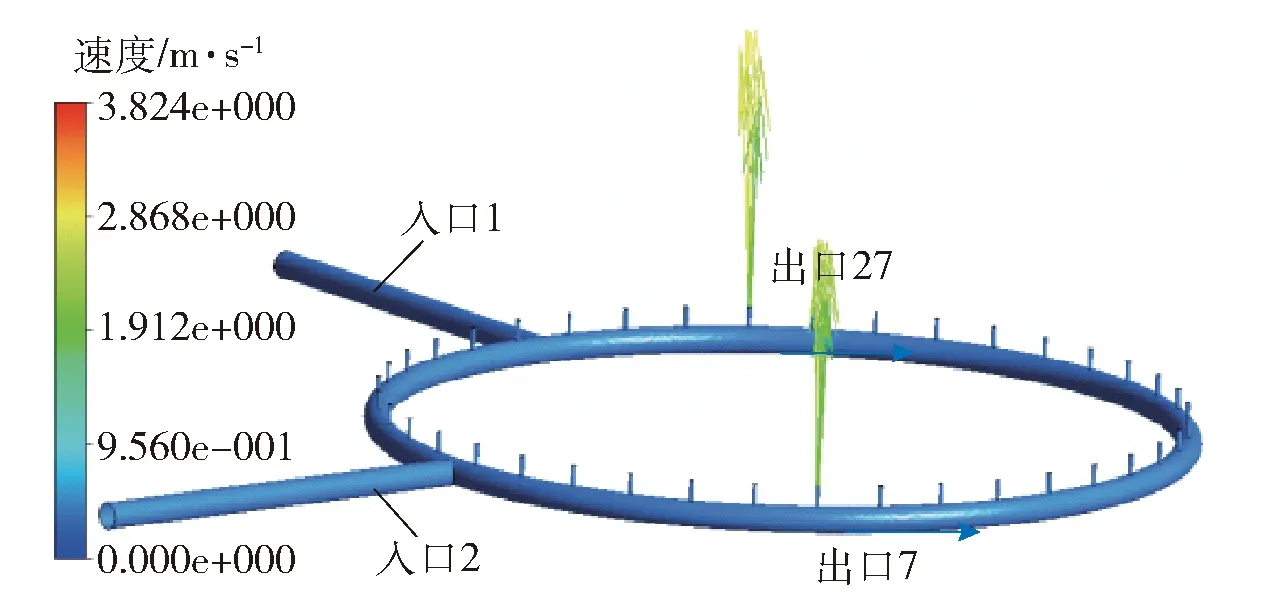
图17 出口7和出口27速度矢量分布规律

2.2.4 三维螺旋环流的形成

以方案2支管与环形主管夹角等于60°的情况为例,模拟支管与环形主管不垂直时布水器射出的流体在反应器内的分布状态。将反应器计算域几何结构进行简化,其几何结构和计算网格如图18所示。

图18 布水器和简化的反应器几何结构和计算网格

数值模拟得到布水器以及反应器内流线分布形态如图19～21所示,布水器射流以环形旋转辐射的形式进入反应器内,在反应器壁面作用下向上运动。

图19 流体进入布水器后运动轨迹

图20 Z=-0.25 m的XY平面上流线分布

图21 环状反应器内部流线分布

环形旋转射流带动反应器内原有流体运动。在布水器送入的流体带动下,反应器内流场发生改变,反应器内流场除发生水平方向的旋转流外,还会发生二次环流:以布水器出口围成的圆为界,圆内部流体向下、向外运动;圆外部流体向上、向外流动,容器中心处缺失的流体则由上部中心处的液体补充,形成三维旋转环流,从而改善了布水器的分布均匀性,弥补了布水器出口分布不均的缺陷。

2.3 方案3网状布水器数值仿真

当入口压力为235 440 Pa时,方案3网状布水器数值模拟得到的各出口流量如图22所示。

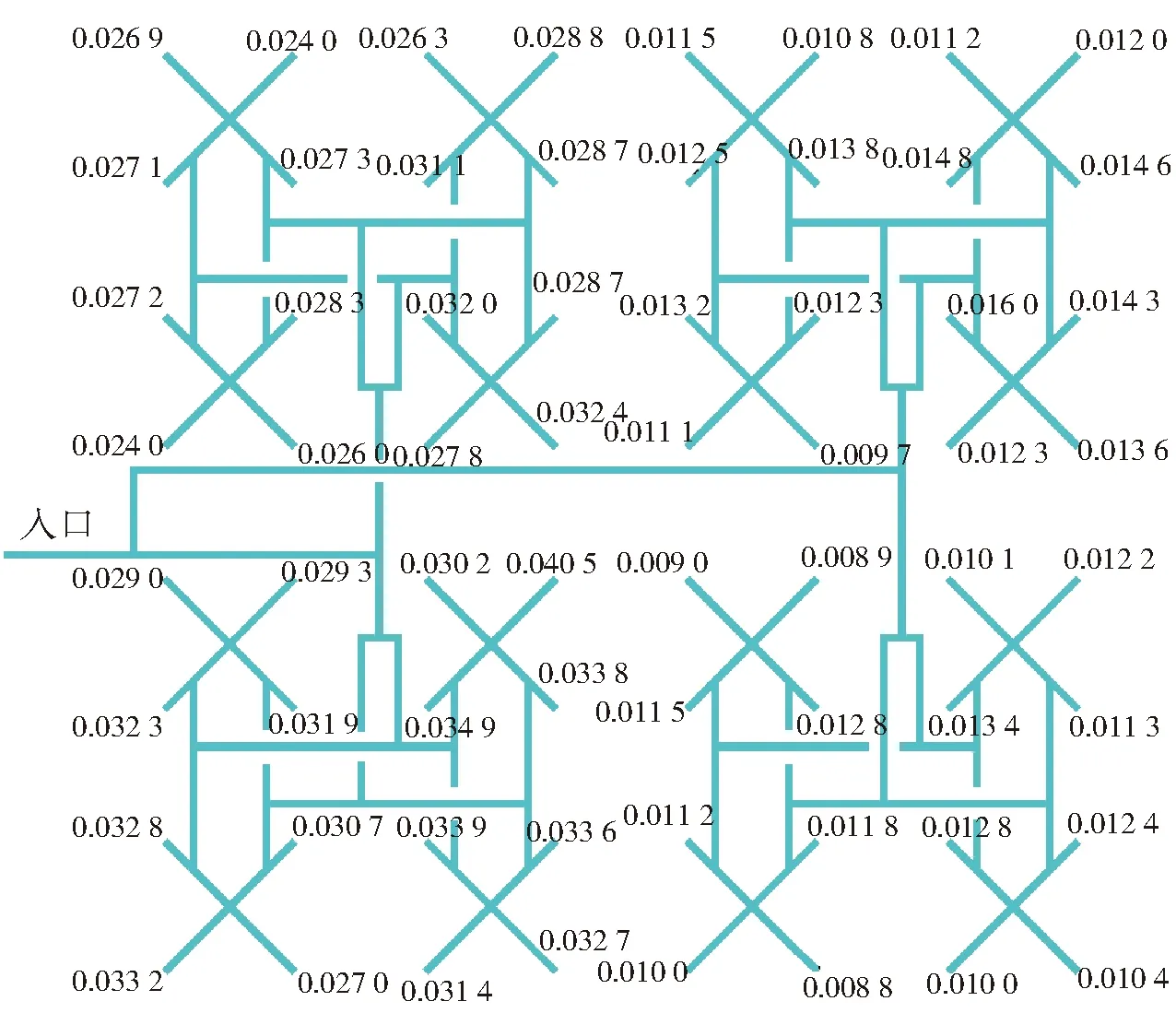
图22 方案3入口压力235 440 Pa时各出口流量(kg/s)

距进水主管较远的一级分流结构内各出口的流量较距进水主管较近的一级分流结构内各出口流量明显偏低,前者各出口流量均值为0.012 kg/s,后者为0.03 kg/s,减少约60.66%;但较远一级分流结构各出口的流量相差较小,其标准差仅为0.001 3 kg/s,而较近的一级分流结构各出口流量标准差则为0.002 1 kg/s。

由以上分析可以看出,入口压力235 440 Pa下方案3网状布水器中各出口流量分布极不均匀,前后位置流量相差很大。

改变入口压力为392 400 Pa,其他条件不变,对方案3网状布水器流场进行模拟,得到各出口流量与入口压力为235 400 Pa时的几乎一样。

图23为方案3布水器Z=0 m速度分布情况,可见距进水主管较远的一级分流结构内各出口的流量较距入流主管较近的一级分流结构内各出口流量显著降低。

图23 Z=0 m平面速度分布

由以上分析可以看出,方案3的前后两个一级分流结构的流量相差很大,改变入口压力并不能使方案3中各出口流量发生明显变化。

3 结论

对比三个方案的模拟结果可以发现,从各出口流量或单位面积流量来说,各方案都不能使流体均匀分布。方案1枝状布水器中P区域的单位面积流量高出O区域56.6%;方案2环状布水器流量相差最大的为B段和C段,当支管与环形主管夹角为30°时,C段超出B段约20.05%;方案3网状布水器中两个一级分流结构间的流量差很大,其中距入口较近的一级分流结构各出口平均流量超过较远的一级分流结构各出口平均流量约60.66%,分布极不均匀。

对比三个方案来看,方案2中各出口流量分布最为均匀,且当支管与环形主管间的夹角增大时,各出口流量进一步变得均匀。当支管与主管轴线夹角为60°时布水均匀性最好。此外,根据仿真结果可以看出,当方案2中的支管与主管轴线夹角不垂直时,由方案2出口呈一角度射出的流体会使容器内产生三维螺旋二次环流,使不同区域的流体发生混合,改善了布水器布水不均的问题。因此,方案2比其余两个方案能获得更好的实验效果。