变体飞行器伸缩翼机构设计与仿真

许 泉，周 丽，徐胜利，陆丰玮，刘思禹，刘 广，华 洲

（1.上海机电工程研究所，上海 201109；2.航天恒星科技有限公司，北京 100089；3.上海航天精密机械研究所，上海 201109）

0 引 言

传统的固定外形飞行器难以满足日益复杂的飞行环境和多任务目标要求，因此变外形飞行器的理念应运而生，并成为智能飞行器重要发展方向之一［1-3］。翼面作为飞行器重要的气动升力装置，其变形设计是变外形飞行器的研究热点。

常用的变形翼有变后掠翼、截面变形伸缩翼等，大都通过控制翼面缩展、改变翼面展弦比或采用变翼截面形状等手段，调整飞行器升阻比，优化气动焦心与飞行器质心相对位置，以获得最佳的气动性能［3-5］。

小型、低能耗、敏捷的变形机构是变形翼设计的关键，国内外研究机构和学者对此进行了大量探索。NASA兰利研究中心［6］联合美国国防高级研究计划局（DARPA）和空军研究实验室（AFRL）开展“变体飞行器结构（morphing aircraft structure）”研究，研究的大尺度变形结构可使变体飞行器适应不同飞行任务。波音公司在变外形项目中采用形状记忆合金（shape memory alloys，SMA）作为变形翼的变形驱动结构，但其变形较小、负载和响应能力低，难以满足高负载、快响应的要求，且能源消耗大。洛克希德·马丁公司［7］提出并设计了折叠翼的变形机翼，用于单一无人机实现巡航、侦察和攻击等不同飞行任务，其采用的压电智能驱动器和柔性蒙皮等结构复杂。雷神公司将现有“战斧”巡航导弹的传统弹翼改装为翼展可根据飞行条件受控变化的“伸缩翼”，增加了航程，但其空间利用率较低。NextGen 公司［8］提出了滑动蒙皮变形机翼的方案，实现变体飞行器不同飞行任务下性能的优化，但其柔性承载蒙皮成为设计难点。欧洲代尔夫特理工大学［7］基于SMA 研制了PBP（post-buckled precompressed）驱动器，实现了翼面小角度偏转，但其响应速度较慢［5-19］。国内外学者采用燃气发生器作为驱动机构，实现了亚、跨声速的巡航导弹大展弦比钻石背的设计和应用，但该机构难以实现多次缩展。国内外变形翼大都应用于低速、体积较大飞行器或原理样机，其缩展机构普遍存在空间占用大、结构复杂、翼面厚重、响应慢、负载能力弱等实际问题，难以满足小空间、低功率、大面积、薄翼面、高速可控缩展高速紧凑型弹用伸缩翼的需求。针对以上问题，本文开展了新型高速紧凑型弹用伸缩翼优化设计。

伸缩翼迭代优化过程中，采用实物样机来验证伸缩翼机构的可行性，存在成本高、周期长、调参不便等问题，且难以模拟不同飞行条件及复杂力学环境下的伸缩翼缩展性能。近年来，基于多学科协同建模与仿真的虚拟样机技术被越来越多地应用于机电系统设计中。随着该技术的发展，工程技术人员可以在短时间内快速建立虚拟样机模型，进行高效和准确设计［19-22］。

利用机械动力学软件ADAMS 和控制仿真软件Simulink，对本文提出的高速紧凑型弹用多级可伸缩翼面机构，建立了伸缩翼变形机构控制-机电联合仿真虚拟样机模型，搭建了控制-机械数字仿真流程，开展了伸缩翼变形机构的性能仿真试验，结果验证了伸缩翼面结构的可行性。

1 联合仿真基本原理

伸缩翼控制-机械一体化联合仿真建模包含伸缩翼三维物理建模、动力学数学建模及控制数学模型建模，采用数值分析手段对建立的物理模型、动力学数学模型和控制数学模型的偏微分方程组进行耦合求解，分析优化模型参数，形成物理样机开发并对优化参数进行试验验证（如图1所示）。

图1 伸缩翼机构运动特性分析框架Fig.1 Diagram for analyzing the motion characteristics of the morphing wing

伸缩翼运动特性分析框架采用Proe 软件对伸缩翼机械系统进行三维数字建模，采用ADAMS 软件对伸缩翼进行动力建模，控制系统采用Simulink 模块实现，联合仿真在Matlab 软件中实现。

首先利用Proe 软件建立机械系统的三维模型，并将Proe 软件建立的三维模型导入ADAMS 软件中，即实现Proe 软件与ADAMS 软件之间单向数据传递；其次利用ADAMS 软件完成机械系统的动力学建模，生成adams_sub 被控制模块；然后将adams_sub 被控制模块导入Matlab／Simulink 模块中；最后在Simulink 模块中建立仿真控制系统模型，设置仿真参数，即可进行ADAMS 软件和Simulink模块之间实时双向传送数据的机电一体化联合仿真。如图2 所示。

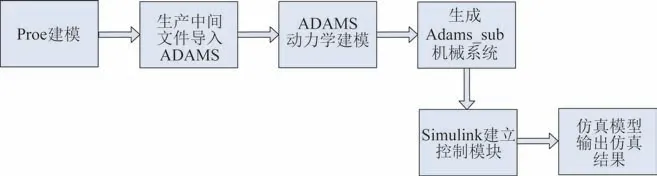
图2 控制-机械一体化建模框架Fig.2 Control-Mechanical integration modelling diagram

采用上述建立的控制-机械一体化仿真模型进行多参数分析，研究不同参数对仿真结果的影响，最终形成伸缩翼机构优化设计方案，其仿真流程如图3 所示。

图3 伸缩机构仿真流程Fig.3 Simulation process of the telescopic mechanism

2 系统建模

2.1 伸缩翼工作原理分析

伸缩翼主要包括控制器、电机、缩展机构、翼面、反馈元件5 个部分。给定期望翼面角度后，比较期望翼面角度与实际翼面偏角，产生偏差信号，经控制器处理后驱动电机转动。电机通过缩展机构驱动翼面向期望翼面角度要求的方向偏转；当实际翼面角度等于期望角度时，系统达到新的平衡状态，电机停止转动，实现角位移跟踪。系统的被控对象为翼面驱动电机，被控量为翼面角位移，输入期望翼面角位移，输出实际翼面角位移。该控制系统框架如图4 所示。

图4 伸缩翼驱动控制系统框架Fig.4 Diagram of the telescopic wing for the driving control system

2.2 伸缩翼动力学模型

变形翼由4 组翼面组成，每组翼面都由内外2 个翼面构成。驱动机构通过滑块-摆杆机构连接4 片外翼面。为实现缩展功能，驱动机构采用电机驱动丝杠传动，带动滑块驱动外翼面实现缩展动作。具体机构原理如图5所示。采用Proe软件构建头肩伸缩翼机构三维模型，将模型以x_t格式导入ADAMS/View 动力学仿真软件中，并给各个零部件指定材料属性，添加约束和载荷。翼面和传动机构均设置为刚体，并设置材料密度，定义各个运动部件之间的运动关系，设置相应的摩擦属性，单分量扭矩作为驱动属性输入变量添加在丝杠旋转副上，滚珠丝杠转动的角加速度、角速度、角位移为输出变量。

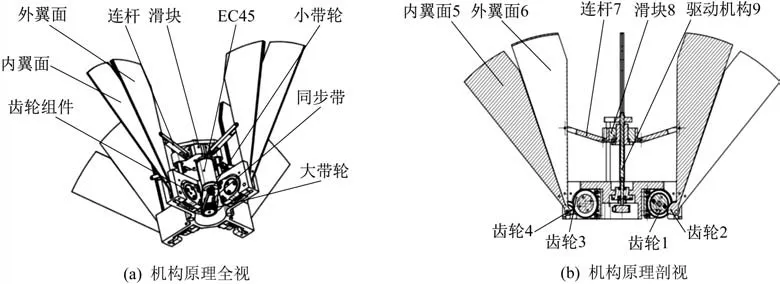
图5 伸缩机构原理示意图Fig.5 Mechanism schematic diagram of telescopic wing

伸缩翼机构动力学方程为

式中：Jr为伸缩翼绕轴的转动惯量；M1、M2分别为空气阻力矩和弹翼根部转动部位的摩擦力矩；θ为翼面转动角位移；Te为电机输出力矩。

式中：C1为阻力系数；ρ为当地气流密度；S1为导弹参考面积；L1为阻力臂；M2为摩擦力矩，包含翼面转动耳片上下结合面摩擦力矩M21、连杆铰链摩擦力矩M22及翼面转动离心力产生的摩擦力矩M23，即

翼面转动耳片上下结合面摩擦力矩为

式中：T为翼面的升力；u为摩擦系数；Rv为当量摩擦半径；n为摩擦面数。

连杆铰链摩擦力矩为

翼面转动离心力产生的摩擦力矩为

式中：M为翼面组合质量；L为翼面组合质心到翼面转轴的距离；R为轴孔半径。

弹翼展开的瞬时转动角加速度为

式中：ε为弹翼转动瞬时角加速度；φ为弹翼转动瞬时角速度。

由式（8）可得到弹翼展开瞬时角速度，二次积分可得到翼面的角位移。

2.3 伸缩翼控制系统建模

伸缩翼由电机驱动，其动子作旋转运动，无须任何中间传动机构，可直接将动作执行器作为电机的动子，实现零传动、全闭环控制。驱动电机是基于安培力设计而成的一种直接驱动电机。根据电机方程建立电压对速度的传递函数，建立闭环控制，电机方程如下：

式中：Ui为电枢的输入电压；IΩ为电枢电路的电流；RΩ为电枢电路的电阻；LΩ为电枢电路的电感；V为电枢的反电动势。

根据伺服电机的特性，可知伺服电机产生的驱动力矩与伺服电机电枢的电流成正比，因此可得：

式中：Tm为伺服电机产生的驱动力矩；Km为伺服电机驱动力矩系数。

学校发展亦或教改中都存在很多实际问题，面临种种实际困难。这些问题本身既是问题又是契机，我们必须以问题为导向，抓住学校发展的困难以及各学科独特的困难，这样才能精准发力。

伺服电机电枢的反电动势与伺服电机的转轴角速度成正比，因此可得：

式中：KV为伺服电机电枢的反电动势系数，θm为伺服电机转轴的转角。

根据牛顿第二运动定律可得：

式中：Jm为伺服电机转子的转动惯量；fm为折算到伺服电机上的有效黏滞摩擦系数；Jw为系统伪转动惯量。

在实际的系统中，通过简化方程并进行拉式变换可得到表达式如下：

由此得到带内载荷的变形翼控制系统中输入控制电压ui对应的所控制丝杠的直线运动位移hi的传递函数如下：

式中：K1为伺服器放大输入信号的倍数；i为传动结构的传送比；K0为伺服电机的传递系数；Tw为伺服电机的时间常数。

变形翼控制系统的状态方程为

3 伸缩机样机建模

在Proe软件中建立伸缩翼机构模型，如图5所示，然后导入ADAMS 软件，施加约束，建立伸缩机构虚拟样机模型，如图6 所示。在Simulink 模块中导入建立ADAMS 机械系统仿真模型，并建立位置、速度双闭环联合仿真控制模型，如图7所示。其中adams_sub为机械系统仿真模型，输出参量为螺杆的位移、速度、加速度。最外层为位置环，目标位置模块为常量模块，数值为100 rad，表示展开到预定位置。本文仿真中，伸缩机构控制策略的翼面展开速度是角位移的微分，因此，对角位移进行PID（proportional integral derivative）控制（通过前置的比例增益模块进行量纲转化）。ADAMS虚拟样机中将角位移输出作为反馈，经PID 控制，作为速度环的参考角速度；内层为速度环，参考速度为位置环输出，实际速度为虚拟样机输出的角速度反馈。

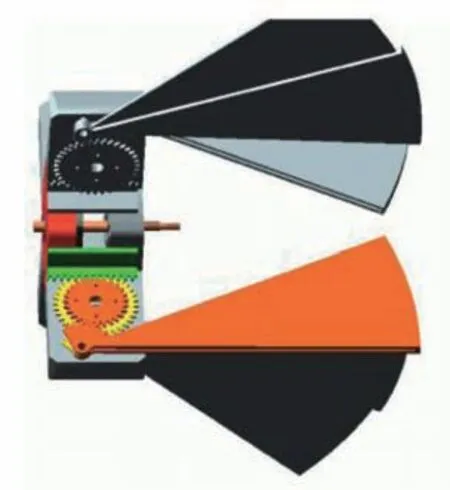
图6 ADAMS虚拟样机模型Fig.6 Virtual prototype model using ADAMS

图7 ADAMS-Simulink一体化仿真模型Fig.7 Integrated simulation model using ADAMS-Simulink

4 仿真结果分析

采用上述建立的控制-机械一体化性能仿真模型，对伸缩变形机构的动力特性进行仿真与分析，并根据工程经验选用不同材料类型的翼面进行仿真计算，如图8所示。

图8 伸缩翼展开的角位移和角速度曲线Fig.8 angular displacement and angular velocity curve of telescopic wing

根据控制-机械一体化模型，对选用不同电机控制策略和PID 参数进行仿真分析。优化后，铝合金伸缩翼为0.55 s，角位移达到25°，翼面角速度为0，伸缩翼系统达到稳定且不振荡。采用图7 控制-机械一体化模型，研究了碳纤维和铝合金两种典型翼面结构材料和不同传动比条件下，伸缩翼展开时间的影响，结果见表1。

表1 不同翼面材料和传动比仿真分析Tab.1 Simulation of different materials and transmission ratios

由表1 可见，翼面材料为铝合金的情况下，传动比为1.5∶1 时，其展开性能优于其他两种传动比；相同传动比情况下，翼面材料为碳纤维复合材料时，展开时间均优于铝合金材料。轻质材料翼面在高速展开中，对驱动电机的选型约束较小。如果将翼面展开时间控制在100 ms，铝合金及碳纤维不同材料的翼面机构，驱动力矩分别达到600 N·m 和400 N·m。

5 仿真及试验对比分析

电机选用EC-i52（6 000 r/min，18.9 N·m），翼面本体材料选用铝合金材料，传动比2∶1，进行实物测试，如图9所示。

图9 伸缩翼物理样机测试Fig.9 Result of the physical prototype of telescopic wing

本文采用自研伸缩翼缩展机构地面测试软件，对伸缩翼缩展过程进行实时动态测量。翼面展开时间为510 ms，收缩时间为520 ms。仿真模型与实物测试存在较小误差，其原因可能为翼面传动机构中多种间隙、摩擦系数、真实物理模型和仿真模型存在一定差异。实物测试结果表明，控制-机械一体化动力学仿真能较为真实地反映物理模型，因此可以作为伸缩翼结构优化分析的基础。

6 结束语

本文建立的控制-机械一体化动力学虚拟样机仿真模型，实现了变形翼缩展过程的数值仿真，得到结论如下：

1） 采用ADAMS 软件和Simulink 模块建立的控制-结构耦合仿真模型，用于变形翼机构系统参数设计，并对伸展翼展开过程的位移、速度、加速度、运动副间隙及接触过程开展研究，从设计角度提高了机构系统的运动特性和可靠性；

2） 实物试验验证了伸缩翼仿真模型的准确性，该模型可以作为伸缩翼结构优化、弹道仿真和控制系统仿真的基础。