基于等效模型的空间站大面积柔性太阳翼结构优化设计

朱春艳，孙 丹，谭金强，郑 威，胡亮亮，吴 添

（上海宇航系统工程研究所，上海 201109）

0 引 言

航天器电源系统中的太阳翼作为航天器的主要能量来源，是航天器不可或缺的组成部分。太阳翼在质量、体积和能量转换上的技术发展对提高有效载荷质量和降低航天成本非常重要［1］。NASA载人航天中心（manned spacecraft center，MSC）从20 世纪70 年代开始研制国际空间站需要的高展缩比柔性太阳翼［2-3］。航天器的能量需求，要求太阳翼具有足够的展开面积；运载火箭包络尺寸和运载能力的限制，又要求太阳翼折叠包络尺寸小且质量轻。为了满足上述需求，太阳翼的基板必须采用轻质薄板结构，目前国际上普遍采用半刚性［4-6］和柔性（基板为薄壳膜）太阳翼［7］作为主要研究对象。随着我国自主研发空间站建设的高速推进，在轨航天器对电力的需求也越来越大，目前，大面积柔性太阳翼已成功应用于我国空间站建设中［8］。

从结构特点看，大面积柔性太阳翼展开跨度大、刚度小，质量及转动惯量大，同时基板采用预应力进行张紧，因此低阶模态频率密集［9-11］。空间站太阳翼需要面临多种复杂的太空环境［12］、冲击载荷及振动条件，同时需要保证结构安全与正常发电能力，这些都是结构设计所关心的重要问题［13-15］。在保证结构功能与可靠性的基础上，减小结构质量，对航天任务的发射、空间站结构设计都有着极为重要的经济意义与工程价值。

太阳翼的设计需要考虑飞行器控制、结构系统自身的动力学问题、入轨在轨载荷环境等因素，模态分析是结构设计和动力学分析的基础。由于太阳翼结构复杂，各种零部件、机构件复杂，如何快速获取太阳翼模态分析用动力学模型，并与结构设计相互迭代，实现结构优化设计仍是一个技术难点。本文在对大面积太阳翼进行结构模态分析的基础上，基于代理模型，采用多岛遗传算法（multi-Island genetic algorithm，MIGA）全局寻优和设计非线性序列二次规划（nonlinear programming by quadratic lagrangian，NLPQL）梯度算法实现太阳翼的结构优化，探究关键结构参数对整个太阳翼结构系统的影响，为结构设计提供参考。

1 柔性太阳翼模型

本文采用的柔性太阳翼模型如图1所示。太阳翼通过驱动β 变位机构实现调姿过程，伸展臂支撑着太阳翼的在轨展开和收拢，提供太阳翼在轨的刚度和强度。在展开和受载时，上、下收藏箱支撑伸展臂；收拢时，收藏箱用来容纳折叠后的伸展臂。展开状态时通过对张紧机构施加张紧力，使基板处于张紧状态；单边电池阵通过携带的电池片实现光电能量转换。

图1 柔性太阳翼结构Fig.1 The flexible solar arrays

2 太阳翼等效模型分析

为研究各个参数对结构系统的影响，同时保证在一定精度下快速预测结构特性，将太阳翼结构等效为弹簧质量模型，该等效模型如图2 所示。其中，M1为单边电池阵质量；M3、M2分别为太阳翼上、下收藏箱质量；M4为伸展臂等效端部质量；M5、M6分别为收藏筒与变位机构质量。Ki（i=1，2，…，6）为各个质量间连接刚度。具体等效模型建立过程见文献［16］。

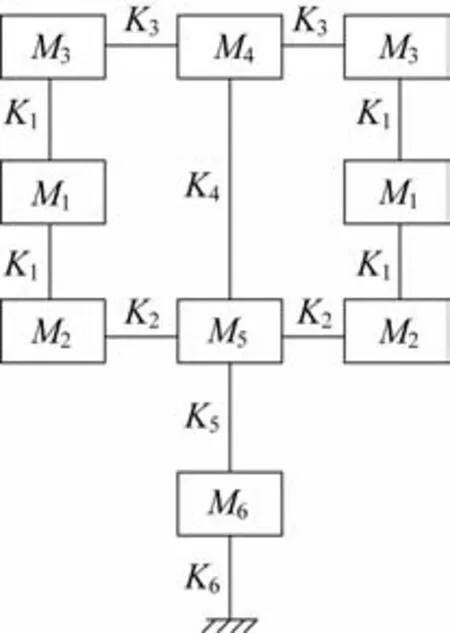
图2 太阳翼弹簧质量等效分析模型Fig.2 Equivalent spring-mass model of the solar arrays

不考虑阻尼因素，组装各个部件后得到的太阳翼等效模型为

式中：Me、Ke、X、F分别为等效代理模型的质量阵、刚度阵、位移向量及外力。

文献［10］中，将式（1）特征值分析得到的结果与采用图1 中有限元模型得到的结果进行对比，见表1。其中，等效模型分析耗时1 s，有限元模型分析耗时30 min。

表1 柔性太阳翼模型对比Tab.1 Comparison between equivalent model and FEM model

在进行侧摆分析时，未考虑单边阵平面内方向的侧摆刚度，只考虑了其质量效应，因此，分析结果小于有限元非线性预应力下模态分析结果。

3 太阳翼结构优化设计

传统的太阳翼设计基于非线性预应力的分析方法，计算规模大，流程复杂，且常面临计算收敛性问题。本文基于文献［10］中的等效模型和新建立的数值代理模型进行结构优化设计，然后在该优化设计的基础上，采用精细模型进行进一步校核和设计。优化模型为

式中：X为柔性电池翼的设计变量；f(X)为优化目标，这里为太阳翼的频率；gi(X)为设计变量总质量约束条件；a与b分别为表2 中设计变量的上、下限。

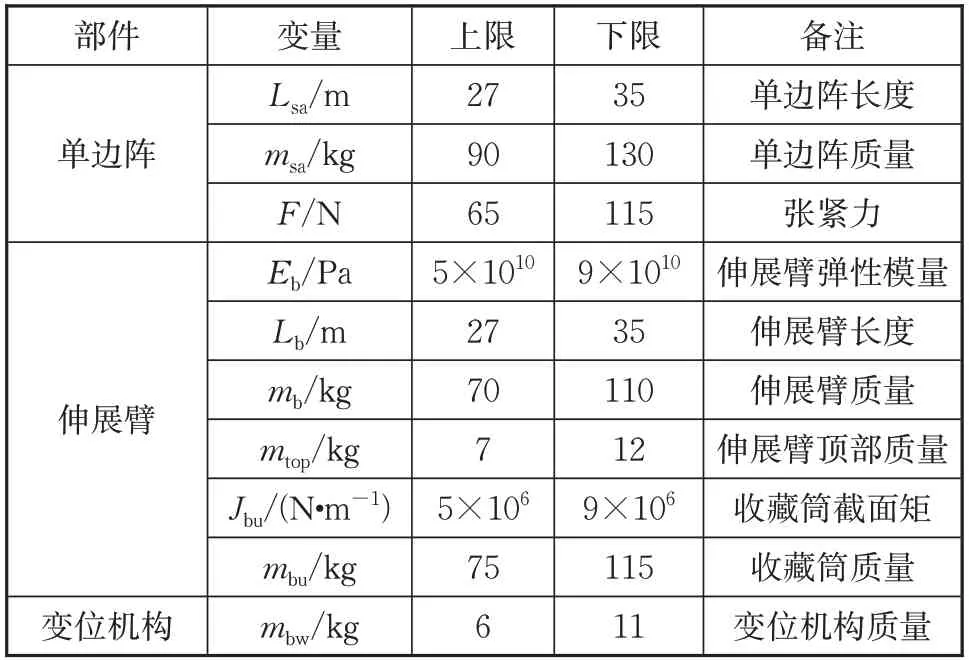
表2 设计变量与约束变量Tab.2 Design and constraint variable

本文分析模型优化目标函数f(X)具体为

式中：f1、f2、f3分别为太阳翼的一阶弯曲频率、一阶扭转频率及一阶侧摆频率。各部件名称见表2。

基于等效模型，采用试验设计法（design of experiment，DOE）开展设计，采用径向基函数（radial basis function，RBF）构造数值代理模型，以提高分析效率。分别对一阶弯曲和一阶侧摆数值代理模型展开误差分析，如图3 所示。图3 中，横坐标表示数值代理模型估算值，纵坐标表示有限元精确值，取172个采样点，采样点落在45°线上时，说明构造的代理模型精度较好。为搜索到全局最优解，采用两层优化模式，即先进行多岛遗传算法（multi-Island genetic algorithm，MIGA）全局寻优，然后在该优化结果附近采用设计非线性序列二次规划（nonlinear programming by quadratic lagrangian，NLPQL）梯度算法进行局部寻优，提高优化精度。MIGA局部寻优算法的各项参数见表3，具体优化流程如图4所示。

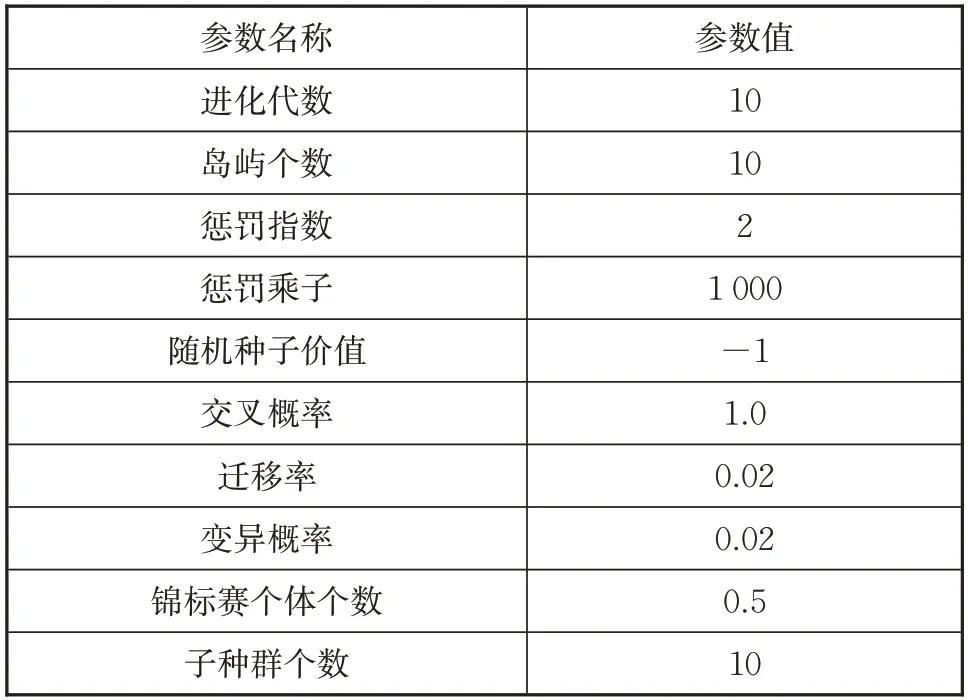
表3 MIGA算法参数Tab.3 Parameters of MIGA

图3 数值代理模型误差分析Fig.3 Error analysis of surrogate model

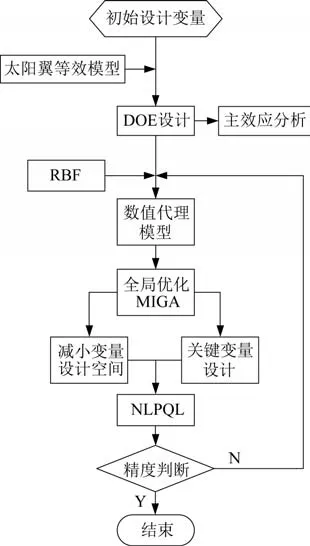
图4 太阳翼结构优化设计流程Fig.4 Structural optimization design process of solar array wing

在优化过程中考察设计变量的敏感性和主效应，设计变量主次图如图5所示。横坐标表示频率值对于某设计变量的敏感性，表现为设计变化对频率值影响所占百分比，矩形条长度越长表示这个设计变量对频率值影响越大。图5（b）和图5（c）分别对应一阶弯曲频率敏感性分析、一阶扭转频率敏感性分析和一阶侧摆频率敏感性分析。由图5 可见，对一阶弯曲频率及一阶扭转频率影响最大的是单边阵的张紧力、质量和长度，此外，伸展臂的长度和刚度对一阶弯曲频率也有较大影响。对侧摆频率影响最大的设计量是伸展臂的长度和刚度，单边阵质量、伸展臂长度对侧摆频率也有较大影响。

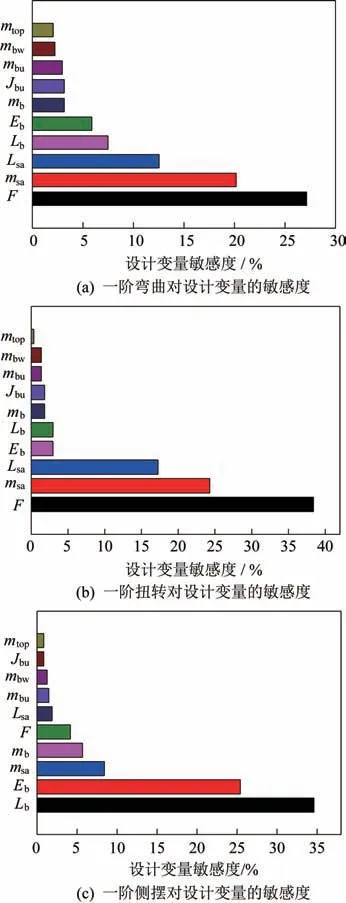
图5 设计变量主次图Fig.5 Pareto chart

设计变量的主效应分析图如图6 所示。表2 中每个设计变量的上、下限为1～2（量纲为1）之间的值，即a=1，b=2，纵轴表示单边阵一阶频率值随着设计变量的变化而变化，图6（b）和图6（c）分别为一阶弯曲频率、一阶扭转频率、一阶侧摆频率的主效应分析图。相对于图5，图6可以更加清晰地看出每个设计变量浮动量对单边阵基频的直接影响。由图6可见，提高张紧力可有效提高一阶横向、扭转基频，对一阶侧摆频率影响较小；加大伸展臂长度会明显降低一阶横向、一阶扭转基频；增大单边阵质量会明显降低三个方向的基频；提高伸展臂材料弹性模量可以提高一阶横向、一阶侧摆基频，对一阶扭转频率影响较小，其他设计变量对单边阵的直接影响也可以直观地从图中得到。

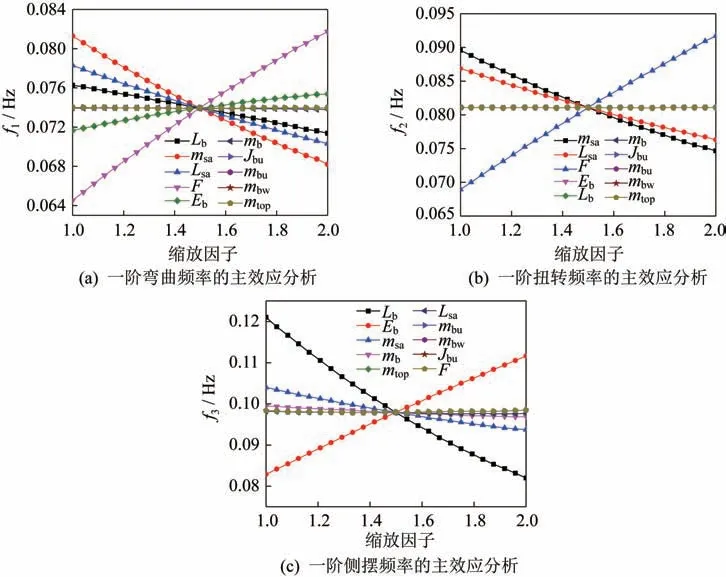
图6 主效应分析图Fig.6 Main effects plot

最终优化结果见表4。由表4可见，MIGA 优化结果与NLPQL 优化结果很接近，经NLPQL 优化后，一阶扭转频率f2为0.099 Hz，大于MIGA 优化结果0.098 Hz，f1和f3的优化结果一致性非常好。总体上看优化代理模型精度较好，使得两次优化结果接近。

表4 太阳翼结构优化设计结果Tab.4 Structural optimization design results of solar array wing

经过优化分析后，结构的一阶弯曲频率由0.069 Hz提高到0.092 Hz；一阶扭转频率由0.075 Hz 提高到0.099 Hz；一阶侧摆频率由0.091 Hz 提高到0.138 Hz。同时质量由原来的316.480 kg 减小到285.592 kg。在降低质量的同时提高了结构基频，说明两层优化的效果很明显。

4 结束语

本文基于等效代理模型，针对空间站柔性太阳翼进行快速分析，在进行DOE 设计的基础上，对影响太阳翼一阶频率的关键参数进行敏感性和主效应分析。结果表明，影响第一阶弯曲频率以及第一阶扭转频率的最大因素是张紧力，其次是单边阵质量和长度；伸展臂的长度对第一阶侧摆频率影响最大。

在DOE 设计的基础上构造代理模型，通过基于多岛遗传MIGA 全局寻优和NLPQL 梯度算法局部优化对太阳翼结构进行优化，在保证一定质量的前提下，提高优化模型的第一阶弯曲频率、第一阶扭转频率和第一阶侧摆频率。

本文方法能够高效地实现太阳翼结构优化设计，具有非常重要的工程应用价值。