高轨光学观测星座构型设计与覆盖率分析

叶 吉, 张 尧,张昆鹏, 卢少兆, 王鸿博

北京理工大学宇航学院, 北京 100081

0 引 言

20世纪90年代以来,美国大力发展各种空间态势感知系统,逐渐将天基态势感知系统作为优先发展事项.近年来先后发射MiTEx、GASSAP、ANGELS和S5等多种卫星[1-3],强化了美国对高轨目标的感知能力,并对其他高轨航天器正常工作产生影响.

与地基光学监视系统相比,天基光学监视系统工作不受天气影响[4].光学观测星座作为空间态势感知系统的一部分,主要负责目标探测与编目.因为高轨航天器数量众多、实际光学观测约束复杂,所以观测星座设计问题需要考虑庞大的设计空间和复杂的约束建模,这使得上述问题求解困难.

星座构型设计主要包括理论分析和优化设计两大类方法,理论分析侧重于建立简化假设下的数学模型,并分析最优条件.ASHLEY等[5]基于简化假设,建立了监视星座一重和二重覆盖率数学模型,并进行星座设计.RIDER[6]对多星轨道外观测(above the horizon,ATH)问题进行了数学建模,并提出一类星座部署方案.ANDREW等[7]基于计算机图像技术,对ATH问题进行数值求解.张雅声等[8]分析北半球预警星座特点后,提出一种椭圆轨道和赤道圆轨道组合的星座设计方法.后续理论研究中逐步考虑卫星的光学载荷特性,对星座参数和目标覆盖率进行仿真和设计;陈阳等[9]考虑GEO轨道探测的光学可见性约束,采用串行算法对模型进行仿真,得到了给定星座对目标的覆盖率规律.刁华飞等[10]在考虑相机指向的条件下,基于重访周期对光学监视系统进行设计.周美江等[11]基于天基太阳同步轨道,规划了两种观测模式,使星座观测不再受到地气光反射的影响.吴宇昊等[12]提出一种基于汇聚点观测的天基光学监视星座设计方法,针对GEO轨道目标分布密度较大的区间进行重点观测.优化设计侧重于借助优化算法直接设计星座构型.KATHERINW等[13-15]基于多目标遗传算法对异构卫星工作载荷、探测能力、生命周期同时进行多目标优化.陈盈果[16]使用差分进化算法进行快速响应星座设计.常辉等[17]提出卫星星座构型分层优化策略,并使用NSGA-II算法进行星座多目标优化.赵双等[18]针对失效星座的重构问题,基于NSGA-II算法采用双层编码方式对优化参数进行编码,最后得到对应的Pareto前沿,并验证结果对星座性能的提升.刘翔春等[19]针对大样本空间目标监视任务轨道设计问题,提出基于随机抽样与多变异位自适应遗传算法相结合的优化方法,从而提高优化的计算效率.

上述研究聚焦于求解目标理想分布下的最优构型,或通过数值仿真来观察光学约束下的给定构型的覆盖效果[9,20],较少同时考虑光学约束和真实空间目标分布下的星座构型设计问题.本文以GEO附近的航天器为观测目标,考虑光学约束,基于分解优化策略和差分进化(DE)算法优化求解非重复目标覆盖率最优的星座构型,并分析星座规模和覆盖率之间的关系.

1 观测卫星构型设计问题

星座构型设计问题是一个多约束、多变量的复杂混合优化问题,本节先介绍构型设计需考虑的光学可见性约束及种类,然后介绍构型设计的优化指标及计算方法,最后建立观测星座构型优化模型.

1.1 构型设计光学约束

光学观测卫星依靠目标对可见光反射实现观测,具备工作稳定、无源等优点,但会受到光学可见性约束的限制.

从约束产生原因的角度可将其为2类:(1)由航天器和天体的相对位置导致的光学可见性约束:主要包括地球遮挡约束C1、地球阴影约束C2、太阳光干扰约束C3、视场背景约束C4;(2)由光学敏感器性能导致的光学可见性约束:主要包括观测距离约束C5和观测视场约束C6.

光学可见性总约束Ct受到上述所有光学可见性约束Ck(k=1,2,…,6)影响.

Ct=C1andC2andC3andC4andC5andC6

(1)

其中,Ck为逻辑量,Ck=1代表满足对应可见性约束,Ck=0代表不满足对应可见性约束,and表示逻辑与操作.

1.2 构型设计性能指标

观测星座主要功能是对高轨的目标进行监视和编目,为后续态势感知及其他任务提供信息基础.因此,本文观测星座构型设计的目的是使星座在有限时间内对更多的非重复高轨航天器实现观测.

定义有限时间ts内,观测星座所能观测的非重复目标数与待观测目标总数之比为对应时间ts下的非重复目标覆盖率Pcover(ts),作为构型设计的优化指标J.

(2)

其中,Nobserve表示观测星座在有限时间ts内所观测的非重复目标的数量,N表示待观测目标总数.

对单个被观测航天器Tj而言,成功观测的判断方式为

(3)

其中,fj=1表示被观测航天器Tj在有限时间ts内被成功观测,fj=0则未被观测.

为了描述方便,后文将非重复目标覆盖率统一称为目标覆盖率.

1.3 构型优化问题定义

观测星座构型设计可建立为优化问题:设观测星座中的卫星数量为n,设计变量为每颗观测卫星的初始轨道根数oei0(i=1,2,…,n),在满足光学可见性约束Ct的条件下,使观测星座在有限时间ts内的目标覆盖率Pcover(ts)最大.优化模型如下:

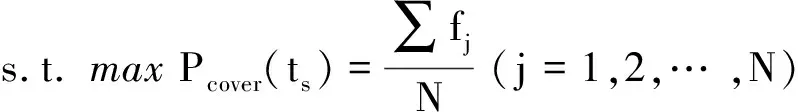
(4)

2 光学可见性约束

光学可见性约束主要包括地球遮挡、地球阴影、太阳光干扰、视场背景、观测距离和观测视场等.本节建立光学可见性约束的数学模型.

2.1 地球遮挡约束

地球遮挡指的是被观测航天器T能够反射太阳光,但反射光线在传播过程中受到地球遮挡而导致被观测航天器不可见,如图1所示.

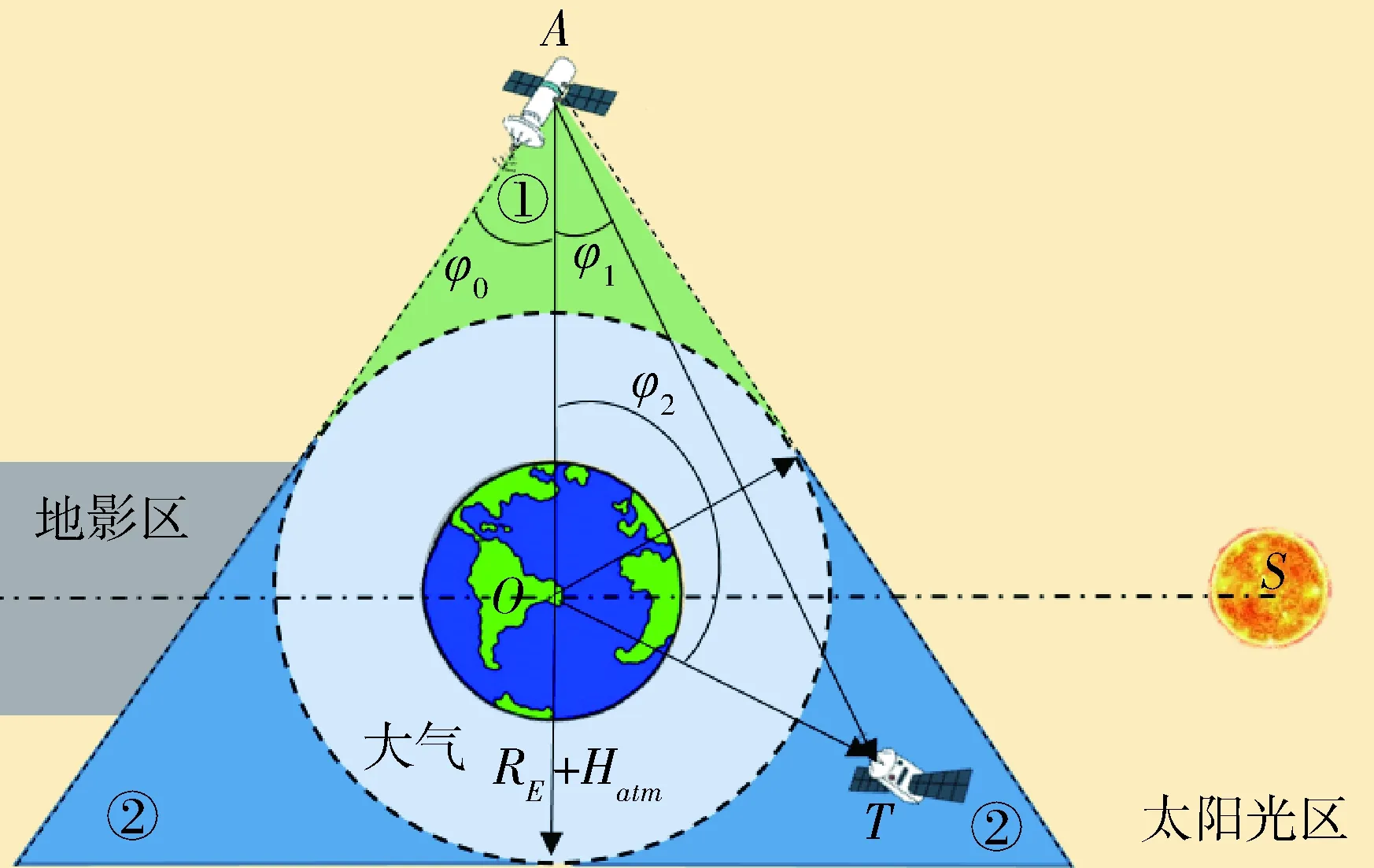
图1 地球遮挡约束示意图Fig.1 Schematic diagram of Earth occlusion constraints

地球遮挡需要考虑大气的影响,设R为遮挡体半径(R=RE+Hatm),RE为地球半径,Hatm为大气等效厚度.观测航天器A的观测视线和遮挡体将观测区域分为①区和②区,被观测航天器在①区中,观测航天器能够观测到它,但在②区中,反射的光线受到了地球及大气遮挡.因此,地球遮挡的可见性条件C1可用遮挡角φ1、φ2与等效遮挡角φ0的关系表示

(5)

其中,φ0、φ1、φ2的计算方式如下:

(6)

2.2 地球阴影约束

地影区指地球受太阳光照射,在另一侧形成的阴影区.被观测航天器T处于地影区时,无法反射太阳光,导致观测航天器A无法观测到它,如图2所示.地球阴影的可见性条件C2可用太阳夹角θ1、垂径距离hshadow和地球半径RE的关系表示

图2 地球阴影和太阳光干扰示意图Fig.2 Schematic diagram of Earth shadow and sunlight interference

(7)

其中θ1、hshadow的计算方式如下:

(8)

2.3 太阳光干扰约束

太阳光干扰指的是观测卫星A观测航天器T时,太阳作为观测的背景,强烈的亮度对光学敏感器形成严重干扰,导致无法正常成像,如图2所示.

被观测航天器T的光学可见性条件C3可用观测航天器A、被观测航天器T和太阳S的相对位置关系表示

(9)

其中,γ为逆光观测角,γob为最小逆光观测角,由光学敏感器决定.

2.4 视场背景约束

部分光学敏感器需要利用恒星背景测量目标的角度信息[19].观测航天器A轨道高于被观测对象T时,地球可能成为观测背景从而干扰对目标角度信息的测量.因为本文中星座的功能以监视编目为主,所以考虑此约束.如图3所示.

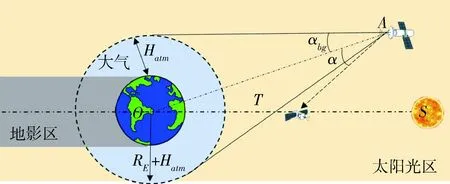
图3 视场背景约束示意图Fig.3 Schematic diagram of field of view background constraints

视场背景约束下的被观测航天器T的可见性条件C4可用观测角α和背景观测角αbg的相对关系表述

(10)

其中α、αbg的计算方式如下:

(11)

2.5 敏感器观测距离约束

观测航天器携带的光学敏感器的观测范围有限,被观测航天器T的可见距离rAT受到光学敏感器的观测极限距离Lob的限制,如图4所示.因此,被观测航天器T的观测距离的可见性条件C5为

图4 观测距离、视场范围约束示意图Fig.4 Observation distance and field of view constraints

(12)

2.6 敏感器观测视场约束

观测航天器携带的光学敏感器还受到观测视场范围限制,以固定安装的光学敏感器为例,如图4所示,当被观测航天器T和观测航天器A的连线rAT与观测视线rAM的夹角β小于光学敏感器的视场半角βob,即满足可见性条件.因此,被观测航天器T观测视场可见性约束条件C6为

(13)

3 构型优化求解

受星座规模和光学约束限制,直接求解式(4)表示的优化问题不仅计算复杂,且难以保证结果的最优性.本节用多层分支判断策略和分解优化策略对约束和优化问题进行简化.

3.1 约束处理策略

求解非重复观测目标总数Nobserve需依次计算观测航天器Ai在时间段[0,ts]内对所有被观测航天器Tj的光学可见性总约束Ct,此过程将产生巨大的计算量.

总约束Ct由所有光学可见性约束Ck共同决定,且只要存在一个光学可见性约束满足Ck=0则总约束Ct=0.因此,可将式(1)中的并集判断结构改成多层分支判断结构,且在进行条件判断时,先检验由光学敏感器性能产生的约束C5、C6可以加快总约束Ct的判断速度,如图5所示.

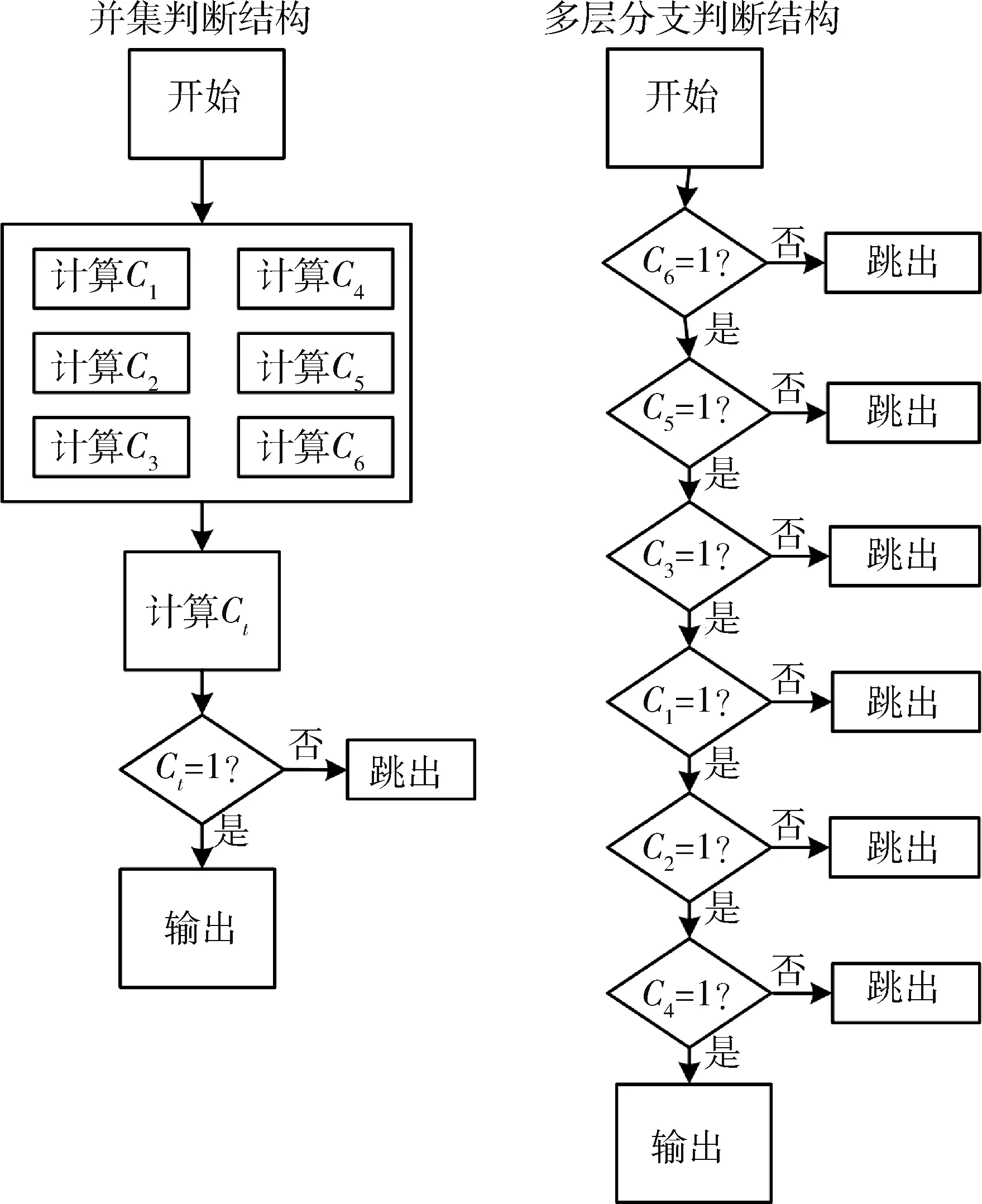
图5 多层分支判断结构处理约束Fig.5 Multi-layer branch judgment structure processing constraints

3.2 分解优化策略

观测星座中卫星数量为n,优化问题设计变量的维度为6n,当n增大时,优化问题的设计空间呈几何级增长,不仅增加求解计算量,而且难以保证构型设计的最优性.

目标监视和编目是观测星座的主要功能,本文希望合理布置观测星座构型使其能在有限时间内最大化非重复观测目标总数Nobserve,实现对更多目标的编目.

针对最大化非重复目标覆盖率的构型优化问题,本文提出一种分解优化策略,将6n维的优化问题分解为n个6维优化问题.

从整体的角度看,非重复观测总数Nobserve等于各观测航天器观测量Ni,observe之和减去星座中重复观测目标的数量N*.

(14)

要使得整个星座的非重复观测数量Nobserve最大,即要求每个观测航天器的非重复观测量Ni,u尽可能最大.分解优化的基本思路即依次优化每颗观测航天器的初始轨道根数oei0,使其非重复观测数量Ni,u取最大值.

首先,目标数据库中包含全部被观测目标,优化设计第1颗观测卫星的轨道根数oe10,使其非重复观测目标数量N1,u最大;随后更新目标数据库,移除上一颗星已观测过的目标N1,u(因为要求最大化非重复观测目标,已经观测过的目标不能重复计算),随后设计本次观测卫星的初始轨道根数oe20,使其针对更新后的目标数据库能最大化非重复观测目标数量N2,u;依次类推,直到最后一颗观测卫星初始轨道根数oen0设计完成,求解流程如图6所示.

图6 分解优化求解流程示意图Fig.6 Schematic diagram of decomposition optimization solution process

第i次优化的设计变量为第i颗观测卫星的初始轨道根数

oei0=[ai0,ei0,ii0,Ωi0,ωi0,fi0]

(15)

更新目标数据库可以避免对已观测目标的重复计算,更新的方法为在原有被观测航天器数量Ni-1的基础上,移除上一颗卫星观测的目标Ni-1,u(第1次优化时,目标数据库为初始的全部目标N).

(16)

3.3 差分进化算法

本文以差分进化算法求解上述优化问题.差分进化(differential evolution,DE)算法起源于遗传算法,但采用个体差分的方式进行变异,保留了基于种群的全局搜索策略,具备全局寻优能力强和控制参数简单、收敛快、稳定性好等优点.

DE算法主要包括种群初始化、变异、交叉、选择等步骤,本文采用DE/rand/2/bin变异策略的差分进化算法,算法的流程如下:

(1)种群初始化:设种群个体数为NP,根据优化变量下界xlb和优化变量上界xub生成种群个体

xi=xlb+rand()×(xub-xlb),i=1,2,…,NP

(17)

(2)变异:随机选择种群个体xi进行差分,得到变异个体vi

vi=xr5+F(xr1-xr2+xr3-xr4)

(18)

式中,r1～r5为1～NP范围内的随机数,且不等于变异个体的序号i,F为变异缩放因子.

(3)交叉:将x和v交叉得到种群u

(19)

式中,CR为交叉概率,D为优化变量维度.

(4)选择:根据贪婪原则选择存活的个体.

(20)

式(20)表示当ui的适应度大于xi的适应度时,选择ui作为存活个体,反之则选择xi作为存活个体.

当优化变量存在边界xlb、xub时,每代进化结束后还需要检验变量是否超出边界,对于超出边界的部分重新随机生成变量值

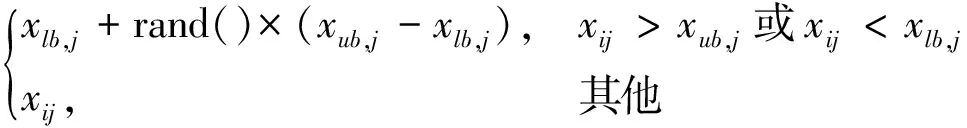
(21)

4 仿真结果与分析

目标的分布特性直接影响观测星座的构型设计,本文以真实的在轨GEO卫星为观测对象,设计观测星座构型.根据卫星数据网站(www.celestrak.com)统计GEO附近共577颗航天器轨道根数信息,结果如图7～8所示.

图7 目标半长轴、偏心率、轨道倾角的分布Fig.7 Distributions of targets’ semi major axis, eccentricity and inclination

目标半长轴、偏心率、轨道倾角都存在明显的单峰集中分布特性,这符合GEO轨道小倾角、小偏心率等特点.考虑目标偏心率和倾角均近似为0,用目标升交点赤经、近地点幅角、初始真近点角之和来描述目标在轨道上的相位.从图8可知,目标在轨道上分布并不均匀,存在多个集中分布区间.这表明在其他条件相同时,初始相位落入集中分布区域的观测卫星具备更多的可观测目标.

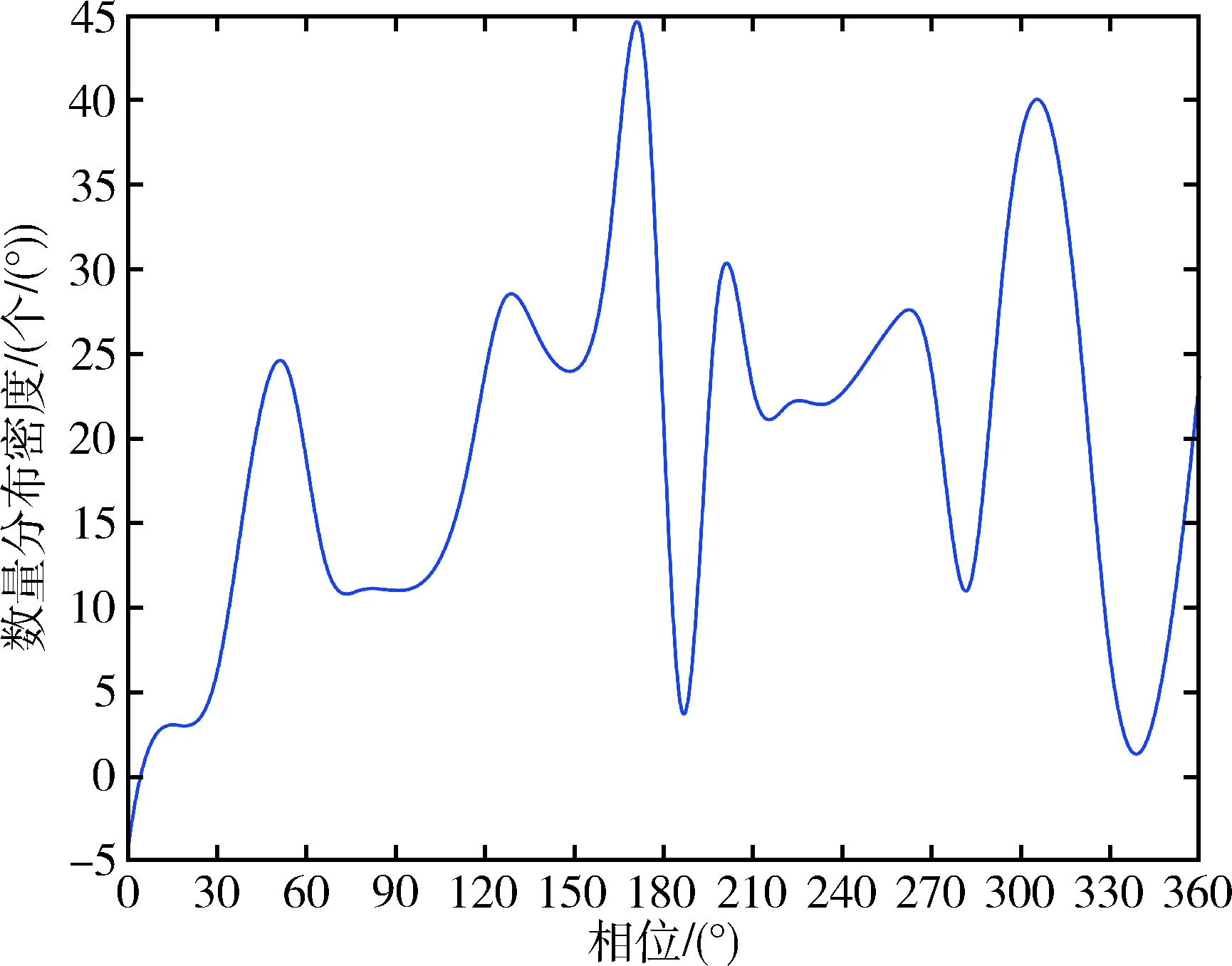
图8 目标数量随轨道相位分布的密度函数Fig.8 Density function of the distribution of target quantity with orbital phase

考虑到光学观测对卫星姿态存在一定要求,假设观测卫星具备高精度的姿态稳定能力,整个观测过程中,观测卫星的光学载荷的观测方向始终沿地心和卫星质心连线方向,并指向外部.

假设观测星座的卫星数量为6,分别使用分解优化策略和整体优化策略设计6颗观测卫星的初始轨道根数,仿真参数如表1所示,差分进化算法的参数如表2所示.观测卫星的初始轨道根数和目标覆盖率结果如表3所示.

表2 差分进化算法参数Tab.2 Differential evolution algorithm parameters

表3 观测星座卫星初始轨道根数(n=6)Tab.3 Initial orbital elements of observation constellation satellites (n=6)

从表3可知,分解优化策略对应的目标覆盖率为28.25%,整体优化策略对应的目标覆盖率为19.58%,这表明分解优化策略的构型优于整体优化的构型.

因为目标聚焦分布在GEO轨道附近,轨道相位是影响卫星观测效果的主要因素.将2种策略设计的观测卫星相位和目标相位分布进行对比,结果如图9所示.分解优化策略的相位和整体优化策略的相位都有分布在[170,180]、[190,210]、[285,330](单位(°))3个目标集中分布的区间,但整体优化策略却在[285,330]区间分布4颗卫星,可能导致重复观测而无法进一步提高目标覆盖率;分解优化策略选择将另外2颗卫星分配至其他目标区间([90,120]、[155-165] 单位:(°)),所以整体的目标覆盖率更大.

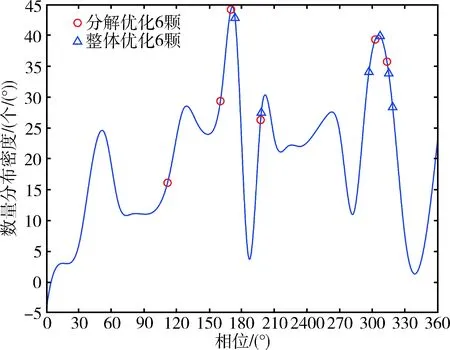
图9 整体优化和分解优化策略观测卫星相位分布Fig.9 Overall optimization and decomposition optimization strategy observation satellite phase distribution

取分解优化中与整体优化结果相近的4颗卫星(相位分别为169.82°、197.07°、302.42°、313.18°),计算目标覆盖率,结果为19.93%,和整体优化覆盖率19.58%相近,验证了上述猜想.上述现象表明整体优化可能在局部配置过多卫星,导致对目标的重复观测,进而落入局部最优.与整体优化相比,分解优化策略具备更好的全局寻优能力.

假设观测星座的卫星数量为12颗,使用分解优化策略设计12颗观测卫星的初始轨道根数,仿真参数如表1所示,差分进化算法的参数如表2所示,结果如表4所示.12颗观测卫星的相位分布如图10所示.

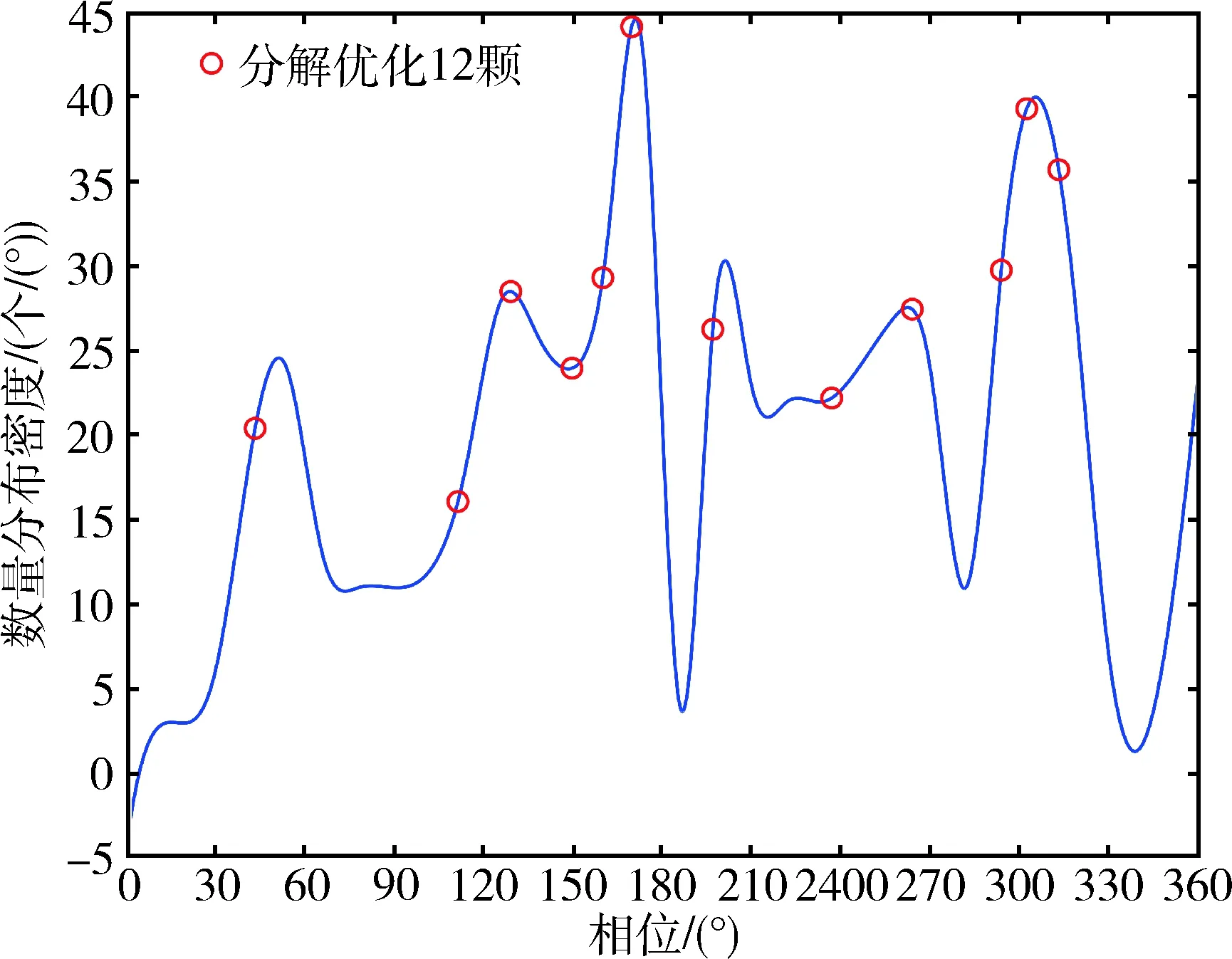
图10 星座卫星相位(n=12)Fig.10 Constellation satellite phase distribution (n=12)

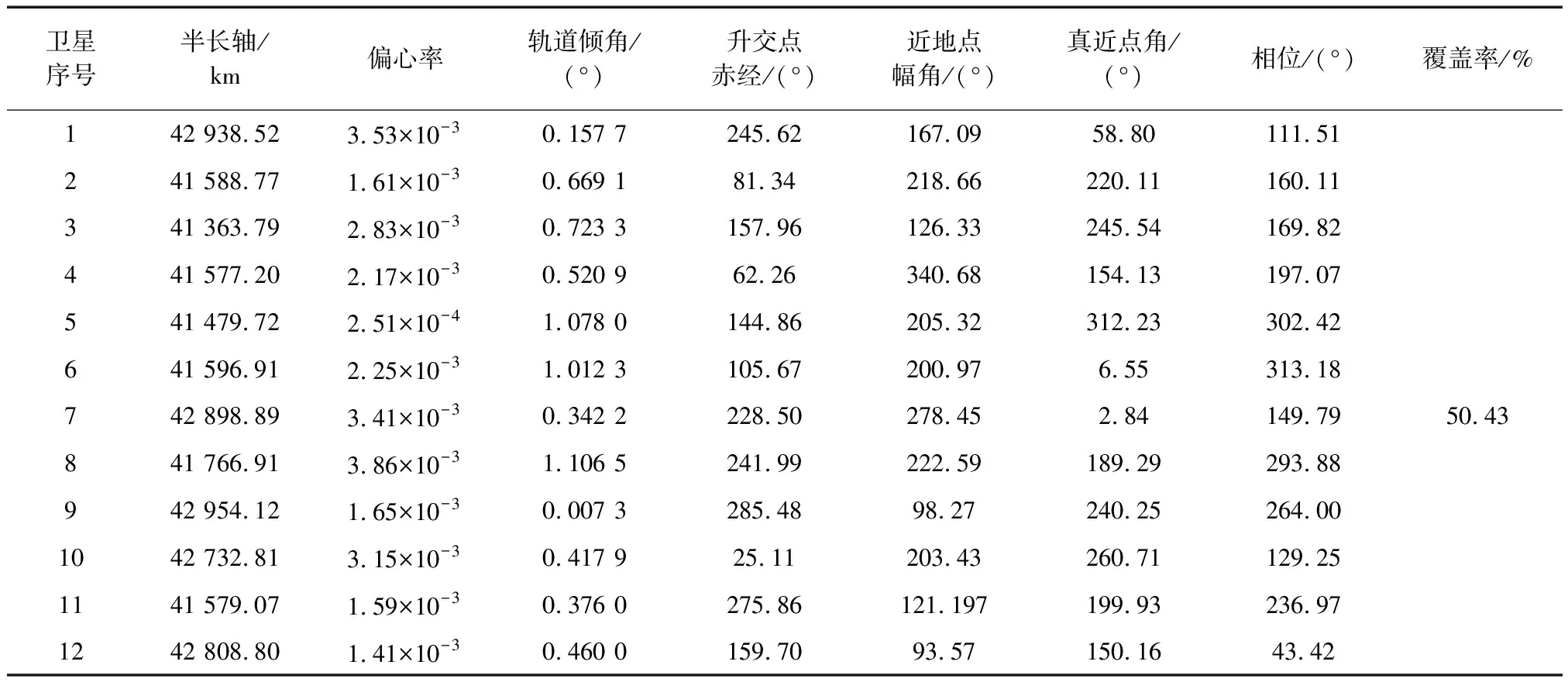
表4 观测星座卫星初始轨道根数(n=12)Tab.4 Initial orbital elements of observation constellation satellites (n=12)

在图10中,从横轴相位分布来看,分解优化策略能够使观测卫星的初始相位较为均匀地分布在目标集中的区域,从纵轴目标分布密度看,分解优化策略能依次占据目标分布密度从大到小的峰值,这些特点有助于整个星座非重复目标覆盖率最大化,这表明分解优化策略是合理的.

从表4可知,12颗观测卫星构成的星座的覆盖率为50.43%.

假设观测星座的卫星数量为30颗,使用分解策略设计30颗观测卫星的初始轨道根数,仿真参数如表1所示,差分进化算法的参数如表2所示.对比卫星数量分别为12和30的星座构型,如图11所示.记录每颗观测卫星的非重复观测数量和星座覆盖率,结果如图12所示.

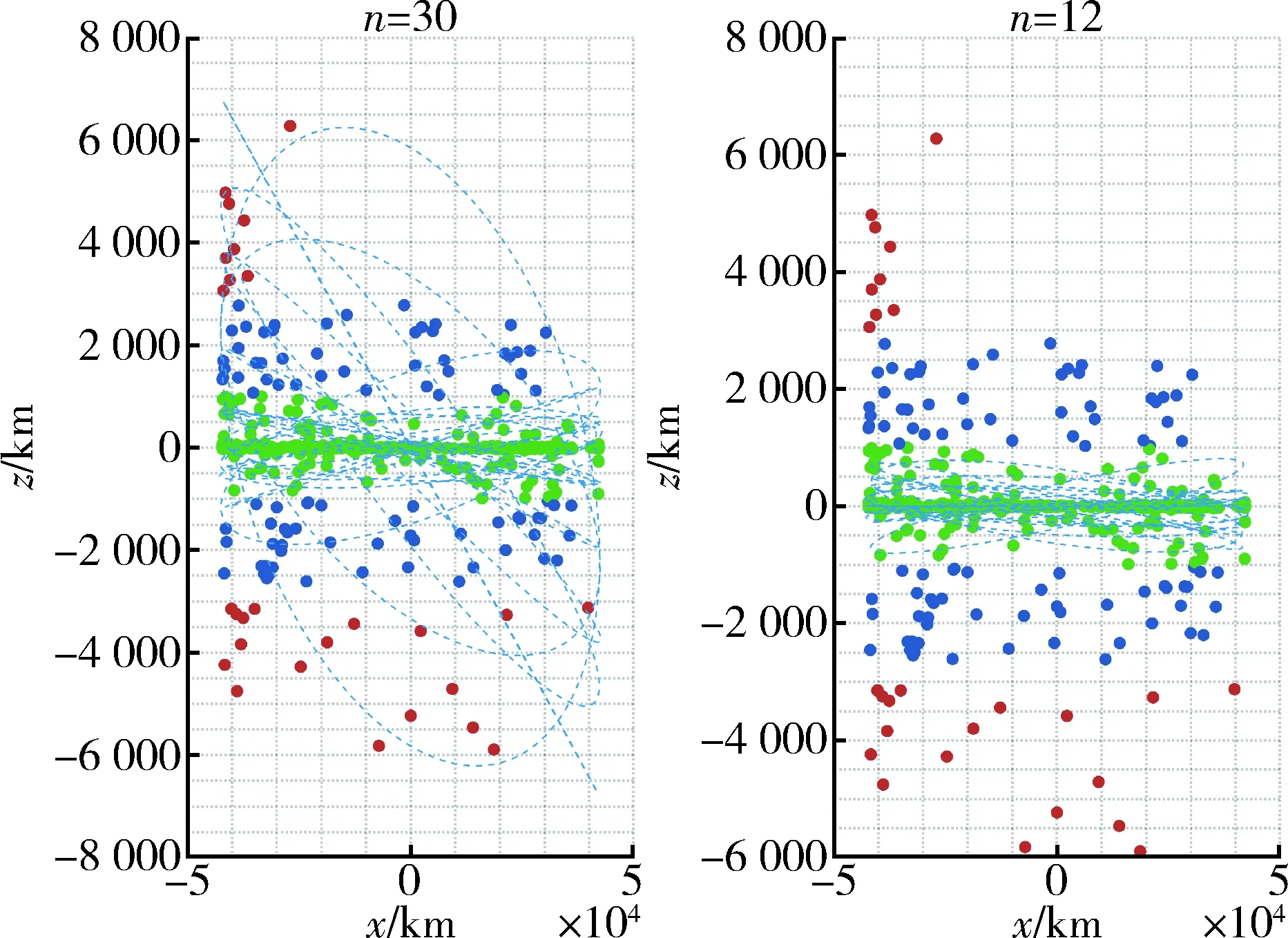
图11 不同数量星座构型对比Fig.11 Comparison of constellations with different numbers

图12 观测星座覆盖率变化曲线Fig.12 Constellation coverage change curves

从图11可知,当卫星数量增多,在z方向,星座的大致覆盖范围从1 000 km逐渐变成6 000 km,倾角的覆盖范围也从12颗的[0,1.106 5]°变成30颗的[0,9.013 1]°.这说明随着星座规模增大,星座在实现对GEO附近的大量集中目标观测后,开始试图观测离GEO轨道较远的分散目标.

从图12可知,随着星座中卫星数量的增大,每颗卫星的非重复观测数量呈现出阶梯式下降的趋势,覆盖率增长速度也逐渐放缓,这说明通过增加卫星数量而增大目标覆盖率存在边际效应,实际工程中应考虑数量和成本的平衡.

5 结 论

本文考虑真实高轨目标分布和光学约束,通过分解优化策略,将构型设计问题转换成多个单星轨道根数的设计问题,利用DE算法进行优化仿真,将分解优化策略和整体优化策略进行对比,结果表明分解优化策略具备更好的全局寻优效果,同时仿真表明观测星座规模对覆盖率增长存在边际效应.