基于Bi-LSTM网络的自由漂浮空间机械臂控制

岳博晨, 贾世元*, 王一帆, 程 潏, 陈 钢

1. 北京邮电大学自动化学院, 北京 100876 2. 北京邮电大学人工智能学院, 北京 100876

0 引 言

随着空间技术的不断探索和发展,空间机械臂在不同的在轨任务中发挥着至关重要的作用[1-2],如在轨卫星维护[3]、物体检测[4]、科学研究[5]和空间碎片清除[6]等.空间机械臂抓取未知目标以及机械臂自身模型参数的不确定性均会造成机械臂模型精度下降.模型不确定性和外部扰动因素的存在导致传统控制精度较低[7].为解决这一问题,通常通过增大反馈增益来补偿不确定性,直到达到所需的跟踪性能,但高增益控制存在诸多缺陷[8],如噪声下的大误差、执行器饱和和人机交互等应用中的安全性问题.因此,降低增益对于控制器设计是不可忽略的.

在空间机械臂控制的研究中,黄登峰等[9]利用对角递归神经网络逼近柔性空间机械臂系统的逆动力学模型,设计基于对角递归神经网络的控制方案.然而,递归神经网络存在梯度消失、梯度爆炸和长距离依赖信息能力差等问题.ZHAN等[10]提出一种基于扩展状态观测器的自适应控制器,使其能够在稳定基座的同时精确跟踪轨迹.然而,在关节控制上未考虑模型不确定性等误差.TAN等[11]为实现空间机械臂高精度、高稳定性的位置姿态控制,提出模型预测和动力学反演控制方法.然而,该方法需要较高控制增益.

为了能够更有效提升控制精度,又能降低控制增益,本文在研究中采用了双向长短期记忆神经网络(Bi-LSTM)处理模型不确定性.Bi-LSTM网络是在长短期记忆神经网络(LSTM)基础上充分利用反向序列信息,挖掘序列信息之间关系[12],在t时刻所获得的数据能同时包含过去和未来的特征信息.Bi-LSTM网络不仅保留了循环神经网络(RNN)的优势,同时也弥补了LSTM的缺陷[13-14].目前,这种网络在工业上用于诊断、预测等方面居多.王长华等[15]提出使用双向长短期记忆神经网络并结合一种基于经验模态分解的行星齿轮泵故障诊断方法.JIN等[16]提出使用双向长短期记忆神经网络将一系列新的手工特征流与原始输入信号集成,进而预测机器剩余寿命.ZHENG等[17]为有效提高旋转机械故障预测中的预测结果趋势提出一种基于Bi-LSTM的注意力机制.

针对空间机械臂的关节跟踪控制问题,本文采用Bi-LSTM网络来实现对其模型不确定性的估计.通过调整神经网络的层级、参数等条件,选择出相对较优的网络结构,改善网络的训练速度和稳态误差,并结合自适应滑模控制,达到满意的控制性能.并通过对比体现出Bi-LSTM网络的优势.此外,神经网络所得到的较高精度的模型有利于在滑模控制器选择时采用更低增益,在不牺牲系统控制精度的前提下提高系统的普适性,提升空间机械臂的运行表现.

1 问题描述与定义

考虑n自由度空间机械臂,其动力学模型方程为[18]

(1)

本文研究自由漂浮空间机械臂,且末端执行器不存在外力和外力矩,即Fb=Fe=0.此外,根据式(1)可得

(2)

(3)

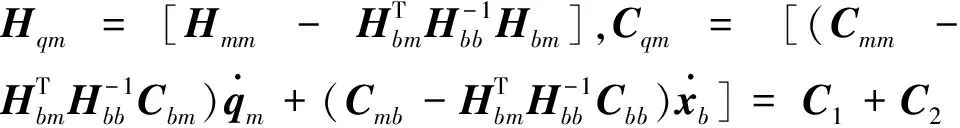
在实际情况中,很难获得精确的空间机械臂数学模型,如机械臂质量、惯量和负载质量[19].测量误差或长时间使用出现的部件磨损均导致模型不确定性产生.因此,在设计控制器时将空间机械臂模型拆分为名义模型和不确定模型,其中名义模型为已知部分,不确定模型为未知部分.广义惯性矩阵、离心力和科式力矩阵可拆分为如下形式:

(4)

其中,ΔCqm=ΔC1+ΔC2.此外,还应考虑外部扰动因素.因此,结合模型不确定性和外部扰动,自由漂浮空间机械臂动力学模型可表示为

(5)

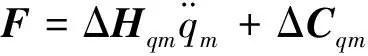
模型有如下性质和假设[20]:

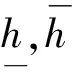
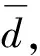
本文采用神经网络对模型不确定性进行估计.在模型估计中,假设角度、角速度、角加速度均为可测量.由于空间机械臂模型不确定性较大且具有高度非线性,因此为了能够提高网络模型估计的有效性和精度,将F中所有加法部分拆开,分块进行网络训练拟合

(6)

则有F=F1+F2+F3.

2 Bi-LSTM网络模型结构设计

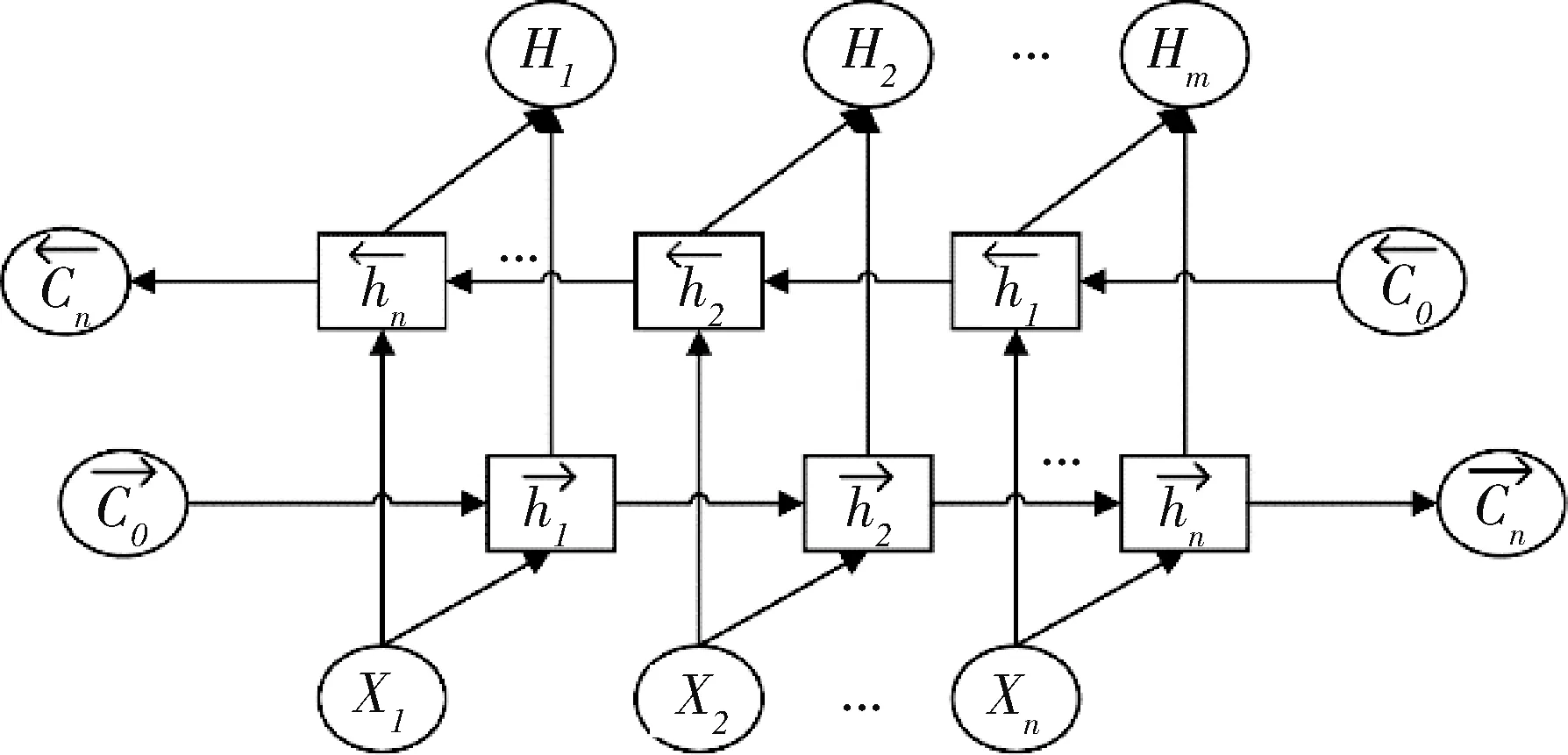
图1 Bi-LSTM神经元连接图Fig.1 Bi-LSTM neuron connection diagram

使用Bi-LSTM网络估计模型不确定性时将F分为了3部分,输入均不相同,Bi-LSTM网络结构如图2所示.

图2 Bi-LSTM网络结构Fig.2 Bi-LSTM network structure

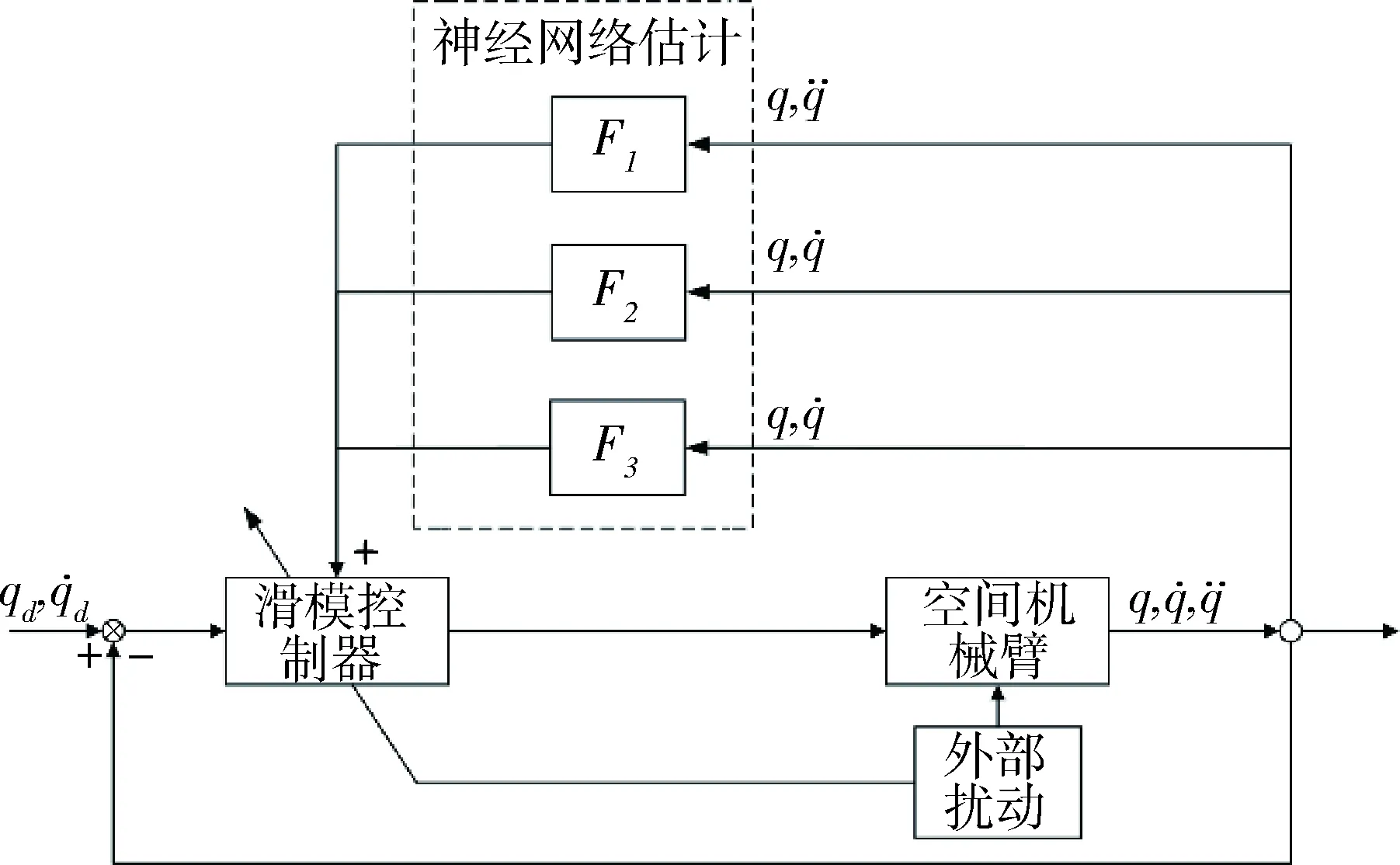
图3 控制器设计原理图Fig.3 Controller design schematic diagram

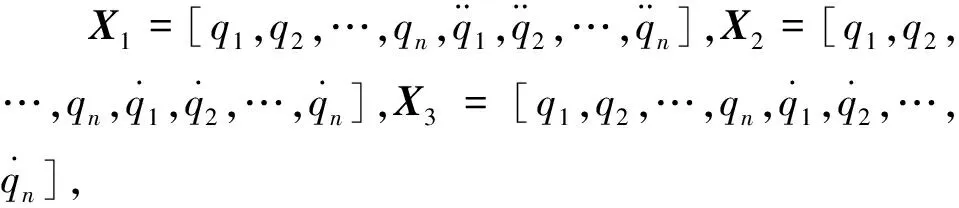
隐藏层:2层Bi-LSTM层,每层神经元个数为512.

输出层:一层全连接层.

网络设置:优化器采用“Adam”,学习律为0.001,梯度阈值为1,每次迭代使用数据量为128,数据打乱策略为每轮打乱一次,最大训练回合数为5轮,其他为默认设置.

3 控制器设计

本文主要研究空间机械臂关节轨迹跟踪问题,设计控制器原理图如下:

定义滑模面为

(7)

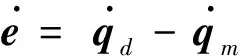
对式(7)求导得

(8)

将式(5)代入式(8)得

(9)

(10)

选用指数趋近律

(11)

根据指数趋近律设计切换控制律如下:

τs=Hqm0(εsign(s)+λs)

(12)

考虑到外部未知扰动d,设计自适应切换增益,利用自适应切换增益来消除外部扰动项.则切换控制律可写为

(13)

设计自适应律为

(14)

其中,β>0.

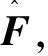
(15)

构造Lyapunov函数

(16)

对V求时间导数, 根据式(9)可得

(17)

将式(14)和式(15)代入得

(18)

根据不等式

可得

(19)

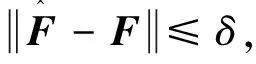
(20)

则有

(21)

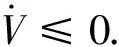
4 仿真分析

本文神经网络均使用30万组训练集进行训练拟合,考虑到训练集获取的复杂和繁琐性,本文尝试通过动力学方程和期望轨迹,自己生成训练集的方法.其中,时间采用定步长形式,训练集中动力学模型不确定性使用均匀分布随机数生成,由于负载质量范围较大,均匀分布随机数影响训练效果较为明显,因此负载也选用定步长形式生成.

为验证2种神经网络结合滑模控制器的有效性,本文以二自由度空间漂浮机械臂为例进行仿真验证,如图4所示.

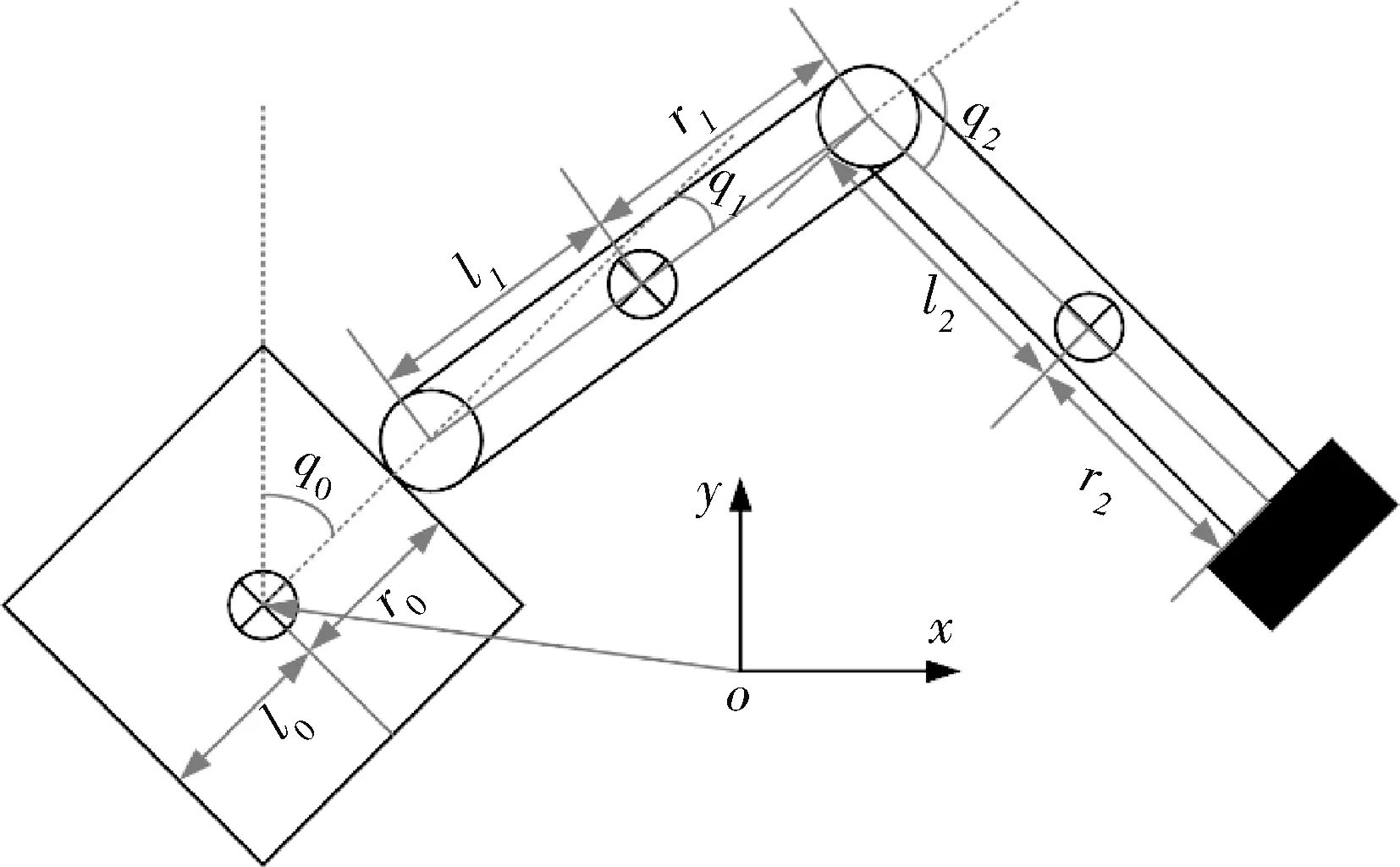
图4 二连杆自由漂浮空间机械臂Fig.4 Two-link free-floating space manipulator

滑模控制器参数选c=3,k=15,λ=15,β=45.

空间机械臂基本参数如表1所示.

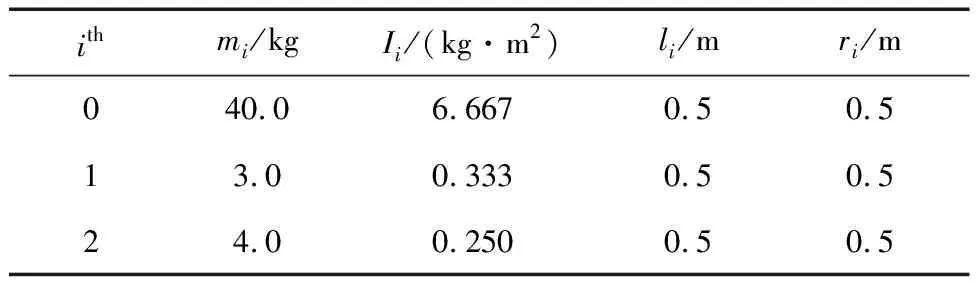
表1 空间机械臂参数Tab.1 Space manipulator parameters

mi(i=0,1,2)代表各刚体的质量,Ii代表各刚体的惯量,li和ri共同表示各刚体的长度.

本文仅考虑关节控制,则设期望轨迹

设空间机械臂初始位置与角度

即关节初始角度误差为±0.2 rad.

模型不确定性产生原因之一为末端执行器加入负载,将负载与末端执行器看作一个整体.本文使用网络训练时,设计负载范围

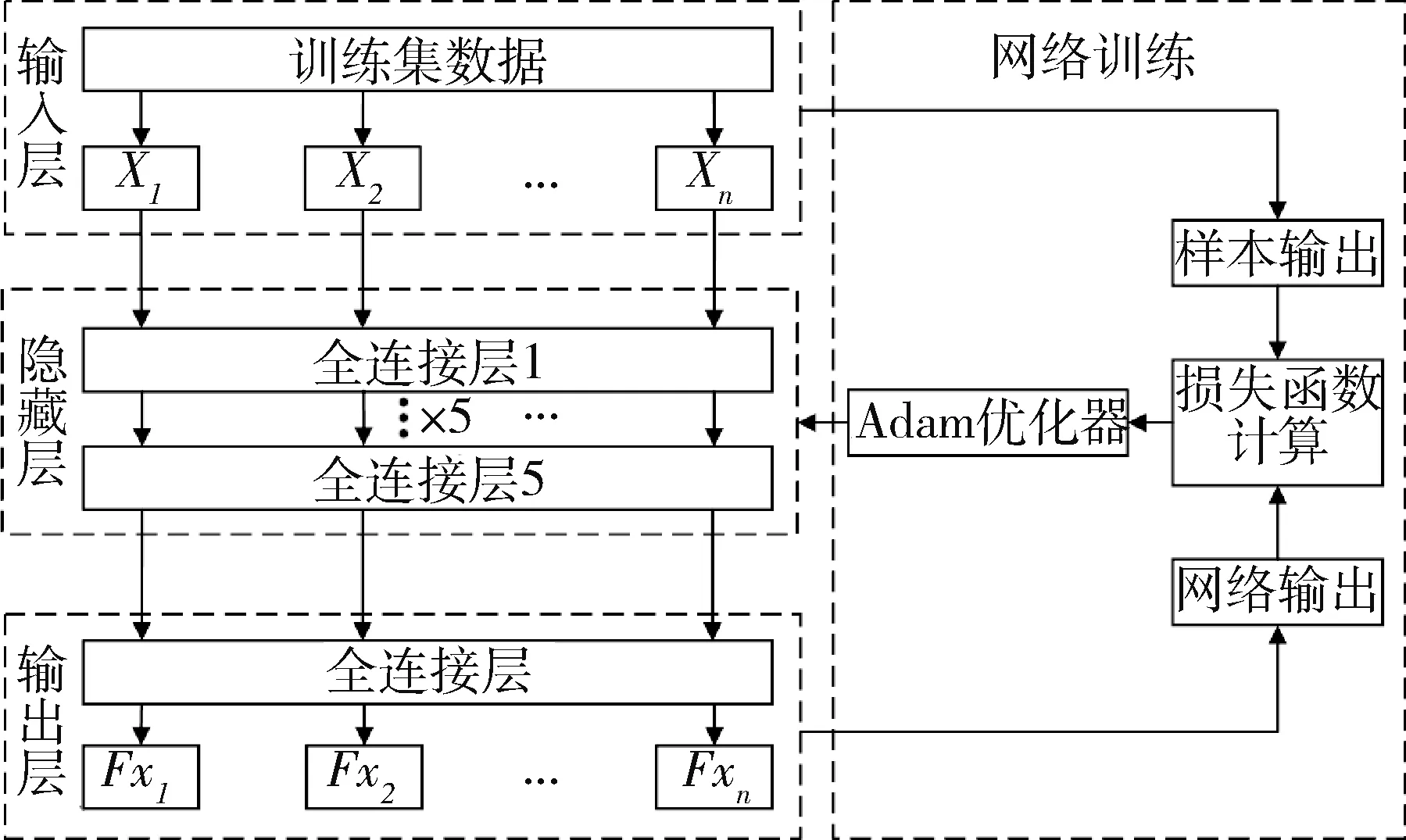
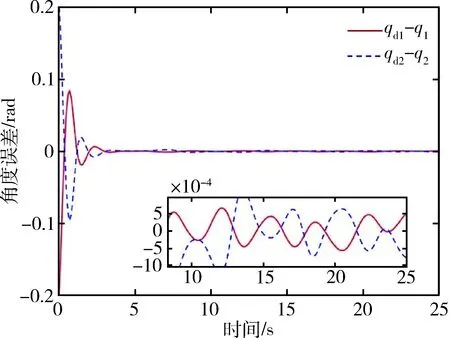
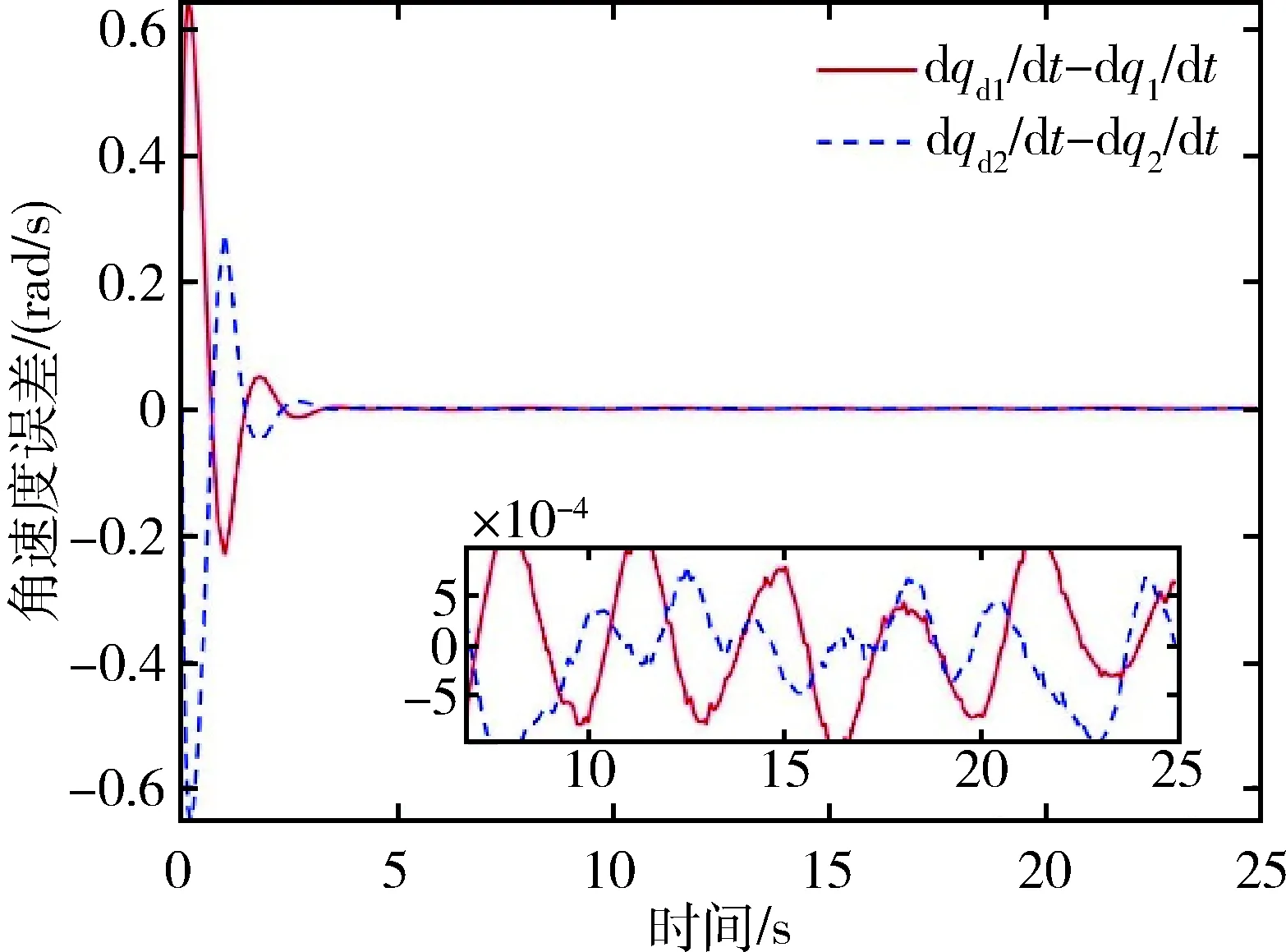
0 kg

通常情况下, 空间机械臂惯量和质量测量值与实际值会有误差, 本文考虑误差大小为

|ΔIi|≤10%Ii
|Δmi|≤10%mi

外部扰动项

为验证Bi-LSTM网络对模型不确定性的补偿效果,本文还加入了对比项,考虑到DNN网络在各领域使用非常广泛[21],且学习能力强,可以很好地筛选并拟合大批量数据[22-23].因此,采用深度神经网络DNN进行对比.DNN网络的原理和模型搭建如图5～6所示,网络输入与Bi-LSTM网络相同.

图5 DNN神经元连接图Fig.5 DNN neuron connection diagram

图6 DNN网络结构Fig.6 DNN network structure

网络设置:优化器采用“Adam”,学习律为0.000 1,梯度阈值为1,每次迭代使用数据量为128,数据打乱策略为每轮打乱一次,最大训练回合数为10轮,其他为默认设置.

本文分别对仅含自适应滑模情况和加入2种神经网络情况对两关节控制进行分析.主要研究对比加入Bi-LSTM网络对控制性能的提升情况.仿真中负载质量选用10.5 kg.

图7为自适应滑模控制下的关节角度跟踪误差响应,图8为基于Bi-LSTM网络的自适应滑模控制的关节角度跟踪误差响应,图9给出了基于DNN网络的自适应滑模控制的关节角跟踪误差响应.由图7～8可以看出,在轨迹跟踪精确性方面,未加入网络的最大误差在10-3量级,而加入网络的最大误差在10-4量级,相比之下轨迹跟踪控制的精度提升了一个数量级;从稳定性角度看,进入稳态后加入网络的波形比未加入网络的波形更平缓,更趋近于一条直线.由图7～9可以看出,基于DNN和Bi-LSTM网络补偿后控制精度较非网络补偿下的自适应滑模控制的跟踪控制精度均有提升,但Bi-LSTM网络提升的精度要高于DNN网络,尤其是第2根杆加入未知负载后,模型不确定性更大,如果臂杆数量增加,则Bi-LSTM网络体现的优势会更为明显.由此可见,Bi-LSTM网络对于模型不确定性补偿效果更为显著,对控制性能有着关键提升.

图7 自适应滑模控制的两关节角度误差Fig.7 Two joints angular errors with adaptive sliding mode control

图8 自适应滑模控制结合Bi-LSTM网络的两关节角度误差Fig.8 Two joints angular errors with adaptive sliding mode control and Bi-LSTM neural network

图9 自适应滑模控制结合DNN网络的两关节角度误差Fig.9 Two joints angular errors with adaptive sliding mode control and DNN neural network

图10为自适应滑模控制关节角速度误差,图11为自适应滑模控制结合Bi-LSTM网络的关节角速度误差,图12为自适应滑模控制结合DNN网络的关节角速度误差.可以明显地看出,在角速度方面,DNN网络对精度没有提升,而Bi-LSTM网络将最大误差大部分从10-3量级提升进入10-4量级,对于速度控制性能也有提升.

图10 自适应滑模控制的两关节角速度误差Fig.10 Two joints angular velocity errors with adaptive sliding mode control

图11 自适应滑模控制结合Bi-LSTM网络的两关节角速度误差Fig.11 Two joints angular velocity errors with adaptive sliding mode control and Bi-LSTM neural network

图12 自适应滑模控制结合DNN网络的两关节角速度误差Fig.12 Two joints angular velocity errors with adaptive sliding mode control and DNN neural network

为进一步验证算法的有效性,本文将负载重新选用15 kg进行仿真,并对角度误差进行对比,如图13～14所示,加入Bi-LSTM网络后依然可以对控制性能达到有效提升.

图13 自适应滑模控制在负载15 kg下的两关节角度误差Fig.13 Two joints angular errors with adaptive sliding mode control with a load of 15 kg

图14 自适应滑模控制结合Bi-LSTM网络在负载15 kg下的两关节角度误差Fig.14 Two joints angular errors with adaptive sliding mode control and Bi-LSTM network with a load of 15 kg

图15为加入Bi-LSTM网络的控制力矩,由图13可以看出,控制力矩初值控制在6 N·m以内,进入稳态后平稳波动且力矩不大,保证了控制力矩的合理性.

图15 自适应滑模结合Bi-LSTM网络的两关节力矩Fig.15 The torque of two joints with adaptive sliding mode control and Bi-LSTM network

图16为加入Bi-LSTM网络的基座姿态角变化图,对于自由漂浮空间机械臂,本文在控制关节运动时,基座的初始位置为0 rad,此后在±0.5 rad内摆动,即在±30°内摆动,表明机械臂在运动中未造成星本体的翻滚或失稳,保证了基座运动的合理性.

图16 自适应滑模结合Bi-LSTM网络的基座姿态角Fig.16 Base angle with adaptive sliding mode control and Bi-LSTM network

5 结 论

针对自由漂浮空间机械臂的关节跟踪控制精度问题,本文提出了通过离线学习的Bi-LSTM网络补偿模型不确定性的方式,使控制器在低增益的情况下,实现高精度控制,并与DNN网络进行对比.结果表明,网络对于模型不确定性的补偿,对控制性能提升有着显著影响,且Bi-LSTM网络的拟合性能要高于普通DNN网络,具有更好的提升效果.这使得空间机械臂控制不仅满足良好的控制性能,同时也提升了泛化能力,有效解决了空间机械臂参数的准确性问题和仅使用高增益来补偿不确定性的问题.综上所述,Bi-LSTM网络对模型的估计有利于智能控制的发展.