基于二叉树及不定长子树的集合子集求解回溯算法

赵秦怡，赵榆琴

（大理大学数学与计算机学院，云南大理 671003）

回溯算法是常用的算法设计方法，其按照深度优先的策略在搜索树中进行搜索，在搜索过程中发现当前路径不满足问题的约束条件则进行剪枝，退回上一步搜索下一条路径，以避免无效搜索，提高算法性能。回溯算法可以求得问题的所有可行解，进而根据目标函数获得最优解，适用于求解组合数较大的问题，如排列问题、组合问题、子集问题等，由于搜索树的结点数是指数阶的，故回溯算法的时间代价在最坏情况下往往是指数阶。

尚春剑等〔1〕对P-中心选址问题进行研究，在缩小问题求解规模的基础上设定搜索上界及下界，提高了回溯算法的时间性能。彭大江等〔2〕对k-CARD树问题进行研究，提出了带搜索上界和下界可求最优解的回溯算法。张学才等〔3〕提出了两种启发式的动态回溯算法求解大值域约束满足问题，利用回溯机制修正变量值，算法具有显著的优越性。胡沁等〔4〕对组合优化问题中的节点加权Steiner 树问题进行研究，提出了复杂度低且可求最优解的回溯算法。尚春剑等〔5〕研究了组合优化问题中有容量集合覆盖选址问题，提出了根据约束条件进行剪枝的高效回溯算法。

集合子集求解是常见的计算问题〔6-8〕，在很多问题求解中需要对集合子集进行枚举，如旅行商问题、关联规则挖掘、模式挖掘等。给出了基于二叉树的无剪枝子集求解回溯算法，并对常规的基于排列树的子集求解回溯算法做了改进，提出基于不定长子树子集求解回溯算法。算法极大地减少了搜索树中的结点，缩短了搜索路径，使得在搜索过程中不带约束条件、不需要剪枝，避免了常规回溯算法依据约束条件进行的大量剪枝。在问题的求解规模较大时，基于不定长子树的集合子集求解回溯算法效率更高。

1 二叉搜索树定义及基于二叉树的集合子集求解回溯算法

定义1 若将集合S 定义为

则将其子集Si定义为

1.1 二叉搜索树集合子集求解回溯算法的搜索树可采用子集树或排列树，本文提出的基于二叉树的集合子集求解回溯算法中搜索树采用了二叉树结构。其第0 层为根结点；第一层结点为子集对集合中项a1的选择情况，其第一个结点为子集中不包含项a1，第二个结点为子集中包含项a1；第二层结点为子集对集合中项a2的选择情况，第二层共有4 个结点；依此类推，第n 层为子集对集合中项an的选择情况，由于子集树中每一棵子树都是二叉树，故第n 层共有2n个叶子结点。将第一层结点的搜索子集记为S1，第二层结点的搜索子集记为S2，…，第n层结点搜索子集记为Sn，则有S1＝S2＝…＝Sn＝｛0，1｝，|S1|＝|S2|＝…＝|Sn|＝2，子集树共有2n+1-1 个结点，其中有2n个叶子结点，每个叶子结点对应一个可行解子集。

1.2 基于二叉树的集合子集求解回溯算法算法按深度优先搜索所有路径，由子集树的构造及式（2）可知，子集树中每一个叶子结点对应一个可行解子集，搜索过程没有约束条件，不需要剪枝。每搜索到一个叶子结点，生成对应的可行解子集，然后进行回溯，直到搜索完子集树中所有路径。

基于二叉树的集合子集求解回溯算法如下：

2 不定长子树搜索树定义及基于不定长子树的集合子集求解回溯算法

子集求解回溯算法的搜索树若组织为排列树，通常的求解方法中，排列树同一层中结点的搜索范围一样，第0 层为树根结点，将第一层中结点的搜索子集记为S1，第二层中结点的搜索子集记为S2，…，第n 层中结点的搜索子集记为Sn，由于搜索树中每一层结点的子树长度均相同，则有|S1|＝n，|S2|＝n-1，…，|Sn|＝1，排列树中共有n!个叶子结点，需搜索n!条路径。由式（2）可知在搜索树中只有部分叶子结点对应可行解，在搜索过程中需根据式（2）作为约束条件进行大量剪枝，以避免无效搜索，算法的时间复杂度比较高，通常为O（n!）。通常的回溯算法在搜索可行解的过程中需进行大量剪枝，算法复杂度较高，对回溯算法提出的改进策略包括相容性技术、启发式和回溯机制等。相容性技术是通过删除一些一定不在解中的变量值来缩小搜索空间；启发式是通过改变变量顺序和取值顺序来提高算法效率〔9〕；回溯机制是通过解决回溯搜索过程中遇到的矛盾来保证算法的完备性。

提出一个高效的基于不定长子树作为搜索树的集合子集求解回溯算法，算法利用相容性技术合理设置结点的搜索范围，搜索过程中无需剪枝。

2.1 不定长子树搜索树不定长子树搜索树同一层中各结点的搜索范围均不同，第0 层为树根结点，第一层第一个结点的搜索范围取集合中全n项，第一层第二个结点的搜索范围取去除a1之后剩余的n-1 项，第一层第三个结点的搜索范围取去除a1及a2之后剩余的n-2 项，第一层后续结点搜索范围依次减少，第一层最后一个结点搜索范围取最后一项。若将第一层中各结点的搜索子集记为S1.1，S1.2，…，S1.n，则有|S1.1|＝n，|S1.2|＝n-1，…，|S1.n|＝1，第二层第一个结点的搜索范围比父结点的搜索范围减少一项，后续结点搜索范围依次减少一项，有|S1.1.1|＝n-1，|S1.1.2|＝n-2，…，|S1.1.n-1|＝1，同理，有|S1.2.1|＝n-2，|S1.2.2|＝n-3，…，|S1.2.n-2|＝1，依此类推，第一层最后一个结点无下层结点，即|S1.n.1|＝0。搜索树中第一层最后一个结点为叶子结点，往下层依次类推，搜索树中每一棵子树最后一个结点均为叶子结点。n 个元素构成的集合对应的不定长子树搜索树中共有2n个结点，搜索树中每一个结点对应一个子集，不存在相同的子集，子集中均不含重复的元素。

例1 含4 个元素的集合｛a1，a2，a3，a4｝的不定长子树搜索树结构如图1 所示。

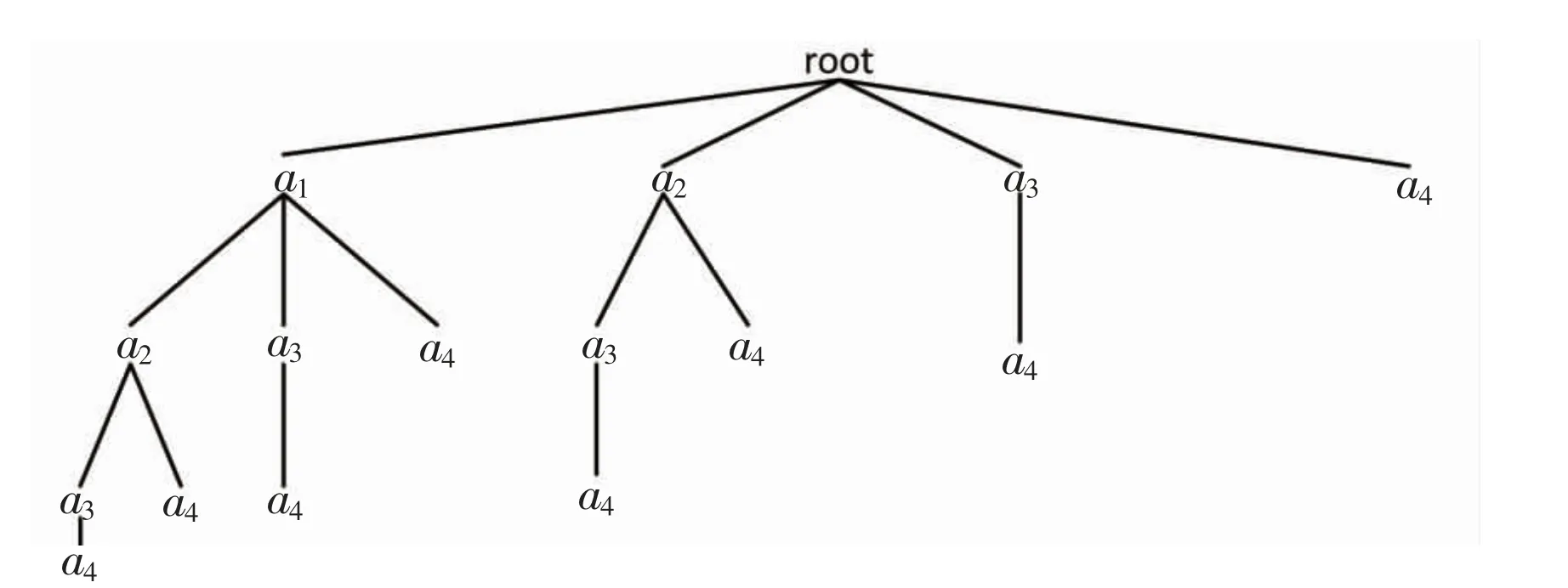
图1 集合｛a1，a2，a3，a4｝的不定长子树搜索树

2.2 基于不定长子树的集合子集求解回溯算法算法搜索过程按深度优先进行，由式（2）及不定长子树搜索树的结构可知，每搜索到一个新结点可生成一个子集，搜索到叶子结点则回溯到上一步，继续按深度优先进行搜索，直到搜索完所有结点，即得到所有的可行解子集。可行解中不存在相同的子集，子集中均不含重复的元素，且搜索过程中不需要剪枝。由以上不定长子树搜索树的结构可知，改进的不定长子树搜索树将结点数减到最少，搜索路径缩到最短，搜索过程中不带约束条件，极大地提高了搜索效率。

例2 例1 中的不定长子树搜索树按本算法进行搜索得到的子集分别为：｛a1｝，｛a1，a2｝，｛a1，a2，a3｝，｛a1，a2，a3，a4｝，｛a1，a2，a4｝，｛a1，a3｝，｛a1，a3，a4｝，｛a1，a4｝，｛a2｝，｛a2，a3｝，｛a2，a3，a4｝，｛a2，a4｝，｛a3｝，｛a3，a4｝，｛a4｝。

在回溯算法中，问题的搜索树是虚拟的，不需要在算法运行时构造一棵真正的树结构，通常的回溯算法需按某种顺序依次考察笛卡尔积S1×S2×S3×…×Sn中的元素，并根据约束条件进行剪枝。本算法中，由于采用了不定长子树作为搜索树，搜索树中子树的长度均不一致，即搜索树中所有结点的搜索范围均不一样，故在搜索过程中需合理设定每一个结点的搜索范围。当前搜索结点有两种情况：（1）按深度优先从上层结点搜索到本条路径中的下层结点；（2）从下层结点回溯到上层结点。搜索树中一个结点对应一个可行解子集，每搜索到一个新结点时生成一个子集，故需要在结点中标记搜索路径及当前搜索项。算法中搜索树结点数据描述为：

3 算法效率

通常的回溯算法搜索树中结点和搜索路径存在大量冗余，算法在最坏情况下的时间复杂度往往到O（n!），搜索过程中需要大量剪枝，算法效率低。本文中的两个回溯算法采用了相容性技术，在搜索过程中不需要剪枝，算法在最好、最坏及平均情况下时间复杂度均一样。基于二叉树的集合子集求解回溯算法需搜索树中每一个结点，搜索树共有20+21+22+23+…+2n＝2n+1-1 个结点，其中叶子结点对应可行解，算法时间复杂度为O（2n+1），n 为集合的长度。基于不定长子树的集合子集求解回溯算法也需搜索树中每一个结点，每一结点对应一个可行解子集，树中共有2n个结点，算法时间复杂度为O（2n），n为集合的长度。

当n 值较小的时候，由算法时间复杂度可知两个算法效率区别不明显，当n 值较大时，两个算法效率差别较大。表1 是两个算法在不同集合长度下的运行时间，图2 是两个算法运行时间的差值在不同集合长度下的变化趋势。当n 值较小时，两个算法运行时间及变化趋势区别不明显，算法效率相当。当n 值较大，即集合长度超过14 项时，基于不定长子树的集合子集求解回溯算法运行时间变化趋势缓慢，时间效率较好，算法更为有效。

表1 两个算法在不同集合长度下的运行时间

图2 两个算法运行时间差值变化趋势

4 结语

回溯算法设计技术适用于求解组合数较大的问题，提出基于二叉树及不定长子树作为问题搜索树的集合子集求解回溯算法，算法可求解所有的可行解子集，由于算法设计采用了相容性技术，在深度优先搜索过程中不需要按子集约束条件进行剪枝，两个算法的时间复杂度均比一般的回溯算法理想。算法时间复杂度及算法运行效率表明，问题求解规模（集合长度）较大时，基于不定长子树的集合子集求解回溯算法的时间效率明显高于基于二叉树的集合子集求解回溯算法。