MV-Raft：一种新的基于多维向量的联盟链共识算法

伍桂锋，胡 伐，曾 新，杨邓奇，李晓伟

（大理大学数学与计算机学院，云南大理 671003）

区块链技术是密码学、分布式系统和存储系统的综合应用，具有不可篡改、表示价值所需的唯一性、智能合约和去中心自组织这四大特性，其可以广泛应用于各种分布式账本系统〔1-2〕。区块链根据开放对象的不同可以分为公有链、私有链和联盟链。联盟链因具有一定的准入机制，进一步提高了应用的可信度，是区块链3.0 的一个重要方向〔3〕。

共识算法是区块链要解决的关键问题。根据区块链性质的不同，区块链的共识算法也有所区别〔4〕。存在恶意节点的环境中共识算法一般采用拜占庭容错（Byzantine fault tolerance，BFT）算法，如实用拜占庭容错（practice Byzantine fault tolerance，PBFT）算法〔5〕及HotStuff 算法〔6〕，这两种算法可以在恶意节点的攻击下达成正确的共识。同时在这种场景下多位学者也提出了改进的策略〔7-9〕。在节点可信的环境中一般采用非拜占庭容错也称作崩溃容错（crash fault tolerance，CFT）算法，具有代表性的算法有Paxos〔10〕、Raft〔11〕。由于Raft 算法简明高效，已成为联盟链中默认的共识算法。本文详细分析Raft 相关算法，总结出已有Raft 改进算法的优缺点。

K-Raft（Kademlia-Raft）算法由Wang 等〔12〕设计，通过在分布式网络中加入Kademlia 的P2P 层，检查网络节点之间的ping 值，通过异或运算建立一种分布式哈希表保存节点信息使内部形成一个完整拓扑结构。该算法每个节点的内部保存一个红黑树结构的K-Bucket，在选举的过程中，节点优先从K-Bucket 中进行选举活动，在未获取到超过半数的节点投票情况下才会再进行全局选举。这样会减少节点状态的切换，从而使分布式网络选举过程得到稳定。B-Raft（Byzantine fault-tolerant Raft）算法由Tian 等〔13〕设计，算法运用Schnorr 进行数字签名（一种椭圆曲线的非对称加密算法），在每个节点初始的时候加入证书。在选举的过程中，节点收到选举信号后，对信息进行验证。如果验证通过则进行相应的投票，以此保证信息没有被篡改，保证符合BFT 节点能当选。LC-Raft（log calculation Raft）算法由马博韬等〔14〕设计，算法通过节点内部计算历史日志记录的方式，将各节点的日志中对心跳信号的反应情况保存在最近的时间节点内，如节点报错、节点当选以及日志异常等情况。对上述这些情况，算法通过打分机制来定义节点的稳定性。

上述工作大都只考虑了影响Raft 算法的网络因素，然而实际Raft 算法还应考虑节点自身的影响因素。本文考虑在节点多维度影响因素下研究Raft算法，提出一种新的基于多维向量的联盟链共识算法——MV-Raft（multidimensional vector Raft）。算法在某些特定场景下采用设定多维特征值向量的方式，解决共识达成的速度问题以及日志同步问题，提高Raft 算法的效率。

1 背景知识

1.1 Raft 的概念Raft 算法是由Ongaro 和Ousterhout于2014 年在Raft：In Search of an Understandable Consensus Algorithm 论文中提出的，其是在Paxos 算法的基础上结合实际工程的改进。Paxos 算法由Lamport 于1998 年在The Part-Time Parliament 论文中首次公开，在实际的工程中应用于国内外多个系统中。但是Paxos 算法晦涩难懂，工程实现上也有难度，所以在Paxos 算法的基础上开发出了Raft 算法。在近些年的工程应用以及研究中，Raft 算法成为很多分布式系统的基础〔15-18〕，如开源系统Etcd、Consul 及Google Omega 调度架构，国内阿里巴巴的DLedger 等。在区块链中，联盟链HyperLedger Fabric的默认共识算法机制就是Raft。

Raft 算法易于理解和实现，其原理如下：在一个网络域中存在着多个节点，它们可能存在3 种状态，跟随者（follower）、领导者（leader）和候选者（candidate）。跟随者节点会定时向领导者节点发送心跳信息，一旦跟随者发现接收不到领导者节点的心跳返回信息，它就会将状态机转为候选者节点。在成为候选者状态时，节点内部会激活选举随机定时器。通常这个定时器的时间范围在［150，300］，在这个随机时间之后，候选者节点会发送选举信号广播给其他节点（信号中包含了它的版本号和任期）进行拉取选票。节点状态机的转换过程见图1。

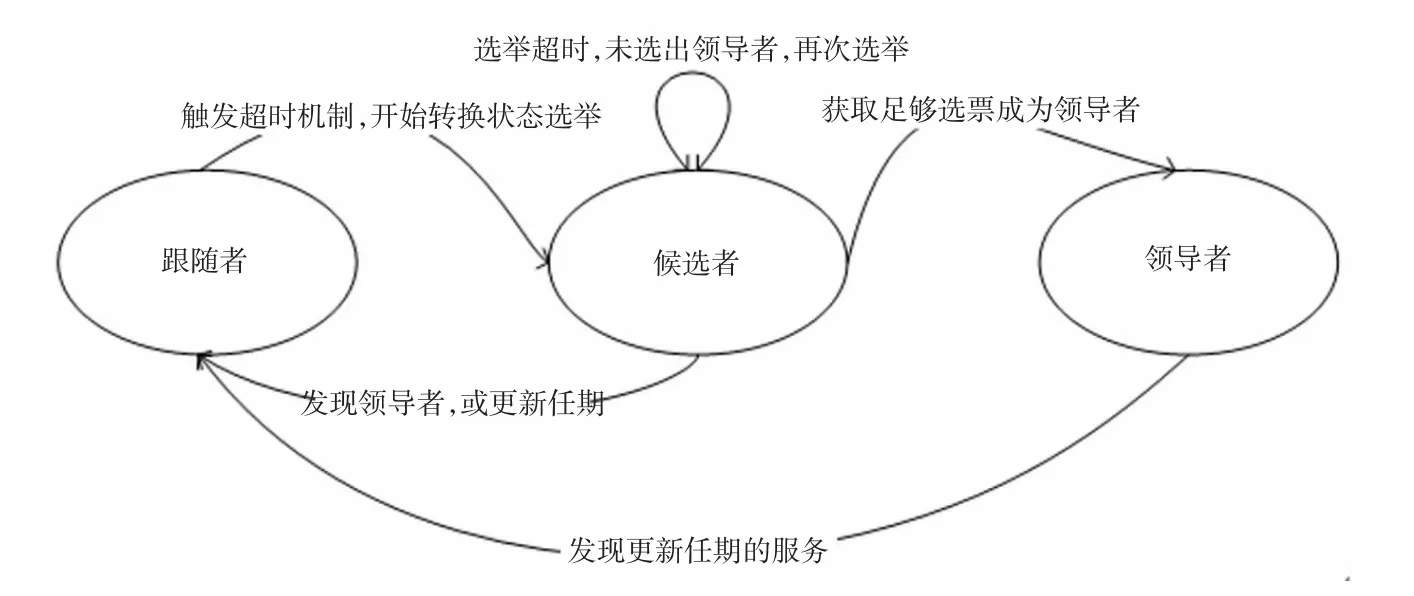
图1 Raft 选举状态机的转换

在以上过程中，得到满足条件票数（通常是超过半数的选票，以免使系统产生脑裂即多个领导者）的候选者当选为领导者节点。当选的领导者节点会向所有节点发送当选的信号从而结束竞选过程，之后由领导者节点发起日志复制过程。由于不同时期的日志不同，所以日志需要分块，系统中称之为日志条目。这些日志根据不同的任期进行压缩分块以及快照，跟随者节点向领导者节点发送心跳信号的时候会校验这些日志，并由此同步更新当前任期日志条目。完整的Raft 流程见图2。

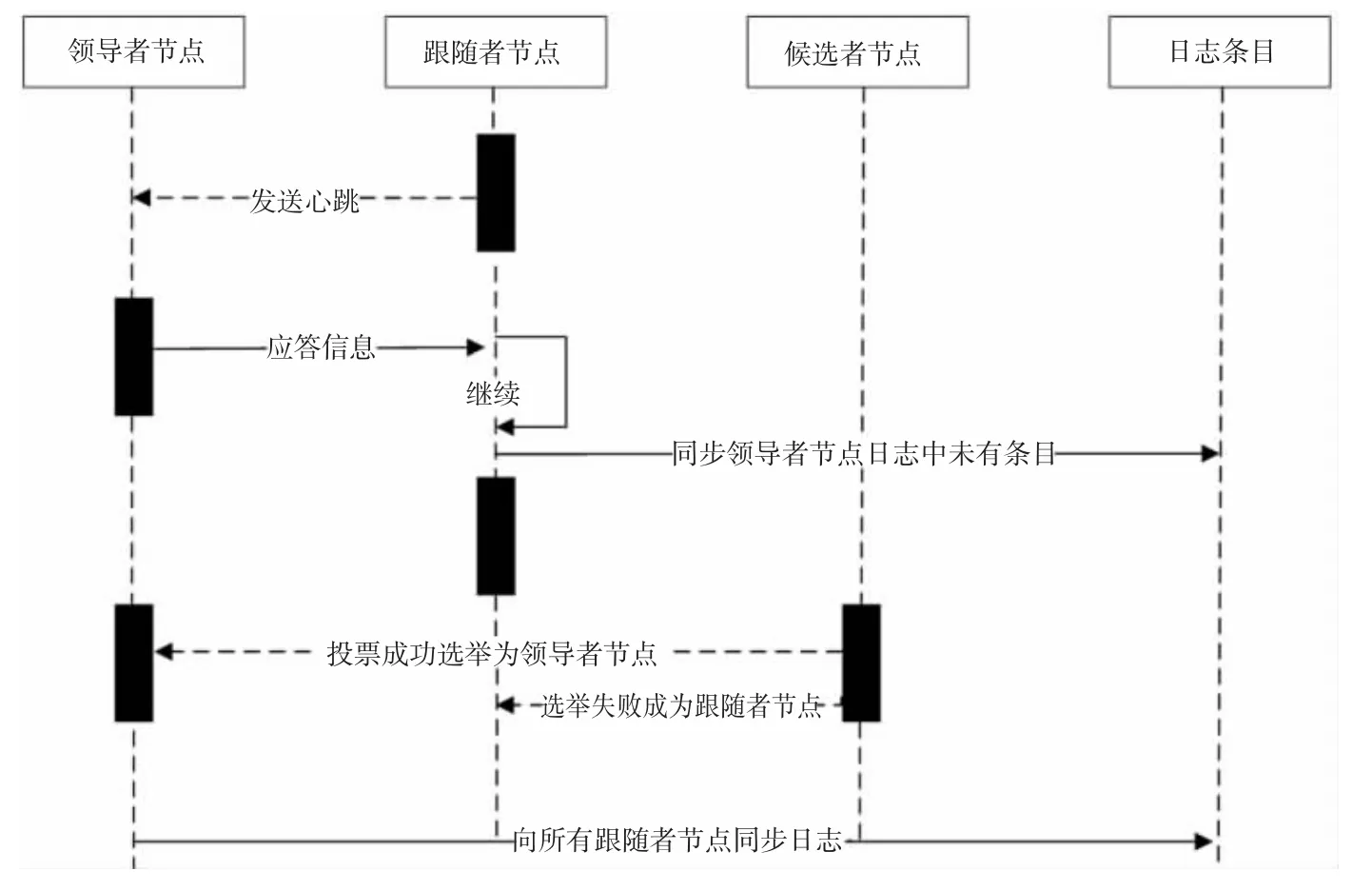
图2 Raft 运行流程

综上，Raft 算法是分布式基础理论BASE 理论的一种最佳实践，即算法同步了所有节点的信息满足了最终一致性（eventually consistent）；在状态转换过程中满足了软状态的特性（soft state）；领导者节点崩溃也可快速恢复从而满足了基本可用（basically available）。

1.2 多维向量的概念与应用多维向量是一种数学上的概念，将不同维度的统计数据组成多维向量，而多维向量是在多维空间的点。其在现实中的意义可以描述事物在多维空间中的关系，有很广泛的用途。在多维空间中两个多维向量间的距离可以表达出事物的关联度。在机器学习中K-Means 算法利用的是多维向量的欧氏距离的原理，对抽象节点进行聚类。相邻近节点间的共性一定更多，所以邻近节点间交互更加便利。

根据上述思想可以推断出：在分布式网络中，如果不同的节点之间由多维向量所计算的欧氏距离较小，则它们之间相似度较高。相似节点间进行操作消耗的各类资源会比欧氏距离大的节点间操作所消耗的资源少。在大量的实践中，人们发现只要提取的特征值是正确的，那么欧氏距离较小的节点之间的相似度较高，从而容易归类让节点间操作更节省资源。

2 算法设计与分析

本节基于多维向量特征值提出MV-Raft 算法并从多维向量的处理过程、节点选举优化、日志复制优化和新节点的处理这4 个方面来详细描述，最后分析整个算法过程中对分布式系统的影响。算法中节点在初始化或新加入分布式系统时提取特征值和做初始化计算。过程如下：首先依据影响因素选取m 个特征值组成特征值向量，将其放入节点所在局域网，将上述特征值向量广播全网络，每个节点计算出欧氏距离并保存欧氏距离最小的节点放入缓存数组以便选举和同步时使用。在节点内部放入定时器重复上述流程，对新加入节点也重复上述过程。流程见图3。

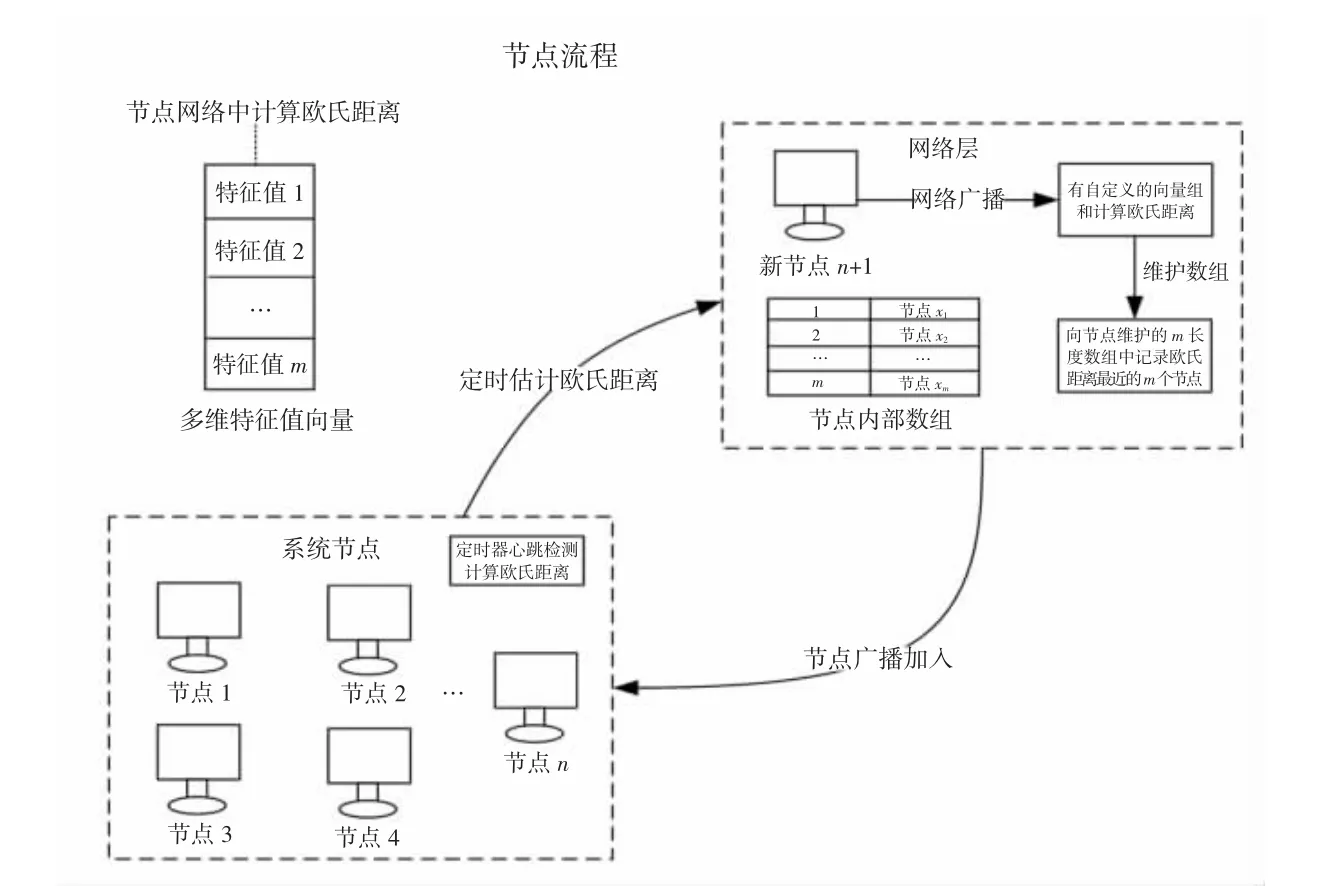
图3 算法的整体流程

经过上述流程后，每个节点会缓存欧氏距离近的节点，整个系统在选举和同步日志时会得到性能上的优化。领导者节点会根据内部的缓存数组来操作，节点压力也会减轻。详细过程如下：首先根据每个节点的内部数组进行选举；其次，若获得足够选票节点可直接当选，若不够则通过P2P 网络全局获取选票；最后再通过内部数组同步日志，同步过的节点再调用其内部数组记录同步日志直到全局完成日志同步。领导者节点的操作见图4。

图4 算法优化示意

2.1 算法多维向量处理过程

2.1.1 特征值提取为特征值向量 在初始化一个节点时，首先依据业务的要求进行数据挖掘，定义m 个特征值T＝｛t1，t2，t3，…，tm｝，并且根据它的重要性乘上相应的权重系数｛ρ1，ρ2，ρ3，…，ρm｝，最后得到特征值向量为｛ρ1t1，ρ2t2，ρ3t3，…，ρmtm｝，简化表示为：

得到的向量值存入节点对象的dis 字段中。依此类推遍历对所有节点进行向量的计算组合。

2.1.2 对特征值向量计算欧氏距离 在所有节点得到了m 个特征值向量之后，进入整个系统的初始化，即所有节点开始广播数据两两传递它们的特征值向量和节点的标识信息id。计算出它们相互之间的欧氏距离：

得到了整个欧氏距离d（x，y），在节点内部开辟一个长度为m 的数组（m 根据节点规模和工程需求来定），根据需求取n 个d（x，y）的值最小的节点id放入数组dis［］，数组中遍历节点可以充分利用CPU 的步长特性。算法的复杂度为O（1）级别，有利于后续的取数据运算。2.1.3 节点中设置过滤器 由于节点广播的时候可能会重复收到同一节点的信息，并且由于欧氏距离的运算较为复杂，所以使用过滤器来过滤相同标识节点发送的信息可以减少节点间的压力。如果数据量较小，可以采用位图方式构建的Bitset 数据结构。若数据量很大，则可以采用布隆过滤器（bloom filter）的方式。这两种数据结构都可以压缩数据，并且由于采用二进制运算，所以运行速度也比较快。

Bitset 和布隆过滤器的作用都是判断一个元素是否已经存在于集合中。这里以Bitset 为例解释。在节点广播信号中存放节点id，接收信号时如果id 之前没有接收过，则放入到Bitset 中；如果接收过，通过id 和Bitset 中的数据比较可以快速判断节点存在于集合中而不再进行其他操作。位图的原理是将整数x 作为一个bit 数组的下标存放于a[x]的bit 数组中，而一般的int 类型在计算机中占32 个bit，所以存放bit 大大地节省了内存空间。同理布隆过滤器底层也是位图，通过对数据进行多次哈希映射得到对应数组。布隆过滤器存在一定的误判率，但是只会误判已存在集合的数据而一定不会误判不存在的数据，且误判的概率非常小，可以忽略。

2.2 选举过程当在整个Raft 算法的系统中出现领导者节点宕机的情况下，未接收到返回心跳信号的节点发生状态机改变成为候选者节点发起选举。在选举的过程中，任意的候选者节点都会首先遍历节点内部dis［］数组，通过RPC（remote procedure call）方式发起拉票请求RequestVote，由于欧氏距离近的节点在通信速度和可靠性方面要强于欧氏距离远的节点，所以达成共识的速度会加快。在CFT算法达成共识的过程需要节点能更快交互，所以可以根据经验和系统的节点数对dis［］数组的长度m设置为一个特定的值以加快选举速度，但是这个过程需要和下面的日志复制过程综合考虑。

在获取选票过程中成为候选者状态的节点首先遍历自身dis［］中的节点，但是此节点不一定会获得超过半数的选票，所以还需要进行下一轮的Raft选举来实现原始获取选票的目的。在Raft 算法过程中加入过滤器避免重复选举请求消耗整体资源，让整个系统的性能得到优化。这里给每个节点在RequestVote 带上节点id 作为主键，让Bitset（或者布隆过滤器）来过滤请求，避免重复请求消耗系统资源。

综上整个选举过程分为两个部分，即内部近距离投票和全局投票，节点选举成功的概率可以如下表示：

其中m 为dis［］长度，n 为节点总数。

由于m 个节点的交互速度总体是高于全局的Raft 算法选举，所以算法选举的过程是快于原始算法的。

2.3 日志复制过程在日志复制过程中，同样采用就近节点的原则。通过内部dis［］数组的值，优先找到欧氏距离近的节点，进行日志复制操作AddEntities，步骤如下：

（1）首先领导者节点发送第一轮日志条目给欧氏距离近的m 个节点，由于欧氏距离近，其平时运行时的日志条目通常会比较相近，需复制的日志条目不会太多。

（2）相邻节点得到新的日志条目后，再根据它们内部的dis［］数组来发送相应的日志条目给欧氏距离较近的节点，依此类推。

（3）得到了新版本日志条目的节点会对这一次收到的版本号进行记录。其他节点发送心跳信号时，未同步节点给领导者节点发送信号进行第二轮的日志复制。这样就可以恢复到系统之前的日志状态。

2.4 新节点加入与定时心跳数据设置对于新加入的节点，首先，向已存在节点发送特征值向量请求计算欧氏距离的广播信号；其次，将得到的欧氏距离d（x，y）选取最小的若干值设置到自身dis［］数组；最后对整个系统进行其他的Raft 心跳操作。

其整体运算为串行，消耗运算时间为

其中，T 为消耗的总时间，t 为每个节点消耗的时间，n 为第n 个节点。

依据Raft 算法的定时器机制会设置范围在［150，300］的随机延时来发送心跳数据包，其中包含有领导者节点的任期和日志条目数量等，然后节点再对发送心跳信号的节点进行回复。在这个过程中可以设置一个较长时间的定时器，在一个非峰值的时段内发送心跳数据的同时对节点中的向量进行广播，重新调整欧氏距离，并且依据欧氏距离的大小重新调整内部的dis［］数组内容。其运算为并行的计算，时间的消耗为：

其中，T 为消耗的总时间，t 为每个节点消耗的时间，n 为第n 个节点。

节点的同步压力为：

其中，Q 为总的节点压力，q 为每个节点的压力，n 为第n 个节点。

2.5 分布式理论验证上文已经提到过Raft 算法是BASE 理论的最佳实践，同样MV-Raft 算法也是满足BASE 理论的最佳实践，并且可以提高BASE理论的相应性能。分析如下：在选举和日志复制的过程中优先选择欧氏距离较近的节点，可以提高基本可用的性能。优先选择欧氏距离近的节点不但可以减轻一块区域中的节点带宽压力，且由向量的计算后欧氏距离近节点日志的差异小，进行日志复制时节点之间需要传输的日志条目减少，提高了可用性。在领导者节点崩溃后，同一时间相近区域内出现候选者的概率会相对减少，使得软状态切换也减少，节点中状态切换的可能性变低，这会加快选出新领导者节点的过程，让最终一致性能更快实现。

上述的这些优化结果都是在选取了正确特征值的条件下产生的。在日常的开发过程中，选择特征值需要根据实际场景来确定。例如在HyperLedger Fabric 中需要考虑节点的机构信用担保授权（即背书）情况，每个节点的背书使得该节点拥有不同的权值。给不同节点的背书确立相对应的分数编入多维向量，在计算欧氏距离中得到很大的体现，使得整体系统的网络速度加快。

3 算法实现及性能分析

3.1 算法实现过程本实验将按照如下5 个步骤进行实验：

（1）创建一个三维数组vector 的变量放入节点中，变量为随机数产生，其中数据类型为float64 其值介于［0，1］。

（2）通过遍历所有节点，计算欧氏距离，取6 个最小数。

（3）将以上的6 个数放入dis［］数组中，同时将这6 个数的id 放入节点的ids［］数组中依据数组下标来一一映射。

（4）在选举的交互过程中，利用双方的vector 设置模拟延迟数据，进行测试。内部保存欧氏距离的节点属性dis［］数组长度将参数设置为6 用来实验。

（5）在领导者节点当选之后，发送领导者节点日志复制信号，从所有节点设置为从ids［］数组中取得，然后再递归调用日志复制。

本文实验采用Go 语言来实现Raft 算法并加以改进，通过上述的参数来设置Raft 算法的多维向量。运用多轮模拟选举和日志复制的过程来实验，观察领导者节点的选举消耗时间，以及日志复制对各个节点的压力。

3.2 实验结果与分析Raft 算法由于需获得过半投票才能当选，所以节点数一般要求是奇数。对奇数个节点采取随机抽样检验方式搜集数据。下面列出MV-Raft 算法中节点选举的比较数据，统计图见图5。

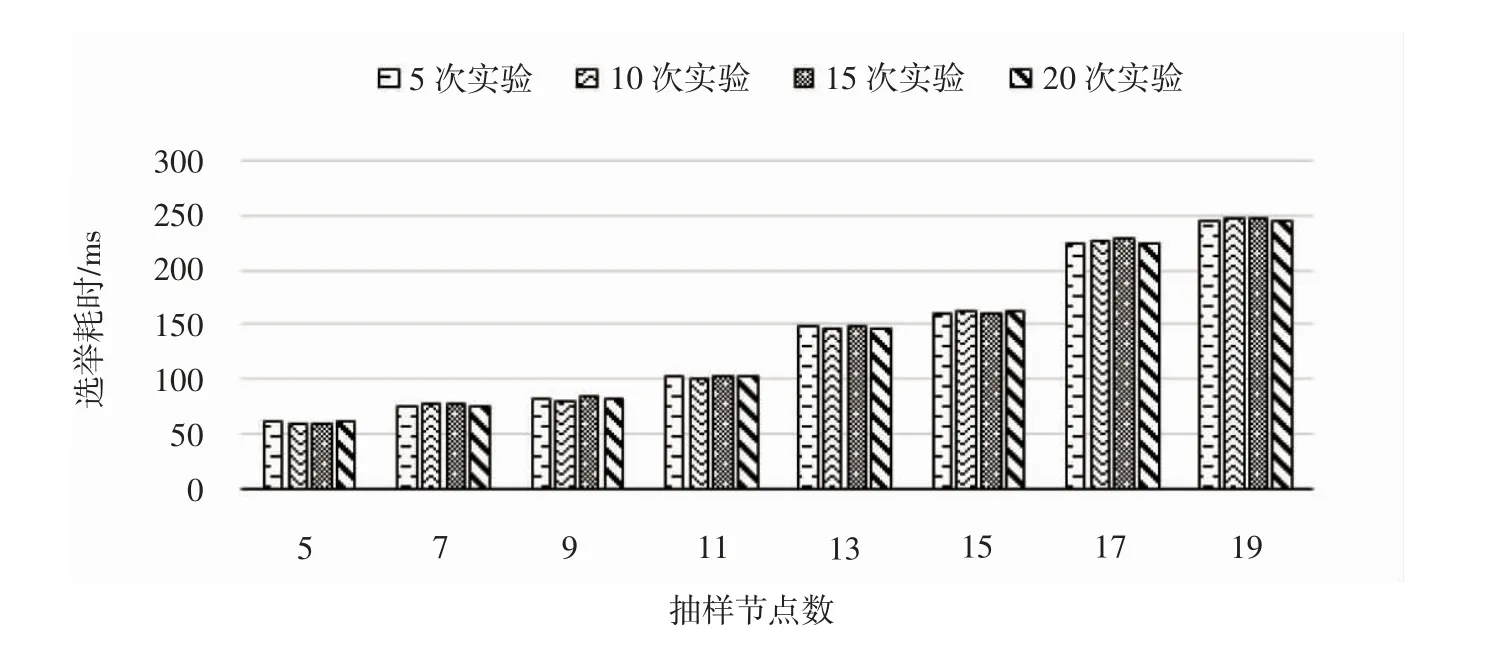
图5 MV-Raft 算法平均耗时柱状图

由于Raft 算法的定时器机制会带来数据波动，节点少会让算法耗时不明显，节点多会让并发加大使得数据偏差变大，所以选择中位数11 个节点来测试。通过测试的中位数和原始Raft 算法做比较，通过10 次选举后做出对比，见图6。

图6 选举耗时柱状图

由于Raft 算法具有随机定时器机制，选举耗时具有一定的波动性造成单次选举耗时也出现波动。在统计平均值后得出，原始Raft 算法平均耗时118 ms，而MV-Raft 算法平均耗时99 ms。以上结果证明，改进后的MV-Raft 算法在选举的整体效果中要优于原始Raft 算法。MV-Raft 算法相较于原始Raft算法选举耗时减少16%，整体显示出来MV-Raft 算法的平均数据更好。

在节点的日志复制过程中，首先是寻找欧氏距离较近节点。对于领导者节点的压力可以相对于原有算法的节点数减去ids［］数组的长度。欧氏距离较近节点之间传输数据会较快，此处采用的方式是P2P 的Gossip 协议的算法，节点是通过push 的方式同步数据，在一轮的同步中节点被同步的概率为（每个节点在每个周期被感染的概率都是固定的p，其中0＜p＜1，因此Gossip 算法是基于p 的平方收敛，也称为概率收敛）：

在每一轮的同步过程中原始算法的领导者节点是全节点同步压力随着节点数的增加呈线性增长的，MV-Raft 算法由于内部缓存节点固定为5 个，所以领导者节点的压力固定为5 没有变化。数据测试压力见图7。

图7 系统节点同步次数

本文对Raft 算法进行研究，提出一种基于多维向量的Raft 算法——MV-Raft。MV-Raft 算法通过业务需求权重计算获取多维向量并计算其欧氏距离，使得在领导者节点选举和日志复制方面有效地提高整体性能，并且减轻节点的压力使得系统不易崩溃。本文提出的多维向量机制需要根据业务的实际需求来确定特征值，未来的研究中将进一步针对文中的参数调整使用机器学习的方法搜集大量业务数据做出新的研究。