核心概念统领下的高效小学数学单元整体教学
王延河

摘要:本文以“多边形面积”单元为例,从学生和学科两个维度出发,深度分析学生认知起点与教材结构,尝试在核心概念的统领下,重组教学结构,以单元整体推进的方式,使学习内容系统化、学习方式整体化、学生思维发展结构化。
关键词:单元教学整体教学核心概念
1932年,美籍奥地利生物学家贝塔朗菲首次提出了系统论思想。该理论的核心思想是系统的整体观念,认为任何系统都是一个有机的整体,系统中各要素不是孤立存在,而是相互关联,构成一个不可分割的整体。系统论思想注重的是部分与部分之间的沟通和联系,强调整体思维和结构合理、功能完善,认为只要结构功能完善,则整体功能就会大于各部分功能之和。
如果将数学课程看作一个系统,那么单元就是课程系统中的一个子系统,课时是这个子系统的要素。教学不仅要关注课时的目标和内容,更应重视对单元内容的整体把握。通过研究部分与部分间的关系,优化整体的结构和功能,以实现“整体大于部分之和”。
所谓“核心概念”,笔者的理解是依据部分之间的联系和共性,提炼出的核心思想和方法。它不仅是一种联结,是学科内容的核心,而且是持久的、可迁移到新的情境中去。教师站在“某一领域”或“某一主题”的视角,围绕“核心概念”,对单元内容进行梳理和重组,分析学情,确定单元的整体目标,设计单元整体教学,以单元结构的优化带动课时结构的优化。
本文以“多边形的面积”单元为例,阐述笔者对于单元整体教学的思考。
一、思考:解读学生与教材,反思传统结构
(一)了解学生的“最近发展区”,明确教学重点
首先,三年级学生已掌握面积的相关知识,会测量简单平面图形面积的大小,能计算长方形面积,并理解其中的道理。其次,通过访谈和调查发现,已知晓平行四边形、三角形和梯形的面积计算方法的学生超过50%,了解计算公式原理的占三分之一左右,但对于所有图形的面积都是面积单位的累加这一实质的了解较少。由此发现,学生不是零起点。因此,明确什么不需要教、什么需要教、什么要重点教,是展开教学的依据。
(二)找出单元教学联结点展开教学
本单元是面积教学的第二阶段,在该阶段教学中我们发现,任意一个图形都可以通过转化成其他图形来求面积。这些图形之间是有联系的。那教材为什么将长方形的面积作为面积计算的起始课呢?笔者认为这是由面积的本质决定的。
面积是指图形中包含面积单位的个数,无论是长方形、正方形、平行四边形、三角形、梯形,还是圆形、不规则图形,所有图形的面积皆是如此。长方形由于其图形的特征,所包含的面积单位的个数最容易数,而其他多边形的面积包含的面积单位的个数不方便直接数,需要通过割补、拼组等方式将面积单位规整。正因如此,才产生了化归思想。同理,第三阶段圆的面积计算,其实质也是数面积单位的个数,不过化归更为简便。但不论直接数,还是先化归再计数,本质都是面积的度量。
找到化归思想背后的原理,明确三个阶段教学的联结点,我们选择“面积单位的计数”(即“度量”),作为本单元的核心概念。尝试在面积度量的统领下,整体学习有关平面图形面积的知识,然后有结构、有重点地展开不同图形的面积学习,前联后延,聚焦核心,整体把握,以便将学习经验和能力更好地迁移到其他主题的学习中去。
(三)反思教材编排
通过对本单元五个例题的对比、分析和梳理,我们发现前三个例题“平行四边形的面积”“三角形的面积”“梯形的面积”都是按照图形转化—公式推导—公式运用的路径进行教学的。这时我们需要思考:学生经历三次相同的学习历程,是否还能保持最初的兴趣和动力?三个例题都呈现出“重化归方法,轻原理探索”的特点,这是否有利于学生理解多边形面积的本质?
有教师试图把三个例题中的两个或者三个合在一起教学。但若不改变传统教学路径和学习方式,其实质只是简单的课时拼凑,并非真正意义上的整合。整合的内涵是结构优化。以“度量”为统领,将三个内容整合教学,既可以增加学习的效度和深度,又可以促进学生的学习方式从碎片化转向整体化。这也正是“系统论”所倡导的只要结构合理、功能完善,则整体功能就会大于各部分功能之和。
二、实践:核心概念统领下的单元整体教学
笔者认为“多边形面积(一)”是本单元的种子课,随着单元教学框架的调整,本节课教学结构有了很大变化。因此,笔者对本课时进行了重点研讨与课堂实践。
(一)教学目标再定位
将三节课整合成一个课时,课堂容量大大增加,因此笔者对课时目标进行了筛选。这节课的主要目标就是多层次经历“数面积单位的个数”,感悟面积本质。具体实践过程如下:(1)任务驱动,在计算面积的过程中,感悟转化的道理,即面积单位归整的必要性;(2)经历转化过程,在面积单位归整的过程中进一步体会面积的本质;(3)培养数学思维,发展空间观念。
(二)教学环节
1.开门见山,导入新课
师:我们学习过哪些平面图形?
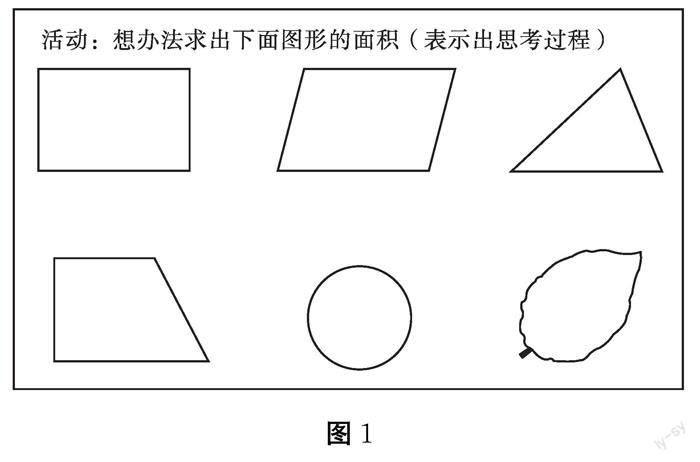
出示任务:你有办法求出这些平面图形的面积吗?请你想办法求出它们的面积,并且把你的想法完整地表示出来,让大家都能看明白。如下图1 所示 :
注:整体呈现,大任务驱动,引发学生思考。
2.教师巡视,收集学生的想法。
3.交流反馈。
师:整体观察,以平行四边形面积切入,你不赞成哪种方法?说明道理。
生1:我不赞成“底×邻边”计算面积的方法,我觉得這样算出来的面积比实际面积要大。
生2:平行四边形会变形,我们想象这个平行四边形是个框架,拉一下,它就变成一个长方形,面积变大了(见图2)。
注:引导学生发现问题,理解“底×邻边”的计算方法算得的面积变大。
师:为什么平行四边形的面积可以用“底×高”来计算?
生1:因为平行四边形可以“割补”成长方形,面积不变,长方形的长即平行四边形的底,长方形的宽即平行四边形的高……
注:使学生体会转化的价值和过程,找到平行四边形和长方形的联系,并推导公式。
师:长方形的面积大家都很清楚,那你们还记得当初我们是怎么研究出“长方形的面积=长×宽”的吗?
生:我们是数小方格的。一行几个,有几行。
……
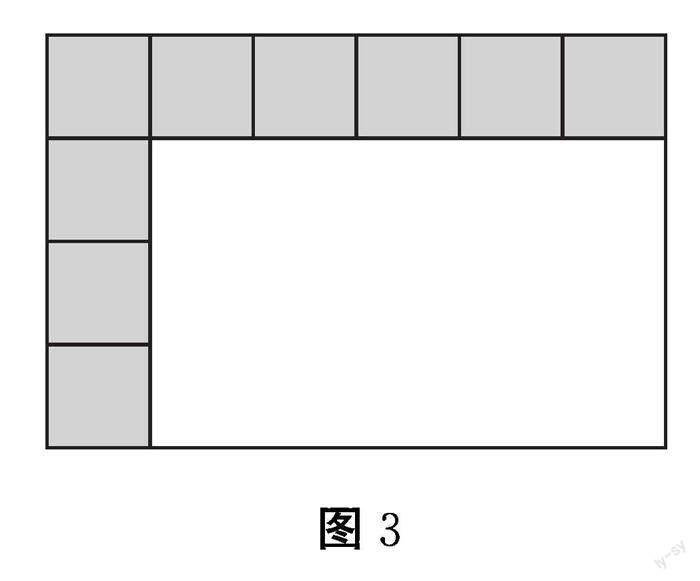
师:是这个意思吗?这些小方格的面积是1平方厘米,数一数有几个,就知道图形面积了,后来我们发现用“长×宽”的方法数得更快,就发明了这个计算方法(见图3)。
注:通过回忆长方形的面积探究过程,唤起学生的经验,初步感悟面积的本质。
师:为什么计算平行四边形的面积不能像长方形一样数数有几个1平方厘米小方格,而要这样转化呢?
生1:平行四边形的一条边是斜的,如果把它左边的直角三角形剪下来拼到右边,变成长方形就方便计算了(见图4)。
生2:是的,不然就得把小格子一个一个拼起来数,太麻烦了。
师:我听明白了,直接数这里有几个1平方厘米有点困难,所以大家想到了拼方格的办法,最好就是这样整块拼。原来,我们研究平行四边形的面积时先把它转化成长方形是这个道理呀!
注:通过提问来引导学生,使学生在辨析中感悟面积本质。
4.迁移学习
师:知道了求平行四边形面积的方法,现在你能用这个方法再来求其他图形的面积吗?
注:学生在互动中进一步感悟面积本质,体会化归思想,并得出三角形、梯形的面积计算方法。
5.对比总结
师:通过今天的学习,大家知道了多边形面积的计算方法。你们觉得这些图形的面积的求法有什么相同的地方吗?
总结:不论什么图形的面积其实都是数里面有几个小方格,有的可以直接数,有的需要先进行转化再数。其实在生活中,除了面积,还有许多这样的内容,如长度、角度、时间等。
三、反思:深度理解,实现迁移
(一)构建单元结构化教学实施框架
单元整体备课是进行单元整体教学的前提。如何对单元教学目标、教学内容、教学过程、教学方法等要素进行系统分析、优化组合、整体设计?我们尝试从学科和学生两个维度入手,具体操作如下(见 图5) :
(二)从小单元延伸至大单元,基于核心概念进行深度学习
单元既可以是教材中已经确定好的某个教学单元,即“小单元”,也可以是几个教学单元组成的“大单元”。教师依据小单元之间的共性进行大单元 教学 。
比如“多边形的面积”教学,就是从大单元视角,将不同年段的三个面积教学单元适度整合起来,找到单元之间的内在联系,提炼出核心概念——“度量”,首先确定一个具体的学习目标,然后寻找实现目标的教学路径。“多边形的面积”单元的教学实践,正是基于“以终为始”展开设计,对单元的预期结果先做好规划,再进行教学。正因有了核心概念的引航,学生的学习目标才更明确,对内容的理解才更深刻。
(三)实现迁移,真正落实数学素养发展
单元整体教学的目的就是从根本上提高学生的素养。学生的素养体现为在新情境中解决问题的能力,即学习经验和学习能力的迁移。能力迁移是学习的长期目标,是在真正理解的基础上进行的。我们需要依靠“核心概念”来组织教学,以单元教学为载体,促进学生深层次学习,加深对知识的理解,这样才能在新情境中实现迁移。
正如“多边形的面积”单元,在“度量”的统领下,通过结构化的单元教学,学生不仅对“多边形的面积”有了深层理解,而且对数学课程中的“度量”概念有所感悟。比如长度就是长度单位的累加,角度就是幾个1度的累加,时间则是时间单位的累计,等等。有了这样的理解,学生才能在具体生活或实际情境中灵活运用知识,举一反三。
综上所述,在新课程背景下,如何以整体性视野来整合资源、设计教学是值得教师思考和研究的。我们基于学科逻辑和学生立场两个维度,确定教学重难点,创造性地打破教材原有顺序,重组、优化教学结构,使得知识脉络更加清晰,这样学生的学习也更有挑战性。但值得关注的是,我们在具体实施过程中不能只关注单元重点课时,对于跟进、补救课时应同样做到有选择、有挑战、有提升,更要在教学中时时关注每一位学生的实际学习状态及学习效果,发现问题,及时调整,寻求更优策略和路径,以达到预期的教学目标。
参考文献:
[1]格兰特·威金斯,杰伊·麦克泰.理解为先模式——单元教学设计指南(一)[M].盛群力,沈祖芸,柳丰,等译.福州:福建教育出版社,2018.
[2]朱国平.基于结构化的小学数学课堂[M].杭州:浙江教育出版社,2017.
[3]陈瑞刚.基于“结构化”视野的小学数学课堂教学重构[J].数学教学通讯,2018(19):11-12.
责任编辑:唐丹丹

