基于McDiarmid 边界的自适应加权概念漂移检测方法

胡 阳，孙自强

（华东理工大学能源化工过程智能制造教育部重点实验室, 上海 200237）

智能手机、运动手表、便携式电脑等各种互联网设备已经成为人们必不可缺的物品，部署在这些设备上的传感器时刻感知周围的信息，如汽车的环境温度、湿度和两车间距等。海量的信息被传感器采集，以数据流的形式实时传输到终端进行处理分析，挖掘出潜在的信息。随着信息技术的发展，越来越多的场景不仅面对静态数据，还需要面对不断到来的动态数据。因为数据流的持续抵达、高基数、统计特征变化等特点，数据处理需要在有限的计算和内存资源下，实时处理大量数据，并且能适应数据流发生的概念漂移，显然传统的数据挖掘方法不再适用。

概念漂移是指数据流的统计特征随时间的变化。在考虑数据流分类问题时，需要思考如何设计概念漂移检测器。概念漂移检测器可分为两类：第一类是在发生数据流变化时进行标记，并允许做出一些反馈，让分类器适应数据流的变化，这类检测器可以和分类器分开设计；第二类是检测器与分类器一起设计，是分类器的一部分，即分类器自身就有适应数据流变化的能力，不需要检测数据流中是否存在概念漂移。概念漂移检测方法可分为主动方法和被动方法[1-3]，两者的区别主要有3 点：第一，主动方法包含检测机制和适应机制，在检测到数据分布变化时对模型进行调整或者重建，通过判断数据流中分类器的性能改变幅度是否超预定阈值来判定概念漂移的发生。被动方法只有适应机制，不检测数据流中是否存在概念漂移，而是根据数据流的变化不断地调整模型以适应环境。第二，主动方法适合处理突变型概念漂移，被动方法适合处理渐变型和重现型概念漂移。第三，主动方法适用于在线学习的框架中，而被动方法常用于基于块的学习框架中。Yu 等[4]将主动检测方法分成了3 类：第一类是基于错误率的概念漂移检测方法；第二类是基于数据分布的概念漂移检测方法；第三类是多假设检验漂移检测方法。基于错误率的检测方法以PAC（Probably Approximately Correct）学习理论[5]为基础，在假设样本分布平稳的前提下，通过分析模型性能指标是否超过某一阈值以判断概念漂移的发生。Gama 等[6]提出了DDM（Drift Detection Method）方法，假定测量值服从伯努利分布，当样本量足够大时，二项分布将近似于高斯分布。该方法保留错误率的均值和方差的历史最小值，并设定警告边界和漂移边界，若当前错误率超过设定的阈值，则给出相应反馈。当概念较长时，DDM 算法具有较高的检测延迟。为解决这一问题，Barros 等[7]提出了RDDM（Reactive Drift Detection Method）算法，该算法为降低检测延迟，丢弃了较长概念的旧样本。然而，RDDM 舍弃大量旧样本会导致模型泛化能力变差，出现较多的漏检、误报。为了提高检测性能，Frias-Blanco 等[8]提出了HDDM（Drift Detection Method based on the Hoeffding’s inequality）算法，该算法假设检测值是独立随机的有界变量，利用Hoeffding 不等式得到类Ⅰ和类Ⅱ错误率的统计检验边界，以 1-δ 的概率对结果进行保证，并提出两种方法分别检测突变和渐进型漂移。Pesaranghader 等[9]在HDDM 算法中引入了滑动窗口，提出了FHDDM（Fast Hoeffding Drift Detection Method）算法，其相对于HDDM 算法减少了漏检、误报，但检测延迟更高。

目前，主动检测方法主要存在两个问题：第一，大多数主动方法处理概念漂移有较大的检测延迟；第二，主动方法更适用于处理突变型概念漂移，处理渐变型概念漂移会出现较多的误报、漏报，影响分类器性能。本文从以上两点出发改进主动方法，提出了基于McDiarmid 边界的自适应加权概念漂移检测方法（WMDDM）。WMDDM 通过衰减函数对分类结果加权，并根据反馈的检测信号实时调整模型，提高模型对数据流的适应能力。实验结果表明，WMDDM能降低检测延迟、误报率和漏检率，并且能适应多种类型的概念漂移，提高分类器性能。

1 基于Hoeffding 界的漂移检测方法

1.1 概念漂移

贝叶斯决策理论通常根据分类的先验概率分布p(y)和条件概率分布p(X|y) 描述分类过程，分类决策与类别的后验概率有关。给定样本X，类别ci相应的后验概率为：

概念是指样本在某一时间点的整体分布 P ，P的改变称为概念漂移。若t1时刻，存在随机变量X使得式(2)成立，t1时刻前后数据的联合概率分布不同，P 发生改变，t1时刻出现概念漂移。

根据分布情况的变化，概念漂移可分为实漂移和虚漂移两种类型[10]。如图1 所示，图1(a)所示为两类数据的初始分布，经过一段时间后，整体分布变为图1(b)示出的分类边界发生变化而数据分布不变，这种变化称为实漂移。若经过一段时间后，分布变为图1(c)示出的分类边界不变而数据分布发生改变，则称这类变化为虚漂移。

图1 实漂移和虚漂移概念图Fig.1 Conceptual diagram of real drift and virtual drift

根据概念的变化率，可将概念漂移分为突变型漂移、渐进型漂移、增量型漂移和重现型漂移[3]。图2(a)所示为突变型漂移，表示数据分布突然发生改变。图2(b)所示为渐进型漂移，类1 逐渐减少，类2 逐渐增多，导致分布差异不断变大，直到类2 取代类1。图2(c)所示为增量型漂移，其变化率较小，两个数据分布的差异变化不显著。图2(d)所示为重现型漂移，指先前的概念在之后某个时间又再次出现。

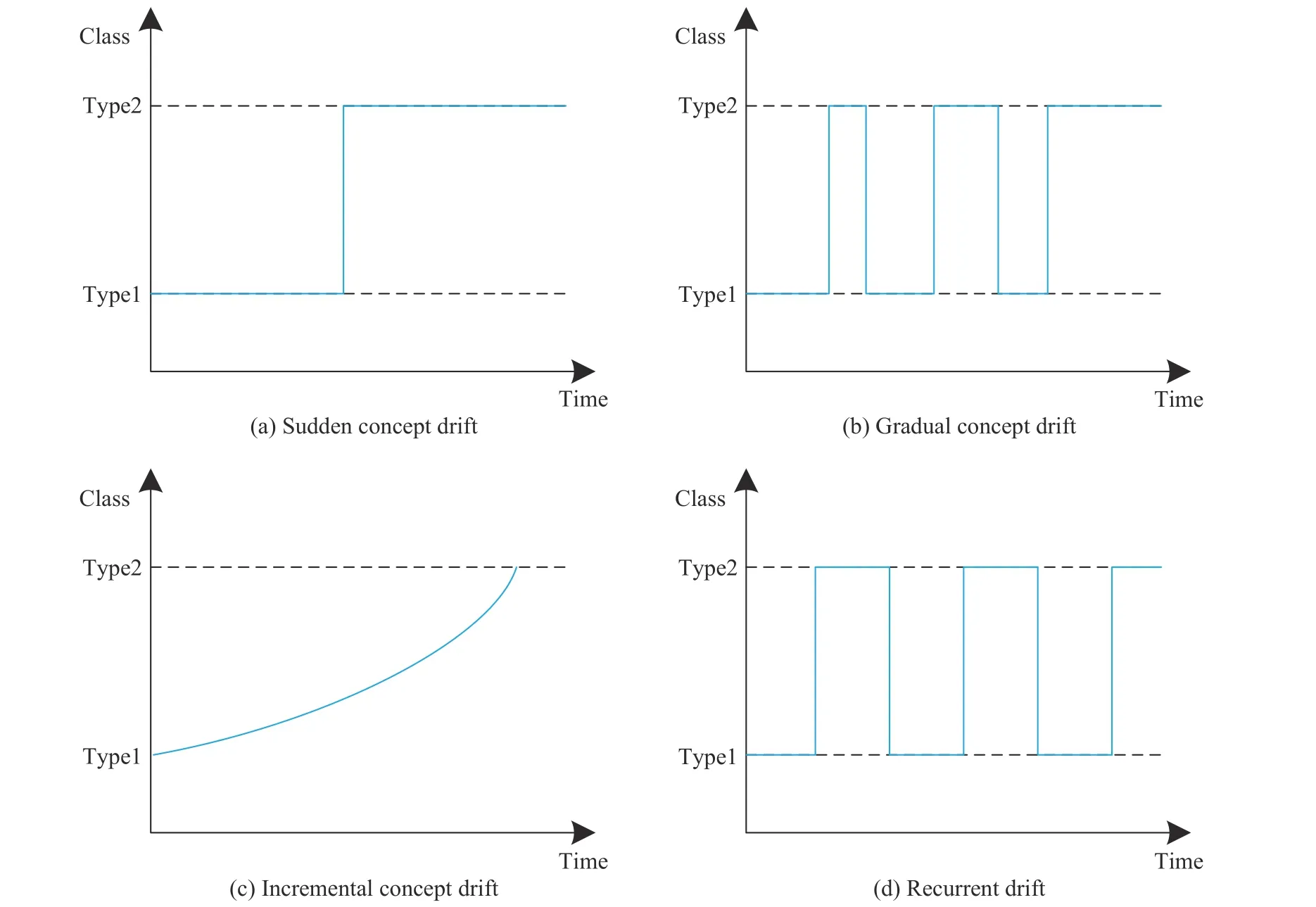
图2 概念漂移类型图Fig.2 Concept drift type diagram

实际数据流中，概念漂移一般是混合出现，即多种类型的概念漂移可能出现在同一流中，理想的概念漂移检测器应能适应多种类型的概念漂移。

1.2 FHDDM 算法

根据计算机学习理论[4]，当假设空间h在数据集D的经验误差为0，则称h与D一致。然而，学习算法事先并不知道概念类C 的存在，在假设空间里不总能找到一个零错误率的假设，在考虑学习器有非零错误率假设时，需要找到一个边界来限定学习器所需的样本数量。

Hoeffding 不等式[11]刻画了某个事件的真实概率及与每个伯努利实验估计概率的差异。该不等式给出一个概率边界，并说明多少训练样本才足以保证真实错误率和训练错误率接近。

定理1（Hoeffding 不等式）：设X1,···,Xn是一列独立随机变量，且Xi∈[ai,bi] ，对于 ε ＞0 ，有：

式中：Pr表示概率值，E表示期望值。式(3)和式(4)中，样本均值显著性水平 δ 表示真实错误率和训练错误率不一致的事件发生的最大概率。给定显著性水平 δ 和样本量n，由式(2)可求出错误边界（Hoeffding 不等式得出）εδ：

FHDDM 算法通过固定大小的滑动窗口观察n个分类结果，根据式(5)得到 εδ，假设表示窗口在t时刻观测到的分类正确率，表示t时刻观测到的历史最大分类正确率。若，则未漂移；若≥εδ，则发生漂移。

2 基于McDiarmid 界的漂移检测方法

2.1 加权机制

流数据处理模型的核心思想是支持数据的在线持续处理，主要场景是处理无界数据[9]。大多数检测策略是维持一个固定窗口（如FHDDM 算法），这种检测策略会受到窗口大小的影响，大窗口可以降低误判次数，但检测延迟高；小窗口检测延迟低，但会增加误判次数，并对噪声敏感。因此，FHDDM 算法处理不同漂移类型数据集时需要调节不同的窗口值。若在检测过程中引入自适应更新规则，能提高检测效率和准确率[12-13]。

假设某分类器的分类结果如图3 所示，使用FHDDM 分别对分类结果和加权分类结果进行概念漂移检测，设n和 δ 分别为10 和0.2，由式(5)可求得错误边界 εd（McDiamid 不等式得出）为0.28。t/f表示分类结果（1 为正确，0 为错误），p是窗口左端滑动到序号i位置时观察到的分类正确率，pw是经过加权后的分类正确率，Δp=pmax-p，Δpw=pwmax-pw，真实漂移发生在序号i=12 处。使用Sigmoid函数w(x)计算各个数据的权值：

图3 加权窗口描述图Fig.3 Weighted window description diagram

若不考虑分类结果加权后的错误边界计算问题，观察图3 中的 Δp和 Δpw，FHDDM 在序号18 处检测到漂移。加权后，FHDDM 在序号17 处检测到漂移。考虑加权后的错误边界计算问题，Hoeffding不等式不再适用求解加权后的漂移边界。下面将介绍McDiarmid 不等式及错误边界的计算过程。

定理2（McDiarmid 不等式[14]）：设X1,···,Xn是一组独立随机变量，值域分别为R1,···,Rn。f:R1×···×Rn→R是一个满足独立有界差分条件的可测函数。设d=(d1,···,dn) 是f(Y) 与f(Y′) 的差异向量，若存在di＞0 ，∀xi,xi’(i=1,···,n) ，其他自变量不变，有：

那么，存在加权后的错误边界 εD＞0 ，满足：

定理2 的证明需要用到以下引理：

引理1（Hoeffding 引理）：令随机变量X满足E[X]=0且a≤X≤b，对于 ∀t＞0 ，有：

引理2（Markov 不等式）：对于非负随机变量X，有：

证明：设Vi=E(f|X1,···,Xi)-E(f|X1,···,Xi-1) ，其中E(Vi|X1,···,Xi-1)=0[15]，那么：

引理1 可变换成：

对于 ∀t＞0 ，

利用式(19)算得图3 中加权后的漂移边界εD=0.295 ＜0.316 ，在序号17 处能检测到漂移的发生。

2.2 WMDDM 算法

Bifet 等[16]提出的窗口（ADWIN）算法可自适应调节滑动窗口，当检测到警告信号时减小检测窗口。由于该方法摒弃一部分数据，会产生欠拟合导致模型泛化能力降低、误报次数增加且对噪声敏感。WMDDM 算法检测到警告信号时调节衰减参数λ、θ，调整模型以适应数据流的变化。

回顾式(6)，当 λ ＜1 时，w(x) 主要由 θ 调节，θ 越大，w(x) 下降速度越缓；当 λ ＞1 时，λ 越大，w(x) 下降速度越快。加权准确率pw由式(20)求得，f(x)={0,1}，1 表示分类成功，0 为失败。

如图4 所示，首先初始化WMDDM 检测器，将分类结果添加至滑动窗口，当数据量等于窗口大小时，计算pw并更新历史最大加权正确率。若pw＞，则未漂移；若-pw＞εdrift，将漂移信号反馈到分类器，并初始化检测器；若-pw＞εwarning，发出警告信号，调节衰减参数 λ、θ ，更新检测器。

图4 WMDDM 算法流程图Fig.4 WMDDM algorithm flow chart

3 实验与结果分析

MOA[17]（Massive Online Analysis）是一个基于Java 开发的数据流挖掘平台，该平台集成了各种数据流算法、数据流生成器以及评估机制。本节将WMDDM 与FHDDM、HDDM、DDM、RDDM 以及ADWIN 进行对比实验，从误报率、漏报率、平均检测延迟和分类正确率4 个指标验证WMDDM 的概念漂移检测性能，实验采用HT（Hoeffding Tree）和NB（Naïve Bayes）分类器。

3.1 评价指标

概念漂移检测通常采用真阳率（TP）、假阳率（FP）、假阴率（FN）和分类器的正确率作为评价指标，理想的检测器具有更高的TP 和更低的FP、FN，本文采用可接受延迟长度 Δ 来统计上述指标[8]。Δ用来定义检测到漂移的位置与漂移的真实位置间的最大距离，突变型漂移通常设置为250，渐进型漂移通常为概念长度的2%。检测点的表示如图5 所示。

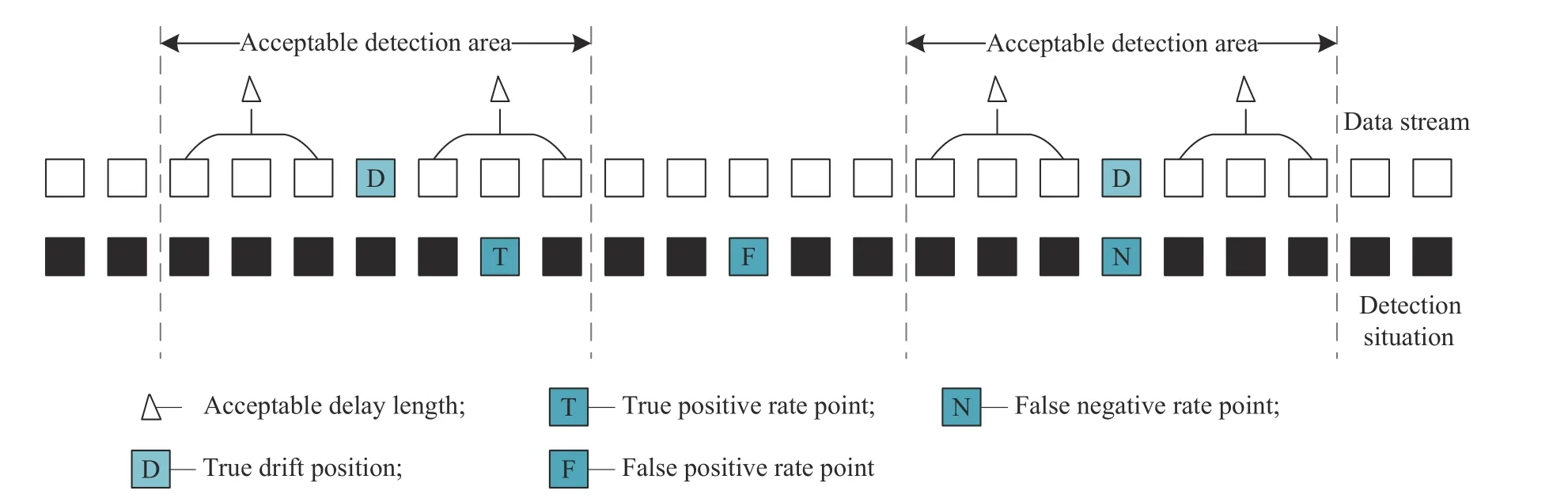
图5 检测点示意图Fig.5 Schematic diagram of detection points

TP 表示在 Δ 范围内检测到漂移的个数；FP 表示在 Δ 范围外检测到漂移的个数；FN 表示在 Δ 范围内没有检测到漂移的个数。因此，误报率（FPR，False Positive Rate）和漏报率（FNR，False Negative Rate）分别为：

平均检测延迟（Average Delay of Detection，ADOD）评价检测速度，若Di表示第i个漂移发生的位置，D′i表示漂移被检测到位置，n'为检测到的漂移个数，则：

3.2 数据集介绍

本文使用4 个人工数据集和1 个真实数据集测试检测器的性能，如表1 所示，人工数据集有：

表1 数据集特征表Table 1 Data set feature table

SINE：包含突变漂移的数据集，具有x、y两个属性。函数y=sin(x) 对样本分类，样本被正弦曲线分为上下两类，分别用正负号标记，每达到一次漂移点，两类的正负标记交换。每20 000 个样本出现一次漂移，共100 000 个样本，产生4 次漂移。

MIXED：包含突变漂移的数据集，具有两个布尔属性和两个连续属性x、y。当属性值满足{true，true，y ＜(0.5+0.3*sine2πx)}时，样本被标记为正，否则为负。数据含有10%的噪声，且每20 000 个样本出现一次漂移，共100 000 个样本，产生4 次漂移。

LED：包含渐进型漂移的数据集，是由LED 生成器生成、用于预测七段二极管上显示的数据集，具有24 个属性和10 个类别。每25 000 个样本出现一次渐进型漂移，共100 000 个样本。

CIRCLE：包含了渐进漂移的数据集，由4 个圆形方程表示4 个不同概念，分别为＜(0.2,0.5)0.15＞、＜(0.4,0.5)0.2＞、＜(0.6,0.5)0.25＞和＜(0.8,0.5)0.3＞，圆内标记为正，圆外为负。数据含有10%的噪声，且每25 000个样本出现一次漂移，共100 000 个样本，产生3 次漂移。

表1 示出的真实数据集为Electricity：该数据集是来自澳大利亚新南威尔士州电力市场，其能源价格受市场需求、供给、季节和天气等因素影响的数据，用来测试检测器在真实数据中的效果，表中共有45 312个样本，每个样本具有7 个属性和2 个类。

3.3 自适应权重有效性

为验证自适应加权的有效性，本节将WMDDM与不含自适应机制的WMDDM#1 以及FHDDM 算法进行对比实验，实验分为2 组。实验1 使用SINE数据集，NB 分类器，滑动窗口为100，初始参数为θ=100、λ=0.5 ，δdrift=0.001 ，δwarning=0.005 ，Δ=250 。实验1 结果见表2。由结果可得，在平均检测延迟和正确率方面，WMDDM 优于FHDDM。在误报率方面，WMDDM算法与FHDDM 算法都没发生误报，而WMDDM#1误报率高。实验2 使用CIRCLE 数据集，Δ=400，其他设置与实验1 相同。实验2 结果见表3，在平均检测延迟和正确率方面，WMDDM 优于FHDDM。虽然WMDDM#1 平均检测延迟最低，但误报率高。综合两组实验结果，在两种不同漂移类型的数据集上，WMDDM 的性能优于FHDDM，且不存在误报、漏报，而WMDDM#1 的误报率高。因此，自适应调节衰减函数能降低检测延迟，减少误报。

表2 实验1 结果Table 2 Results of experiment 1

表3 实验2 结果Table 3 Results of experiment 2

3.4 算法性能对比

本节将WMDDM 与FHDDM、HDDM、DDM、RDDM 及ADWIN 等算法对比，分别用于HT 和NB分类器，4 个人工数据集上的实验结果见表4～表7。由结果可知，WMDDM 与FHDDM 比较，二者在4 个数据集上没有发生漏检，WMDDM 在4 个数据集的误报率、平均检测延迟和分类正确率高于或等于FHDDM。WMDDM 与HDDM 比较，无论分类器采用HT 还是NB，WMDDM 在LED 数据集上取得最低的平均检测延迟和最高分类正确率。HDDM 的误报率和漏报率在MIXED、LED 和CIRCLE 数据集上高于或等于WMDDM。DDM、RDDM 和ADWIN 在4 个数据集上具有较高的误报率、漏报率和平均检测延迟。综上所述，WMDDM 在不同数据集上都能取得较好的结果，具有最低的误报率和漏检率，且平均检测延迟和正确率在6 种算法中排前2。

表4 在SINE 数据集上的实验结果Table 4 Experimental results on the SINE dataset

表5 MIXED 数据集上的实验结果Table 5 Experimental results on the MIXED dataset

表6 LED 数据集上的实验结果Table 6 Experimental results on the LED dataset

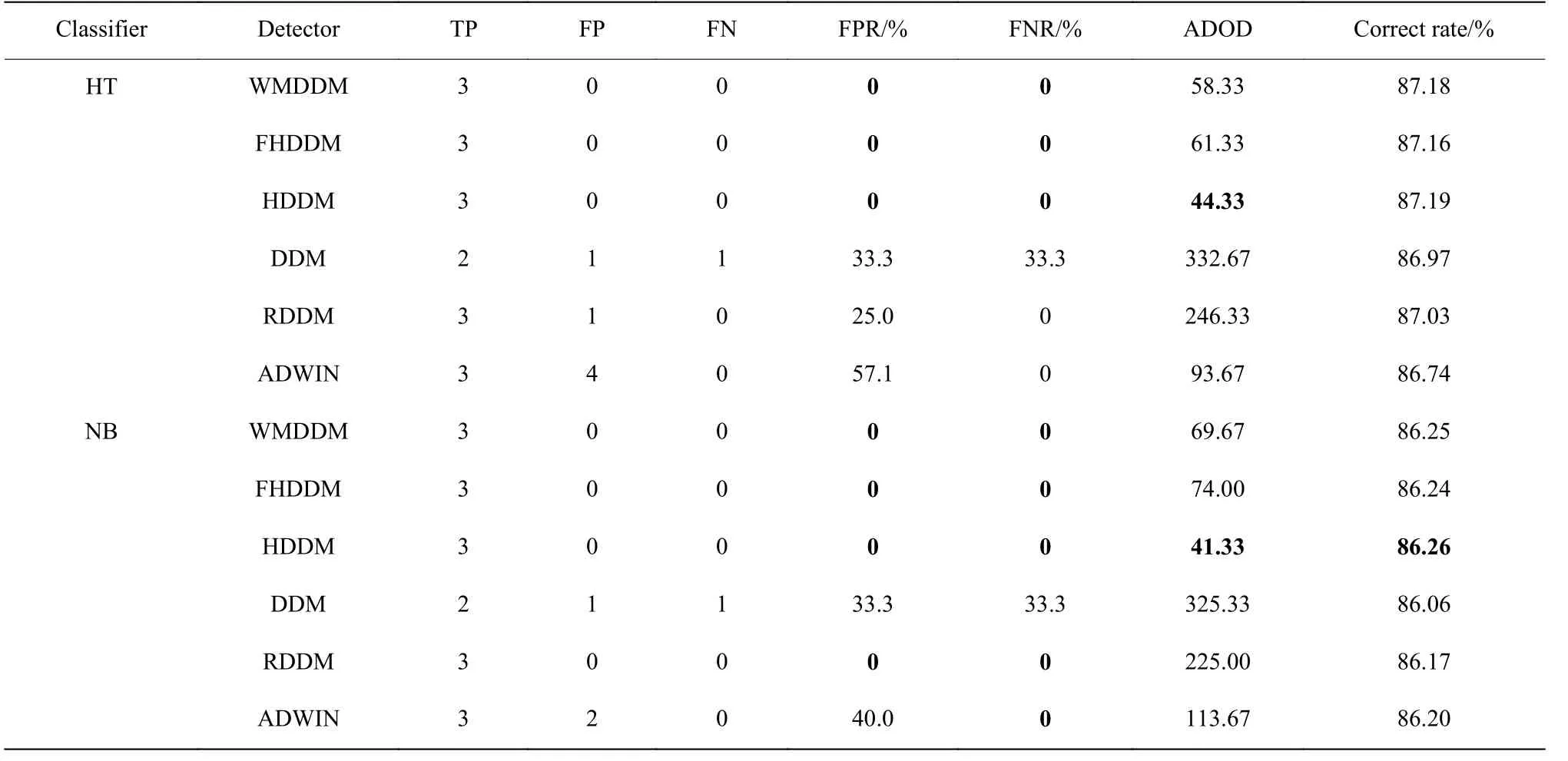
表7 CIRCLE 数据集上的实验结果Table 7 Experimental results on the CIRCLE dataset

图6 是HT-WMDDM、HT-FHDDM 和HT 在真实数据集Electricity 的分类准确率对比图，横坐标表示样本量，纵坐标表示分类正确率。由于真实数据集中概念漂移发生的位置和次数都是未知的，因此更能体现WMDDM 的泛化能力。由图6 可看出，HTFHDDM 和HT-WMDDM 的分类正确率高于HT，说明加入检测器能提升分类器的性能。HT-WMDDM 的分类正确率要高于HT-FHDDM。实验表明，WMDDM算法对于真实数据环境有较好的适应能力，具有较强的抗漂移能力。

图6 Electricity 数据集上的分类准确率对比图Fig.6 Comparison chart of classification accuracy on the Electricity dataset

通过上述对比实验，可以得出：第一，WMDDM算法的自适应加权机制具有自我调节能力，且具有较强的鲁棒性；第二，WMDDM 算法具有更低的误报率、漏报率和平均检测延迟，能够快速准确地检测到突变型和渐进型概念漂移；第三，WMDDM 算法具有较强的数据流适应能力，无论是人工数据集或是真实数据集，都能够快速适应数据变化，提高分类器的性能。

4 结束语

本文提出了一种基于McDiarmid 边界的自适应加权概念漂移检测方法WMDDM，它先对分类结果加权，求出漂移和警告的McDiarmid 边界，再通过分析加权错误率的变化幅度以判断当前数据流的状态，根据反馈信号自动调节衰减函数以降低过时数据影响，提升检测效率和分类准确率。通过人工和真实数据集上的实验结果表明，WMDDM 在平均检测延迟、误报率和分类准确率上都具有一定优势。

本文只考虑了突变型和渐进型概念漂移的问题，无法解决重现型概念漂移所带来的额外消耗，且所采用的数据集是类别平衡的，而现实中存在许多类别不平衡的问题。因此，下一步将考虑多分类器和类别不平衡问题，以扩大概念漂移检测器的适用范围。