基于分布式深度神经网络的双馈风机低压故障穿越研究

张哲源，顾幸生

（华东理工大学能源化工过程智能制造教育部重点实验室, 上海 200237）

双馈风机（DFIG）低压穿越技术的本质就是使双馈风机具有低压穿越的能力。根据严格的风电场并网运行准则，风电机组在故障期间必须保证不脱网持续运行，即具备低电压穿越的能力。双馈风机低压故障是指在电网高压侧电压突然跌落时，双馈风力机机端电压下降，其产生的直接影响是定子电流急剧上升，磁通下降，并通过定、转子之间的强耦合使转子电流升高，然后双馈电机转子功率剧增，进而导致与其相连的背靠背功率变频器功率越限。该故障会导致发电机转子侧变频器发生过流或过压保护而退出运行，最终导致风力机过速停车，产生大规模的风力发电机组与电网解列。此外，随着风电渗透率的逐步提高，风机故障对电网的冲击也会变得愈发严重。因此研究风机低压穿越技术，是为了能够更好地保障电网电压在突然跌落时风机的稳定不脱网运行。

目前，双馈风机低压穿越的控制策略主要分为两类：第1 类是加入前馈补偿的定向矢量控制[1]策略，它适用于较低程度的电压跌落；在严重电压跌落的情况下，仅通过定向矢量控制难以达到要求，因此引入了第2 类撬棒保护控制策略，这种控制策略保证了双馈风机的持续并网运行，为系统提供无功支撑，有利于系统恢复[2]。此外低压穿越还会受其他因素影响，如文献[3]就着重研究了双馈风机转子变流器控制系统中PI 参数的选择对机组低压穿越效果的影响。

为取得更好的控制性能，需选择较优的PI 参数。部分学者采用各种优化算法对PI 控制器参数kp、ki进行优化，包括蚁群算法[4]、遗传算法[5-6]、粒子群算法[7-8]及其他智能算法[9-10]。这类算法存在如下问题：在实际过程中，故障的持续时间通常不会太久，产生故障后再优化会由于算法本身消耗的时间使控制效果不理想，实用性较差。

为了提高算法的实用性，本文采用故障分类方法和智能优化算法结合的双馈风机的低压穿越控制策略。首先通过电磁暂态仿真软件PSCAD 搭建好双馈风机并网控制模型，对风机故障过程进行大规模仿真[11-13]，并根据对实际电网造成的损失程度来进行故障分类，构建不同故障等级下的参数优化策略；然后利用粒子群优化算法对不同策略下的控制参数进行离线优化，主要针对的是kpd、kid、kpq、kiq（分别表示d轴上的比例增益，q轴上的积分增益，q轴上的比例增益和q轴上的积分增益）这4 个控制参数和阈值hy。优化PI 参数能降低不同情况下转子电流的超调量和调节时间，提高转子侧变流器控制的稳定性。适度调整阈值hy能控制电流在理想范围内；此外，在需要投入撬棒的情况下，也需要根据不同故障程度选择适合的撬棒电阻；最后建立神经网络来识别故障等级，将仿真算例形成训练集，以故障信息作为训练样本的输入参数对故障程度进行分类训练。训练成功的网络即构成控制策略优选模块，只需输入所采集的故障信息即可实时选择并确定优化的控制策略和参数，从而解决了实际故障中控制的实时性问题[14]。

1 双馈风机低压穿越控制参数优化

通过串联电阻分压的方式模拟电网电压的对称三相电压跌落故障，并将故障程度分成3 级：重度故障(跌落至电网电压的20%～40%)、普通故障(跌落至电网电压的40%～70%)、轻微故障(跌落至电网电压的70%～99%)。不同故障程度采取不同低压穿越方式和PI 参数。本文通过粒子群优化算法(Partical Swarm Optimization，PSO)实现PI 参数的优化。仿真实验在MATLAB 平台下进行，双馈风机额定功率为500 MW，额定电压为13.8 kV，额定频率为60 Hz，定转子电阻分别为0.005 4、0.006 07 p.u.，定转子匝数比为2.637，定转子漏感分别为0.102.、0.11 p.u.，励磁电感为4.362 p.u.。

1.1 控制策略框架

定子侧变流器采用双闭环控制，电压外环控制直流母线电压，直流电压给定值与反馈值的偏差经过调节器来决定有功功率的大小和方向。功率的大小反映在电流上，因此电流内环按照电压外环输出的功率进行电流控制。

转子侧变流器采用的是基于PI 环路的控制框架。其中外部控制回路通过调节发电机转子速度和无功功率以获得d、q轴转子电流基准和，内部控制回路通过和转换得到ira_ref、irb_ref和irc_ref，并与转子侧电流ira、irb和irc进行比较，用反馈型脉宽调制(Current Reference Pulse Width Modulation，CRPWM)的方式完成调制。这种框架利用外环的PI 回路与电流CRPWM 互相作用进行反馈调节，并利用PSO 进行参数优化以实现最佳控制性能[15]。

1.2 低压穿越策略

在不同的故障程度下选择不同的控制策略达到较好的控制效果。本文只考虑转子侧变流器的控制优化，控制框图如图1 所示，其中Qs和分别表示无功功率的实际值及其设定参考值，i表示电流，w表示离子转速。

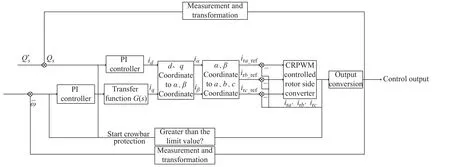
图1 转子侧变流器控制框图Fig.1 Control block diagram of rotor side converter

1.2.1 轻微故障控制策略 该控制策略中，优化参数为kpd、kid、kpq、kiq以及CRPWM 参数hy。其中，CRPWM 在所需电流参考波形周围放置上下公差带，允许在一定负载中产生任意电流波形。如果实际电流低于下阈值，则打开向负载施加正电压的上开关，电源中的电流随着该电压的升高而升高；当电流高于上限阈值时，上限开关断开，下限开关接通，并向负载施加负电压，使电流下降。因此，期望电流和实际电流之间的差异始终保持在公差范围内。通过减小阈值hy大小，可控制所需电流近似到任何必要的程度。当然阈值hy是有限制的，阈值越小，开关周期越小，即开关频率和损耗越高。综上所述，阈值hy的选择也十分重要。

优化目标为降低转子电流幅值和减小暂态直流分量，由此确定的相关公式和适应度函数为：

其中：Q是无功功率，uqs是定子侧q轴电压，ids是定子侧d轴电流，Ls是定子侧电感，iqs是定子侧q轴电流，Lm是定转子侧互感，iqr、是转子侧q轴电流的实际值和设定参考值，idr、分别是转子侧d轴电流的实际值和设定参考值，Ψ1为定子磁链。

根据要求，两个相互作用的PI 环路的参数需要被最优调节。外部控制回路中比例增益和积分增益kpd、kid、kpq、kiq在[0,1]、[0, 25]、[0,1 250]、[0,5]之间是有界的；内部控制回路中阈值hy在[0, 10]范围内变化，t是总操作时间，风速W限制在0～1.1 p.u.，电网电压限制在0.2～1.0 p.u.，无功功率限制在-100～200 kW。

由于d、q轴电流环结构相同，PI 参数设置相差不大，通过Z-N 整定法计算和多次仿真调整后得到其初始值，并在此基础上实现参数优化。

1.2.2 严重故障控制策略 严重故障下，由于受DFIG 变流器容量约束，故仅通过调整转子侧变流器PI 参数的控制策略难以发挥作用，需根据故障情况投入不同的撬棒电阻实现低电压穿越。可变电阻撬棒电路拓扑结构如图2 所示，其中DEA、DEB、DEC、DED、DEE 和DEF 代表6 个绝缘栅双极型晶体管（IGBT）。

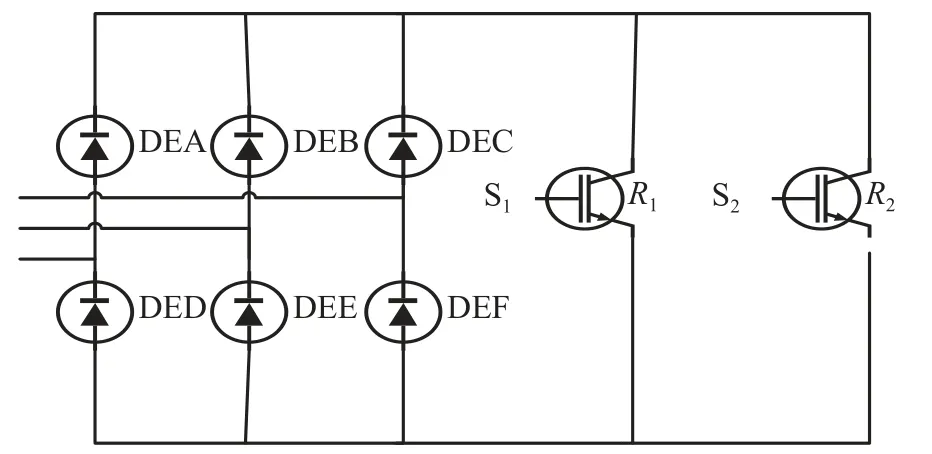
图2 撬棒保护电路Fig.2 Crowbar protection circuit

通过改变两个IGBT 开关（S1和S2）占空比（W1，W2）以及导通时的IGBT 阻值（R1、R2)控制撬棒等效阻值（Rc）的大小，计算公式为：

撬棒保护参数优化通过改变IGBT 导通时间和导通电阻来实时修改撬棒阻值。优化的目标是让无功功率输出稳定，并保证转子电流在故障时变化幅度降低，同时在满足直流母线电压Udc低于阈值的情况下尽可能减小超调。综上所述，适应度函数定义为：

其中：Udc和分别指直流母线电压的实际值和设定参考值。

1.2.3 普通故障控制策略 普通故障下，仅通过优化转子侧变流器PI 参数抑制转子电流的效果较差，不能满足控制要求，不利于风机的故障恢复；相对而言，仅靠纯撬棒保护虽然能有效抑制过电流和过电压，但投入撬棒保护会产生较多的无功消耗，且在撬棒阻值的选择上也有一定的要求。综上所述，通过采取撬棒保护和参数调节相结合的方式，能够有效解决两种方案单独投入时存在的弊端。在转子侧过电流严重时投入撬棒电路，切出转子侧变流器，当电流恢复到使用PI 控制的可控范围内再切出撬棒电路，采用变流器控制至故障结束。本文通过判断转子电流超限值来判断是否采用撬棒电路。

1.3 实验结果

通过PSCAD 仿真改变网侧串联电阻的方式模拟DFIG 低电压穿越暂态过程，当t=8.5 s 时，电网发生三相短路故障，8.7 s 时故障切除，然后通过软件接口将数据传入MATLAB 仿真粒子群优化过程，寻找最优参数。优化的种群规模100，迭代终止条件为迭代40 次。

1.3.1 轻微故障控制策略 优化前后参数对比如表1所示。

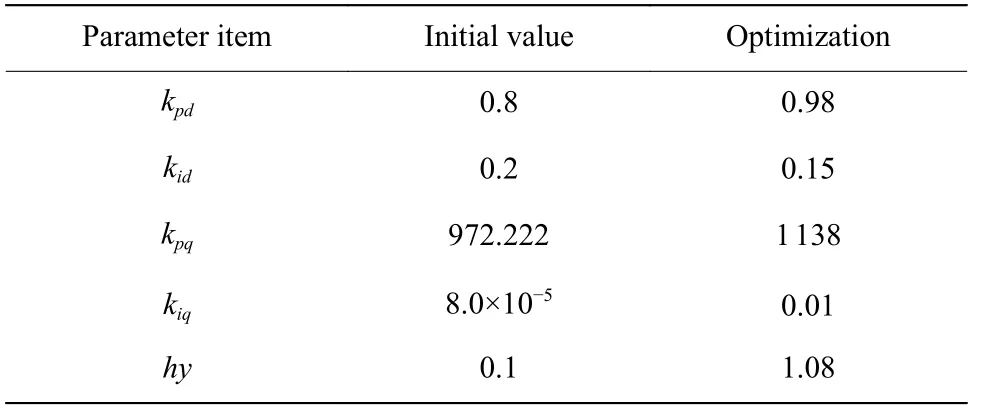
表1 控制器参数对比Table 1 Controller parameter comparison

图3 所示为传统控制和优化参数改进控制两种方案的仿真结果。对比发现，在参数优化后的控制中，转子电流峰值（ir）、电磁转矩（Te）和无功功率（Q）的波动幅度均较优化前更小，输出无功更稳定。

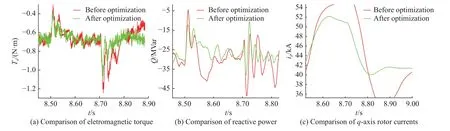
图3 电压跌落30%以内低压穿越特性对比Fig.3 Comparison of low voltage ride through characteristics within 30% voltage drop

1.3.2 严重故障控制策略 严重故障下电压跌落至20%～40%，当故障电流大于正常转子电流的1.5 倍时启动撬棒电路，并在撬棒电路启动后停止原本的调制手段。固定撬棒电阻和可变电阻两种方案的参数选择如表2 所示，仿真结果如图4 所示。

表2 优化前后撬棒电阻Table 2 Crowbar resistance before and after optimization

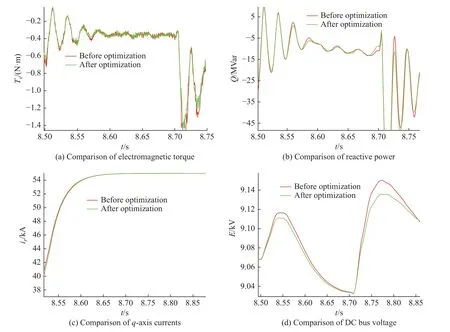
图4 电压跌落至32%时低压穿越特性对比Fig.4 Comparison of low voltage ride through characteristics when the voltage drops to 32%

分析可知，传统撬棒固定整定值相对较大，且在不同跌落程度下撬棒保护阻值固定。阻值优化后一定程度上缓解了转子过电流和直流母线电压过压的情况。如图4 所示，两种方案的电磁转矩和无功功率差异不大，但优化前的固定电阻方案波动大，对机组安全更为不利，并且可以看到优化后降低了直流母线电压（E）的超调量，达到了预期效果。

1.3.3 普通故障控制策略 当电压跌落至45%时，对外环PI 控制器、CRPWM 参数hy和撬棒等效阻值（Rc）进行优化，采取的策略为：当故障电流低于转子正常电流的1.25 倍时，采用轻微故障策略的控制方式；在故障电流超过转子正常电流的1.25 倍后，采用严重故障策略的控制方式。参数如表3 所示。

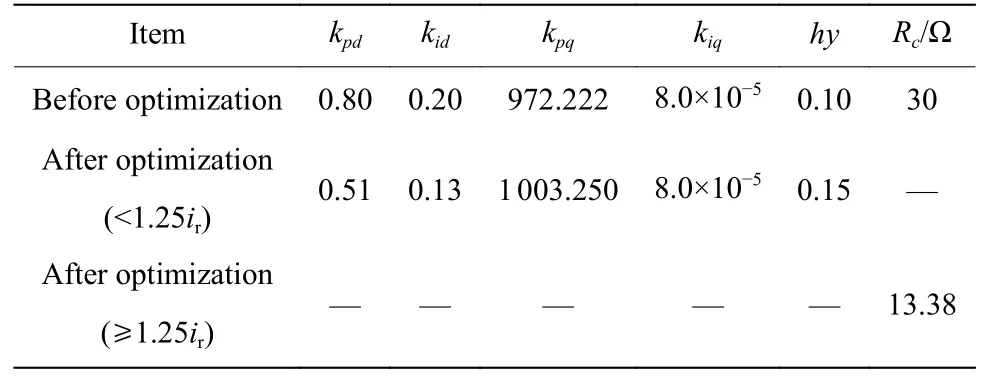
表3 优化前后控制参数对比Table 3 Comparison of control parameters before and after optimization

图5 所示为在电压跌落至45%时3 种方案的低压穿越特性对比。其中，联合控制的电流门槛值设为正常转子电流的1.25 倍，故障情况下当转子电流高于常态的1.25 倍时，启动撬棒电流抑制转子过电流；当转子电流低于常态的1.25 倍时，采用优化控制参数的变流器控制方式。这种控制策略能减少撬棒电阻投入的时间和次数，在抑制转子过电流方面有较好的效果。在联合控制策略下，无功功率和电磁转矩的控制效果均介于两种单独控制之间，直流母线电压超调量也相对减小，风机机组更加稳定。这种二者结合的控制策略能有效继承单独控制的优点，因此适用于中度的电压跌落情况。

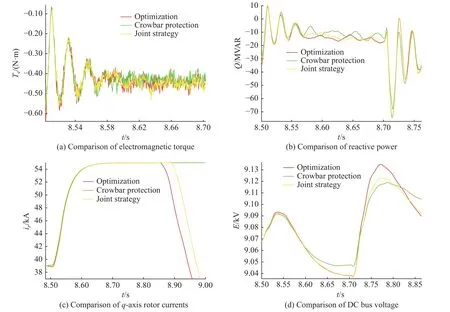
图5 电压跌落至45%时低压穿越特性对比Fig.5 Comparison of low voltage ride through characteristics when the voltage drops to 45%

综上所述，不同故障程度都有对应的低压穿越策略：轻微故障采用优化参数的控制策略；中度故障采用联合控制策略；严重故障采用单独投入撬棒电路的控制策略。

2 故障程度识别模型

2.1 数据预处理与分布式深度神经网络（DNN）故障模型训练

2.1.1 故障特征选择 为了在不对故障识别准确率造成较大影响的情况下适当缩减训练时间，本文利用PCA 主成分提取的思想[16-18]，合理选择特征较为明显的数据，归并特征不明显的数据。通过正常工况下的数据平均值与不同故障程度下的数据平均值的相差程度、故障数据与正常数据的离散程度来选择特征明显的数据，并将特征不明显的数据按照一定比例加权合成，最终达到降维的效果。相关公式如式（5）～式（7）所示：

其中：s1i、s1k表示特征i和特征k与故障的关联程度，表示特征i的数据在正常状态下的平均值，表示特征i的数据在故障状态下的平均值，s2i表示特征i与正常数据的离散程度，xkun表示各个故障数据点，Nsyn表示加权合成的特征，ωi为待合成特征i的权重值，Xi为特征i的数据值，m为特征项总数。

2.1.2 训练样本选择 神经网络训练的时间和准确度不仅与网络参数、隐藏层神经元个数和隐藏层数量等因素相关，它还与训练样本的多少以及训练样本的选择有关。本文采用欧氏距离和Person 相关系数来进一步提取有效的训练样本。

欧氏距离用来计算两个向量间的自然长度，公式如下：

其中：re代表第n维向量xin与xjn的欧氏距离，xi及xj表示不同数据点，m是向量的维度。

Person 相关系数衡量的是线性相关关系。若相关系数为0，只能说x与y之间无线性相关关系，不能说无相关关系。相关系数的绝对值越大，相关性越强，即相关系数越接近于1 或-1，相关度越强；相关系数越接近于0，相关度越弱。公式如下：

其中：rPer代表第n维向量xin与xjn的Person 相关系数，表示平均值。

按照式（8）和式（9）分别计算训练数据的欧氏距离和Person 相关系数，分别取欧式距离为最小值的数据和Person 相关系数接近1 的数据作为神经网络的训练数据[19]。

2.1.3 分布式DNN 训练 DNN 本质上是包含多个隐含层的前馈神经网络，也是近年来发展迅速的深度学习网络的一种。DNN 具有很好的非线性映射关系和学习能力，适宜处理更大的函数集合[20-22]，结构如图6 所示。

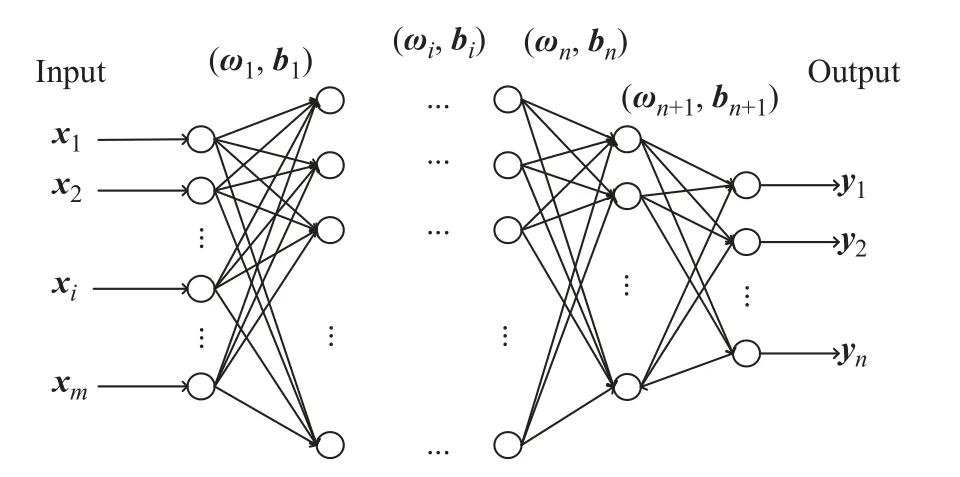
图6 DNN 结构图Fig.6 DNN structure diagram

图6 所示的x1,x2,···,xm为模型输入，是由故障信息中提取的定、转子电压电流等数据所组成的向量。DNN 输入层采用线性恒等函数作为激活函数，隐含层层数为n，最终传递给网络的输出向量为y1,y2,···,yn。(ωi,bi) 分别为第i个隐含层的权重矩阵与偏置。假定第i-1 隐含层的输入向量为

则第i层神经元的输出向量a(i)可表示为：

其中：α(i)为第i层神经元数目，ωi-1、bi-1分别为第i-1层的权重矩阵和偏置。隐藏层传递函数f(x)采用Tansig 函数，输出层传递函数采用Purelin函数，反向传播的训练函数采用Trainlm 函数。

首先，通过反向传播训练函数、训练集和训练集标签训练得到DNN 故障识别模型。然后，通过隐藏层函数和输出层函数计算测试集，获得一维的故障等级，并与实际的故障等级比较，输出DNN 网络故障预测的准确率。最后，由式(12)可求得整个网络输出为：

其中：最后一层隐含层神经元数量为β，fn为计算的最后一层隐含层输出，ωn+1、bn+1分别为输出层权重矩阵和偏置。

采用图7 所示的分布式DNN 训练流程获得各个子分类器。由于子分类器的训练样本是随机抽样获取，且子分类器参数也互不相同，导致识别出的故障等级也会有一定差异。首先利用该方法进行数据预处理，提取特征较为明显的数据；然后通过Person系数和欧氏距离法减少数据的冗余程度，降低神经网络训练的复杂度，提高了效率；最后采用分布式训练方法，遵循少数服从多数的原则，使模型预测的结果有了更好的准确度。

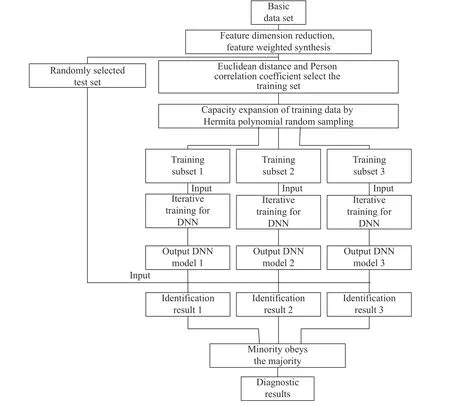
图7 分布式DNN 训练流程图Fig.7 Distributed DNN training flow chart

2.2 仿真结果

为方便研究，本文仅考虑了三相短路故障的情况。为了仿真不同程度故障下DFIG 的故障暂态过程，需选取故障发生前后DFIG 的定子电压、定子电流、转子电流、直流母线电压、无功功率等共12 维数据作为DNN 的训练集和测试集进行故障识别。由于需要3 个子分类器，本文采用3 次Hermita 多项式差值方式对原始训练数据进行扩容。

根据实际要求更改电网电压分压电阻大小来满足不同程度的故障跌落要求，并选择6 000 个正常数据点和6 400 个故障数据点，共12 400×12 维数据作为原始训练数据。故障仿真训练集和测试集参数表分别如表4 和表5 所示。

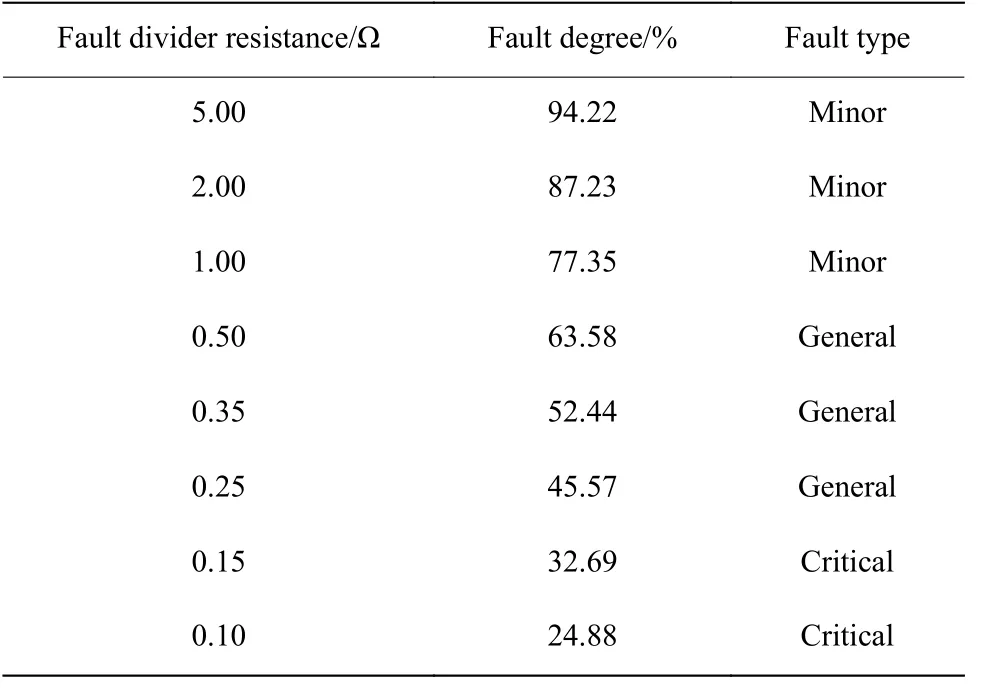
表4 故障仿真训练集参数表Table 4 Parameter table of fault simulation training set

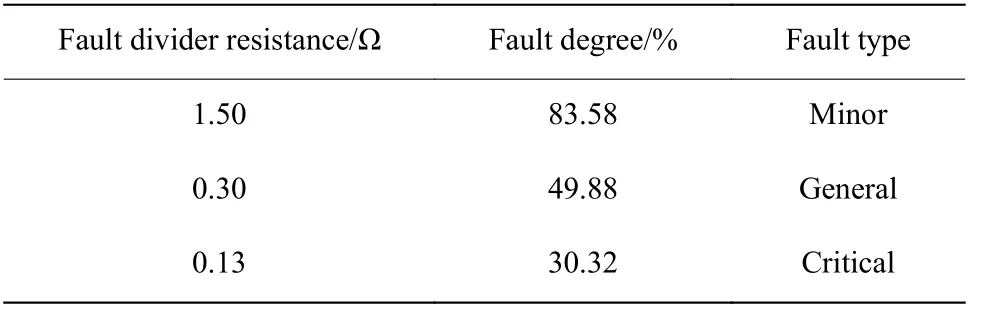
表5 故障仿真测试集参数表Table 5 Parameter table of fault simulation test set

通过改变故障分压的电阻模拟与风机并网点的不同距离处产生故障的情况，选取8 个故障点反映故障位置与电网的远、中、近距离，并与故障程度以及电压跌落幅度相对应。根据电压跌落程度将故障类型设为轻微(故障1)、普通(故障2)和严重(故障3)3 种，DNN 的标签即为相应故障类型下的优化控制参数。

DNN 的训练时间和分类效果不仅受训练集和测试集数据的影响，还受网络参数的影响。目前已经被证明的有DNN 的隐含层层数、各层神经元个数、迭代次数等均会影响训练的精度和时间。其中，隐含层的层数越多，越能有效识别特征，获得更好的分类效果；学习率过大，会出现训练震荡的问题，使达到相同测试准确率的时间变长；在隐含层层数相同、迭代次数相同的情况下，神经元数量增加能提升准确率，但是数量太多容易出现过拟合现象；训练的迭代次数越多准确率越高。

在确定上述参数的前提下，将本文故障识别方法与目前用于双馈风机故障识别的方法（传统DNN 和BP 神经网络）进行对比，表6 给出了策略1(文献[14]中的传统DNN 故障识别)、策略2（传统BP 神经网络故障识别）、策略3(数据预处理DNN 故障识别)以及策略4(分布式DNN 故障识别)的测试结果。

表6 不同策略下DNN 故障识别仿真结果Table 6 Simulation results of DNN fault identification under different strategies

分析表6 可知，文献14 采用原始数据DNN故障识别方法（策略1），因为风机模型不同，获取数据有差别，所以复用其方法对本模型数据进行故障识别，并在此基础上进行对比实验（策略3 和策略4）。策略2 用BP 神经网络进行故障识别，由于BP 神经网络结构简单、隐藏层单一，其故障识别速度相比于多层深度神经网络要快很多，但精确度较低。由以上分析可知，传统的BP 神经网络虽然速度较快，但精确度最低，故这里仅做参考。而文献[14]中的DNN将所有数据进行训练，准确度虽有明显提升，但速度大幅下降。在此基础上进行了数据特征提取(策略3)后，测试准确度下降了1.17%，而平均训练时间提升了664 s，即训练时间降低了29.6%。相比于前3 种训练方式，分布式DNN 测试(策略4)由于其分布式训练、投票选择的特点，能在提高训练时间的同时，几乎不降低其测试准确率，达到了实验的预期效果，足以证明改进有效。

3 结束语

电网电压跌落故障的发生通常有时间随机、影响较大的特点，且风电机组低压穿越期间不脱网运行的时间与电网恢复时间相对应，所以要求风机能够保证在一定时间内不脱网持续运行。传统控制方式在时效性上无法满足低压穿越的控制要求。为了能够根据电网故障的程度及时选择不同低压穿越策略，达到更好的控制效果，本文采用离线参数优化和故障模型训练、在线故障识别的方式，在发生故障后快速准确识别出故障类型，选择合适的控制策略和优化参数，一定程度上避免了复杂在线计算和风机大面积脱网的情况，提升了双馈风机低压穿越时的控制效果。