贮存老化对某弹药射程的影响研究
杜永强,王磊,胡江,高龙
贮存老化对某弹药射程的影响研究
杜永强,王磊,胡江,高龙
(海军大连舰艇学院,辽宁 大连 116000)
研究长期贮存老化对某弹药射程的影响,确定其有效增程射角范围。对130 mm某弹药在不同贮存老化时间下的射程进行数值仿真分析,揭示其射程和有效增程射角范围随贮存时间的变化规律。结合射程与贮存老化时间和射角之间的函数关系,提出以剩余推力比为表征参数的射程变化模型。在相同贮存老化时间下,随着射角的增大,该弹药的射程呈现出先增大、后减小的趋势。相同射角下,射程随贮存老化时间呈线性下降趋势,有效增程射角范围逐渐减小。使用三次多项式拟合有效增程比与射角之间的函数关系,拟合方程的相关系数超过了0.997 0。该弹药射程变化模型的拟合结果与仿真计算结果的相关系数大于0.998 5,表明其可以准确描述该弹药的射程变化规律。贮存老化会显著影响某弹药的射程和有效增程射角范围,在实际贮存和使用过程中,不能忽略其贮存老化因素。
贮存老化;射角;射程;剩余推力比
某弹药通过在弹丸底部加装发动机,借助发动机点火产生的推力实现弹丸的二次增速,能够达到增程25%~50%的目的[1-2]。复合固体推进剂作为发动机的动力源,也是该弹药长期贮存过程中的薄弱环节,在长期贮存期间会发生老化[3-4],即使未达到报废年限,也会导致发动机的推力下降,缩短弹药的射程,影响作战效能的正常发挥。因此,亟需揭示该弹药的射程变化规律,并准确预估其在不同贮存老化时间下的有效增程射角范围。
该弹药的射程主要受射角、发动机点火时刻以及助推时间等因素的影响[5]。Arkhipov等[6]研究了延迟点火对射程的影响,通过优化弹药的结构设计,探索了发动机点火的最佳延迟时间。刘鹏等[7]研究发现,发动机点火时刻的精度会影响弹丸射程的散布,二者近似呈线性关系。高佳驰等[8]研究表明,发动机点火时刻对弹药增程比的影响较大,在其他条件不变的情况下,通过调整点火时刻能够改变约30%的射程。相比于点火时刻,发动机助推时间对射程的影响不超过5%。该弹药作为“长期贮存,一次使用”的作战武器装备[9-10],若忽略了贮存老化对其增程比的影响,会显著降低其射击精度,阻碍作战效能的可靠发挥。
徐学文等[11]研究发现,随着发动机贮存时间的延长,推进剂中被氧化的铝粉成分逐渐增多,导致推进剂的燃速整体呈现下降趋势。燃速的下降会进一步降低发动机所能提供的推力值。解红雨等[12]同样得出,发动机经过贮存老化后,推进剂的燃速降低,发动机的压强和推力均减小,内弹道性能逐渐下降,且贮存老化时间越长,燃速下降得越明显,对内弹道性能的影响也越显著。在唐庆明等[13]的研究中表明,实际贮存过程中,复合固体推进剂受到老化作用的影响,其宏微观性能会发生劣化,微观上表现为推进剂内部发生了氧化交联等不可逆反应,宏观上表现为能量的损失,推进剂所能提供的推力逐年下降。研究发现,相比于刚出厂时发动机所能提供的推力,贮存14 a后,发动机所能提供的推力下降了30.3%。以推力为失效判据,预估复合固体推进剂的贮存寿命在18 a左右。目前国内外公开发表的文献当中,关于贮存老化对弹药射程影响的研究成果还较少。若要准确验证贮存老化对弹药射程的影响,需要结合自然环境贮存老化试验[14-15]和动态射击试验[16],但这种方法费用高、耗时长、难度大、危险性高,通常采取模拟仿真的方法替代部分试验环节[17-18]。
本文采用数值仿真方法对不同贮存老化时间下某弹药的射程进行了计算分析,揭示了射程的变化规律,分析了贮存老化对有效增程比的影响。通过构建射程与射角、贮存老化时间的函数关系,提出了以剩余推力比为表征参数的射程变化模型。研究结果可为相关研制部门和一线作战使用单位提供参考。
1 模型和方法
1.1 外弹道特征
该弹药的外弹道可以划分为3个阶段,如图1所示。
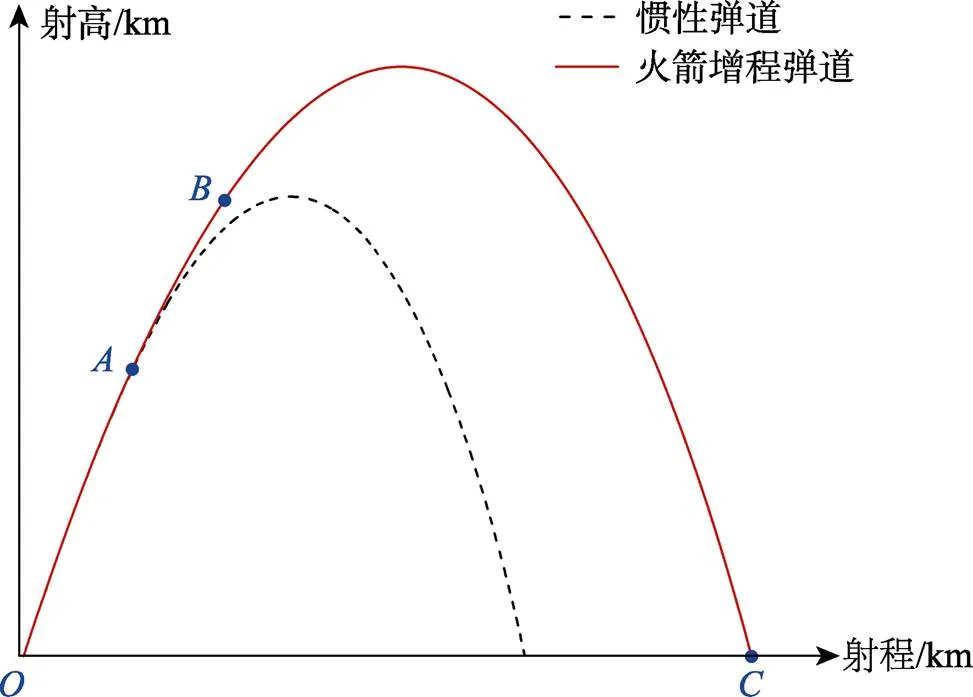
图1 弹道与惯性弹道曲线
惯性运动段Ⅰ(段):弹丸出炮口(点)后,在空气动力和重力作用下做惯性运动,其弹道特征与未增程弹丸的惯性弹道相同。此时,发动机尚未工作,这主要是由于在炮口处扰动较大,弹丸受到空气动力的影响,其阻力加速度达到最大值。若进行助推,会增大横向散布,同时耗费助推能量,减弱增程效果[19-20]。因此,在这一阶段,弹丸并未受到发动机的推力作用。
助推段(段):进入助推段后,发动机点火(点为点火时刻),弹丸除受到空气动力和重力外,还受到推力的作用进行二次增速,弹道曲线明显高于惯性弹道。由于弹药中复合固体推进剂燃烧速度较快,因而助推段持续时间较短,通常在2 s左右。到达点时,发动机停止工作,助推段结束。
惯性运动段Ⅱ(段):与段相同,弹丸受到空气动力和重力作用做惯性运动,直至弹丸落地(点)。由于增加了助推段,弹丸的最大射高和射程明显大于惯性弹道,表明能够通过助推的方式实现传统炮弹增程的目的。
1.2 基本假设
本文重点研究贮存老化对弹药增程比的影响,不涉及弹丸的控制过程,因而采用相对简单的质点外弹道模型[21],略去对弹丸运动影响较小的力和力矩,揭示弹丸在重力、空气动力和发动机推力作用下的运动规律。为便于后续计算分析,根据经典外弹道理论[22],作出以下基本假设:弹丸为轴对称,且章动角为0;地表为平面,重力加速度保持9.80 m/s2不变,且方向始终铅直向下;科氏加速度为0;气象条件为标准无风雨;发动机开始工作(图1中点)和停止工作(图1中点)时提供的推力按阶跃函数处理,视为瞬间变化;发动机工作过程(图1中段)中,推进剂的质量保持不变,其提供的推力视为恒定值,且推力方向与弹丸速度方向保持一致。
1.3 质点弹道模型
根据1.2节中的基本假设,设弹丸质心的坐标为(,),采用以时间为自变量的自然坐标系,建立该弹药的质点弹道方程组。坐标原点位于弹丸质心,切线方向沿速度矢量方向,与速度矢量方向相同为正,法线方向与切线方向垂直,向上为正。
1)惯性运动段Ⅰ和惯性运动段Ⅱ:
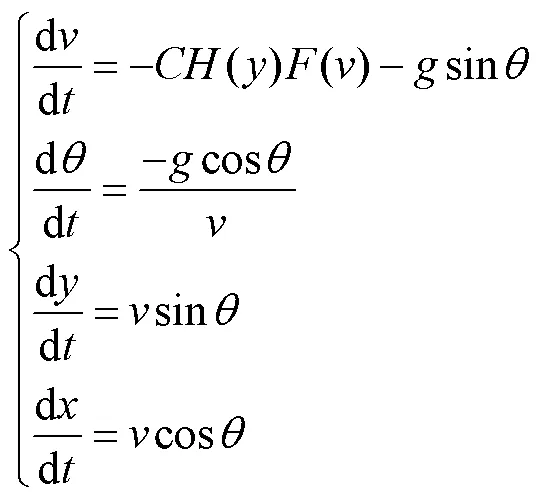
式中:为弹丸速度,m/s;为基于43年阻力定律的弹道系数;()为空气密度函数;()为阻力函数;为重力加速度,=9.80 m/s2;为弹道倾角,(°);为弹丸飞行高度,km;为弹丸飞行水平距离,km。
上述参数的计算见式(2)。

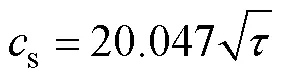
2)助推段:
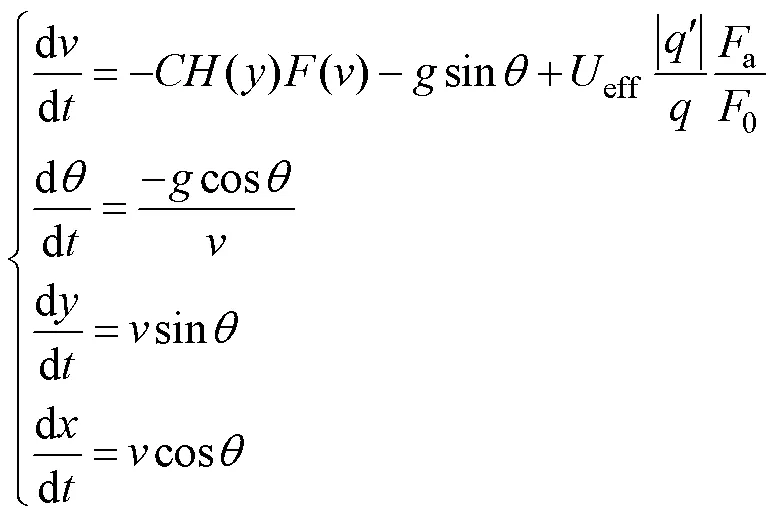
式中:eff为发动机有效排气速度,m/s;为弹丸质量变化速率,kg/s;a/0为贮存一定年限后发动机的剩余推力比,用以表征贮存老化对发动机推力的影响。其中,a为贮存某一年限后发动机能够提供的推力,N;0为未老化时发动机能够提供的推力,N。
助推段和惯性运动段Ⅰ、Ⅱ相比,主要区别在于在第一个方程中增加了助推部分,其余参数相同。
1.4 数值仿真计算方法
本文以某型130 mm弹药为例,借助MATLAB软件建立其数值仿真计算模型,利用四阶龙格库塔法[23-24]进行仿真计算分析,步长取0.01 s。为了研究贮存老化对该弹药射程的影响,发动机提供的实际推力变化规律参照文献[13],其余参与仿真计算的基本参数见表1。
求解火箭增程弹质点弹道方程组时,满足各段边界光滑连续条件,且惯性运动段Ⅰ的积分起始条件为:
=0时,==0,=v,=θ(4)
2 结果及分析
2.1 贮存老化对射程的影响
不同贮存老化时间下,未增程弹丸与增程弹射程随射角变化的仿真计算结果如图2所示。可以看出,相同贮存老化时间下,未增程弹丸与增程弹的射程随着射角的增大均呈现出先增大、后减小的趋势,符合外弹道特征,其中未增程弹丸最大的射程出现在52°射角左右,增程弹的最大射程出现在54°射角左右,略大于未增程弹丸最大射程对应的射角。这主要由于增程弹在助推的作用下,其外弹道射高和弹丸存速均高于同一飞行阶段的未增程弹丸,受到空气动力、重力和发动机推力的综合影响,为了达到最大射程,增程弹对应的射角略大于未增程弹丸。
表1 数值仿真计算基本参数

Tab.1 Basic parameters of numerical simulation calculation
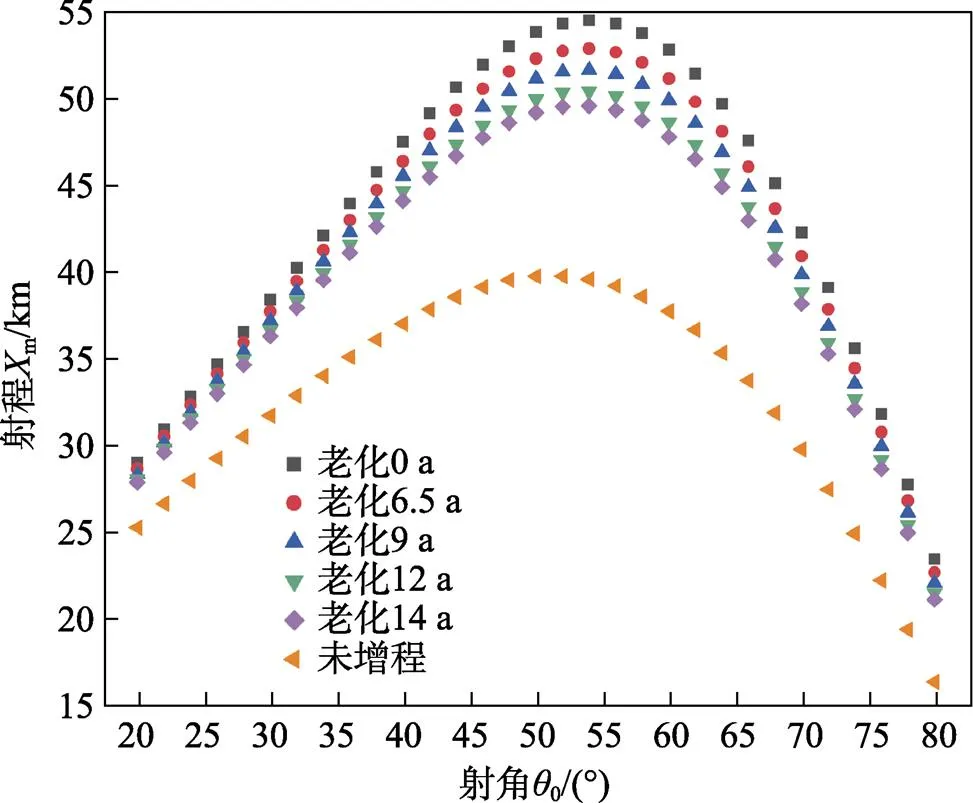
图2 未增程弹丸与增程弹射程随射角变化的仿真计算结果
相同射角下,增程弹的射程明显大于未增程弹丸,表明采用助推的方式能够可靠增大弹丸的射程。随着贮存老化时间的延长,增程弹的射程呈下降趋势,这主要是由于发动机中的复合固体推进剂在贮存期间发生老化[25-27]。老化时间越长,复合固体推进剂的性能劣化越严重,发动机点火时所能提供的推力下降得越明显,进而导致增程弹的射程缩短。
对不同射角下,增程弹射程随贮存老化的变化进行定量分析,结果如图3和4所示(以20°、30°、40°、50°、54°、60°、70°、80°为例,其余射角变化规律相同)。
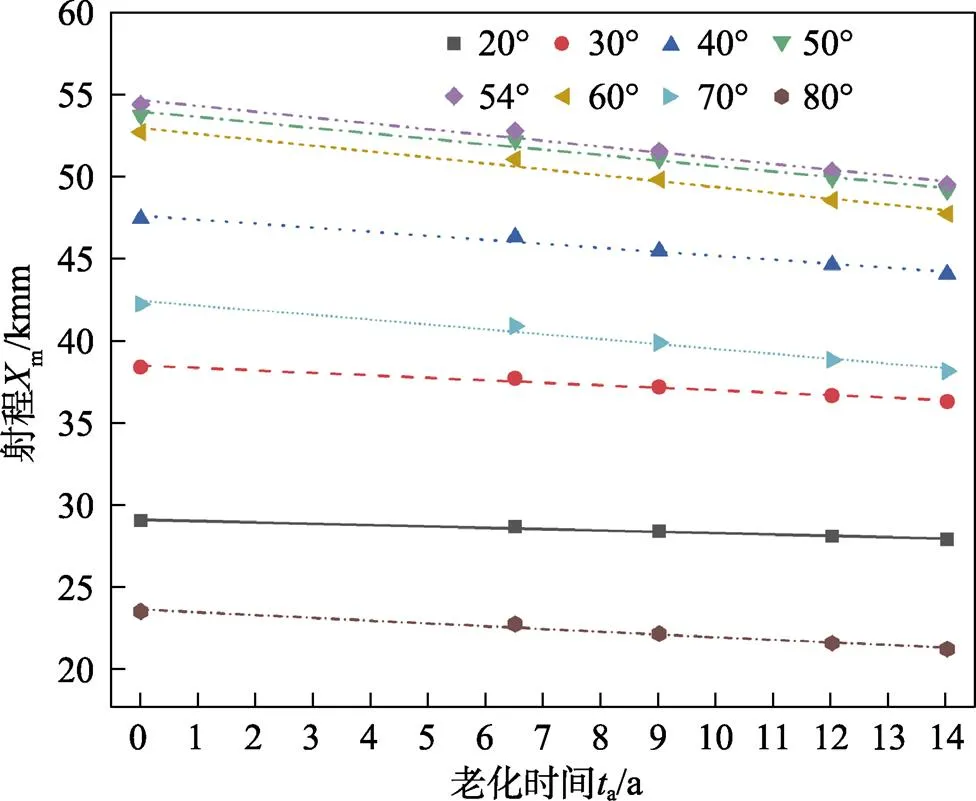
图3 射程随老化变化仿真结果和线性拟合曲线

图4 不同贮存老化时间的射程下降量
由图3和4中仿真结果和拟合曲线可以看出,任意射角下,增程弹的射程随贮存老化时间的延长均呈线性下降。相同贮存老化时间下,增程弹射程的下降量随射角呈现出先增大、后减小的趋势,与射程随射角的变化趋势相同,表明贮存老化对不同射角下的射程影响程度不同,射程越大,贮存老化的影响越明显,射程下降量越大。装备增程弹的目的之一是为了提高弹丸射程,增强远程作战能力[28],若忽略贮存老化的影响,会严重影响舰炮的射击精度,无法完成既定作战任务。
2.2 贮存老化对有效增程比的影响
以未增程弹丸的射程为基准,则增程弹的增程比可由式(5)计算得到:

式中:Xm0为某一射角下未增程弹丸的射程,km;Xma为同一射角下贮存一定年限的增程弹的射程,km。不同贮存老化时间下,增程弹的增程比随射角变化的仿真结果如图5所示。
由图5中可以看出,随着射角的增大,增程弹的增程比先快速增加、后缓慢增大,这主要是因为增程弹的射程随射角变化的同时,未增程弹丸的射程也在动态变化,两者的变化并不完全同步。同时,增程比越大,并不代表射程越大,如不同贮存老化时间下的最大射程为54°射角时,但此时增程比并不是最大值。
为了充分有效发挥增程弹的增程能力,在未增程弹丸能够达到的最大射程范围内,不需要直接采用增程弹完成射击任务,为此需要确定不同贮存老化时间下增程弹能够有效增程的射角范围。
以未增程弹丸的最大射程为基准,定义增程弹的有效增程比为:

式中:m0max为未增程弹丸的最大射程,km;ma为某一射角下贮存一定年限的增程弹的射程,km。
不同贮存老化时间下,增程弹有效增程比随射角的变化仿真结果如图6所示。
由图6中可以看出,在特定射角范围内,增程弹的有效增程比大于0,表明射程大于未增程弹丸的最大射程,此时采用增程弹能够有效发挥其增程能力。当射角过大或过小时,增程弹的有效增程比小于0,在此射角范围内射击,增程弹的射程虽然大于同一射角下的未增程弹丸,但小于未增程弹丸的最大射程,使用未增程弹丸同样能够完成射击任务,无法发挥增程弹的增程能力。另外,随着贮存老化时间的增加,增程弹有效增程比大于0所对应射角范围逐渐减小,这与贮存老化导致增程弹射程下降有关。
为了确定不同贮存老化时间下使用火箭助推增程的有效射角范围,同时为了避免计算过于复杂,使用三次多项式拟合有效增程比与射角之间的关系,设:

图6 有效增程比随射角变化仿真结果及拟合曲线

拟合曲线如图6所示,各参数拟合结果见表2。
由拟合结果可以看出,不同贮存老化时间下,有效增程比与射角拟合方程的相关系数均超过0.997 0,表明采用三次多项式可以准确描述有效增程比与射角之间的变化关系。根据建立的有效增程比与射角之间的三次多项式,得出不同贮存老化时间下使用火箭助推增程的有效射角范围,见表3。贮存老化6.5、9、12、14 a时,增程弹的有效增程射角范围分别减小了4.002 1%、8.018 9%、11.654 5%、14.263 1%。
表2 参数拟合结果

Tab.2 Fitting results of each parameter
表3 不同贮存老化时间下的有效增程射角范围

Tab.3 Range of effective extended range firing angle under different storage aging time
2.3 射程变化模型
2.3.1 模型的建立
由2.1节可知,增程弹的射程是射角和贮存老化时间的函数,参照有效增程比与射程函数关系的建立方法,设:
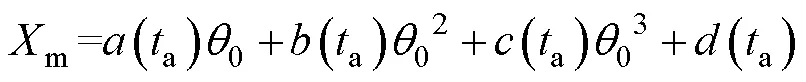
式中:(a)、(a)、(a)、(a)为与贮存老化时间相关的常数。
结合不同贮存老化时间下增程弹射程与射角的仿真结果,得到拟合曲线和参数拟合结果分别见图7和表4。
由拟合曲线和拟合结果可以看出,不同贮存老化时间下,增程弹射程与射角的拟合方程的相关系数均超过了0.997 0,表明采用三次多项式可以准确描述射程与射角之间的变化关系。
(a)、(a)、(a)、(a)为与贮存老化时间相关的常数,其与贮存老化时间之间的变化关系如图8所示。采用指数函数拟合模型参数与贮存老化时间之间的关系,指数函数也是常用的描述性能参数老化规律的模型[29-30]。拟合曲线如图8所示,拟合方程见式(9)。

图7 增程弹射程与射角模型拟合曲线
表4 射程变化模型参数拟合结果

Tab.4 Parameter fitting results of the range variation model

图8 模型参数与贮存时间变化关系及拟合曲线

结合式(8)和式(9),便得到以贮存老化时间为表征参数的增程弹射程变化模型。由于在实际贮存过程中,增程弹贮存老化的环境存在差异,以贮存老化时间作为表征参数存在一定的误差,模型的普适性不高,无法根据得到的射程变化模型准确预估贮存一定年限的增程弹射程变化情况,但以发动机的剩余推力比作为表征参数可以解决这一问题。
2.3.2 以剩余推力比为表征参数的射程变化模型
增程弹发动机剩余推力比随贮存老化时间变化关系如图9所示。在贮存老化过程中,增程弹的剩余推力比随贮存老化时间呈现先慢后快的降低趋势,近似呈指数变化规律。这主要是由于贮存老化前期复合固体推进剂各项性能较为稳定,受老化作用影响较小,推力的下降量不大。随着老化时间的延长,老化的影响占据主导地位,复合固体推进剂性能的劣化直接导致发动机推力的显著降低,因而到了贮存老化中后期,推力的下降量明显增大。
使用指数函数模型拟合剩余推力比与贮存老化时间的关系,得到:

指数函数模型的拟合相关系数大于0.990 0,表明可以使用指数函数模型准确描述剩余推力比与贮存老化时间的关系。对式(10)求反函数,即可用发动机剩余推力比表征贮存老化时间:

联立式(8)、式(9)和式(11),即可得到由剩余推力比表征的射程变化模型。
射程变化模型拟合结果与仿真结果相关关系如图10所示。可以看出,射程变化模型拟合结果能够准确描述仿真结果的变化规律,相关系数均大于0.998 5。在实际贮存过程中,根据发动机的剩余推力比,就能够对增程弹的射程进行预估。
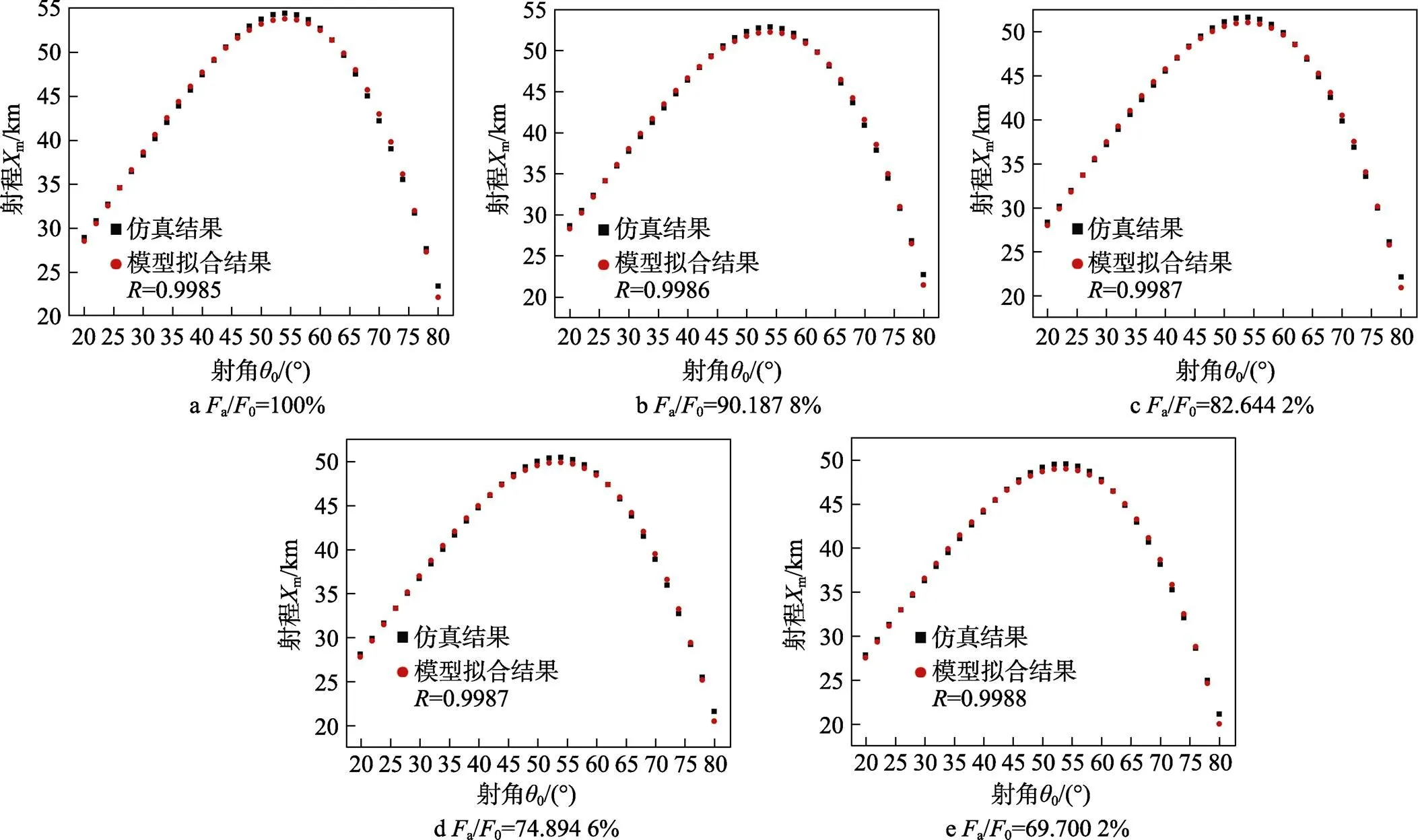
图10 射程变化模型拟合结果与仿真计算结果的相关关系
2.3.3 有效增程射角范围
设增程弹的有效增程射角范围为min(a)~max(a),根据表3中的有效增程射角范围,得到最小有效增程射角min(a)和最大有效增程射角max(a)随贮存老化时间的变化关系,如图11所示。

图11 θmin(ta)和θmax(ta)随贮存老化时间变化关系及拟合曲线
使用指数函数模型拟合二者之间的变化关系,拟合方程如式(12)所示。

拟合方程的相关系数分别为0.987 5和0.995 0,表明最小有效射程角和最大有效射程角与贮存老化时间之间满足指数变化关系。联立式(11)和式(12),即可得到以剩余推力比表征的有效增程射角,通过测定剩余推力比,就能够预估有效增程射角范围,为一线作战使用单位和相关研制部门提供理论支撑和参考依据。
3 结论
本文对不同贮存老化时间下某增程弹的射程进行了数值仿真分析,揭示了贮存老化对该增程弹射程和有效增程比的影响,提出了以剩余推力比为表征参数的射程变化模型。具体结论如下:
1)相同贮存老化时间下,射程随着射角的增大呈现出先增大、后减小的趋势,最大射程出现在54°射角左右,略大于未增程弹丸最大射程对应的射角。随着贮存老化时间的延长,该增程弹的射程呈线性下降趋势,这与发动机中的复合固体推进剂在贮存期间发生老化有关。
2)随着贮存老化时间的增加,该增程弹的有效增程比大于0,所对应射角范围逐渐减小。使用三次多项式拟合有效增程比与射角之间的函数关系,拟合方程的相关系数超过了0.997 0,并根据拟合方程得出了不同贮存老化时间下增程弹的有效助推射角范围。贮存老化6.5、9、12、14 a,有效增程射角范围分别减小了4.0021%、8.0189%、11.6545%、14.2631%。
3)结合射程与贮存老化时间和射角之间的变化规律,提出了以剩余推力比为表征参数的射程变化模型,给出了有效增程射角范围与剩余推力比之间的函数关系。射程变化模型拟合结果与仿真计算结果的相关系数大于0.998 5,研究结论可为一线部队作战使用和相关研制单位提供参考借鉴。
[1] SZKLARSKI A, GŁĘBOCKI R, JACEWICZ M. Impact Point Prediction Guidance Parametric Study for 155 mm Rocket Assisted Artillery Projectile with Lateral Thrusters[J]. Archive of Mechanical Engineering, 2020: 31-56.
[2] 李上文, 赵凤起, 罗阳, 等. 大口径炮弹增程技术对固体推进剂的要求[J]. 火炸药学报, 2003, 26(3): 20-23.LI Shang-wen, ZHAO Feng-qi, LUO Yang, et al. Requirements of the Extended Range Technology of Large Caliber Projectile for Solid Propellants[J]. Chinese Journal of Explosives & Propellants, 2003, 26(3): 20-23.
[3] 范志锋, 徐敬青, 崔平, 等. 超期服役炮射导弹增程发动机性能研究[J]. 弹箭与制导学报, 2016, 36(5): 81-84. FAN Zhi-feng, XU Jing-qing, CUI Ping, et al. Study on the Properties of Rocket-Assisted Engine of Gun-Launched Missile in the Extra-Service[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2016, 36(5): 81-84.
[4] WANG Zhe-jun, QIANG Hong-fu. Mechanical Properties of Thermal Aged HTPB Composite Solid Propellant under Confining Pressure[J]. Defence Technology, 2022, 18(4): 618-625.
[5] 钱建平, 李铁鹏, 宋成俊. 底排火箭复合增程弹射程影响因素及其规律性研究[J]. 弹箭与制导学报, 2006, 26(4): 129-131. QIAN Jian-ping, LI Tie-peng, SONG Cheng-jun. The Studies on the Influencing Factors and Regularity of Extended Range Effectiveness for Hybrid Base-Bleed-Rocket Extended-Range Projectile[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006, 26(4): 129-131.
[6] ARKHIPOV V, PERFILIEVA K. Optimization of Construction of the Rocket-Assisted Projectile[J]. MATEC Web of Conferences, 2017, 110: 01003.
[7] 刘鹏, 王雨时, 闻泉, 等. 火箭增程发动机点火时间精度对弹丸射程的影响[J]. 弹箭与制导学报, 2015, 35(5): 99-102, 106.LIU Peng, WANG Yu-shi, WEN Quan, et al. Effect of the Ignition Time Accuracy of Extended Range Rocket Engine on Projectile Range[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2015, 35(5): 99-102.
[8] 高佳驰, 王强. 火箭增程榴弹点火时刻与助推时间对射程的影响[J]. 弹箭与制导学报, 2020, 40(5): 87-90. GAO Jia-chi, WANG Qiang. Influence of Ignition Time and Boost Time of Rocket Motor on Range of Rocket-Assisted Extended Projectiles[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2020, 40(5): 87-90.
[9] ZHU Zong-peng. The Current Situation of China Manned Aerospace Technology and the Direction for Its Further Development[J]. Acta Astronautica, 2009, 65(3/4): 308-311.
[10] 董海平, 张静静, 魏小琴, 等. 温度交变条件下固体推进剂贮存寿命评估[J]. 北京理工大学学报, 2022, 42(5): 479-484. DONG Hai-ping, ZHANG Jing-jing, WEI Xiao-qin, et al. Storage Life Evaluation of Solid Propellant under Alternating Temperature Conditions[J]. Transactions of Beijing Institute of Technology, 2022, 42(5): 479-484.
[11] 徐学文, 辛庆伟, 倪保航, 等. 固体火箭发动机HTPB推进剂燃速性能老化研究[J]. 海军航空工程学院学报, 2015, 30(4): 349-352. XU Xue-wen, XIN Qing-wei, NI Bao-hang, et al. Research on Burning Rate Properties of HTPB Propellant in the Solid Rocket Motor[J]. Journal of Naval Aeronautical and Astronautical University, 2015, 30(4): 349-352.
[12] 解红雨, 吴勋, 成跃, 等. 高能推进剂老化对发动机内弹道性能的影响研究[J]. 装备环境工程, 2010, 7(2): 13-17. XIE Hong-yu, WU Xun, CHENG Yue, et al. Research on Influence of High Energy Propellant Aging on Interior Ballistic Performance of Solid Rocket Motor[J]. Equipment Environmental Engineering, 2010, 7(2): 13-17.
[13] 唐庆明, 裴哲, 吴建业. 固体火箭发动机的寿命研究[J]. 战术导弹技术, 2006(2): 30-32. TANG Qing-ming, PEI Zhe, WU Jian-ye. Research on the Life of Solid Rocket Engine[J]. Tactical Missile Technology, 2006(2): 30-32.
[14] ZHANG Ling-ke, ZHENG Xiang-yang. Experimental Study on Thermal Decomposition Kinetics of Natural Ageing AP/HTPB Base Bleed Composite Propellant[J]. Defence Technology, 2018, 14(5): 422-425.
[15] 丁彪, 张旭东, 刘著卿, 等. HTPB推进剂交变温度加速老化与自然贮存相关性[J]. 含能材料, 2011, 19(1): 50-54. DING Biao, ZHANG Xu-dong, LIU Zhu-qing, et al. Correlation between Alternating Temperature Accelerated Aging and Real World Storage of HTPB Propellant[J]. Chinese Journal of Energetic Materials, 2011, 19(1): 50-54.
[16] 李东. 固体推进剂药柱表面裂纹动态力学特性研究[D]. 南京: 南京理工大学, 2008. LI Dong. Dynamic Mechanics Characteristic Study of Surface Cracks in Solid Propellant Grain[D]. Nanjing: Nanjing University of Science and Technology, 2008.
[17] 石章松, 傅冰, 胡献君. 时间控制参数对增程修正弹射程影响仿真分析[J]. 电光与控制, 2013, 20(8): 11-13.SHI Zhang-song, FU Bing, HU Xian-jun. Influence of Time Control Parameters to Firing Range of Extended Range and Trajectory Correction Projectile[J]. Electronics Optics & Control, 2013, 20(8): 11-13.
[18] 张浩, 闻泉, 王雨时, 等. 炮弹地面密集度性能与射程关系仿真[J]. 弹道学报, 2016, 28(1): 56-59. ZHANG Hao, WEN Quan, WANG Yu-shi, et al. Simulation Research of Relationship between Ground Dispersion Performance of Projectiles and Firing Range[J]. Journal of Ballistics, 2016, 28(1): 56-59.
[19] 龙孝源. 增程弹固体火箭发动机“-”曲线的研究[J]. 兵工学报, 1983, 3(4): 75-81. LONG Xiao-yuan. Study on “-” Curve of Extended Range Projectile Solid Rocket Engine[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 1983, 3(4): 75-81.
[20] 欧阳福蕾, 李磊, 郭洪波, 等. 舰载制导火箭弹总体技术的若干问题探讨[J]. 战术导弹技术, 2021(1): 1-6. OUYANG Fu-lei, LI Lei, GUO Hong-bo, et al. Discussion on Several Issues of Shipborne Guided Rocket Overall Technology[J]. Tactical Missile Technology, 2021(1): 1-6.
[21] 徐明友. 火箭外弹道学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2004. XU Ming-you. Rocket External Ballistics[M]. Harbin: Harbin Institute of Technology Press, 2004.
[22] 韩子鹏. 弹箭外弹道学[M]. 北京: 北京理工大学出版社, 2014. HAN Zi-peng. Exterior Ballistics of Projectiles and Rockets[M]. Beijing: Beijing Institute of Technology Press, 2014.
[23] 朱磊, 陆欣. 固体发射药火炮身管热散失模拟研究[J]. 弹道学报, 2020, 32(3): 19-24. ZHU Lei, LU Xin. Simulation Study on Heat Dissipation of Barrel of Solid-Propellant Gun[J]. Journal of Ballistics, 2020, 32(3): 19-24.
[24] 董理赢, 焦志刚, 王志军, 等. 基于Matlab对弹丸外弹道运动轨迹仿真分析[J]. 兵器装备工程学报, 2017, 38(12): 98-101. DONG Li-ying, JIAO Zhi-gang, WANG Zhi-jun, et al. Simulation Analysis of Ballistic Trajectory of Projectile Based on Matlab[J]. Journal of Ordnance Equipment Engineering, 2017, 38(12): 98-101.
[25] DU Yong-qiang, ZHENG Jian, YU Gui-bo. Storage Life Prediction under Pre-Strained Thermally-Accelerated Aging of HTPB Coating Using the Change of Crosslinking Density[J]. Defence Technology, 2021, 17(4): 1387-1394.
[26] ADEL W M, LIANG Guo-zhu. Service Life Prediction of AP/Al/HTPB Solid Rocket Propellant with Consideration of Softening Aging Behavior[J]. Chinese Journal of Aeronautics, 2019, 32(2): 361-368.
[27] 于亮, 陈燕, 李智, 等. 复合固体推进剂老化研究[J]. 合成材料老化与应用, 2013, 42(5): 46-48. YU Liang, CHEN Yan, LI Zhi, et al. Summary of Study on Ageing of Composite Solid Propellant[J]. Synthetic Materials Aging and Application, 2013, 42(5): 46-48.
[28] 钟文超, 倪庆杰, 杨云川. 底排-火箭复合增程弹的外弹道参数设计[J]. 沈阳理工大学学报, 2008, 27(2): 58-61. ZHONG Wen-chao, NI Qing-jie, YANG Yun-chuan. The Design of the Exterior Trajectory Parameters of Bottom Exhaust-Rocket Compound Range-Extended Projectile[J]. Transactions of Shenyang Ligong University, 2008, 27(2): 58-61.
[29] QJ 2328—2005, 复合固体推进剂高温加速老化试验方法[S]. QJ 2328—2005, Test Method for Temperature Accelerated Aging of Composite Solid Propellant[S].
[30] 孔令泽, 董可海, 唐岩辉, 等. NEPE推进剂无损型贮存寿命预估[J]. 含能材料, 2022, 30(2): 163-170. KONG Ling-ze, DONG Ke-hai, TANG Yan-hui, et al. Non-Destructive Storage Life Prediction of NEPE Propellant[J]. Chinese Journal of Energetic Materials, 2022, 30(2): 163-170.
Effect of Storage Aging on the Range of Certain Projectile
DU Yong-qiang, WANG Lei, HU Jiang, GAO Long
(Dalian Naval Academy, Liaoning Dalian, 116000, China)
The work aims to study the effect of long-term storage aging on the range of certain projectile and determine the range of effective extended range firing angle. The range of a certain projectile used in 130 mm naval gun under different storage aging time was analyzed by numerical simulation and the variation law of range and the range of effective extended range firing angle with storage time were revealed. Combined with the functional relationship between range and storage aging time and firing angle of the projectile, a range variation model characterized by residual thrust ratio was proposed. The range of the projectile firstly increased and then decreased with the increase of the firing angle under the same storage aging time. At the same firing angle, the range decreased linearly with the storage aging time, and the range of the effective extended range firing angle decreased gradually. The cubic polynomial was used to fit the functional relationship between the effective extended range ratio and the firing angle, of which the correlation coefficient exceeded 0.997 0. The correlation coefficient between the fitting result of the range variation model and the range simulation calculation result of the projectile was greater than 0.998 5, which indicated that the range variation law could be accurately described by the proposed range aging model. Storage aging will significantly affect the range and the range of effective extended range firing angle of the projectile, which can not be ignored in the actual storage and use process.
storage aging; firing angle; range; residual thrust ratio
2022-12-04;
2023-01-19
DU Yong-qiang (1991-),Male, Doctor.
杜永强, 王磊, 胡江, 等.贮存老化对某弹药射程的影响研究[J]. 装备环境工程, 2023, 20(6): 018-027.
TJ450.1
A
1672-9242(2023)06-0018-10
10.7643/ issn.1672-9242.2023.06.003
2022–12–04;
2023–01–19
杜永强(1991—),男,博士。
DU Yong-qiang, WANG Lei, HU Jiang, et al.Effect of Storage Aging on the Range of Certain Projectile[J]. Equipment Environmental Engineering, 2023, 20(6): 018-027.
责任编辑:刘世忠

