基于多层线性模型的铝合金大气腐蚀规律研究

周俊炎，王竟成，杨小奎，王津梅，周堃，舒畅

基于多层线性模型的铝合金大气腐蚀规律研究

周俊炎，王竟成，杨小奎，王津梅，周堃，舒畅

（西南技术工程研究所，重庆 400039）

针对不同地区铝合金大气腐蚀差异性和样本数据利用不充分的问题，构建精度更高的铝合金大气腐蚀模型，研究铝合金在不同环境中的大气腐蚀规律。基于多层线性模型，构建具备层次结构的腐蚀率模型。以某型号铝合金腐蚀数据为研究对象，逐步建立零模型、随机系数回归模型、完整模型探究大气腐蚀规律，并进行预测评估。通过交叉验证进行模型评估，多层线性模型（MSE=0.001 3）优于幂函数回归（MSE=0.005 5），远优于线性回归（MSE=0.031 6），模型预测精度提升。多层线性模型能有效分解总方差，增强了模型的可解释性。多层线性模型有效结合铝合金腐蚀数据区域差异性特征，能表征大气腐蚀规律，具有一定的实用价值。

多层线性模型；铝合金；大气腐蚀；腐蚀模型；区域差异；可解释性

铝元素在地壳中含量丰富，铝及其合金被广泛应用于生活、运输等各大领域[1-2]。铝合金具有耐疲劳、低密度、高比强度、高比刚度和强耐蚀性等特点[3-4]，运用广泛，体量巨大，仅次于钢铁，对社会建设发展起支柱性作用。铝合金受大气环境影响[5-6]，易产生点蚀、剥层腐蚀、晶间腐蚀、应力腐蚀等腐蚀作用，严重影响产品的服役，甚至引发灾难性事故[7-8]。因此，研究铝合金大气腐蚀规律有助于制定防护措施，保障产品使用安全，具有显著经济效益和现实意义。

由于铝合金大气腐蚀环境试验存在样本量有限、时间跨度长、试验区域差异性大[9]等客观原因，导致试验数据体量小，具有区域性规律，难以构建基于大数据的模型算法。如神经网络[10]、混沌时序分析[11]等，数据驱动算法通过挖掘稀疏数据价值，搭建黑盒模型，但需要大体量数据支撑，在铝合金大气腐蚀规律研究中难以适用。

本文以某型号铝合金大气腐蚀数据为基础，应用多层线性模型进行规律研究，构建一个两层模型，分别探索不同地区环境因素带来的组间差距和时序变化带来的组内差异，更好地拟合试验区域，建立适应性更强、更贴合小样本的铝合金大气腐蚀模型，探究铝合金大气腐蚀规律。

1 多层线性模型

Lindley和Smith于1972年最早提出多层线性模型（Hierarchical Linear Model，HLM）[12]，其参数估计方法区别于传统回归分析方法，数据不必满足分布同质性和样本独立性假设，考虑多个层次的变量信息和随机误差，在处理层级数据具有优势，被广泛应用于社会[13]、教育[14]、人文[15]等各个领域。

多层线性模型基本公式见式（1）和式（2）。

(2)

第一层公式如（1）所示，Y是第个输出变量第组的实际值，代表试验组，代表第个实际变量；X是第一层相关的自变量；r是组内偏差的误差项。

第二层公式如（2）所示，形式与第一层公式基本相同，第一层随机效应参数β由第二层确定，在不同组别中取值不同。W是第二层相关的自变量，γ是关于W的固定效应系数，u是组间偏差的误差项。

多层线性模型适用于处理层级式、嵌套结构数据，一层数据通常由个体层面数据构成，高层次数据由个体层面共享的宏观通用数据构成。多层线性模型将高于个体层面的数据纳入回归模型，使单一随机误差分解到相应的多个水平层级上，改善拟合效果，同时利于进行分层级分析，系统研究不同层级变量对因变量的影响及交互作用[16]。

多层线性模型考虑了不同层次的随机误差和变量信息，能够提供更为准确的参数估计和假设检验。多层线性模型可以发现回归方程中的截距和斜率之间的相关关系，从而更好地解释自变量和因变量之间变化的规律，不仅可以通过回归得到宏观因子和微观因子对因变量的直接效应，还能通过水平回归方程与水平回归方程的结合，得到宏观因子对因变量与微观自变量关系的调节效应。

2 影响机理

国内外学者开展了大量铝合金腐蚀试验研究，罗来正等[17]开展了7050高强铝合金在我国4种典型大气环境下的腐蚀行为研究。赵全成等[18]开展了湿热海洋、干热沙漠7A85铝合金大气腐蚀研究。崔腾飞等[19]开展了于高强度铝合金在某工业海洋性气候地区加速试验方法研究。Arizmendi-Salgado等[20]开展了热处理与7075T6铝合金腐蚀行为研究。Melchers等[21]研究了铝合金大气腐蚀动力学和双参数模型。Vincken等[22]研究CO2与铝合金腐蚀速率的关系。

铝合金在服役过程中，可能经受海洋大气、干热沙漠、寒冷低温、高原低气压等多种复杂环境[17]，其大气腐蚀规律具有区域性差异。大气环境中，相对湿度越大，金属表面越易形成薄液膜，且存在时间也越长，腐蚀速率随着增加，风速影响污染介质扩散程度，直接影响铝的耐蚀性。将时间作为直接效应，考量温度、相对湿度、风速等因素作为不同环境间差距进行研究。

1）时间对铝合金大气腐蚀的直接效应。铝合金在大气暴露中腐蚀属于电化学腐蚀，其腐蚀速率逐渐降低。因为金属表面随时间逐渐形成锈层，锈层厚度增加，使得锈层电阻增大，致使锈层更加致密，而活性阳极面积变小，加剧氧的渗入难度，从而减弱锈层阴极去极化作用，促进阳极极化。除特殊环境外，整体上来看，金属材料的大气腐蚀速度逐渐减慢[23]。

2）温度对铝合金大气腐蚀的影响作用。温度直接影响化学腐蚀的反应速率，统计表明，控制其他环境条件的情况下，平均气温高或者昼夜温差比较大的地区，大气腐蚀的速率一般比较大[24]。但温度不完全和腐蚀速率呈正相关关系，不同环境下，铝合金腐蚀速率存在不同的临界值，所以温度对腐蚀普遍具有正反馈作用，但温度与其他因素耦合作用，不完全存在正相关关系。

3）相对湿度对铝合金大气腐蚀的影响作用。相对湿度指在某一温度下空气中水蒸气同温度下饱和水蒸气量的百分比，当水蒸气超过饱和出现水珠，金属表面产生由空气中的水分子凝聚生成的液膜，液膜在多数大气腐蚀起决定性作用，致使在一定范围内金属腐蚀速率与相对湿度基本呈正相关关系。大气相对湿度影响铝合金表面液膜厚度，但液膜厚度在1 μm时，腐蚀速率最大，增大或减小都将降低速率[25]。

4）日照时长对铝合金大气腐蚀的影响作用。日照时长关系金属表面液膜存续，在日照时长较大的情况下，液膜容易消失，表面浸润时间短，进而使得金属腐蚀总量降低，出现腐蚀速率减小的情况。

5）降水量对铝合金大气腐蚀的影响作用。降水量是体现降雨的最直观因素，降水量与空气相对湿度基本呈正相关关系，降水量越大，浸润时间越长，腐蚀速率越大。另外，降水的冲刷作用具有争议，一方面，降雨的冲刷会破坏对基体具有保护作用的腐蚀产物，从而加速金属的腐蚀；另一方面，降雨也会冲刷掉金属表面的污染物或者灰尘等沉积物，达到减缓腐蚀的效果，最终加速腐蚀还是减缓腐蚀尚未定论[23]。

6）风速对铝合金大气腐蚀的影响作用。风速与空气中各类分子、离子运动速率休戚相关，风速基本与腐蚀速率呈正相关性。风速越大，水蒸气与铝合金接触越充分，离子运动更剧烈，导致腐蚀加剧。

影响铝合金应力腐蚀行为的环境因素主要有相对湿度、环境温度、腐蚀介质、溶液溶氧量及pH值等[25]。本文采用通用环境因素，初步探究多层线性模型对铝合金大气腐蚀规律的适用性，只对气象因子作研究，暂不对大气污染介质进行分析。

3 变量定义

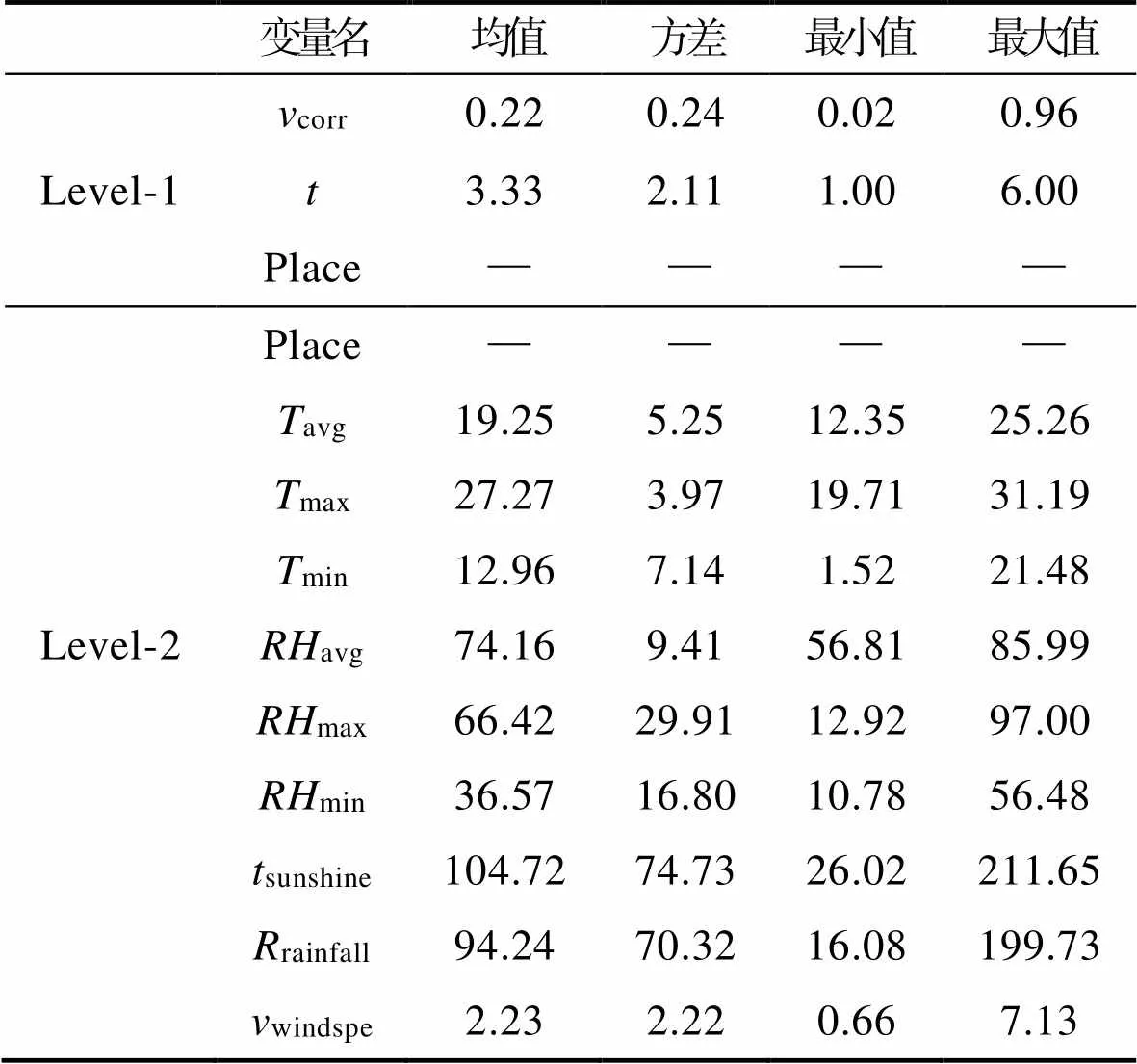
在铝合金大气腐蚀环境试验原始数据中，包含材料类别、材料品种、材料牌号、热处理状态等基础信息，试验站名称、试验站编号等试验站信息，投样日期、试验时间等时序数据，拉伸性能如抗拉强度、屈服强度、断后伸长率等金属力学性能数据，腐蚀速率等二次计算数据，以评估铝合金的大气腐蚀程度。通过查询对应年份的气象因子数据，得到不同地区的环境因素数据，作为模型参数。部分原始数据见表1。

两层线性模型的原始数据统计见表2。第一层为铝合金大气腐蚀环境效应数据，corr指铝合金腐蚀速率，作为因变量，指环境试验放置时间，Place指试验地点，无均值方差，作为与第二层的关联字段。第二层通过环境因素数据表征不同环境特征，含avg（平均温度）、max（最高温度）、min（最低温度）、avg（平均相对湿度）、max（最大相对湿度）、min（最小相对湿度）、sunshine（日照时长）、rainfall（降水量）、windspe（平均风速）等。

表1 某型铝合金大气腐蚀原始数据

Tab.1 Original data of atmospheric corrosion of a certain type of aluminum alloy

表2 两层线性模型原始数据统计

Tab.2 Original data statistics of two-layer linear model

4 模型计算与实证分析

4.1 零模型

为论证不同环境下铝合金的大气腐蚀是否存在显著差异，首先对总方差进行分解，将行为差异分解为不同环境效应数据的组间方差和组内方差2部分[26]，观察二者占比。

第一层方程：

第二层方程：

(4)

式中：Y代表环境因素第组数据；0j为第一层截距，代表环境的随机效应；r为第一层的残差，代表个体层次的随机效果[27]；00为第二层的截距，代表环境因素层面固定效应；0j为环境的随机效应，衡量不同环境之间的变异量。

表3 零模型混合效应评估结果

Tab.3 Evaluation result of mixed effects of zero model

表4 零模型随机效应评估结果

4.2 随机系数回归模型

在零模型的基础上，为进一步探究铝合金大气腐蚀是否具有类线性规律，探究不同环境因素产生的性能变化规律是否存在差异。随机系数回归模型通过在第一层方程中加入时间参数项，假定预测退化性能在不同环境间的影响恒定，分析不同环境因素变量对铝合金大气腐蚀的规律。建立随机系数的回归模型，见式（5）—（7）。

第一层方程：

第二层方程：

(7)

式中：除零模型基本参数外，t代表环境因素第组数据测量时间，铝合金大气腐蚀性能退化数据随时间变化；1j为时间参数的斜率，代表环境时间参数的随机效应。第二层0j定义环境的随机效应，1j定义时间的偏回归系数。分析结果见表5和表6。

由分析结果可知，时间与腐蚀速率呈负相关关系，符合铝合金腐蚀机理。铝合金在大气腐蚀中首先生成氧化膜，随后腐蚀速率减缓，而此处时间以a为单位，在1 a即第一个试验数据处取得峰值，随后降低。在随机效应中，0j代表不同环境的随机效应，其=0.049<0.05，接受假设，证明不同环境对腐蚀速率的影响较大。1j对应值超限，证明时间的随机效应对腐蚀速率的变化缺乏可解释性，变异不显著，在模型构筑中将其固定为固定参数。因此，需要对随机系数回归模型进行调整。

表5 随机系数回归模型混合效应评估结果

Tab.5 Evaluation result of mixed effects of random coefficient regression model

表6 随机系数回归模型随机效应评估结果

Tab.6 Evaluation result of random effects of random coefficient regression model

第一层方程：

第二层方程：

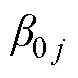
表7 随机系数回归模型调整后混合效应评估结果

Tab.7 Evaluation result of mixed effects of random coefficient regression model after adjustment

表8 随机系数回归模型调整后随机效应评估结果

Tab.8 Evaluation result of random effects of random coefficient regression model after adjustment

4.3 完整模型

基于零模型与随机系数回归模型的研究，进一步推进到完整模型，其理想状态为囊括所有因素，并纳入非线性，理想完整模型见式（11）—（13）。

第一层方程：

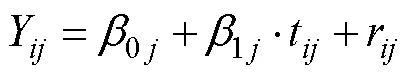
第二层方程：

(12)

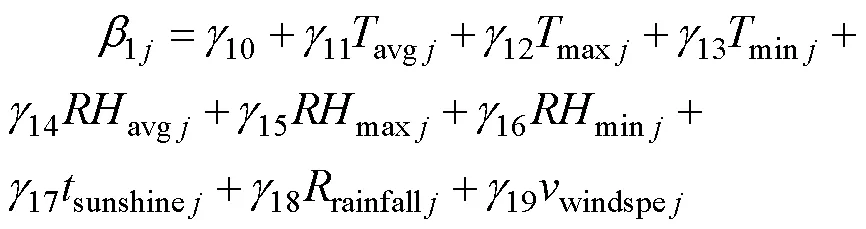
其中，avgj、maxj等代表环境的各类环境因素数据（参数含义见2.2）。0j加入环境因素数据有效衡量了不同环境的差异性，1j即时间斜率加入环境因素数据。从机理考虑，在自然大气腐蚀中，受环境因素的积累影响，从数理统计考虑，加入非线性使模型更加完整。

理想完整模型中有22个待定参数，无法使用本数据集中小样本数据进行计算统计、假设检验，且某些参数具有一定的共线性，所以需要减少参数量，剔除权重较小、变异较不显著的参数。采用单参数检验的方法考察所有参数的显著性[28]，最终确认第二层方程变更为：

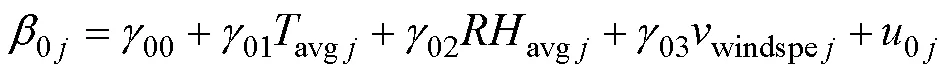
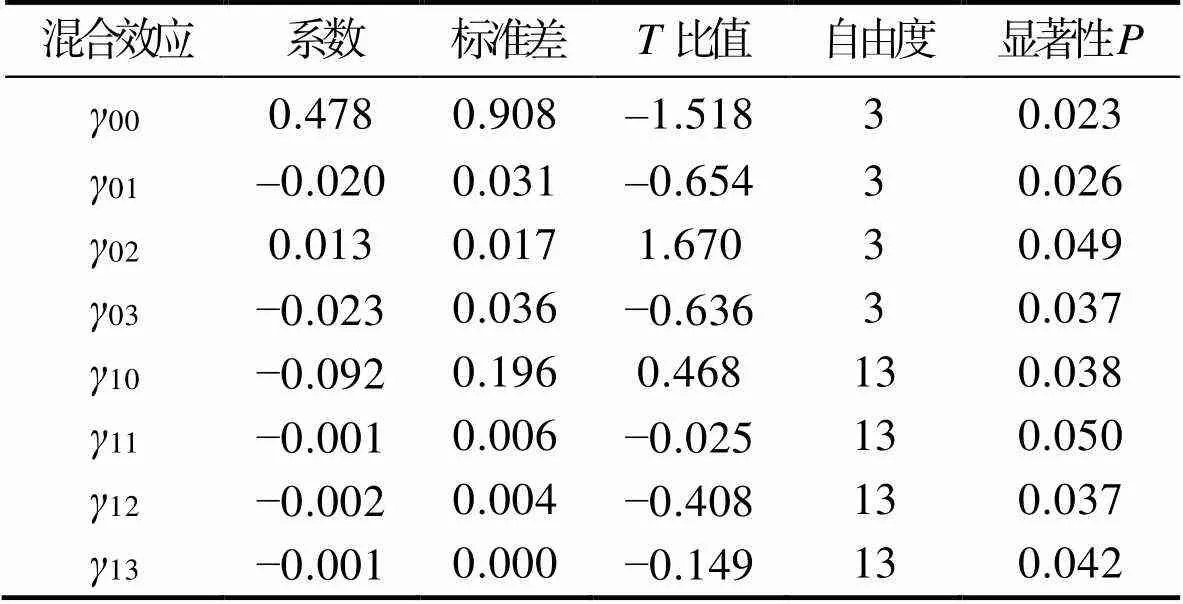
分析结果见表9和表10。为便于后续使用，此处分析未做标准化、归一化，导致某些参数权重具有差异，如windspe通常为个位级，avg为十位级，虽然对应的固定系数01与03系数值差异不大，但数值结果证明温度权重高于风速权重。

表9 完整模型混合效应评估结果

Tab.9 Evaluation results of mixed effects of the complete model

表10 完整模型随机效应评估结果

Tab.10 Evaluation results of random effects of the complete model

由固定效应分析结果可知，0j代表不同环境的环境因素的固定效应，其受平均温度和风速的正向激励，受相对湿度的反向激励。其可能原因是，一部分是温湿度一定程度耦合，在联合计算时相对湿度系数体现为正值；另一部分是因为数据存在一定误差，数据体量较小，放大了该效应。1j代表时间的截距，温度、湿度、降水越大，铝合金随时间流逝，腐蚀速率下降得越快。说明在腐蚀相对活跃的地区，腐蚀历程在前期进行得更快速，在后期减缓。对第一层方程加以分析，在所有参数为0的情况下，此型号铝合金初始腐蚀率约为0.478 μm/a；对第二层方程加以分析，在所有参数为0的情况下，腐蚀速率下降为0.092 μm/a。

从随机效应结果可知，方差为0.151，在腐蚀速率均值为0.22 μm/a的情况下方差较大，说明仍存在显著差异，表明模型可进一步优化，提升解释性。对比随机系数回归模型方差为0.17，完整模型方差得到一定程度下降，下降比例为11.17%，表明环境因素参数解释初始情况11.17%的方差。

4.4 模型评估

为考察基于多层线性模型的铝合金大气腐蚀预测能力，通用做法为使用第1、3年的数据进行多层线性模型训练，使用第6年的数据进行评估分析，检验预测数据与实际数据的差异性。考虑到数据量较小，且第6年数据相较于第1、3年数据本身波动较大，所以采用随机取某2年数据为训练集，剩下1年数据作为验证集，进行交叉验证，采用典型回归评价指标[29]——均方差（MSE）进行回归差异评估，取10次结果的MSE均值作为评估结果，部分结果数据见表11。

表11 基于不同模型的预测数据比对

Tab.11 Comparison of prediction data based on different models

为合理评估模型，将线性回归与多层线性模型加以比较，直观评估多层线性模型提升效果。同时，铝合金腐蚀从腐蚀动力学层面常用幂函数回归进行预测。如苏霄[30]采用幂函数回归对质量损失与时间规律进行分析考评，所以使用幂函数回归与多层线性模型进行对比。

实际–预测数据的关系如图1所示。若数据完全落在=这条分界线上，说明预测数据与实际数据完全一致，但实际预测结果均有偏差，线性回归甚至存在小于0这种不合理数据。由图1可直观看出，多层线性模型的预测结果更贴近实际结果，幂函数回归次之，线性回归偏差最大，计算得到HLM、幂函数回归、线性回归模型的MSE分别为0.001 3、0.005 5、0.031 6，说明多层线性模型预测得到的误差最小，线性回归误差最大。由于数据均在[0, 1]，所以MSE结果均较小，但不代表线性回归的预测结果较好。

图1 实际–预测数据关系

因此，采用多层线性模型进行铝合金大气腐蚀规律预测能够有效提升预测精度，得到相较线性回归、幂函数回归更科学合理的预测结果。结合算法模型可知，多层线性模型考虑了环境内在因素对大气腐蚀的影响，考虑了不同层次的随机误差和变量信息，提供标准误差估计，利用多层线性模型能进一步分析大气腐蚀影响因素。综上所述，多层线性模型更适应铝合金在不同区域的大气腐蚀规律研究。

同时，由于数据存在误差，小样本误差对结果的影响更大，导致假设检验结果存在显著性一般或由于偏差导致变量不显著的情况。后续应加强试验，增加数据量，加强数据质量，加入污染介质数据，构建更准确、更具代表性的多层线性模型，并增强机理研究，通过Arrhenius公式将非线性关系映射到线性域等手段作数据预处理，构建更贴合腐蚀机理的多层线性模型。

5 结论

1）以某型号铝合金在不同地域环境试验为对象，建立多层线性模型，分析铝合金的大气腐蚀规律，具有一定普适性。

2）多层线性模型有效结合铝合金腐蚀数据区域差异性特征，利用“组内同质，组间异质”的数据特性，提升了数据分析的针对性，提升了铝合金大气腐蚀预测模型精度。多层线性模型以线性和正态分布作为基础，充分利用统计信息，在一定置信区间内可信，等价于近似解，腐蚀模型具有实用价值。

[1] 王慧婷, 史娜, 刘章, 等. 6xxx系铝合金表面腐蚀及其防腐的研究现状[J]. 表面技术, 2018, 47(1): 160-167. WANG Hui-ting, SHI Na, LIU Zhang, et al. Surface Corrosion and Corrosion Prevention of 6xxx-Series Aluminium Alloy[J]. Surface Technology, 2018, 47(1): 160-167.

[2] 李佳航, 车欣, 蒋学禹, 等. 不同温度环境下Al-7Zn- 2.5Mg-2.0Cu-0.1Zr-0.2Sc合金的力学行为研究[J]. 精密成形工程, 2022, 14(8): 140-147. LI Jia-hang, CHE Xin, JIANG Xue-yu, et al. Mechanical Behavior of Al-7Zn-2.5Mg-2.0Cu-0.1Zr-0.2Sc Alloy at Different Temperature[J]. Journal of Netshape Forming Engineering, 2022, 14(8): 140-147.

[3] 王沙沙, 杨浪, 黄运华, 等. 硼硫酸阳极氧化6061铝合金在不同大气环境中的初期腐蚀行为研究[J]. 材料研究学报, 2017, 31(1): 49-56. WANG Sha-sha, YANG Lang, HUANG Yun-hua, et al. Initial Corrosion Behavior in Different Atmospheric Environments of 6061 Al Alloy Anodized in Boron-Sulfuric Acid Solution[J]. Chinese Journal of Materials Research, 2017, 31(1): 49-56.

[4] 陶健全, 王修涛, 陈喜栋, 等. 铸造铝合金半连续铸棒组织与性能均匀性研究[J]. 精密成形工程, 2022, 14(8): 155-159. TAO Jian-quan, WANG Xiu-tao, CHEN Xi-dong, et al. Mechanical and Microstructural Homogeneity of Semi-Continuous Casting Aluminum Alloy Bars[J]. Journal of Netshape Forming Engineering, 2022, 14(8): 155-159.

[5] 钟勇, 苏艳, 罗来正, 等. 四种典型大气环境下7B50铝合金的腐蚀行为研究[J]. 装备环境工程, 2021, 18(11): 143-150. ZHONG Yong, SU Yan, LUO Lai-zheng, et al. Corrosion Behavior of 7B50 Aluminum Alloy in Four Typical Atmospheric Environments[J]. Equipment Environmental Engineering, 2021, 18(11): 143-150.

[6] 汤化伟, 邓云发, 钱帅豪, 等. 2219和2195铝合金焊接接头的腐蚀行为差异研究[J]. 精密成形工程, 2022, 14(8): 111-117. TANG Hua-wei, DENG Yun-fa, QIAN Shuai-hao, et al. Difference of Corrosion Behavior between 2219 and 2195 Aluminum Alloy Welded Joints[J]. Journal of Netshape Forming Engineering, 2022, 14(8): 111-117.

[7] 侯悦, 田原, 赵志鹏, 等. 海洋工程用铝合金的腐蚀与防护研究进展[J]. 表面技术, 2022, 51(5): 1-14. HOU Yue, TIAN Yuan, ZHAO Zhi-peng, et al. Corrosion and Protection of Aluminum Alloy for Marine Engineeri­ng[J]. Surface Technology, 2022, 51(5): 1-14.

[8] 杨博均, 魏木孟, 邓玉, 等. 铝及铝合金在自然水环境中的腐蚀行为对比研究[J]. 装备环境工程, 2022, 19(5): 106-116. YANG Bo-jun, WEI Mu-meng, DENG Yu, et al. Comp­arative Study on Corrosion Behavior of Aluminum and Aluminum Alloy in Natural Water Environment[J]. Equipment Environmental Engineering, 2022, 19(5): 106-116.

[9] 曹楚南. 中国材料的自然环境腐蚀[M]. 北京: 化学工业出版社, 2005.CAO Chu-nan. Natural Environment Corrosion of China Materials[M]. Beijing: Chemical Industry Press, 2005.

[10] SADOWSKI L. Non-Destructive Investigation of Corrosion Current Density in Steel Reinforced Concrete by Artificial Neural Networks[J]. Archives of Civil and Mechanical Engineering, 2013, 13(1): 104-111.

[11] 杨瑞成, 王彬, 张天云. 基于MATLAB的混沌时间序列算法对材料腐蚀行为的预测[J]. 兰州理工大学学报, 2009, 35(5): 5-8. YANG Rui-cheng, WANG Bin, ZHANG Tian-yun. Forecast of Material Corrosion Behavior by Means of MATLAB-Based Algorithm of Chaos Time Series[J]. Journal of Lanzhou University of Technology, 2009, 35(5): 5-8.

[12] LINDLEY D V, SMITH A F M. Bayes Estimates for the Linear Model[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1972, 34(1): 1-18.

[13] 王志军, 张豫徽, 季彦婕, 等. 基于多层线性模型的公共自行车接驳公交换乘量影响因素分析[J]. 交通运输工程与信息学报, 2022, 20(3): 81-88. WANG Zhi-jun, ZHANG Yu-hui, JI Yan-jie, et al. Analysis of the Influencing Factors of Public-Bicycle- Connecting Regular Bus Transfer Volume Based on Multilevel Linear Model[J]. Journal of Transportation Engineering and Information, 2022, 20(3): 81-88.

[14] 杨凌燕, 郭建鹏, 史秋衡. 我国大学生课堂体验及其影响因素的多层线性模型分析[J]. 复旦教育论坛, 2013, 11(6): 45-51. YANG Ling-yan, GUO Jian-peng, SHI Qiu-heng. An HLM Analysis of Chinese University Students’ Course Experience and Its Influencing Factors[J]. Fudan Education Forum, 2013, 11(6): 45-51.

[15] 唐凯铃, 陈铭聪, 温雪莲. 我国城市居民二手房购买意愿的影响因素——基于多层线性模型的实证分析[J]. 调研世界, 2021(5): 30-37. TANG Kai-ling, CHEN Ming-cong, WEN Xue-lian. Infl­uencing Factors of Second Hand Housing Purchase Intention of Urban Residents in China—Empirical Analysis Based on Hierarchical Linear Model[J]. The World of Survey and Research, 2021(5): 30-37.

[16] 耿晓梦, 喻国明. 数字鸿沟的新样态考察——基于多层线性模型的我国居民移动互联网使用沟研究[J]. 新闻界, 2020(11): 50-61. GENG Xiao-meng, YU Guo-ming. Ongoing Digital Ineq­uality: Research on the Difference of Mobile Internet Usage of Chinese Residents Based on Hierarchical Linear Modeling[J]. Journalism and Mass Communication Monthly, 2020(11): 50-61.

[17] 罗来正, 肖勇, 苏艳, 等. 7050高强铝合金在我国四种典型大气环境下腐蚀行为研究[J]. 装备环境工程, 2015, 12(4): 49-53. LUO Lai-zheng, XIAO Yong, SU Yan, et al. Corrosion Behavior of 7050 High-Strength Aluminum Alloy in Four Typical Atmospheric Environments in China[J]. Equipm­ent Environmental Engineering, 2015, 12(4): 49-53.

[18] 赵全成, 罗来正, 黎小锋, 等. 两种典型大气环境下7A85铝合金的腐蚀行为研究[J]. 装备环境工程, 2020, 17(7): 70-75. ZHAO Quan-cheng, LUO Lai-zheng, LI Xiao-feng, et al. Corrosion Behavior of 7A85 Aluminum Alloy in Two Typical Atmospheric Environments[J]. Equipment Envir­onmental Engineering, 2020, 17(7): 70-75.

[19] 崔腾飞, 刘道新, 徐星辰, 等. 高强度铝合金典型沿海地区腐蚀行为加速试验方法研究[J]. 装备环境工程, 2020, 17(5): 33-39. CUI Teng-fei, LIU Dao-xin, XU Xing-chen, et al. Accele­rated Test Method for High Strength Aluminum Alloy in Typical Coastal Area[J]. Equipment Environmental Eng­ineering, 2020, 17(5): 33-39.

[20] ARIZMENDI-SALGADO V A. Effect of Heat Treatment on the Corrosion Behavior of Welded 7075 T6 Aluminum Alloy without Filler Material[J]. International Journal of Electrochemical Science, 2019: 8243-8255.

[21] MELCHERS R E. Bi-Modal Trend in the Long-Term Corrosion of Aluminium Alloys[J]. Corrosion Science, 2014, 82: 239-247.

[22] VINCKEN J P, HENG L, DE GROOT A, et al. Saponins, Classification and Occurrence in the Plant Kingdom[J]. Phytochemistry, 2007, 68(3): 275-297.

[23] 王秀静. 金属材料大气环境早期腐蚀行为及锈层演化机制研究[D]. 北京: 机械科学研究总院, 2013. WANG Xiu-jing. Research on the Behaviors and Mecha­n­ism of the Rust Layer Evolution of the Early Stages of Atmospheric Corrosion for Metals[D]. Beijing: China Academy of Machinery Science and Technology, 2013.

[24] 柳鑫龙, 朱晓明, 安江峰, 等. 聚碳酸酯老化研究进展[J]. 高分子通报, 2014(1): 72-75. LIU Xin-long, ZHU Xiao-ming, AN Jiang-feng, et al. Polycarbonate Ageing Research Progress[J]. Polymer Bulletin, 2014(1): 72-75.

[25] 赵鹏, 苏艳. 高强铝合金应力腐蚀开裂研究进展[J]. 装备环境工程, 2016, 13(1): 130-138. ZHAO Peng, SU Yan. Research Progress in Stress Corro­s­ion Cracking of High-Strength Aluminum Alloy[J]. Equ­i­pment Environmental Engineering, 2016, 13(1): 130-138.

[26] 刘朝, 王赛君, 马超群, 等. 基于多层线性模型的情绪劳动、情绪状态和工作退缩行为关系研究[J]. 管理学报, 2013, 10(4): 545-551. LIU Zhao, WANG Sai-jun, MA Chao-qun, et al. Emotional Labor, Affective States and Work Withdrawal: Test of Hierarchical Linear[J]. Chinese Journal of Management, 2013, 10(4): 545-551.

[27] 孙秋莹. 个体因素、学校因素对内高班学生数学学业成绩影响的多层线性模型分析[D]. 北京: 中央民族大学, 2018. SUN Qiu-ying. Multi-Level Linear Model Analysis of the Influence of Individual Factors and School Factors on in the High Class Students' Mathematics Academic Performance[D]. Beijing: Central University for Nationalities, 2018.

[28] NELDER J A, LONGFORD N T. Random Coefficient Models[J]. Journal of the Royal Statistical Society Series A (Statistics in Society), 1994, 157(3): 507.

[29] 王振杰, 姚吉利. 广义测量平差分类[J]. 淄博学院学报(自然科学与工程版), 2001(1): 62-64. WANG Zhen-jie, YAO Ji-li. The Classification of General Surveying Adjustment[J]. Journal of Zibo University, 2001(1): 62-64.

[30] 苏霄. 典型铝合金在模拟海洋大气环境中腐蚀规律研究[D]. 邯郸: 河北工程大学, 2013. SU Xiao. Corrosion Behavior Study of Typical Aluminum Alloy in Simulated Marine Atmospheric Environment[D]. Handan: Hebei University of Engineering, 2013.

Atmospheric Corrosion Rule of Aluminium Alloy Based on Hierarchical Linear Model

ZHOU Jun-yan, WANG Jing-cheng, YANG Xiao-kui, WANG Jin-mei, ZHOU Kun, SHU Chang

(Southwest Institute of Technology and Engineering, Chongqing 400039, China)

The work aims to establish a more accurate atmospheric corrosion model of aluminum alloy aiming at the difference of atmospheric corrosion of aluminum alloy in different regions and the insufficient use of sample data to study the atmospheric corrosion rule of aluminum alloy in different environments. Based on hierarchical linear model, the corrosion rate model with hierarchical structure was constructed. With corrosion data of a certain type of aluminum alloy as the research object, zero model, random coefficient regression model and complete model were established step by step to explore the atmospheric corrosion rule and make prediction and evaluation. Model evaluation was performed through cross validation and HLM (MSE= 0.001 3) was superior to power function regression (MSE=0.005 5) and far superior to linear regression (MSE=0.031 6), improving the prediction accuracy. HLM could effectively decompose the total variance and enhance the interpretability of the model. The HLM combined with the regional difference characteristics of aluminum alloy corrosion data can effectively characterize the atmospheric corrosion rule, which has certain practical value.

hierarchical linear model; aluminum alloy; atmospheric corrosion; corrosion model; regional difference; interpretability

2022-06-17；

2022-09-09

ZHOU Jun-yan (1995-), Male, Master.

周俊炎, 王竟成, 杨小奎, 等. 基于多层线性模型的铝合金大气腐蚀规律研究[J]. 装备环境工程, 2023, 20(6): 147-154.

TG172.3

A

1672-9242(2023)06-0147-08

10.7643/ issn.1672-9242.2023.06.019

2022‒06‒17；

2022‒09‒09

周俊炎（1995—），男，硕士。

ZHOU Jun-yan, WANG Jing-cheng, YANG Xiao-kui, et al.Atmospheric Corrosion Rule of Aluminium Alloy Based on Hierarchical Linear Model[J]. Equipment Environmental Engineering, 2023, 20(6): 147-154.

责任编辑：刘世忠