基于改进的邻域搜索算法对立库货位分配优化的研究

王毅，王浩，李翀，郭荣坤，杨媛媛，杨华

（1 国网电力河北省分公司， 石家庄 050000； 2 武汉轻工大学 数学与计算机科学学院， 武汉 430023）

自动化立体仓库具有存取自动化和操作简便等特点，符合当前数字化技术发展需求［1］.目前，在仓库操作智能化、无人化的立库货位分配应用研究中，已经产生了大量研究成果［2］.越来越多企业采用数字孪生技术，利用该技术可以实时映射出物理实体的真实状态［3］，构建虚拟立库，对立库运行情况进行实时监控.本文研究的主要内容为：在立库货位调动前得出货位分配方案预案，将方案预案提供给堆垛机进行调度，完成货位优化分配.

自动化立库研究中，货位分配效率是影响系统整体性能与工业生产效率的一个关键因素.李鹏飞等以出入库效率和货架稳定性为优化因素，建立相应的货位优化模型，设计病毒协同遗传算法对模型进行求解［4］.李敬波等从提升货品出入效率和货架稳定性与货品的摆放为优化因素建立数学模型，利用遗传算法对模型进行求解［5］.徐伟华等利用遗传算法对密集型自动化立体仓库货位进行优化［6］.刘凯文等针对入库作业操作最大完工时间与堆垛机能耗之间关系构建相应的惩罚函数，并应用于灰狼算法，实现带有截止时间约束的自动化立体仓库堆垛机能耗调度优化算法［7］.董海等从运行时间、堆垛机利用率均衡化、货架稳定性、对产品质量影响程度四个角度出发构建多目标调度优化模型，提出一种基于权值策略及非均匀概率分布的情绪化细菌觅食算法对立库进行集成优化［8］.彭小利等针对多品种智能仓库的货位分配问题，建立了考虑多规则约束的多目标智能仓库货位分配模型，提出了一种模型求解的改进遗传算法［9］.焦玉玲等以资产出入库作业时间、货架整体等效重心和关联产品间相对聚集程度为目标函数，构建了多目标货位分配优化数学模型［10］.

上述文献对自动化立体仓库货位分配的研究较为丰富，考虑了不同分配原则，设计了不同优化算法.但存在缺少分配后货位整体分布的优化，算法收敛速度较慢等不足，根据现存的问题对货位不同状态进行编码，以提高货位分配效率为目标，设计货位分配优化模型，并利用Optimizing Tabu搜索算法对模型进行求解［11］.在Tabu搜索算法中，对邻域搜索过程融入概率分配机制，提升算法的寻优能力，对比实验分析结果表明，改进后的Optimizing Tabu搜索算法在保证最优解的前提下能够显著提升算法的收敛速度.

1 立库货位分配优化问题

自动化立体仓库［12］包括高层货架、堆垛机、传送带等.资产以托盘为单位存储在高层货架，传送带连接工作区与仓储区，输送需装卸的资产；资产的上架存储与分拣，均由堆垛机完成，堆垛机在收到指令后，对资产进行操作.

为便于问题研究，进行如下设定：（1）立库每排货架仅一个资产入口，资产出口与资产检测出入口；（2）货位只存储同一种商品，其数量、体积有限；（3）不考虑传送带与堆垛机交接时间以及取、放资产操作时间；（4）资产存入货架为入库，资产从货架的出口运出为出库.

2 货位优选模型构建与算法设计

2.1 问题模型构建

模型所涉及的参数及其定义如表1所示.

表1 模型参数定义Tab.1 Definition of model parameters

（1） 货位状态随着堆垛机对资产的不同作用而不断转变，转变规则为：R→S；S→R；H→C；C→H.即原本是入库的货位，在资产进入该货位后，货位变为送检货位，该资产的下一步操作为送检操作，完成送检操作即将资产送至检测位置，货位又变为入库货位等待资产送入；原本是接受检定完成资产回库的货位，在资产进入该货位后，货位变为出库货位，该资产的下一步操作为出库操作，完成出库操作即将资产送至出货口位置，货位又变为检定完成资产回库的货位等待资产送入.（本文将立库中的每排货架分上下两个部分，上层货位为入库与送检货位，下层为检定完回库与出库.每一层货位的转换是独立不影响资产的流动.当上层的送检货位将资产送出，会被下层的回库货位接受）.

堆垛机可以同时沿水平和竖直方向移动，每次堆垛机移动的时间为堆垛机水平方向的时间与竖直方向移动的时间的最大值，且不同状态的货位使得堆垛机移动的最终位置不同，每种操作分别是：1）入库操作：堆垛机当前位置→入口→指定货位；2）送检操作：堆垛机当前位置→指定货位→检测入口；3）回库操作：堆垛机当前位置→检测出口→指定货位；4）出库操作：堆垛机当前位置→指定货位→出库位置.

设（ms，ms）为堆垛机当前坐标，（ne，ne）为堆垛机目标位置坐标.Ts→e为堆垛机当前位置到目标位置的时间Lx，Ly，分别是货架中货位水平与竖直的距离（ms，ms）∈｛（xstacker，ystacker），（xenter，yenter），（xexport，yexport），（xtest，ytest）｝，（ne，ne）∈｛（xi，yi）｝；

堆垛机每次移动的时间如式（1）：

完成入库，送检，回库，出库操作的时间分别如式（2）、式（3）、式（4）、式（5）所示，Dstaker为堆垛机当前位置.

（2） 自动化立体仓库中有多台堆垛机并行工作，降低所有堆垛机的最大工作时间作为优化目标（j为每台堆垛机的序号）：

（3） 整体上也要降低所有堆垛机工作的时间总和：

（4） 根据（6）（7）目标分析，优化立库工作主要任务是减少立库任务的完成时间，以此为目标，将降低所有堆垛机工作的时间总和作为优化目标的一定约束.本文取T1Ttotal的比例为1000∶1（n取1000，为了将T1作为第一优化目标）.

（5） 约束条件：

2.2 Tabu搜索算法描述

Tabu搜索算法［13］通过对人类搜索信息的记忆特征进行模拟，能够有效降低算法陷入局部最优的可能性.将Optimizing Tabu搜索算法流程与原算法相同，如图1所示.

图1 Tabu搜索算法流程图Fig.1 Tabu search flow chart

Tabu搜索算法的步骤如下：

（1） 设计算法的初始参数并随机产生相应的初始解，将禁忌表置为空；

（2） 判断产生解是否满足算法终止条件？如果满足，算法运行结束否则执行一下步骤；

（3） 对当前解进行邻域搜索产生邻域解，在新产生的邻域解中确定候选解；

（4） 判断确定候选解是否满足特赦要求？满足则使用候选解替换当前解成为新的当前解，并将候选解写入禁忌表中执行步骤（2）；否则执行下列步骤；

（5） 判断候选解是否处于禁忌状态，在选择候选解时选择处于非禁忌状态的最优解作为新的当前解，并且将新的当前解更新进入禁忌表中；

（6） 执行步骤（2）.

2.3 Optimizing Tabu搜索算法的求解

利用传统的Tabu搜索算法解决立库中货位选择的问题，搜索的最终结果在一定程度上依赖于初始解的选取.虽然Tabu搜索算法的特性在一定程度上可以避免陷入局部最优的情况［14］，但是Tabu搜索算法在执行时，需要迭代次数足够充分才可以达到最优，因此会耗用大量时间，本文针对此问题，在邻域搜索过程中对不同的货位设置不同的搜索概率值.对能使解更优的货位给予一个大的搜索概率，反之则给予一个相对较小的搜索概率值，从而在整体上提高了邻域搜索过程中货位选择的效率，显著地提升了算法的寻优性能.

2.3.1 初始货位分布以及解的表达方式

每排货架上初始货位分布遵循如下准则：本文立库12排货架每排货架有26层，1-13层为R状态与S状态；14-26层为H状态与C状态.本文初始货位分布采用随机策略，1-13层中每个货位分配给R或S的概率均为50%，14-26层同理.这样分配可以使每种货位均有足够的数量在后续的仿真中能够表现出一定规律.货位状态有四种，形态分为两种：满货位（有资产存放的货位S，C两种状态）与空货位（没有资产存放的货位R，H两种状态）.该类货位都具有一个入库的时间标签，本文中的时间标签，时间标签为1-30越少入库时间越靠前，且生成初始货位分布时对该类货位随机生成一个入库时间标签.

根据本文限定场景的情况，货位的选择包括已经被选择的货位以及符合条件但是未被选中的货位，因此算法邻域搜索过程中需要对这两部分进行搜索得出最优解.

本文初始解包含两方面，第一方面是选择了哪些货位，以及货位选择的分布情况，第二方面是货位的顺序.货位的顺序指堆垛机操作资产的先后顺序，确定立库工作的时间，根据实时情况的货位选择的初始解遵循如下准则：R与H型货位，随机在该类型货位中选择.S与C型货位根据入库时间的先后排序，选择时间标签小的货位.

2.3.2 结合线性概率分配机制的邻域搜索过程

一个合理的邻域搜索方式有助于算法快速地搜索得到更优的解［13］，邻域搜索也是整个Tabu搜索算法过程中最为重要的部分，决定着算法的优劣性，本文针对传统邻域搜索策略做出一定改进，经过实验验证能提升搜索效率.

针对本文实际情况，将搜索分为外部搜索与内部搜索两种情况.外部搜索：将符合条件但未被选中的货位与已被选中的货位进行逐个交换，挑出货位选择的最优方案.内部搜索：在已经确定选择的货位中不断交换，在交换中寻得最优路径使运作时间达到最短，在进行外部搜索过程中给每一个货位一个搜索概率且按照不同位置进行概率分配.货位搜索概率分布遵循按货位坐标与对应的传送口位置坐标的远近进行计算，每个货位被搜索到的概率P(x，y)如下式：（xtarget， ytarge）t当前货位对应出入口位置的坐标，货架货位数量为26 × 26.

搜索概率的计算方式为，货架行列数的最大值+1减去货位坐标与目标位置横（纵）坐标差的最大值，除以货架行列数最大值，将商记为概率P(x，y)，货架行列数的最大值+1可以提高在目标位置搜索附近搜索的概率）：

2.3.3 禁忌表与禁忌对象以及候选解的确定

本文将货位的交换操作作为禁忌对象，在算法的若干次迭代中禁止交换过的货位再次进行交换.禁忌表长度：禁忌表长度是禁忌对象在不考虑特赦准则的情况下不允许被选取的最大次数，禁忌长度的选取与解决的问题和经验有关，本文选取禁忌表的长度为20，本文根据实际情况从邻域中搜索出1000个解，取最优的10个解，作为候选解集，在候选解的集合中选取最优的候选解.

2.3.4 特赦条件

在Tabu搜索算法过程中，会出现选取的候选解全部被禁忌的情况［15］，特赦条件是指当所有候选解中选择最优的解，且必须优于当前解，则可以忽略禁忌准则，解禁该候选解，并替换当前解更新禁忌表.

为了能够更进一步避免算法陷入局部最优，在候选解替换当前解时遵循如下准则（设CS为当前解，OS为候选解中准备替换CS的解）：当OS优于CS的1%时正常替换，否则对是否替换加入一个较小的概率，本文中如果OS优于CS小于1%，存在1%的可能忽略替换操作继续运行算法［16］.

3 仿真数据与实验仿真

3.1 仿真数据

本文以河北检定中心自动化立体仓库为例，立库中存在12排货架，每排货架有52列26层，六台堆垛机并行工作，每台堆垛机均固定操作指定的两排货架，堆垛机每次水平搬运两垛相同类型资产，因此根据这一特性可以将货架原本的52列货位在编码时转换成26列进行编码，编码时每个货架对应货位数量：26 × 26.堆垛机水平对应两个货架为一个整体，需要操作某种货位时根据每个堆垛机操作该类型货位状态数量的比例来进行分配，每排货架中坐标（1，1）距入货口最近；坐标（1，13）距离检测出入口最近；坐标（26，13）距离出货口最近，堆垛机速度与货位规格参数见表2.

表2 相关参数设定Tab.2 Setting of relevant parameters

使用c语言实现货位分配优化算法并进行实验仿真，已知初始货位分布，模拟设定需求下的货位分配，已知程序编码中单个堆垛机对应两排货架共1352个货位，整个立库共有8112个货位，每排货架中的编码货位为676个，对以下情况进行实验：某时刻需要对立库的货位进行分配，需要分配相同数量的四类货位数量，每类货位数量需求为720个.由于在生成初始货位时，每种类型货位生成的概率均为50%，平均每个货架每种货位的分配数量约为60个，随机选取一个货架分析相关规律.

3.2 实验结果与分析

3.2.1 对货位分配后结果的分析

通过大量的实验仿真，得出解的货位分布如图2.（从左到右依次是初始货位分布，初始解的分布，优化后解的分布，改进后优化解的分布.）

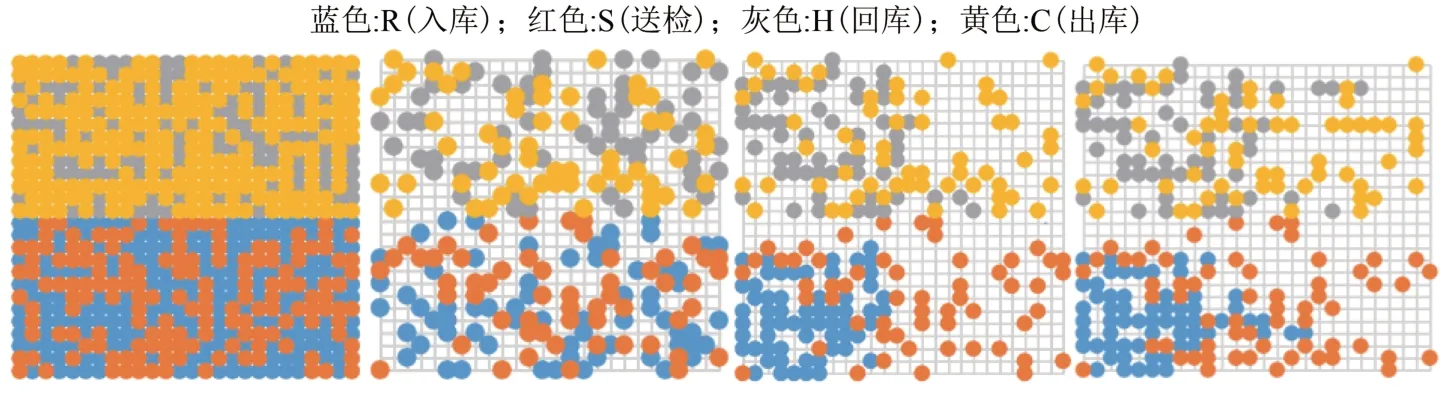
图2 货位分布Fig.2 Location distribution

经过对实验结果的分析，改进前后解在分布上的表现接近完全相同，说明两种搜索方式均可以达到相同效果，因此本文接下来将会对改进前后的搜索方式在算法中的迭代效果进行对比，以及对程序收敛性的影响进行分析.

对比初始解的分布与优化后解的分布，入库资产货位的选择整体上全部集中在入货口的位置，回库货位的选择也是整体上集中于回库口的位置，分析可知，由于这两类货位属于空货位是不受入库时间所约束，因此整体上都较为靠近与之关联的库位.

由于送检与出库货位分布优化后依然呈现得十分散乱，因此随机挑选部分入库货位与送检货位的入库时间进行分析，入库时间信息如表3所示.

表3 部分货位入库时间信息Tab.3 Storage time information of some storage locations

观察送检货位与出库货位的选择中部分散乱货位的入库时间，分布结果十分散乱，但是入库时间均十分靠前，符合算法先考虑时间，再考虑距离的原则，符合货位选取的目标且可以有效地避免货位长期在立库中堆积.

3.2.2 迭代次数与立库工作时分析

每种搜索方式的迭代次数与立库执行时间如表4所示，t1表示改进前算法的最优解，t2表示改进后算法的最优解，即公式（8）的目标函数值，该函数值是将最大工作时间与每台堆垛机工作时间的和按一定比例结合，因此实际时间会略大.

表4 迭代次数与立库工作时间表Tab.4 Number of iterations and work schedule of Warehouse Establishment

从表4得出：改进后的Tabu搜索算法与原算法相比，在迭代前期最优解优化概率明显具有优势且收敛速度也明显快于改进前，将改进后的Tabu搜索算法与原算法收敛效果进行对比如图3所示.

图3 迭代次数与时间分析图Fig.3 Analysis of iteration times and time

由图3可得：改进后的Tabu搜索算法收敛效果明显优于原算法，改进后的Tabu搜索算法可以减少迭代次数达到相同甚至更优的解，提升了算法的效率，在一定程度上减弱了Tabu搜索算法对初始解的依赖程度.

3.2.4 算法性能分析

为了对算法的性能进行分析，只研究一台堆垛机的生产流程，选取货位总数为80，四种货位选取概率相同.选取单一货架货位分布如图4.（从左到右依次是初始货位分布，初始解的分布，改进后优化解的分布.）

图4 货位分布Fig.4 Location distribution

为验证算法的优越性，计算每次货位规划的迭代次数.通过优化货位的分配，优化前后结果如表5所示，time1，time2为程序运行时间单位均为/s.

表5 收敛次数与工作时间表Tab.5 Convergence times and working time

由表5可得，算法在相同的收敛次数下，本文算法收敛提升接近60%.算法核心是提升搜索过程中的寻优能力，减少需要收敛的次数，且计算能控制在1 min左右，能够满足现场实时性的要求，与文献［17］中采用遗传算法进行优化相比，在优化效率上具有更加优越的表现.

4 总结

经过对实验结果的分析，本文结论如下：

（1） 结合概率机制后的Tabu搜索算法，相比传统的Tabu搜索算法，具有更快的收敛速度，能够避免传统方式陷入局部最优解的缺陷，从而提高了自动化立库中货位优化的水平.

（2） 改进Tabu搜索算法优化后，提高了自动化立体仓库货位搬运效率.能够减少资产流动过程中所消耗的时间.

综上所述，通过加入概率机制的Tabu搜索算法能够优化自动化立体仓库的货位分配，提高资产流动效率，从而减少资产的堆积，提高生产效率.