数学核心素养视阈下的初中几何“一题多解”教学探究
金木红

近年来,“核心素养”一词在数学教育研究中“独占鳌头”,成为研究热点。《义务教育数学课程标准(2022年版)》指出,数学课程要培养学生的核心素养,教会学生能用数学的眼光观察世界,能用数学的思维思考世界,能用数学的语言表达世界。对一线教师而言,就是要将日常的教学经验提取出来,以总结归纳出有效的核心素养的落地途径。
教学的根本目的是“授之以渔”,不仅要教给学生必要的基础知识,更要教给学生基本的学习方法,培养和发展学生的思维能力。初中数学教学过程中,在教育学生掌握和理解基础数学知识的同时,还要培养学生用发散性思维多角度思考问题的能力。“一题多解”训练就是启发和引导学生从不同的角度,运用不同的思路和方法以及不同的运算过程,去分析、解答同一道数学题的练习活动。一题多解是诸多解题策略的综合运用。这一教学过程中,学生的思维积极性得到充分调动,有利于开阔学生分析问题的视野和思路,有效锻炼思维的灵活性,培养和发展学生对新旧知识的迁移能力,不断促成学生初中数学核心素养的养成。在教学过程中,应积极适宜地开展“一题多解”的训练,鼓励学生运用“一题多解”力求找到最合理、最简便的解法,将数学核心素养培养有机融入。下面笔者以几个典型题目为例,通过开展“一题多解”教学,探究如何培养学生的数学思维能力和数学核心素养。
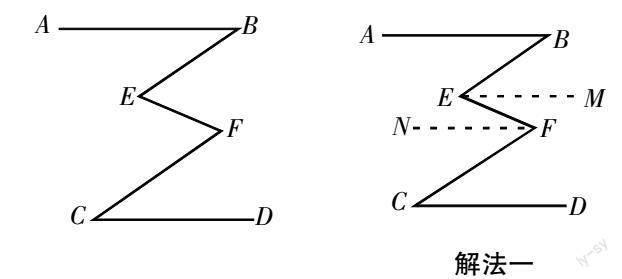
例1:如图,已知∠A=∠F,∠DBA+∠DEC=180°.
请问,BD∥CE吗?为什么?
解法一:因为∠A=∠F
所以DF∥AC
所以∠D=∠DBA
又因为∠DBA+∠DEC=180°
所以∠D+∠DEC=180°
所以BD∥CE.
解法二:因为∠A=∠F
所以DF∥AC
所以∠DEC+∠ECA=180°.
又因为∠DBA+∠DEC=180°.
所以∠ECA=∠DBA.
所以BD∥CE.
分析:本题是湘教版七年级数学下册(义务教育教科书)平行线判定第2课时例题的一个变形题目,目的在于巩固新知,检测学生对平行线判定掌握的情况。并且本题可以应用一题多解,鼓励学生开动脑筋,积极思考,培养学生的数学思维。本题难度不大,但由于七年级学生刚开始接触几何知识,所以能用两种方法严谨地写出解答过程还是有一定的挑战的。课堂上,教师要留给学生充分的时间思考,并且鼓励学生大胆尝试用不同的解法来解同一道题目,要想数学思维得到提升,必须长期坚持“一题多解,一题多练”。
本题考查平行线判定,目前学习了三种方法来判定两直线平行。解法一是利用构造同旁内角互补,判定两直线平行。解法二是利用构造同位角相等,判定两直线平行。
例2:如图,已知∠B=∠C,AB∥CD.
解法一
试判定BE与CF的位置关系,并说明理由.
解法一:BE∥CF,理由如下:
过点E作EM∥AB,过点F作FN∥CD,
所以∠B=∠BEM,∠C=∠CFN
又因为∠B=∠C
所以∠BEM=∠CFN
又因为AB∥EM,AB∥CD,FN∥CD,
所以EM∥NF
所以∠MEF=∠EFN
則∠BEM+∠MEF=∠CFN+∠EFN
即∠BEF=∠CFE
因此BE∥CF.
分析:本题仍然是考查平行线判定,但是较例1而言,难度上升了许多。题目要求证明BE∥CF,但是BE与CF之间并没有同位角、内错角、同旁内角,所以本题需要添加辅助线,这是本题需要最先突破的一个点。学生认真观察图形后能意识到这一点,但是怎样构造辅助线成了解决此题的“拦路虎”。善于思考的学生会类比例1来构造同位角、内错角或者同旁内角。解法一是大多数学生容易想到的,过拐点作平行线,构造内错角相等,从而得到两直线平行。但是此方法要用到多次平行,书写过程也比较麻烦,初学者逻辑语言不够熟练,也容易出错。考试时建议用简单、准确、快捷的方法来提高解题效率。因此,教师可以引导学生寻求更简便的方法来解答,鼓励学生积极思考,充分发挥学生的逻辑思维能力和分析能力,从而取得突破。本题对于刚刚开始接触几何学习的七年级学生来说确实有一定的难度,但是只要老师耐心引导,分解难度,给学生充分的思考空间,相信一定会有学生找出更优的解题方法。
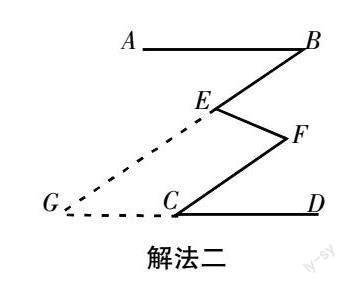
解法二:BE∥CF,理由如下:
延长BE,DC交于点G.
因为AB∥CD
所以∠B=∠G
又因为∠B=∠FCD
所以∠G=∠FCD
因此BE∥CF.
解法三:BE∥CF,理由如下:
连接BC.
因为AB∥CD
所以∠ABC=∠BCD
又因为∠ABE=∠FCD
∠EBC=∠ABC-∠ABE
∠FCB=∠BCD-∠FCD
所以∠EBC=∠FCB
因此BE∥CF.
分析:显然解法二和解法三比解法一要简单得多,巧妙地避开了二次平行的烦琐转化。学生想到这些方法,说明对平行线的性质和判定已经熟练掌握,学习达到一种更高层次。解法二是延长BE,DC交于点G.构造∠G=∠FCD,利用同位角相等,从而两直线平行。解法三是连接BC,利用AB∥CD,找到内错角∠ABC=∠DCB,再运用等量减等量差相等,得到∠EBC=∠FCB,利用内错角相等,两直线平行。两种方法都是构造角的关系,但是后面两种解法一步到位,直接找到同位角、内错角是由BE与CF两条被截线产生的,简单明了,考试肯定首选这两种解法。当然本题也还有其他解法。
解法四:BE∥CF,理由如下:
过点F作FN∥CD,延长BE交FN于点G.
因为FN∥CD
所以∠NFC=∠C
又因为AB∥CD,FN∥CD
所以AB∥FN
所以∠B=∠EGF
又因为∠B=∠C
所以∠EGF=∠NFC
因此BE∥CF.
[A][B][C][D][E][F][G][N]
解法四
解法五:BE∥CF,理由如下:
过点E作直线MN交AB与点M,交CD于点N,交FC于点G.
因为AB∥CD
所以∠BME=∠GNC
又因为∠B=∠C
所以∠MEB=180°-∠B-∠BME
∠CGN=180°-∠C-∠GNC
所以∠MEB=∠CGN
又因为∠CGN=∠EGF
所以∠MEB=∠EGF
因此BE∥CF.
[A][B][C][D][E][F][G][M][N]
解法五
分析:解法四是过点F作FN∥CD,并延长BE交FN于点G.构造内错角∠EGF=∠NFC,从而得到BE∥CF;解法五是过点E作直线MN交AB与点M,交CD于点N,交FC于点G。构造同位角∠MEB=∠EGF,从而得到BE∥CF。两种方法殊途同归,都是通过添加辅助线,构造内错角或者同位角的关系来判定两直线平行。
需要注意的是,学生刚接触初中几何,教师一定要循循善诱做好适当的引导,不能完全放手。特别是基础比较薄弱的学生,他们容易犯难,如果多次做不出来,容易灰心丧气,甚至放弃学几何。当学生能比较熟练解答几何题目后,教師也要学会适当放手,给予学生足够的时间思考,并要求他们写下解答思路,并分享给大家。还要鼓励学生大胆尝试其他的做法。长期坚持每道几何题目都争取用两种以上的方法来证明,这样学生解答几何题目的数学思维一定能培养起来,也能很好地培养数学核心素养。
以上几道例题是笔者在平时课堂教学中,所任教班级的学生主动展示的解题方法。学生们大胆地发言,严谨地叙述解答过程,甚至课后主动把题目和解答过程认真整理书写在错题本上,作为教师,笔者倍感欣慰。教学应该是以学生的动机和发展需要来展开的。教学不是一味地按照课本进行,而是教师与学生共同探讨,一起决定学习的内容和建构知识的过程,是挖掘、拓展教材深刻内涵的过程,是开发和创新课程的过程。只有这样的教学才能使教师和学生得到共同的成长。
“一题多解”运用在教学中并不是单纯地寻找多种解法,它有两个作用:一是从多个角度分析有助于挖掘问题的深层结构;二是利用一个问题来联系不同的知识点,帮助学生形成知识结构体系。在一题多解中要注意从以下几个方面培养学生的创造思维能力和数学核心素养。一要注意培养学生的发散性思维;二要注意启发学生的灵感;三要充分利用“学生渴求他们未知的、力所能及的问题”的心理,培养学生创新的兴趣(例如:田忌赛马、将军饮马、勾股定理等);四要积极鼓励学生发现问题、提出问题、讨论问题、解决问题,通过质疑、解疑,让学生具备创新思维、创新个性、创新能力。
弗里德曼《怎样学会解数学题》中强调:“解题不仅仅是为了找到答案”,他说:“应当学会这样一种对待题目的态度,即:把习题看作是精密研究的对象,而把解答题目看作是设计和发明的目标。”可见,一题多解训练,有利于学生更好地理解数学的概念、定理及其知识体系,养成从整体的角度思考问题和解决问题的习惯,形成举一反三、追根溯源的能力和敢于探索、勇于创造的精神,从而更好地把握数学学科的知识结构和本质特征,最终达到潜移默化地培养学生数学核心素养的目的。
总之,数学教学应该建立在学生兴趣的基础上。因此,数学教学应体现学生的主体参与,教师要有效引导学生发现问题、提出问题、探索并解决问题,让他们在“学中做,做中学”的过程中不断成长。在数学课堂教学中,教师应根据知识点、考点、难点、易错点精选典型题目,鼓励学生积极探索多种解法,从而激发学生内心深处的创新意识。同时,在此过程中,教师需要引导学生站在系统的高度用联系的观点看待教材各部分知识,帮助学生不断总结与反思解决问题的方法和技巧,进一步加强学生认知的开发,使学生真正领悟数学思想和方法,逐步提升数学思维,培养数学核心素养。
参考文献:
吴正宪.数堂教学策略:师生互动共同创建有效课堂[M].北京:北京师范大学出版社,2010.
(作者单位:铜仁一中初级中学)
编辑:曾彦慧

